分野（物理学）

正電荷 (赤) と負電荷 (青) を囲む電界の図。

科学において、場とはスカラー、ベクトル、スピノル、またはテンソルで表される物理量であり、空間と時間の各点で値を持ちます。^{[ 1 ] [ 2 ] [ 3 ]}スカラー場の一例としては天気図があり、地表温度は地図上の各点に番号を割り当てることで表されます。地表風速図^{[ 4 ]}は、地図上の各点に矢印を割り当て、その点での風向と速度を表すもので、ベクトル場、つまり 1 次元 (ランク 1) テンソル場の一例です。場の理論、つまり空間と時間における場の値の変化を数学的に記述したものは、物理学ではいたるところで用いられています。例えば、電場もランク1 テンソル場ですが、電気力学は時空内の各点で相互作用する 2 つのベクトル場として、または単一ランクの 2 テンソル場として定式化できます。^{[ 5 ] [ 6 ] [ 7 ]}

現代の量子場理論の枠組みでは、テスト粒子を参照しなくても、場は空間を占有し、エネルギーを含み、その存在は古典的な「真の真空」を排除します。^{[ 8 ]}このことから、物理学者は電磁場を物理的実体とみなすようになり、場の概念は現代物理学の基盤を支えるパラダイムとなりました。リチャード・ファインマンは、「電磁場が運動量とエネルギーを持つことができるという事実は、電磁場を非常に現実的なものにしています。[…] 粒子は場を作り、場は別の粒子に作用します。そして、場は粒子が持つことができるのと同じように、エネルギー量や運動量といったよく知られた特性を持ちます。」と述べています。^{[ 9 ]}実際には、ほとんどの場の強度は距離とともに減少し、最終的には検出できなくなります。例えば、ニュートンの重力理論における重力場や古典電磁気学における静電場など、多くの関連する古典場の強度は、発生源からの距離の2乗に反比例します（つまり、ガウスの法則に従います）。

場は、表現される物理量がスカラー、ベクトル、スピノル、テンソルのいずれであるかによって、それぞれスカラー場、ベクトル場、スピノル場、テンソル場に分類できます。場は、どこで定義されても一貫したテンソル特性を持ちます。つまり、ある場は、ある場所ではスカラー場、別の場所ではベクトル場になることはできません。たとえば、ニュートンの重力場はベクトル場です。時空のある点でその値を指定するには、その点における重力場ベクトルの成分である3つの数が必要です。さらに、各カテゴリ（スカラー、ベクトル、テンソル）内では、場は、数で特徴付けられるか量子演算子で特徴付けられるかによって、古典場または量子場のいずれかになります。この理論では、場の同等の表現は場の粒子、たとえばボソンです。^{[ 10 ]}

歴史

アイザック・ニュートンにとって、万有引力の法則は、質量の大きい物体の任意のペア間に働く重力の力を単純に表現したものでした。太陽系の惑星のように相互作用する多くの物体の運動を見る場合、各ペア間の力を別々に扱うと計算上すぐに不便になります。18 世紀に、これらすべての重力の記録を簡素化する新しい量が考案されました。この量、重力場は、空間の各点において小さな物体が感じる総重力加速度を与えました。これによって物理学はまったく変わりませんでした。物体にかかる重力の力を個別に計算してから合計しても、すべての寄与をまず重力場として合計してから物体に適用しても、問題はありませんでした。^{[ 11 ]}光学における光の反射と屈折は表面全体での相互作用から生じるという彼の考えは、電気力場理論の始まりと言えるでしょう。^{[ 12 ]}

場という独立した概念の発展は、19世紀に電磁気学の理論が発展したことで本格的に始まりました。初期の段階では、アンドレ＝マリー・アンペールとシャルル＝オーギュスタン・ド・クーロンは、電荷対または電流間の力を表すニュートン流の法則で対応していました。しかし、場のアプローチを採用し、これらの法則を電場と磁場の観点から表現することがはるかに自然になりました。1845年、マイケル・ファラデーは初めて「磁場」という用語を考案しました。^{[ 13 ]}そして、ケルビン卿は1851年に場の正式な定義を与えました。^{[ 14 ]}

電磁波と呼ばれるこれらの場の波が有限の速度で伝播するというジェームズ・クラーク・マクスウェルの発見により、場の独立性はより明確になった。その結果、電荷や電流に働く力は、もはや他の電荷や電流の同時刻の位置と速度だけでなく、過去の位置と速度にも依存するようになった。^{[ 11 ]}

マクスウェルは当初、独立して存在し得る基本量としての場という現代的な概念を採用しませんでした。彼は代わりに、電磁場がゴム膜の張力のように、基礎となる媒質（光伝導エーテル）の変形を表すと考えました。もしそうだとすれば、観測される電磁波の速度は、エーテルに対する観測者の速度に依存するはずです。多大な努力にもかかわらず、このような効果の実験的証拠は見つかっていませんでした。この状況は、 1905年にアルバート・アインシュタインが特殊相対性理論を導入したことで解決されました。この理論は、移動する観測者の視点の相互関係を変化させました。観測者は、マクスウェルの理論における電磁波の速度がすべての観測者にとって同一となるように、相互関係を持つようになりました。背景媒質の必要性を排除することで、この発展は物理学者に場を真に独立した実体として考え始める道を開いたのです。^{[ 11 ]}

1920年代後半、量子力学の新しい法則が初めて電磁場に適用された。1927年、ポール・ディラックは量子場を用いて、原子がより低い量子状態へ崩壊すると、電磁場の量子である光子が自然放出される仕組みをうまく説明した。その後すぐに（パスクアル・ジョーダン、ユージン・ウィグナー、ヴェルナー・ハイゼンベルク、ヴォルフガング・パウリらの研究に続いて） 、電子や陽子を含むすべての粒子は、何らかの量子場の量子として理解できるという認識が広まり、場は自然界で最も基本的な物体の地位にまで高められた。^{[ 11 ]}とはいえ、ジョン・ホイーラーとリチャード・ファインマンはニュートンの遠隔作用という前場概念を真剣に検討した（ただし、一般相対性理論や量子電気力学の研究で場の概念が現在も有用であるため、彼らはそれを棚上げにした）。

古典分野

古典場の例はいくつかあります。古典場の理論は、量子特性が生じない領域では依然として有用であり、活発な研究分野となり得ます。材料の弾性、流体力学、マクスウェル方程式などがその好例です。

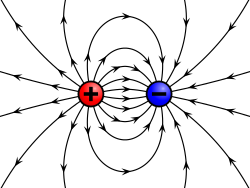
最も単純な物理場の一つにベクトル力場があります。歴史的に、場が初めて真剣に考慮されたのは、電場を記述する際にファラデーの力線が用いられた時でした。重力場も同様に記述されました。

ニュートンの重力

古典的な重力では、質量は引力重力場gの源です。

重力を記述する古典的な場の理論はニュートンの重力であり、重力の力を 2 つの質量間の相互作用として記述します。

質量Mを持つ任意の物体は、他の質量を持つ物体への影響を表す重力場gと関連している。空間内の点rにおけるMの重力場は、 rに位置する小さな、あるいは無視できる試験質量mにMが及ぼす力Fと試験質量自体の比に対応する。 ^{[ 15 ]}

${\displaystyle \mathbf {g} (\mathbf {r} )={\frac {\mathbf {F} (\mathbf {r} )}{m}}.}$

m がMよりもはるかに小さいことを規定すると、mの存在がMの動作に無視できる影響しか与えないことが保証されます。

ニュートンの万有引力の法則によれば、F ( r ) は次のように与えられる^{[ 15 ]}

${\displaystyle \mathbf {F} (\mathbf {r} )=-{\frac {GMm}{r^{2}}}{\hat {\mathbf {r} }},}$

ここで、 Mとmを結ぶ線に沿ってMからmを指す単位ベクトルである。したがって、 Mの重力場は^{[ 15 ]}である。${\displaystyle {\hat {\mathbf {r} }}}$

${\displaystyle \mathbf {g} (\mathbf {r} )={\frac {\mathbf {F} (\mathbf {r} )}{m}}=-{\frac {GM}{r^{2}}}{\hat {\mathbf {r} }}。$

慣性質量と重力質量が前例のない精度で等しいという実験的観察は、重力場の強度が粒子が受ける加速度と一致するという同一性につながります。これが等価原理の出発点であり、一般相対性理論へとつながります。

重力Fは保存力であるため、重力場g はスカラー関数の勾配、重力ポテンシャルΦ( r ) で書き直すことができます。

${\displaystyle \mathbf {g} (\mathbf {r} )=-\nabla \Phi (\mathbf {r} )。}$

電磁気

マイケル・ファラデーは、磁気の研究中に、物理量としての場の重要性を初めて認識しました。彼は、電場と磁場が粒子の運動を規定する力場であるだけでなく、エネルギーを運ぶため、独立した物理的実体を持っていることに気づきました。

これらの考えは最終的に、ジェームズ・クラーク・マクスウェルによる電磁場の方程式の導入を伴った物理学における最初の統一場理論の創出につながりました。これらの方程式の現代版はマクスウェル方程式と呼ばれています。

静電気

電荷qを持つ荷電粒子は、その電荷のみに基づく力Fを受ける。同様に、電場EもF = q Eと記述できる。これとクーロンの法則を用いると、単一の荷電粒子による電場は

${\displaystyle \mathbf {E} ={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{r^{2}}}{\hat {\mathbf {r} }}.}$

電場は保存的であるため、スカラーポテンシャルV ( r )で記述できます。

${\displaystyle \mathbf {E} (\mathbf {r} )=-\nabla V(\mathbf {r} ).}$

静磁気学

経路ℓに沿って流れる定常電流Iは、電場Bを発生させ、この電場Bは近傍の運動する荷電粒子に、上述の電場力とは量的に異なる力をかける。電流Iが近傍の速度vの電荷qに及ぼす力は、

${\displaystyle \mathbf {F} (\mathbf {r} )=q\mathbf {v} \times \mathbf {B} (\mathbf {r} ),}$

ここで、B ( r ) は磁場であり、ビオ・サバールの法則によってIから決定されます。

${\displaystyle \mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\int {\frac {Id{\boldsymbol {\ell }}\times {\hat {\mathbf {r} }}}{r^{2}}}.}$

磁場は一般に保存的ではないため、通常はスカラーポテンシャルで表すことはできません。しかし、ベクトルポテンシャルA ( r ) で表すことは可能です。

${\displaystyle \mathbf {B} (\mathbf {r} )={\boldsymbol {\nabla }}\times \mathbf {A} (\mathbf {r} )}$

電荷（黒/白）と磁極（赤/青）によるEフィールドとBフィールド。^{[ 16 ] [ 17 ]}上：電気双極子モーメントdによるEフィールド。左下： 2つの磁気単極子によって形成される数学的な磁気双極子mによるBフィールド。右下：通常の物質に見られる純粋な磁気双極子モーメントm（単極子由来ではない）によるBフィールド。

電気力学

一般に、電荷密度ρ( r , t )と電流密度J ( r , t )の両方が存在する場合、電場と磁場の両方が存在し、どちらも時間とともに変化します。これらは、 EとBをρとJに直接関連付ける微分方程式の集合であるマクスウェル方程式によって決定されます。^{[ 18 ]}

あるいは、システムをスカラーポテンシャルVとベクトルポテンシャルAで記述することもできる。遅延ポテンシャルと呼ばれる積分方程式を用いることで、ρとJからVとAを計算することができる^{[注1 ]。}そしてそこから、電場と磁場は^{[ 19 ]の関係式によって決定される。}

${\displaystyle \mathbf {E} =-{\boldsymbol {\nabla }}V-{\frac {\partial \mathbf {A} }{\partial t}}}$

${\displaystyle \mathbf {B} ={\boldsymbol {\nabla}}\times \mathbf {A} .}$

19世紀末には、電磁場は空間における2つのベクトル場の集合として理解されていました。今日では、これは時空における単一の反対称2階テンソル場として認識されています。

電荷（黒/白）と磁極（赤/青）による電界と磁極（赤/青）。^{[ 16 ] [ 17 ]}静止電荷による電界と静止磁極による磁極（自然界にはN極とS極は存在しないことに注意）。運動（速度v）においては、電荷は磁極を誘導し、磁極（自然界には存在しない）は電界を誘導する。電流は通常の電流が用いられる。

一般相対性理論における重力

一般相対論では、質量エネルギーは時空を歪ませ（アインシュタインテンソルG）、^{[ 20 ]} 、角運動量Jを持つ非対称な質量エネルギー分布を回転させることによりGEM場Hが生成される^{[ 21 ] 。}

アインシュタインの重力理論は一般相対性理論と呼ばれ、場の理論のもう一つの例です。ここでの主場は計量テンソル、つまり時空における対称的な2階テンソル場です。これはニュートンの万有引力の法則に取って代わります。

波を場として

波動は、その有限な伝播速度と、孤立した閉鎖系の単純化された物理モデルが設定された際の因果関係の性質により、物理場として構築することができる。また、波動は逆二乗則に従う。

電磁波には、光場や、回折における近傍場限界や遠方場限界といった用語が存在します。しかし実際には、光学における場の理論はマクスウェルの電磁場理論に取って代わられています。

重力波は、高さの場によって定義される水面の波です。

流体力学

流体力学には、エネルギーと運動量の保存則によって結び付けられた圧力、密度、流量の場があります。質量連続方程式は質量保存を表す 連続方程式であり 、ナビエ・ストークス方程式は流体の運動量保存を表します 。これらは、流体の 密度ρ、圧力p、偏差応力テンソルτ、および外力bがすべて与えられている場合、流体に適用されるニュートンの法則から求められます。流速uは、解くべきベクトル場です。 $${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0}$$ $${\displaystyle {\frac {\partial }{\partial t}}(\rho \mathbf {u} )+\nabla \cdot (\rho \mathbf {u} \otimes \mathbf {u} +p\mathbf {I} )=\nabla \cdot {\boldsymbol {\tau }}+\rho \mathbf {b} }$$

弾性

線形弾性はテンソル場間の 構成方程式によって定義される。

${\displaystyle \sigma _{ij}=L_{ijkl}\varepsilon _{kl}}$

ここで、 は3 × 3コーシー応力テンソルの成分、は3 × 3微小ひずみの成分、 は弾性テンソルで、81 個の成分 (通常は 21 個の独立成分) を持つ 4 階のテンソル です。${\displaystyle \sigma _{ij}}$ ${\displaystyle \varepsilon _{ij}}$ ${\displaystyle L_{ijkl}}$

熱力学と輸送方程式

温度Tが強度量、すなわち三次元空間（スカラー場）の単値微分可能関数、すなわち であると仮定すると、温度勾配は と定義されるベクトル場となる。熱伝導において、温度場はフーリエの法則に現れる。 ${\displaystyle T=T(\mathbf {r} )}$ ${\displaystyle \nablaT}$

${\displaystyle \mathbf {q} =-k\nabla T}$

ここで、q は熱流束場、k は熱伝導率です。

温度と圧力の勾配も気象学にとって重要です。

量子場

現在では量子力学はすべての物理現象の基礎となるはずであると考えられており、そのため古典場の理論は、少なくとも原理的には量子力学的な用語で書き直すことが可能であり、それに成功すれば対応する量子場の理論が得られる。例えば、古典電気力学を量子化すると量子電気力学が得られる。量子電気力学はおそらく最も成功した科学理論であり、実験データはその予測を他のどの理論よりも高い精度（より多くの有効桁数）で裏付けている。 ^{[ 22 ]} 他の2つの基本的な量子場の理論は、量子色力学と電弱理論である。

クォークのようなカラー電荷による場（Gはグルーオン場の強度テンソル）。これらは「無色」の組み合わせである。上：カラー電荷は「三元中性状態」と二元中性（電荷に類似）を持つ。下：クォーク／反クォークの組み合わせ。^{[ 16 ] [ 17 ]}

量子色力学では、色力線はグルーオンによって短距離で結合し、グルーオンは場によって分極し、場と一直線に並びます。この効果は短距離（クォークの近傍から約1 fm）で増大し、色力も短距離で増大し、クォークをハドロン内に閉じ込めます。グルーオンによって強く引き寄せられる色力線は、電荷間の電場ほど外側に「弓なり」になりません。^{[ 23 ]}

これら3つの量子場の理論は、いずれも素粒子物理学のいわゆる標準モデルの特殊なケースとして導出できます。アインシュタインの重力場の理論である一般相対性理論は、まだ量子化に成功していません。しかし、その拡張である熱場の理論は、有限温度における量子場の理論を扱っています。これは量子場の理論ではほとんど考慮されていない領域です。

BRST理論では、奇体、例えばファデーエフ・ポポフゴーストを扱います。奇古典体については、次数多様体上と超多様体上の両方で異なる記述が存在します。

古典場の場合と同様に、これまでと同様の手法を用いて、純粋に数学的な観点から量子場にアプローチすることが可能です。量子場を支配する方程式は、実際には偏微分方程式（具体的には相対論的波動方程式（RWE））です。したがって、ヤン–ミルズ場、ディラック場、クライン–ゴルドン場、シュレーディンガー場は、それぞれの方程式の解であると言えます。問題となり得るのは、これらのRWEが、特異な代数的特性を持つ複雑な数学的対象（例えば、スピノルはテンソルではないので、スピノル場には微積分が必要になる場合がある）を扱うことができることですが、適切な数学的一般化を行えば、理論上はこれらも解析的手法で扱うことができます。

場の理論

場の理論は通常、場の力学の構築、すなわち、場が時間とともに、あるいはその場が依存する他の独立した物理変数に対してどのように変化するかを規定することを指します。これは通常、場のラグランジアンまたはハミルトニアンを書き、それを無限の自由度を持つ古典力学系または量子力学系として扱うことによって行われます。結果として得られる場の理論は、古典場の理論または量子場の理論と呼ばれます。

古典場のダイナミクスは通常、場の成分に関するラグランジアン密度によって指定され、そのダイナミクスは作用原理を使用して得ることができます。

物理学の予備知識がなくても、多変数微分積分、ポテンシャル理論、偏微分方程式(PDE) などの数学だけを使用して、単純な場を構成することができます。たとえば、スカラー PDE では、波動方程式や流体力学では振幅、密度、圧力場、熱/拡散方程式では温度 / 濃度場などの量を考慮できます。物理学本来の領域 (放射測定法やコンピュータ グラフィックスなど) 以外では、光場さえあります。これらの前述の例はすべてスカラー場です。同様にベクトルについても、(応用数学的) 流体力学では変位、速度、渦度場のベクトル PDE がありますが、ベクトル場に対する微積分 (これら 3 つの量や、一般的なベクトル PDE に対する微積分と同様に) であるベクトル微積分がさらに必要になる場合があります。より一般的には、連続体力学における問題には、例えば方向性弾性（ラテン語で「伸びる」を意味する「テンソル」という用語の由来）、複雑な流体の流れ、異方性拡散などがあり、これらは行列-テンソル偏微分方程式として表され、行列またはテンソル場、つまり行列計算またはテンソル計算を必要とする。スカラー（そしてベクトル、行列、テンソル）は、どちらも抽象代数的／環論的な意味での場であるため、実数または複素数となり得る。

一般的な設定では、古典場はファイバー束の断面によって記述され、そのダイナミクスはジェット多様体（共変古典場理論）の観点から定式化される。^{[ 24 ]}

現代物理学において、最も頻繁に研究されている分野は、将来的に統一場理論につながる可能性のある 4 つの基本的な力をモデル化する分野です。

場の対称性

場（古典場または量子場）を分類する便利な方法は、その場が持つ対称性によって分類することです。物理的な対称性は通常、以下の2種類に分類されます。

時空の対称性

場は時空変換における振る舞いによって分類されることが多い。この分類に用いられる用語は以下の通りである。

• 空間の各点において単一の変数によって値が与えられるスカラー場（温度など）。この値は空間変換によって変化しません。
• ベクトル場（磁場内の各点における力の大きさと方向など）は、空間の各点にベクトルを付与することで規定されます。このベクトルの成分は、空間の回転に対して反変的に相互に変換されます。同様に、双対ベクトル場（または共ベクトル場）は、空間の各点に双対ベクトルを付与し、各双対ベクトルの成分は共変的に変換されます。
• テンソル場（結晶の応力テンソルなど）は、空間の各点におけるテンソルによって規定されます。空間内での回転により、テンソルの成分は、共変添字と反変添字の数に依存する、より一般的な方法で変換されます。
• スピノル場（ディラックスピノルなど）は量子場理論で出現し、スピンを持つ粒子が成分の 1 つを除いてベクトルのように変換することを記述します。言い換えると、ベクトル場を特定の軸の周りで 360 度回転させると、ベクトル場はそれ自身の方向を向きますが、スピノルは同じ場合に負の方向を向きます。

内部対称性

場は時空対称性に加えて内部対称性を持つことがあります。多くの場合、時空スカラーのリスト（φ ₁、φ ₂、… φ _N）である場が必要になります。例えば、天気予報では、温度、気圧、湿度などがこれに当たります。素粒子物理学では、クォークの相互作用における色対称性、すなわち強い相互作用における色対称性が内部対称性の一例です。その他の例としては、アイソスピン、弱いアイソスピン、ストレンジネス、その他のフレーバー対称性などが挙げられます。

時空を介さずに問題の対称性が存在し、その対称性の下でこれらの要素が互いに変換する場合、この対称性の集合は内部対称性と呼ばれます。また、内部対称性の下で場の電荷を分類することもできます。

統計場理論

統計場理論は、場の理論的パラダイムを多体系や統計力学へと拡張しようとするものである。上述のように、統計場理論は、通常の無限自由度論の議論によってアプローチすることができる。

統計力学が量子力学と古典力学の間にある程度の重複を持つのと同様に、統計場の理論は量子場の理論と古典場の理論の両方と関連しており、特に前者とは多くの手法を共有している。重要な例として平均場理論が挙げられる。

連続ランダムフィールド

電磁場などの上記のような古典場は、通常は無限回微分可能な関数ですが、ほとんどの場合、2回微分可能です。対照的に、一般化された関数は連続ではありません。有限温度での古典場を注意深く扱う場合、熱的に変動する古典場はどこでも微分可能ではないため、連続ランダム場の数学的手法が使用されます。ランダム場はランダム変数のインデックス付き集合です。連続ランダム場は、関数の集合をそのインデックス集合として持つランダム場です。特に、連続ランダム場のインデックス集合として関数のシュワルツ空間を取ることが数学的に都合が良い場合が多く、その場合、連続ランダム場は調整分布になります。

連続確率場は、（非常に）大まかに言えば、ほぼどこにでも存在する通常の関数として考えることができます。しかし、任意の有限領域におけるすべての無限大の加重平均をとると、有限の結果が得られます。無限大は明確に定義されていませんが、有限値は、有限値を得るための重み関数として用いられる関数と関連付けることができ、その関数は明確に定義できます。連続確率場は、関数空間から実数への線型写像として十分に定義できます。 ${\displaystyle \pm \infty}$

参照

• 共形場理論
• 共変ハミルトン場理論
• 電界強度
• ラグランジアンとオイラーの体指定
• スカラー場理論
• 速度場

注記

1. これはゲージの正しい選択に依存します。VとA はρとJによって完全に決定されるのではなく、ゲージと呼ばれるスカラー関数f ( r , t ) の範囲でのみ決定されます。遅延ポテンシャル形式論では、ローレンツゲージを選択する必要があります。

参考文献

1. ジョン・グリビン (1998). 『Qは量子：素粒子物理学AからZ』 ロンドン: ワイデンフェルド＆ニコルソン. p. 138. ISBN 0-297-81752-3。
2. リチャード・ファインマン (1970). 『ファインマン物理学講義第2巻』. アディソン・ウェスリー・ロングマン. ISBN 978-0-201-02115-8「場」とは、空間内の異なる地点で異なる値をとる物理量のことです。
3. エルナン・マクマリン (2002). 「物理学における場の概念の起源」(PDF) . Phys. Perspect . 4 (1): 13– 39. Bibcode : 2002PhP.....4...13M . doi : 10.1007/s00016-002-8357-5 . S2CID 27691986 . 
4. SE, Windyty. 「予報通りの風」 . Windy.com/ . 2021年6月25日閲覧。
5. 講義 1 | 量子もつれ、パート 1 (スタンフォード)、Leonard Susskind、スタンフォード、ビデオ、2006 年 9 月 25 日。
6. リチャード・P・ファインマン (1970). 『ファインマン物理学講義第1巻』. アディソン・ウェスリー・ロングマン.
7. リチャード・P・ファインマン (1970). 『ファインマン物理学講義第2巻』. アディソン・ウェスリー・ロングマン.
8. ジョン・アーチボルド・ウィーラー (1998). 『ジェオン、ブラックホール、そして量子泡：物理学の人生』 ロンドン: ノートン. p.  163. ISBN 9780393046427。
9. リチャード・P・ファインマン (1970). 『ファインマン物理学講義第1巻』. アディソン・ウェスリー・ロングマン.
10. スティーブン・ワインバーグ（2013年11月7日）「物理学：私たちが知っていること、知らないこと」ニューヨーク・レビュー・オブ・ブックス60 （ 17）。
11. Weinberg, Steven (1977). 「統一性の探求：量子場の理論史のためのノート」Daedalus . 106 (4): 17– 35. JSTOR 20024506 . 
12. ローランズ、ピーター (2017). 『ニュートン ― イノベーションと論争』ワールド・サイエンティフィック・パブリッシング109ページ. ISBN 9781786344045。
13. グッディング、デイヴィッド（1981年1月1日）「場の理論への最終段階：ファラデーによる磁気現象の研究、1845-1850年」物理科学史研究. 11 (2): 231–275 . doi : 10.2307/27757480 . JSTOR 27757480 . 
14. McMullin, Ernan (2002年2月). 「[タイトルが見つかりません]」 . Physics in Perspective . 4 (1): 13– 39. Bibcode : 2002PhP.....4...13M . doi : 10.1007/s00016-002-8357-5 .
15. ダニエル・クレップナー、ロバート・コレンコウ『力学入門』p.85。
16. パーカー, CB (1994).マグロウヒル物理学百科事典（第2版）. マグロウヒル. ISBN 0-07-051400-3。
17. M. Mansfield; C. O'Sullivan (2011). 『物理学を理解する』（第4版）. John Wiley & Sons. ISBN 978-0-47-0746370。
18. グリフィス、デイビッド.電気力学入門（第3版）. p. 326.
19. ワングスネス、ロアルド.電磁場（第2版）.p.469.
20. JA Wheeler; C. Misner; KS Thorne (1973). 『重力』 WH Freeman & Co. ISBN 0-7167-0344-0。
21. I. Ciufolini; JA Wheeler (1995). 『重力と慣性』プリンストン物理学シリーズ. ISBN 0-691-03323-4。
22. ,マイケル・E.; シュローダー, ダニエル・V. (1995). 『量子場入門』ウェストビュー・プレス. p.  198. ISBN 0-201-50397-2。QED の精度テストも参照してください。
23. R. Resnick; R. Eisberg (1985). 『原子、分子、固体、核、粒子の量子物理学』（第2版）John Wiley & Sons. p.  684. ISBN 978-0-471-87373-0。
24. Giachetta, G., Mangiarotti, L., Sardanashvily, G. (2009) Advanced Classical Field Theory . シンガポール: World Scientific, ISBN 978-981-283-895-7（arXiv：0811.0331）

さらに読む

• 「フィールド」.物理科学原理. 第25巻（第15版）. 1994年. 815ページ – Encyclopædia Britannica (Macropaedia)より。
• ランダウ、レフ・D.、リフシッツ、エフゲニー・M. (1971). 『古典体論』（第3版）. ロンドン: ペルガモン. ISBN 0-08-016019-0理論物理学講座第2巻。
• ジェプセン、キャサリン（2013年7月18日）「リアルトーク：すべては場からできている」（PDF）Symmetry Magazine。2016年3月4日時点のオリジナル（PDF）からアーカイブ。 2015年6月9日閲覧。

外部リンク

• 粒子場と高分子場の理論