電磁気学入門
電磁気学のトピックに関する非技術的な入門

電磁気力は自然界の基本的な力の一つです。かつては、電気と磁気は別々に研究され、別々の現象とみなされていました。 ハンス・クリスチャン・エルステッドは、この二つは関連しており、電流が磁気を生じることを発見しました。 マイケル・ファラデーは逆に、磁気が電流を誘導できることを発見し、ジェームズ・クラーク・マクスウェルはこれらすべてを電磁気学の統一理論にまとめました。 マクスウェルの方程式はさらに電磁波の存在を示し、ハインリヒ・ヘルツの実験はこれを確認し、無線を可能にしました。マクスウェルはまた、光も電磁波の一種であると正しく仮定し、これにより光学はすべて電磁気学の一分野となりました。 無線波と光の違いは、前者の 波長が後者よりもはるかに長いことだけです。アルバート・アインシュタインは、磁場は電場の相対論的運動によって生じるため、磁気は電気の副作用に過ぎないことを示しました。現代の理論的には、電磁気学は量子電気力学において量子場として扱われます。

電気工学に関連する多くの状況では、正しい結果を得るために量子論を適用する必要がありません。 古典物理学は、巨視的な物体が関わるほとんどの状況において、依然として正確な近似値となります。いくつかの例外を除けば、量子論は原子スケールでのみ必要であり、より単純な古典的処理を適用できます。限られた状況では、処理をさらに簡略化することも可能です。 静電気学は定常電荷のみを扱うため、磁場は発生せず、考慮されません。 永久磁石は、電気や電磁気学を参照せずに記述できます。 回路理論は、電流が流れる導体の周囲に磁場がほぼ閉じ込められている電気回路網を扱います。このような回路では、マクスウェル方程式さえも不要となり、より単純な定式化を使用できます。一方、電磁気学の量子的処理は化学において重要です。 化学反応と化学結合は、原子の周りの電子の量子力学的相互作用の結果です。トンネルダイオードなど、多くの電子デバイスの挙動を説明するには、量子論的考慮も必要です。

電荷

クーロンの法則によれば、同種の電荷は反発し、異種の電荷は引き合うとされます。

電磁気力は、重力、強い力、弱い力と並んで、自然界の基本的な力の一つです。重力は質量を持つすべてのものに作用しますが、電磁気力は電荷を持つすべてのものに作用します。さらに、質量が生成も消滅もしないという質量保存の法則があるように、電荷保存の法則もあり、閉鎖系（電荷が出入りしない系）の電荷は一定のままでなければなりません。[1]古典物理学において、質量のある物体にかかる重力の力を説明する基本法則は、ニュートンの万有引力の法則です。同様に、クーロンの法則は、荷電物体が互いに及ぼす力を説明する基本法則です。これは次の式で与えられます。

F ＝ け e q 1 q 2 r 2 {\displaystyle F=k_{\text{e}}{q_{1}q_{2} \over r^{2}}}

ここで、 Fは力、k eはクーロン定数、q 1とq 2は2つの電荷の大きさ、 r 2はそれらの間の距離の2乗です。これは、同種の電荷は互いに反発し、異種の電荷は互いに引き合うという事実、そして粒子の電荷が強いほど、それらが互いに及ぼす力が強くなるという事実を説明しています。この法則は逆2乗の法則でもあり、 2つの粒子間の距離が2倍になると、それらに及ぼす力は4分の1に減少することを意味します。[2]

電場と磁場

電界線は正電荷から負電荷へと向かいます。
電場 (左) と磁場 (右) によって正電荷に及ぼされる力が組み合わさって、ローレンツ力が生じます。

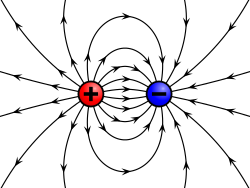
物理学において、場とは物質と相互作用する実体であり、空間と時間の各点に値を割り当てることで数学的に記述できます。ベクトル場とは、空間と時間の各点において数値と方向の両方が割り当てられた場です。電荷は電場と呼ばれるベクトル場を生成します。電場の数値（電場強度とも呼ばれます）は、荷電粒子が電場内で感じる電気力の強さを決定し、電場の方向は力がどの方向に働くかを決定します。

慣例的に、電場の方向は正電荷に働く力の方向と同じであり、負電荷に働く力の方向とは反対である。[3] [4] 正電荷は他の正電荷から反発され、負電荷に引き寄せられるため、電場は正電荷から離れて負電荷に向かう。電場のこれらの性質は、電場を用いて表される電荷​​に働く電気力の式に要約される。 ここで、Fは電場Eにおける電荷qに働く力である。[4] [5] F ＝ q E {\displaystyle F=qE}

荷電粒子は電場を生成するだけでなく、運動状態にあるときには磁場も生成し、その磁場は他の運動している電荷（および永久磁石）によって感知されます。[6]磁場から運動している電荷に働く力の方向は、運動方向と磁力線の方向の両方に垂直であり、右手の法則を使用して求めることができます。力の強さは次式で与えられます。 ここで、Fは磁場B中の速度vの電荷qに働く力であり、磁場Bは電荷の運動方向から角度θの方向を向いています。 [7] F ＝ q v B 罪 ⁡ θ {\displaystyle F=qvB\sin \theta }

荷電粒子に働く電気力と磁気力の組み合わせは、ローレンツ力と呼ばれます。[7] [8] 古典的電磁気学は、マクスウェル方程式と呼ばれる一連の方程式と並んで、ローレンツ力によって完全に説明されます。これらの方程式の最初のものはガウスの法則として知られています。これは、荷電粒子と電荷分布によって生成される電場を説明します。ガウスの法則によると、任意の閉じた表面を通過する電場の束（または流れ）は、その表面に囲まれた電荷の量に比例します。[9] [10]これは、電荷が大きいほど、生成される電場が大きくなることを意味します。また、他の重要な意味合いもあります。たとえば、この法則は、表面に囲まれた電荷がない場合、電場がまったく存在しないか、または閉じた表面の近くでその外側に電荷がある場合、表面への電場の流れが表面からの電場の流れと正確に打ち消される必要があることを意味します。[11]マクスウェルの2番目の方程式は磁気のガウスの法則として知られており、最初のガウスの法則と同様に磁束を記述しますが、電束ではなく磁束を記述します。磁気のガウスの法則によると、閉じた表面を通る磁場の流れは常にゼロです。これは、磁場がある場合、閉じた表面への流れが閉じた表面からの流出と常に打ち消されることを意味します。この法則は、「磁気単極子なし」とも呼ばれています。これは、閉じた表面から流出する磁束はすべてその表面に戻らなければならないことを意味するため、正と負の磁極は磁気双極子として一緒になり、磁気単極子に分離することは決してできないことを意味します。[12]これは、正と負の電荷として別々に存在できる電荷とは対照的です。

直線状の電線（左）とコイル状の電線（右）の右手の法則。鉄心に巻かれた電線に電流を流すと、電磁石が発生します。

マクスウェルの３番目の方程式は、アンペール・マクスウェルの法則と呼ばれる。これは、電流によって磁場を発生できることを述べている。[13]磁場の方向は、アンペールの右手の法則によって決まる。電線がまっすぐであれば、磁場は右手の法則で握った指のように、電線の周りに巻き付く。電線がコイル状に巻かれている場合は、コイル内の磁場は、右手の法則で伸ばした親指のように直線を指す。[14]このように電流を使って磁石を作るものを、電磁石という。電磁石では、鉄心の周りをソレノイド状に巻いた電線がよく使用され、鉄心が磁化されるため、磁場が強くなる。[15] [16]マクスウェルによるこの法則の拡張では、時間とともに変化する電場も磁場を発生できるとしている。[12]同様に、ファラデーの電磁誘導の法則は、磁場が電流を発生させることを述べています。例えば、電線コイルに磁石を押し込んだり引き抜いたりすると、コイルに電流が発生します。この電流は、磁石の強さ、コイルの数、そして磁石をコイルに出し入れする速度に比例します。この原理は、高電圧から低電圧へ、あるいはその逆へ電流を変換するために使用される変圧器にとって不可欠です。変圧器は、高圧の主電源を家庭で安全に使用できる低電圧の電気に変換するために必要です。マクスウェルによるこの法則の定式化は、時間とともに変化する磁場が電場を生成するという、マクスウェル・ファラデー方程式（マクスウェル方程式の4番目で最後の方程式）で与えられています。

電磁スペクトル

マクスウェル方程式は、電場と磁場の単一の統一理論を提供し、この理論を作成したマクスウェルの仕事は、ニュートンの万有引力の法則の最初の統一に続いて「物理学における第二の偉大な統一」と呼ばれています。[17]自由空間（電荷や電流が存在しない空間）でのマクスウェル方程式の解は、光速で伝わる電磁波（電気成分と磁気成分の両方を持つ）に対応する波動方程式を生成します。[18]これらの波動解の波動速度が光速と正確に等しいという観察から、マクスウェルは、光は電磁放射の一種であると仮説を立て、異なる波長の他の電磁放射が存在する可能性があると断言しました。[19]電磁放射の存在は、1886年から1889年にかけてのハインリヒ・ヘルツによる一連の実験で証明され、その実験で彼は電波の存在を発見しました。電磁スペクトル全体は（周波数が上昇する順に）、電波、マイクロ波、赤外線、可視光線、紫外線、X線、ガンマ線で構成されています。[20]

電磁気学のさらなる統一は、アインシュタインの特殊相対性理論によってもたらされました。特殊相対性理論によれば、互いに対して異なる速度で運動している観測者は、異なる観測参照系を占めます。ある観測者が別の観測者に対して運動している場合、彼らは長さの収縮を経験します。つまり、運動していない物体は、静止している観測者よりも運動している観測者に対してより近くに見えます。したがって、電子が中性電線の電流と同じ速度で運動している場合、電子は電線中を流れる電子は電線に対して静止しているように、そして正電荷は互いに収縮しているように体験します。実験室系では、電子は動いているため電線中の電流から磁力を感じますが、電線は中性であるため電気力は感じません。しかし、電子の静止系では、正電荷は流れる電子に比べてより近くに見えるため、電線は正に帯電しているように見えます。したがって、電子の静止系では、電子は磁力を感じません（自身の系では運動していないため）。しかし、正に帯電した電線による電気力は感じます。この相対性理論の結果は、磁場は異なる参照系における電場に過ぎず（そしてその逆もまた同様）、したがって両者は同じ根底にある電磁場の異なる現れであることを証明しています。[21] [22] [23]

導体、絶縁体、回路

指揮者

完全導体内の電荷は再配置され、内部の電界は常にゼロになります。

導体とは、電子が容易に流れる物質です。最も効果的な導体は通常、金属です。なぜなら、電子が原子核から非局在化し、陽イオンが自由電子の雲に囲まれるという自由電子モデルでかなり正確に説明できるからです。 [24]良導体の例としては、銅、アルミニウム、銀などが挙げられます。電子機器の配線は、多くの場合銅で作られています。[25]

導体の主な特性は以下の通りである。[26]

  1. 完全導体内部では電界はゼロです。導体内を電荷が自由に移動できるため、外部電界によって電荷が乱されると、電荷は導体内部で外部電界を正確に打ち消すように再配置されます。
  2. 導体内部の電位はどこでも同じであり、導体表面全体でも一定です。これは最初の記述から導き出されます。導体内部のどこでも電場はゼロであり、したがって導体内部の電位も一定だからです。
  3. 電場は導体の表面に対して垂直です。もしそうでない場合、導体表面における電場の成分はゼロではないため、導体内の電荷は電場のその成分がゼロになるまで動き回ります。
  4. 表面を通過する正味の電気束は、その表面に囲まれた電荷に比例します。これはガウスの法則を言い換えたものです。

一部の物質では、電子は原子核に束縛されているため自由に動き回ることができませんが、電子を解放するために必要なエネルギーは低いです。半導体と呼ばれるこれらの物質では、低温では導電性が低くなりますが、温度が上昇すると電子がより多くの熱エネルギーを獲得し、導電性が高まります。[27]シリコンは、太陽からの光子から受け取るエネルギーが増えるほど導電性が高くなる太陽電池の製造に使用できる半導体の一例です。 [28]

超伝導体は、ある臨界温度以下に冷却されると、電子の流れに対する抵抗がほとんど、あるいは全くなくなる物質です。超伝導は、2つのフェルミオン（電子もフェルミオンの一種）が全く同じ量子状態をとることはできないという量子力学のパウリの排他原理によってのみ説明できます。超伝導体では、ある温度以下では電子がボソン結合対を形成しますが、これはこの原理に従わず、すべての電子が同じエネルギー準位に低下し、電流中を均一に移動することを意味します。[29]

絶縁体

誘電体材料では、電界によって材料が分極することがあります。

絶縁体は電子の流れに対して高い抵抗性を持つ物質であるため、安全のために導線を覆うためによく使用されます。絶縁体では、電子は原子核にしっかりと結合しており、それらを解放するためのエネルギーが非常に高いため、自由に移動できず、外部電場による誘導運動に対して抵抗性を持ちます。 [30]しかし、誘電体と呼ばれる一部の絶縁体は、外部電場の影響下で分極することができ、電荷がわずかに変位して双極子を形成し、正と負の側を作り出します。[31]誘電体はコンデンサに使用され、コンデンサプレート間の電場により多くの電位エネルギーを蓄えることができます。[32]

コンデンサ

平行板コンデンサ

コンデンサは、2枚の反対の電荷を持つ導電板の間に電界をかけて電位エネルギーを蓄える電子部品です。一方の導電板の電荷密度が+ Q/A 、もう一方の導電板の電荷密度が-Q/A （Aは導電板の面積）の場合、両者の間に電界が生じます。2枚の平行板間の電位差Vは、数学的に次のように表すことができます[33]。

V ＝ 質問 d ε 0 あ {\displaystyle V={Qd \over \varepsilon _{0}A}}

ここで、dはプレート間隔、は自由空間の誘電率である。コンデンサが電気ポテンシャルエネルギーを蓄える能力は、次のように定義される静電容量によって測定される。平行板コンデンサの場合、これは[33]である。 ε 0 {\textstyle \varepsilon _{0}} C ＝ 質問 / V {\textstyle C=Q/V}

C ＝ ε 0 あ d {\displaystyle C={\varepsilon _{0}A \over d}}

プレート間に誘電体を配置すると、自由空間の誘電率に誘電体の比誘電率が乗じられ、静電容量が増加します。[32]コンデンサに蓄えられる最大エネルギーは、静電容量とプレート間の電位差の2乗に比例します。[33]

E ＝ 1 2 C V 2 {\displaystyle E={\frac {1}{2}}CV^{2}}

インダクタ

インダクタは、コイル内の磁場にエネルギーを蓄える電子部品です。電流を流すコイルは、アンペールの回路法則に従って磁場を誘導します。電流Iが大きいほど、磁場に蓄えられるエネルギーは大きくなり、コイルによって生成される磁束で定義されるインダクタンスは低くなります。インダクタンスは電流の変化に対する回路の抵抗の尺度であり、高いインダクタンスを持つインダクタは交流電流に抵抗するためにも使用できます。[34] L ＝ Φ B / 私 {\textstyle L=\Phi _{B}/I} Φ B {\textstyle \Phi _{B}}

その他の回路部品

成分 主な機能 回路図記号
抵抗器 電流の流れを妨げる
バッテリー 電源として機能する
直流電圧源 一方向に向かう一定の電流である直流（DC）の供給源として機能する
AC電圧源 定期的に方向が反転する変動電流である交流電流（AC）の供給源として機能する
ダイオード 電流は一方向には容易に流れるが、他の方向には流れない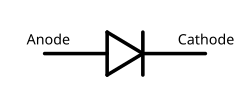
コンデンサ 電界にエネルギーを蓄え、電荷を蓄え、低周波の交流電流を流す
インダクタ 磁場にエネルギーを蓄え、電流の変化に抵抗する

巡回法

回路理論は、電流を流す導体の周囲に電界がほぼ閉じ込められている電気回路網を扱います。このような回路では、回路の挙動すべてを電磁気学の法則から直接導く代わりに、単純な回路法則を用いることができます。オームの法則は、抵抗Rと呼ばれる量を導入することで、回路の電流Iと電圧Vの関係を規定します[35]。

オームの法則: 私 ＝ V / R {\displaystyle I=V/R}

電力は次のように定義されるので、オームの法則は回路の電力を他の量で表すのに使用できる[36] P ＝ 私 V {\displaystyle P=IV}

P ＝ 私 V ＝ V 2 / R ＝ 私 2 R {\displaystyle P=IV=V^{2}/R=I^{2}R}

キルヒホッフの接合則は、接合（またはノード）に流入する電流と流出する電流が等しくなければならないというものです。これは電荷保存則から導かれます。電流は時間経過に伴う電荷の流れとして定義されるからです。電流が接合から流出する際に分岐する場合、分岐した電流の合計は流入する回路に等しくなります。[37]

キルヒホッフのループ則は、回路の周りの閉ループ内の電圧の合計がゼロになるというものです。これは電場が保存則であるという事実に由来し、つまり、どのような経路をたどっても、ある点の電位はそこに戻っても変化しないことを意味します。[37]

規則は直列回路と並列回路における電流や電圧などの量をどのように合計するかを教えてくれます。[37]

直列回路の場合、各コンポーネントの電流は同じままで、電圧と抵抗が加算されます。

V t o t ＝ V 1 + V 2 + V 3 + … R t o t ＝ R 1 + R 2 + R 3 + … 私 ＝ 私 1 ＝ 私 2 ＝ 私 3 ＝ … {\displaystyle V_{tot}=V_{1}+V_{2}+V_{3}+\ldots \qquad R_{tot}=R_{1}+R_{2}+R_{3}+\ldots \qquad I=I_{1}=I_{2}=I_{3}=\ldots }

並列回路の場合、各コンポーネントの電圧は同じままで、電流と抵抗は次のように関係します。

V t o t ＝ V 1 ＝ V 2 ＝ V 3 ＝ … 1 R t o t ＝ 1 R 1 + 1 R 2 + 1 R 3 + … 私 t o t ＝ 私 1 + 私 2 + 私 3 + … {\displaystyle V_{tot}=V_{1}=V_{2}=V_{3}=\ldots \qquad {1 \over R_{tot}}={1 \over R_{1}}+{1 \over R_{2}}+{1 \over R_{3}}+\ldots \qquad I_{tot}=I_{1}+I_{2}+I_{3}+\ldots }

参照

参考文献

  1. ^ パーセル、エドワード・M.（2013年1月21日）『電気と磁気』（第3版）ケンブリッジ社、  pp.3-4、ISBN 978-1-107-01402-2. OCLC  805015622。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  2. ^ ウォーカー、ジェール（1945-）（2011年）『物理学の基礎』、ハリデー、デイビッド（1916-2010）、レスニック、ロバート（1923-2014）共著（第9版）、ホーボーケン、ニュージャージー州：ワイリー、578頁。ISBN 978-0-470-46911-8. OCLC  435710913。{{cite book}}: CS1 maint: 複数名: 著者リスト (リンク) CS1 maint: 数値名: 著者リスト (リンク)
  3. ^ Pumplin, Jon (2000). 「電界線」ミシガン州立大学物理学部. 2018年10月18日閲覧。
  4. ^ ab Nave, R. 「電界」.ジョージア州立大学ハイパー物理学. 2018年10月16日閲覧。
  5. ^ パーセル、エドワード・M.（2013年1月21日）『電気と磁気』（第3版）ケンブリッジ社、p.7、ISBN 978-1-107-01402-2. OCLC  805015622。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  6. ^ 「ファインマン物理学講義 第2巻 第1章 電磁気学」feynmanlectures.caltech.edu . 2018年10月30日閲覧。
  7. ^ ab 「磁力」. hyperphysics.phy-astr.gsu.edu . 2020年11月26日閲覧。
  8. ^ パーセル、エドワード・M.（2013年1月21日）『電気と磁気』（第3版）ケンブリッジ社、277頁。ISBN 978-1-107-01402-2. OCLC  805015622。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  9. ^ Grant, I.S. (Ian S.) (1990).電磁気学. マンチェスター物理学シリーズ. Phillips, WR (William Robert) (第2版). チチェスター [イギリス]: Wiley. pp.  17– 22. ISBN 0-471-92711-2. OCLC  21447877。
  10. ^ 「ガウスの法則」. hyperphysics.phy-astr.gsu.edu . 2018年10月30日閲覧。
  11. ^ 「ファインマン物理学講義 第2巻 第4章 静電気、S5：Eの磁束」feynmanlectures.caltech.edu . 2020年11月27日閲覧。
  12. ^ ab パーセル, エドワード M. (2013年1月21日).電気と磁気（第3版）. ケンブリッジ. p. 322. ISBN 978-1-107-01402-2. OCLC  805015622。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  13. ^ 「アンペールの法則」. hyperphysics.phy-astr.gsu.edu . 2020年11月27日閲覧。
  14. ^ Grant, I.S. (Ian S.) (1990).電磁気学. マンチェスター物理学シリーズ. Phillips, WR (William Robert) (第2版). チチェスター [イギリス]: Wiley. p. 125. ISBN 0-471-92711-2. OCLC  21447877。
  15. ^ 「磁石と電磁石」hyperphysics.phy-astr.gsu.edu . 2020年11月27日閲覧。
  16. ^ “強磁性”. hyperphysics.phy-astr.gsu.edu . 2020年11月27日閲覧。
  17. ^ 編集者、AccessScience (2014). 「統一理論と万物の理論」 . Access Science . doi :10.1036/1097-8542.BR0814141. {{cite journal}}:|last=一般的な名前があります（ヘルプ）
  18. ^ グラント、イアン・S. (1990).電磁気学. マンチェスター物理学シリーズ. フィリップス、WR（ウィリアム・ロバート）（第2版）. チチェスター [イギリス]: ワイリー. p. 365. ISBN 0-471-92711-2. OCLC  21447877。
  19. ^ マクスウェル、ジェームズ・クラーク (1865). 「電磁場の動的理論」(PDF) .ロンドン王立協会哲学論文集. 155 : 459–512 .書誌コード:1865RSPT..155..459M. doi :10.1098/rstl.1865.0008. S2CID 186207827. 2011年7月28日時点のオリジナルより アーカイブ(PDF).光と磁気は同じ物質の作用である (p.499)
  20. ^ 「電磁スペクトルと分光法入門 | 分析化学 | PharmaXChange.info」pharmaxchange.info . 2011年8月25日. 2020年11月26日閲覧。
  21. ^ パーセル、エドワード・M. (2013).電気と磁気（第3版）. ケンブリッジ. pp.  235–68 . ISBN 978-1107014022. OCLC  805015622。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  22. ^ 「ファインマン物理学講義 第2巻 第13章 静磁気学」feynmanlectures.caltech.edu . 2018年10月30日閲覧。
  23. ^ A. French (1968)特殊相対性理論、第8章「相対性理論と電気」、pp. 229–65、WW Norton。
  24. ^ Hook, JR, Hall, HE (2010). Solid State Physics (第2版). Chichester, West Sussex, UK: John Wiley & Sons. pp.  76– 77. ISBN 978-1-118-72347-0. OCLC  868939953。{{cite book}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  25. ^ 「電気伝導性に優れた金属とは？」サイエンシズ誌、2018年4月10日。 2020年11月27日閲覧。
  26. ^ パーセル、エドワード・M. (2013).電気と磁気（第3版）. ケンブリッジ. p. 129. ISBN 978-1107014022. OCLC  805015622。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  27. ^ 「ファインマン物理学講義 第3巻 第14章 半導体」feynmanlectures.caltech.edu . 2020年11月26日閲覧。
  28. ^ 「太陽電池の仕組み」アメリカ化学会. 2020年11月26日閲覧。
  29. ^ 「ファインマン物理学講義 第3巻 第21章 古典的な文脈におけるシュレーディンガー方程式：超伝導セミナー」feynmanlectures.caltech.edu . 2020年11月26日閲覧。
  30. ^ 「導体と絶縁体」hyperphysics.phy-astr.gsu.edu . 2020年11月27日閲覧。
  31. ^ 「誘電体 | 物理学」ブリタニカ百科事典. 2020年11月27日閲覧。
  32. ^ ab 「誘電体」. hyperphysics.phy-astr.gsu.edu . 2020年11月27日閲覧。
  33. ^ abc Grant, I.S. (Ian S.) (1990).電磁気学. マンチェスター物理学シリーズ. Phillips, WR (William Robert) (第2版). チチェスター [イギリス]: Wiley. pp.  41– 42. ISBN 0-471-92711-2. OCLC  21447877。
  34. ^ パーセル、エドワード・M.（2013年1月21日）『電気と磁気』（第3版）ケンブリッジ社、374ページ。ISBN 978-1-107-01402-2. OCLC  805015622。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  35. ^ 「オームの法則」. hyperphysics.phy-astr.gsu.edu . 2020年11月27日閲覧。
  36. ^ “電力”. hyperphysics.phy-astr.gsu.edu . 2020年11月27日閲覧。
  37. ^ abc Young, HD, Freedman, RA (2016). Sears and Zemansky's University Physics with Modern Physics (第14版). ボストン: Pearson . pp.  872– 878. ISBN 978-0-321-97361-0. OCLC  897436903。{{cite book}}: CS1 maint: 複数の名前: 著者リスト (リンク)
Retrieved from "https://en.wikipedia.org/w/index.php?title=Introduction_to_electromagnetism&oldid=1322661025"