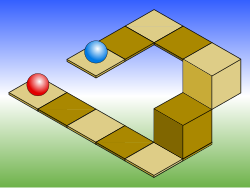
等角投影

| シリーズの一部 |
| グラフィカル投影 |
|---|
 |
等角投影法は、技術図面や工学図面において、三次元の物体を二次元で視覚的に表現する方法です。三本の座標軸が均等に短縮され、どの二軸間の角度も120度となる 軸測投影法です。
概要

「等尺性」という用語はギリシャ語で「等しい尺度」を意味し、投影の各軸に沿ったスケールが同じであることを反映しています (他の形式のグラフィカル投影とは異なります)。
オブジェクトの等角投影ビューは、x、y、z軸の投影間の角度がすべて同じ、つまり 120° になるように視線方向を選択することで取得できます。たとえば、立方体の場合、最初に 1 つの面をまっすぐ見ることでこれを実現します。次に、立方体を垂直軸を中心に ±45° 回転させ、続いて水平軸を中心に約 35.264° (正確には arcsin 1 ⁄ √ 3または arctan 1 ⁄ √ 2で、マジック角に関連) 回転させます。立方体 (画像を参照) の場合、結果として得られる 2D 図面の周囲は完全な正六角形になることに注意してください。つまり、すべての黒い線の長さが等しく、立方体の面はすべて同じ面積です。等角グラフ用紙を通常の画用紙の下に置くと、計算なしでこの効果を得ることができます。
同様の方法で、 3Dシーンでアイソメトリックビューを取得できます。カメラを床と平行に配置し、座標軸に合わせ、まず水平方向(垂直軸を中心に)に±45°回転させ、次に水平軸を中心に35.264°回転させます。
等角投影を視覚化する別の方法は、立方体の部屋を上の角から始めて、反対側の下の角に向かって眺める様子を考えることです。X軸は右下斜め方向に伸び、Y軸は左下斜め方向に伸び、Z軸は真上を向いています。奥行きは画像の高さによっても表されます。各軸に沿って引かれた線は、互いに120°の角度をなしています。
これらすべてのケースでは、すべての軸測投影および正投影の場合と同様に、投影された長さがカメラからの距離によって変化しないようにするために、このようなカメラには物体空間テレセントリック レンズが必要になります。
「等角投影」という用語は、しばしば軸測投影を指すものとして誤って使用されます。しかし、実際には軸測投影には、等角投影、二角投影、斜投影の3種類があります。
回転角度
等角投影に必要な 2 つの角度から、2 番目の角度の値は直感に反するように思われるかもしれません。そのため、もう少し説明が必要です。まず、長さが 2 の辺を持ち、中心が軸の原点にある立方体を想像してみましょう。つまり、すべての面が原点から 1 の距離で軸と交差します。ピタゴラスの定理を使用すると、中心から任意の辺の中央までの線の長さは√ 2と計算できます。立方体をx軸上で 45° 回転させると、図に示すように、点 (1, 1, 1) は (1, 0, √ 2 ) になります。2 番目の回転は、同じ点を正のz軸上に持ってくることを目的としているため、 1 ⁄ √ 2の逆正接、つまり約 35.264°に等しい値の回転を実行する必要があります。
数学
等角投影図を得るには、観察者がどの八分円を向いているかに応じて、8つの異なる方向があります。3次元空間の点a x , y , zから、最初の八分円を向いている2次元空間の点b x , yへの等角投影変換は、回転行列を用いて数学的に次のように表すことができます。
ここで、α = arcsin(tan 30°) ≈ 35.264°、β = 45°です。上で説明したように、これは垂直軸(ここではy )を中心にβ だけ回転させ、続いて水平軸(ここではx)を中心にαだけ回転させます。そして、これをxy平面に正投影します。
他の7つの可能性は、反対側に回転するかしないか、そして視線方向を反転するかしないかによって得られます。[ 1 ]
歴史と限界
等長投影法の概念は、ウィリアム・ファリッシュ教授(1759-1837)によって初めて形式化されましたが、何世紀にもわたって大まかな経験的な形で存在していました。[ 3 ] [ 4 ] 19世紀半ばから、等長投影法は「エンジニアにとって非常に貴重なツールとなり、その後まもなく、軸測図法と等長投影図法はヨーロッパとアメリカの建築研修コースのカリキュラムに組み込まれました」[ 5 ] 。しかし、ヤン・クリッケ(2000) [ 6 ]によると、「軸測図法は中国で生まれました。中国美術におけるその役割は、ヨーロッパ美術の線遠近法に似ていました。軸測図法とそれに伴う絵画的文法は、ビジュアルコンピューティングの出現により新たな重要性を帯びてきました」[ 6 ] 。
あらゆる平行投影法と同様に、等角投影法で描かれた物体は、観察者に近づいたり遠ざかったりしても、大きく見えたり小さく見えたりしません。直接測定が必要な建築図面には有利ですが、透視投影法とは異なり、人間の視覚や写真の通常の動作とは異なるため、結果として歪みが生じます。また、右図や上図に示すように、奥行きや高度の測定が困難な状況になりやすいです。これにより、ペンローズ階段のように、矛盾した、あるいは不可能な形状が作られることがあります。
ビデオゲームやピクセルアートでの使用
アイソメトリックなビデオゲームグラフィックスは、ビデオゲームやピクセルアートで用いられる平行投影を利用したグラフィックスであるが、視点に角度をつけることで、上から見た視点や側面からの視点では見えない環境の側面を明らかにし、 3次元効果を生み出す。名前にもかかわらず、アイソメトリックなコンピュータグラフィックスは必ずしも真のアイソメトリックではない。つまり、x、y、z軸は、必ずしも互いに 120° の方向を向いているわけではない。代わりに、さまざまな角度が使用され、最も一般的なのは二次元投影と 2:1 のピクセル比である。「 3 ⁄ 4パースペクティブ」、「3 ⁄ 4ビュー」、「2.5D 」、「疑似 3D」という用語も使用されることがあるが、これらの用語は他の文脈では多少異なる意味を持つことがある。
かつては一般的だったアイソメトリック投影は、より強力な3Dグラフィックシステムの登場と、ビデオゲームがアクションや個々のキャラクターに重点を置くようになったことで、あまり使用されなくなりました。[ 7 ]しかし、アイソメトリック投影を利用したビデオゲーム、特にコンピュータロールプレイングゲームは、近年、インディーゲームシーンで復活を遂げています。[ 7 ] [ 8 ]
参照
参考文献
- ^ Ingrid Carlbom; Joseph Paciorek; Dan Lim (1978年12月). 「平面幾何投影とビューイング変換」. ACM Computing Surveys . 10 (4): 465– 502. CiteSeerX 10.1.1.532.4774 . doi : 10.1145/356744.356750 . S2CID 708008 .
- ^ウィリアム・ファリッシュ (1822)「等尺性遠近法について」ケンブリッジ哲学論文集1 (1822)。
- ^バークレー・G・ジョーンズ (1986).自然災害からの歴史的建造物と博物館コレクションの保護. ミシガン大学. ISBN 0-409-90035-4. p.243.
- ^チャールズ・エドマンド・ムーアハウス (1974).ビジュアルメッセージ:高学年向けのグラフィックコミュニケーション.
- ^ J. Krikke (1996). 「サイバースペースに対する中国の視点? 2016年2月5日アーカイブ、 Wayback Machine」。国際アジア研究所ニュースレター、9、1996年夏。
- ^ a b Jan Krikke (2000). 「軸測図法:視点の問題」.コンピュータグラフィックスとアプリケーション, IEEE 2000年7月/8月. 第20巻 (4), pp. 7–11.
- ^ a b Signor, Jeremy (2014年12月19日). 「Retronauts: The Continued Relevance of Isometric Games」 . usgamer.net . Gamer Network. 2022年9月25日時点のオリジナルよりアーカイブ。 2017年4月1日閲覧。
- ^ Vas, Gergo (2013年3月18日). 「最も見栄えの良いアイソメトリックゲーム」 . kotaku.com . Gizmodo Media Group. 2021年10月10日時点のオリジナルよりアーカイブ。2017年4月1日閲覧。