等周点

三角形の中心

幾何学において、等周点（いしょうせんてん、英: isoperimetric point）とは、三角形の中心、つまり平面三角形に関連付けられた特別な点である。この用語は、1985年にアメリカ数学月刊誌に掲載された論文においてGR Veldkampによって初めて導入された。三角形 $△$ $ABC$ の平面上の点 $Pは、三角形$ $△$ $PBC$ $、 △$ $PCA$ $、 △$ $PAB の$ 周長が等しいという性質を持つ。つまり、^[1]^[2]

${\begin{aligned}&{\overline {PB}}+{\overline {BC}}+{\overline {CP}},\\=\ &{\overline {PC}}+{\overline {CA}}+{\overline {AP}},\\=\ &{\overline {PA}}+{\overline {AB}}+{\overline {BP}}.\end{aligned}}$

フェルトカンプの意味での等周点は、特定の条件を満たす三角形にのみ存在する。 $△ ABC$ のフェルトカンプの意味での等周点が存在する場合、その三線座標は次のようになる。^[3]

$\sec {\tfrac {A}{2}}\cos {\tfrac {B}{2}}\cos {\tfrac {C}{2}}-1\ :\ \sec {\tfrac {B}{2}}\cos {\tfrac {C}{2}}\cos {\tfrac {A}{2}}-1\ :\ \sec {\tfrac {C}{2}}\cos {\tfrac {A}{2}}\cos {\tfrac {B}{2}}-1$

任意の三角形 $△ ABC$ に対して、上記のような三線座標を持つ点 $P$ を関連付けることができます。この点は三角形の中心であり、クラーク・キンバリングの『三角形の中心事典』（ETC）では三角形 $△ ABC$ の等周点と呼ばれています。これは三角形の中心X (175) で表されます。^[4]点X (175)は、フェルトカンプの意味で三角形 $△ ABC$ の等周点である必要はありません。しかし、フェルトカンプの意味で三角形 $△ ABC$ の等周点が存在する場合、それは点X (175) と同一になります。

$三角形△$ $PBC$ $、△$ $PCA$ $、△$ $PABの$ 周囲長が等しいという性質を持つ点 $Pは、1890年に$ エミール・ルモワーヌの論文ですでに研究されている。^[4]^[5]

フェルドカンプの意味での等周点の存在

$△ ABC を$ 任意の三角形とする。この三角形の辺の長さを $a, b, c$ とする。その外接半径を $R$ 、内接半径を $r$ とする。フェルトカンプの意味で等周点が存在するための必要十分条件は、以下のように述べられる。^[1]

三角形

△ ABCが

フェルトカンプの意味で等周点を持つのは、

a+b+c>4R+r.

すべての鋭角三角形 $△ ABCについて、$ $a + b + c > 4 R + r$ が成り立ち、したがってすべての鋭角三角形は、フェルドカンプの意味で等周点を持ちます。

プロパティ

$三角形△$ $ABC$ の三角形の中心X（175）を $P$ で表す。^[4]

$Pは$ $△$ $ABC$ の内心とジェルゴンヌ点を結ぶ線上にあります。
$P が$ フェルドカンプの意味で $△ ABC$ の等周点である場合、三角形 $△$ $PBC$ $、 △$ $PCA$ $、 △$ $PAB$ の外接円は互いに接し、 $P$ はそれらの根心です。
$P$ がVeldkampの意味で $△ ABC$ の等周点である場合、 $△ PBC 、△ PCA 、△ PAB$ の周長は次の式に等しい。

${\frac {2\triangle }{{\bigl |}4R+r-(a+b+c){\bigr |}}}$ ここで $△$ は面積、 $R$ は円周半径、 $r$ は内接半径、 $a、b、cは$ $△ ABC$ の辺の長さである。^[6]

ソディサークル

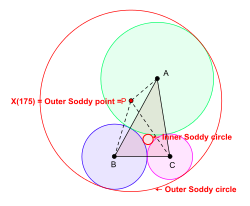
三角形 $△ ABC$ $が与えられているとき、 △ ABC$ の平面上に、 $A、 B、 C$ を中心とする円を描き、それらの円が互いに外部接するようにすることができる。一般に、 $A、 B、 C$ を中心とする3つの円にそれぞれ接するように2つの新しい円を描くことができる（円のうち1つは直線になることがある）。これらの円は $△$ $ABC$ のソディ円である。半径の小さい方の円は内側ソディ円であり、その中心は $△$ $ABC$ の内側ソディ点または内側ソディ中心と呼ばれる。半径の大きい方の円は外側ソディ円であり、その中心は三角形 $△$ $ABC$ の外側ソディ点または外側ソディ中心と呼ばれる。 ^[6]^[7]

三角形の中心X (175)は、キンバーリングの意味での等周点であり、 $△ ABC$ の外側のソディ点である。

参考文献

^ ab GR Veldkamp (1985). 「等周点と等迂回点」.アメリカ数学月刊誌. 92 (8): 546– 558. doi :10.2307/2323159. JSTOR 2323159.
^ Hajja, Mowaffaq; Yff, Peter (2007). 「三角形における等周点と等迂回点」. Journal of Geometry . 87 ( 1–2 ): 76– 82. doi :10.1007/s00022-007-1906-y. S2CID 122898960.
^ キンバリング、クラーク「等周点と等迂回点」2012年5月27日閲覧。
^ abc Kimberling, Clark. 「X(175) Isoperimetric Point」。2012年4月19日時点のオリジナルよりアーカイブ。2012年5月27日閲覧。
^ エミール・ルモワーヌの記事はガリカで閲覧できます。論文は111ページから始まり、126ページでこの点が論じられています。ガリカ
^ ab Nikolaos Dergiades (2007). "The Soddy Circles" (PDF) . Forum Geometricorum . 7 : 191–197 . 2010年6月14日時点のオリジナル(PDF)からアーカイブ。 2012年5月29日閲覧。
^ 「Soddy Circles」 . 2012年5月29日閲覧。

外部リンク

等周点と等迂回点 - Geogebratube のインタラクティブイラスト

[Veldkamp-1] GR Veldkamp (1985). 「等周点と等迂回点」.アメリカ数学月刊誌. 92 (8): 546– 558. doi :10.2307/2323159. JSTOR 2323159.

[2] Hajja, Mowaffaq; Yff, Peter (2007). 「三角形における等周点と等迂回点」. Journal of Geometry . 87 ( 1–2 ): 76– 82. doi :10.1007/s00022-007-1906-y. S2CID 122898960.

[3] キンバリング、クラーク「等周点と等迂回点」2012年5月27日閲覧。

[ETC-4] Kimberling, Clark. 「X(175) Isoperimetric Point」。2012年4月19日時点のオリジナルよりアーカイブ。2012年5月27日閲覧。

[5] エミール・ルモワーヌの記事はガリカで閲覧できます。論文は111ページから始まり、126ページでこの点が論じられています。ガリカ

[Dergi-6] Nikolaos Dergiades (2007). "The Soddy Circles" (PDF) . Forum Geometricorum . 7 : 191–197 . 2010年6月14日時点のオリジナル(PDF)からアーカイブ。 2012年5月29日閲覧。

[7] 「Soddy Circles」 . 2012年5月29日閲覧。