k平均法クラスタリング

k平均法クラスタリングはベクトル量子化の一手法であり、元々は信号処理から生まれたもので、 n個の観測値をk 個のクラスターに分割 し、各観測値が最も近い平均値（クラスター中心またはクラスター重心）を持つクラスターに属するようにします。これにより、データ空間がボロノイセルに分割されます。k平均法クラスタリングはクラスター内分散（二乗ユークリッド距離）を最小化しますが、通常のユークリッド距離は最小化しません。これはより困難なウェーバー問題です。平均値は二乗誤差を最適化しますが、幾何中央値のみがユークリッド距離を最小化します。例えば、 k中央値とkメドイドを用いることで、より良いユークリッド解を見つけることができます。

この問題は計算上困難（NP困難）ですが、効率的なヒューリスティックアルゴリズムによって局所最適解に速やかに収束します。これらのアルゴリズムは通常、 k平均法とガウス混合モデルの両方で用いられる反復改良法を介したガウス分布の混合に対する期待値最大化アルゴリズムに似ています。どちらもクラスター中心を用いてデータをモデル化しますが、k平均法クラスタリングは同程度の空間的広がりを持つクラスターを見つける傾向があるのに対し、ガウス混合モデルではクラスターの形状が異なっていても構いません。

教師なしk平均法アルゴリズムは、 k近傍分類器と緩い関係があります。k近傍分類器は、教師あり機械学習でよく使われる分類手法ですが、その名称からk平均法と混同されることがよくあります。k平均法によって得られたクラスター中心に1近傍分類器を適用すると、新しいデータが既存のクラスターに分類されます。これは、最近傍重心分類器またはロッキオアルゴリズムとして知られています。

説明

観測値の集合( x 1 , x 2 , ..., x n )が与えられ、各観測値は次元の実数ベクトルである場合、k平均クラスタリングは、 n 個の観測値をk ( ≤ n ) 個の集合S = { S 1 , S 2 , ..., S k }に分割して、クラスター内二乗和 (WCSS) (つまり、分散) を最小化することを目的とします。 正式には、この目的は次を見つけることです。 ここで、μ iは 内の点の平均 (重心とも呼ばれる) であり、 つまり のサイズであり、は通常のL 2ノルムです。 これは、同じクラスター内の点のペアワイズ二乗偏差を最小化することと同じです。 この 同等性は恒等式 から推測できます。 全体の分散は一定であるため、これは異なるクラスター内の点間の二乗偏差の合計(クラスター間二乗和、BCSS) を最大化することと同じです。[ 1 ]この決定論的な関係は、確率論における全分散の法則とも関連している。 d{\displaystyle d}argminS⁡∑i＝1k∑×∈Si‖×−μi‖2＝argminS⁡∑i＝1k|Si|変数⁡Si{\displaystyle \mathop {\operatorname {arg\,min} }_{\mathbf {S} }\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}=\mathop {\operatorname {arg\,min} }_{\mathbf {S} }\sum _{i=1}^{k}|S_{i}|\operatorname {Var} S_{i}}Si{\displaystyle S_{i}}μi＝1|Si|∑×∈Si×,{\displaystyle {\boldsymbol {\mu_{i}}}={\frac {1}{|S_{i}|}}\sum_{\mathbf{x}\in S_{i}}\mathbf{x},}|Si|{\displaystyle |S_{i}|}Si{\displaystyle S_{i}}‖⋅‖{\displaystyle \|\cdot \|}argminS⁡∑i＝1k1|Si|∑×,y∈Si‖×−y‖2{\displaystyle \mathop {\operatorname {arg\,min} } _{\mathbf {S} }\sum _{i=1}^{k}\,{\frac {1}{|S_{i}|}}\,\sum _{\mathbf {x} ,\mathbf {y} \in S_{i}}\left\|\mathbf {x} -\mathbf {y} \右\|^{2}}|Si|∑×∈Si‖×−μi‖2＝12∑×,y∈Si‖×−y‖2{\textstyle |S_{i}|\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}={\frac {1}{2}}\sum _{\mathbf {x} ,\mathbf {y} \in S_{i}}\left\|\mathbf {x} -\mathbf {y} \right\|^{2}}

歴史

「 k平均法」という用語は、1967年にジェームズ・マックイーンによって初めて使用されましたが[ 2 ] 、そのアイデアは1956年のヒューゴ・スタインハウスにまで遡ります。[ 3 ]標準アルゴリズムは、 1957年にベル研究所のスチュアート・ロイドによってパルス符号変調の技術として初めて提案されましたが、1982年まで論文として発表されませんでした。[ 4 ] 1965年にエドワード・W・フォーギーが本質的に同じ方法を発表したため、ロイド・フォーギーアルゴリズムと呼ばれることもあります。[ 5 ]

アルゴリズム

標準アルゴリズム（単純k平均法）

k平均法の収束

最も一般的なアルゴリズムは、反復的な改良手法を用いる。その普遍性から、「k平均法アルゴリズム」と呼ばれることが多い。特にコンピュータサイエンスの分野では、ロイドのアルゴリズムとも呼ばれる。より高速な代替手法が存在するため、「ナイーブk平均法」と呼ばれることもある。[ 6 ]

初期k平均集合m 1 (1) , ..., m k (1)（下記参照）が与えられた場合、アルゴリズムは2つのステップを交互に実行して進行する：[ 7 ]

  1. 割り当てステップ：各観測値を最も近い平均（重心）を持つクラスターに割り当てます。つまり、最小二乗ユークリッド距離を持つクラスターに割り当てます。[ 8 ] （数学的には、これは平均によって生成されたボロノイ図に従って観測値を分割することを意味します。）各観測値は、たとえ2つ以上の観測値に割り当てることができたとしても、正確に1つの観測値に割り当てられます。Si(t)={xp:‖xp−mi(t)‖2≤‖xp−mj(t)‖2 ∀j,1≤j≤k},{\displaystyle S_{i}^{(t)}=\left\{x_{p}:\left\|x_{p}-m_{i}^{(t)}\right\|^{2}\leq \left\|x_{p}-m_{j}^{(t)}\right\|^{2}\ \forall j,1\leq j\leq k\right\},}xp{\displaystyle x_{p}}S(t){\displaystyle S^{(t)}}
  2. 更新ステップ：各クラスターに割り当てられた観測値の平均（重心）を再計算します。これは再フィッティングとも呼ばれます。mi(t+1)=1|Si(t)|∑xj∈Si(t)xj{\displaystyle m_{i}^{(t+1)}={\frac {1}{\left|S_{i}^{(t)}\right|}}\sum _{x_{j}\in S_{i}^{(t)}}x_{j}}

k -means法の目的関数はWCSS（クラスター内平方和）です。各反復処理の後、WCSSは単調減少し、非負の単調減少列となります。これにより、k -means法は常に収束することが保証されますが、必ずしも大域的最適値に収束するとは限りません。

アルゴリズムは、割り当てが変化しなくなったとき、またはWCSSが安定したときに収束したとみなされます。このアルゴリズムは、最適なクラスター割り当てを見つけることを保証するものではありません。[ 9 ]

このアルゴリズムは、オブジェクトを距離に基づいて最も近いクラスターに割り当てるという形で提示されることが多い。ユークリッド距離（二乗）以外の距離関数を使用すると、アルゴリズムが収束しない可能性がある。球面k平均法やkメドイド法など、k平均法の様々な修正法が提案されており、他の距離尺度の使用を可能にする。

擬似コード

以下の擬似コードは、標準的なk平均法クラスタリングアルゴリズムの実装の概要を示しています。重心の初期化、点と重心間の距離、および新しい重心の計算は設計上の選択であり、実装によって異なります。この例の擬似コードでは、distance()指定された点間の距離を返します 

関数kmeans(k, points)は // 重心を初期化する 重心 ← k個の開始重心のリスト 収束 ← 偽 収束している間== false行う // 空のクラスターを作成する クラスター ← k個の空リストのリスト // 各点を最も近い重心に割り当てる i ← 0からlength(points) - 1まで実行します ポイント ← ポイント[i] 最も近いインデックス ← 0 minDistance ← 距離(点, 重心[0]) j ← 1からk - 1まで 、d ← distance (point, centroids[j]) を実行し、 d < minDistanceならば 最小距離 ← d 最も近いインデックス ← j クラスター[最も近いインデックス]。追加（ポイント） // 各クラスターの平均として重心を再計算します newCentroids ← 空のリスト i ← 0からk - 1まで 、newCentroid ← calculateCentroid (clusters[i])を実行します。 newCentroids. append (newCentroid) // 収束をチェックする newCentroids == centroidsの場合 収束 ← 真 そうでない場合 重心 ← 新しい重心 クラスター を返す

初期化法

一般的に用いられる初期化法は、フォーギー法とランダム分割法です。[ 10 ]フォーギー法は、データセットからk個の観測値をランダムに選択し、初期平均値として使用します。ランダム分割法は、まず各観測値にクラスターをランダムに割り当て、次に更新ステップに進み、クラスターにランダムに割り当てられた点の重心を初期平均値として計算します。フォーギー法は初期平均値を広げる傾向がありますが、ランダム分割法はすべての初期平均値をデータセットの中心近くに配置します。Hamerlyらによると、[ 10 ]ランダム分割法は、 k調和平均やファジーk平均法などのアルゴリズムには一般的に適しています。期待値最大化アルゴリズムや標準的なk平均法アルゴリズムには、フォーギー法による初期化が適していますしかし、 Celebiらによる包括的な研究[ 11 ]では、Forgy、Random Partition、Maximinなどの一般的な初期化方法のパフォーマンスが低いことが多いのに対し、BradleyとFayyadのアプローチ[ 12 ]は「最良のグループ」で「一貫して」パフォーマンスを発揮し、k -means++は「一般的に良好」なパフォーマンスを発揮することがわかりました。

  • 標準アルゴリズムのデモンストレーション
  • 1. k個の初期「平均」（この場合はk=3）がデータ領域（色で表示）内でランダムに生成されます
    1. k 個の初期「平均」（この場合はk =3）がデータ領域内でランダムに生成されます（色で表示）。
  • 2. 各観測値を最も近い平均値に関連付けることで、k個のクラスターが作成されます。ここでの区画は、平均値によって生成されたボロノイ図を表します。
    2.各観測値を最も近い平均値に関連付けることで、 k個のクラスターが作成されます。ここでの区画は、平均値によって生成されたボロノイ図を表します。
  • 3. k 個のクラスターそれぞれの重心が新しい平均になります。
    3. k個のクラスターそれぞれの重心が新しい平均になります。
  • 4. 収束に達するまで手順 2 と 3 を繰り返します。
    4. 収束に達するまで手順 2 と 3 を繰り返します。

このアルゴリズムは、大域的最適解への収束を保証するものではありません。結果は初期クラスターに依存する可能性があります。このアルゴリズムは通常高速であるため、異なる初期条件で複数回実行することが一般的です。しかし、最悪のケースではパフォーマンスが低下する可能性があります。特に、特定の点集合は、2次元であっても、指数時間、つまり2 Ω( n )で収束します。[ 13 ]これらの点集合は実際には発生しないようです。これは、 k平均法の平滑化実行時間が多項式であるという事実によって裏付けられています。[ 14 ]

「割り当て」ステップは「期待値ステップ」と呼ばれ、「更新ステップ」は最大化ステップであるため、このアルゴリズムは一般化期待値最大化アルゴリズムのバリエーションになります。

複雑性

d次元 の観測値に対するk平均法クラスタリング問題の最適解を求めることは、次の式で表されます

したがって、上記に示したロイドのアルゴリズムなどの さまざまなヒューリスティックアルゴリズムが一般的に使用されます。

ロイドのアルゴリズム（およびほとんどの変種）の実行時間は、[ 9 ] [ 19 ]であり、 O(nkdi){\displaystyle O(nkdi)}

  • nはd次元ベクトルの数（クラスター化される）
  • kクラスターの数
  • i収束までに必要な反復回数。

クラスタリング構造を持つデータでは、収束までの反復回数はしばしば少なく、最初の12回の反復を過ぎると結果の改善はわずかにしか見られません。そのため、ロイドのアルゴリズムは実際には「線形」な計算量を持つと考えられることが多いものの、収束まで実行すると最悪の場合、超多項式的な計算量になります。[ 20 ]

  • 最悪の場合、ロイドのアルゴリズムは反復を必要とするため、ロイドのアルゴリズムの最悪ケースの複雑さは超多項式となる。[ 20 ]i=2Ω(n){\displaystyle i=2^{\Omega ({\sqrt {n}})}}
  • ロイドのk平均法は、多項式平滑化実行時間を持つ。 [ 14 ]によれば、任意のn点集合において、各点が平均0、分散 の正規分布によって独立に摂動を受ける場合、 k平均法の期待実行時間はで制限される。これはn、k、d、の多項式である。[0,1]d{\displaystyle [0,1]^{d}}σ2{\displaystyle \sigma ^{2}}O(n34k34d8log4⁡(n)/σ6){\displaystyle O(n^{34}k^{34}d^{8}\log ^{4}(n)/\sigma ^{6})}1/σ{\displaystyle 1/\sigma }
  • 単純なケースでは、より良い境界が証明されています。例えば、k平均法アルゴリズムの実行時間は、整数格子内のn点に対して、 で制限されることが示されています。[ 21 ]O(dn4M2){\displaystyle O(dn^{4}M^{2})}{1,…,M}d{\displaystyle \{1,\dots ,M\}^{d}}

ロイドのアルゴリズムはこの問題に対する標準的なアプローチです。しかし、 k個のクラスター中心とn個のデータ点間の距離を計算するのに多くの処理時間がかかります。点は通常、数回の反復処理の後は同じクラスターに留まるため、この作業の多くは不要であり、単純な実装は非常に非効率的です。一部の実装では、キャッシュと三角不等式を用いて境界を作成し、ロイドのアルゴリズムを高速化しています。[ 22 ] [ 9 ] [ 23 ] [ 24 ] [ 25 ] [ 26 ]

最適なクラスター数

k平均法クラスタリングにおいて最適なクラスター数（k）を見つけることは、クラスタリング結果が有意義で有用なものとなるための重要なステップです。[ 27 ]適切なクラスター数を決定するための手法はいくつかあります。以下に、一般的に用いられる手法をいくつか示します。

  • エルボー法（クラスタリング）：この方法では、説明変数をクラスター数の関数としてプロットし、曲線のエルボーをクラスター数として選択します。[ 28 ]しかし、「エルボー」の概念は明確に定義されておらず、信頼性が低いことが知られています。[ 29 ]
  • シルエット（クラスタリング）：シルエット分析はクラスタリングの質を測定し、結果として得られるクラスター間の分離距離についての洞察を提供します。[ 30 ]シルエットスコアが高いほど、オブジェクトが自身のクラスターとはよく一致し、隣接するクラスターとは一致しにくいことを示します。
  • ギャップ統計：ギャップ統計は、異なるkの値に対するクラスター内変動の合計を、データのヌル参照分布の下での期待値と比較します。[ 31 ]最適なkは、最大のギャップ統計をもたらす値です。
  • デイヴィス・ボールディン指数：デイヴィス・ボールディン指数は、クラスター間の分離の程度を測る指標である。[ 32 ]デイヴィス・ボールディン指数の値が低いほど、分離が良好なモデルであることを示す。
  • Calinski-Harabasz指数：この指数は、クラスターのコンパクトさと分離度に基づいて評価します。この指数は、クラスター間の分散とクラスター内の分散の比を用いて計算され、値が高いほどクラスターが明確に定義されていることを示します。[ 33 ]
  • ランド指数：同じクラスターと異なるクラスターの両方に正しく割り当てられた要素のペアを考慮し、2つのクラスター間の一致率を計算します。[ 34 ]値が高いほど類似性が高く、クラスタリングの質が高いことを示します。より正確な指標を提供するために、1985年にHubertとArabieによって導入された調整ランド指数（ARI）は、偶然によるすべてのペアの期待類似性を調整することでランド指数を補正します。[ 35 ]

バリエーション

ハーティガン・ウォン法

ハーティガンとウォン法[ 9 ]は、 k平均法アルゴリズムのバリエーションであり、異なる解の更新を用いて最小二乗和問題の局所的最小値に向かって進みます。この方法は、目的関数が改善される限り、サンプルを別のクラスターに再配置しようと繰り返し試みる局所探索です。目的関数の改善を伴う別のクラスターに再配置できるサンプルがない場合、この方法は停止します（局所的最小値で）。古典的なk平均法と同様に、このアプローチは、最終解が必ずしも大域的最適解であることを保証するものではないため、ヒューリスティックな手法のままです

を の個別コストとし、 をクラスターの中心 として定義します。φ(Sj){\displaystyle \varphi (S_{j})}Sj{\displaystyle S_{j}}∑x∈Sj(x−μj)2{\textstyle \sum _{x\in S_{j}}(x-\mu _{j})^{2}}μj{\displaystyle \mu _{j}}

割り当てステップ
ハーティガンとウォンの方法は、点をランダムなクラスターに分割することから始まります{Sj}j∈{1,⋯k}{\displaystyle \{S_{j}\}_{j\in \{1,\cdots k\}}}
更新手順
次に、次の関数が最大値に達するおよびを決定します。この最大値に達するについては、クラスター からクラスター に移動します。n,m∈{1,…,k}{\displaystyle n,m\in \{1,\ldots ,k\}}x∈Sn{\displaystyle x\in S_{n}}Δ(m,n,x)=φ(Sn)+φ(Sm)−φ(Sn∖{x})−φ(Sm∪{x}).{\displaystyle \Delta (m,n,x)=\varphi (S_{n})+\varphi (S_{m})-\varphi (S_{n}\setminus \{x\})-\varphi (S_{m}\cup \{x\}).}x,n,m{\displaystyle x,n,m}x{\displaystyle x}Sn{\displaystyle S_{n}}Sm{\displaystyle S_{m}}
終了
アルゴリズムは、すべての に対して が 0 未満になると終了しますΔ(m,n,x){\displaystyle \Delta (m,n,x)}x,n,m{\displaystyle x,n,m}

様々な移動受入れ戦略が使用可能である。第一改善戦略では、改善可能なあらゆる再配置を適用できるが、最良改善戦略では、すべての可能な再配置が反復的にテストされ、各反復で最良のもののみが適用される。前者のアプローチは速度を重視し、後者のアプローチは一般的に追加の計算時間を犠牲にして解の品質を重視する。再配置の結果を計算するために使用される関数は、等式[ 45 ]を用いて効率的に評価することもできる。Δ{\displaystyle \Delta }

Δ(x,n,m)=∣Sn∣∣Sn∣−1⋅‖μn−x‖2−∣Sm∣∣Sm∣+1⋅‖μm−x‖2.{\displaystyle \Delta (x,n,m)={\frac {\mid S_{n}\mid }{\mid S_{n}\mid -1}}\cdot \lVert \mu _{n}-x\rVert ^{2}-{\frac {\mid S_{m}\mid }{\mid S_{m}\mid +1}}\cdot \lVert \mu _{m}-x\rVert ^{2}.}

グローバル最適化とメタヒューリスティックス

古典的なk平均法アルゴリズムとそのバリエーションは、次のように定義される最小二乗和クラスタリング問題の局所的最小値にのみ収束することが知られています。 多くの研究では、アルゴリズムの収束挙動を改善し、大域的最適値 (または少なくとも、より高品質の局所的最小値) を達成する可能性を最大化しようと試みられてきました。前のセクションで説明した初期化と再開のテクニックは、より良いソリューションを見つけるための 1 つの代替手段です。最近では、分岐限定計画法と半正定値計画法に基づく大域的最適化アルゴリズムにより、最大 4,177 のエンティティと 20,531 の特徴を持つデータセットに対して「証明済みの最適な」ソリューションが生成されました。[ 46 ]予想どおり、基礎となる最適化問題のNP 困難性により、 k平均法の最適アルゴリズムの計算時間は、このサイズを超えると急速に増加します。小規模および中規模の最適ソリューションは、他のヒューリスティックの品質を評価するためのベンチマーク ツールとして依然として価値があります。制御された計算時間内で最適性の保証なしに高品質の局所最小値を見つけるために、他の研究では、増分アプローチと凸最適化に基づくメタヒューリスティックスやその他のグローバル最適化手法、 [ 47 ]ランダムスワップ[ 48 ]（つまり、反復局所探索）、可変近傍探索[ 49 ] 、遺伝的アルゴリズム[ 50 ]などの手法が検討されてきました。[ 51 ]最小二乗和クラスタリング問題のより良い局所最小値を見つけることが、高次元の特徴空間におけるクラスター構造の回復の成功と失敗を分ける可能性があることは実際に知られています。[ 51 ]argminS⁡∑i=1k∑x∈Si‖x−μi‖2.{\displaystyle \mathop {\operatorname {arg\,min} } _{\mathbf {S} }\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}.}

考察

k -means法が局所最小値に収束する典型的な例。この例では、 k -meansクラスタリングの結果（右図）がデータセットの明らかなクラスター構造と矛盾しています。小さな円はデータポイント、4つの星印は重心（平均値）です。初期構成は左図に示されています。アルゴリズムは、図に左から右に示されている5回の反復後に収束します。この図はMirkes Javaアプレットを使用して作成されました。[ 52 ]
アイリスの花のデータセットと実際の種をELKIを用いて視覚化したk平均法クラスタリングの結果。クラスター平均は、より大きな半透明のシンボルで示されています。
人工データセット（「マウス」）におけるk平均法クラスタリングとEMクラスタリングの比較。k平均法は均一なサイズのクラスターを生成する傾向があるため、ここでは悪い結果につながりますが、EMはデータセット内に存在する異なる半径のガウス分布の恩恵を受けます。

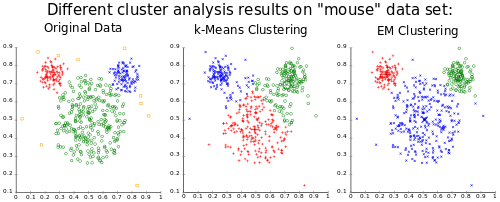
k平均法の効率性を高める 3 つの重要な特徴は、しばしば最大の欠点と見なされます。

  • ユークリッド距離はメトリックとして使用され、分散はクラスター散布の尺度として使用されます。
  • クラスター数kは入力パラメータです。kを適切に選択しないと、結果が悪くなる可能性があります。そのため、k平均法を実行する際には、データセット内のクラスター数を決定するための診断チェックを実行することが重要です。
  • 局所的最小値への収束により、直感に反する（「間違った」）結果が生成される場合があります（図の例を参照）。

k平均法の主な制限は、そのクラスター モデルにあります。この概念は、平均がクラスターの中心に向かって収束するように分離可能な球状クラスターに基づいています。クラスターは同様のサイズであることが期待されるため、最も近いクラスターの中心に割り当てるのが正しい割り当てになります。たとえば、 の値を持つk平均法を有名なアヤメのデータ セットに適用すると、結果ではデータ セットに含まれる 3種類のアヤメを分離できないことがよくあります。 を使用すると、目に見える 2 つのクラスター (1 つに 2 種類が含まれる) が検出されますが、 を使用すると、2 つのクラスターのうち 1 つが 2 つの均等な部分に分割されます。実際、データ セットには 3 つのクラスが含まれていますが、 の方がこのデータ セットに適しています。他のクラスタリング アルゴリズムと同様に、k平均法の結果では、データが特定の基準を満たしていると想定しています。これは一部のデータ セットではうまく機能しますが、他のデータ セットでは機能しません。 k=3{\displaystyle k=3}k=2{\displaystyle k=2}k=3{\displaystyle k=3}k=2{\displaystyle k=2}

k平均法の結果は、クラスター平均のボロノイセルとして見ることができます。データはクラスター平均の中間で分割されるため、「マウス」の例に見られるように、最適ではない分割につながる可能性があります。期待最大化アルゴリズム（ k平均法の一般化とも言える）で使用されるガウスモデルは、分散と共分散の両方を持つため、より柔軟です。したがって、EM法の結果は、k平均法よりもはるかに多くのサイズのクラスターや相関のあるクラスター（この例ではそうではありません）に対応できます。一方、EM法ではより多くの自由パラメータの最適化が必要であり、消失するクラスターや条件の悪い共分散行列のためにいくつかの方法論的な問題が生じます。k平均法は、ノンパラメトリックベイズモデリングと密接に関連しています。[ 53 ]

応用

k平均法クラスタリングは、特にロイドのアルゴリズムなどのヒューリスティックスを使用する場合、大規模なデータセットにも比較的簡単に適用できます。市場セグメンテーション、コンピュータービジョン、天文学など、多くの分野で効果的に使用されてきました。また、他のアルゴリズムの前処理ステップとして、例えば初期構成を見つけるためにもよく使用されます

ベクトル量子化

ベクトル量子化は、信号処理やコンピュータグラフィックスで一般的に使用される手法で、画像のカラーパレットをkと呼ばれる固定数の色に減らします。ベクトル量子化を実現するための一般的な方法の1つは、 k平均法クラスタリングです。このプロセスでは、k平均法を画像の色空間に適用してk個のクラスターに分割し、各クラスターは画像内の異なる色を表します。この手法は、画像セグメンテーションタスクで特に役立ち、類似した色を識別してグループ化するのに役立ちます

赤と緑のチャンネルのみを含むサンプル画像（説明目的）
上の画像に存在する色をk平均法を用いてボロノイセルにベクトル量子化する

例:コンピュータグラフィックスの分野では、画像圧縮における色量子化にk平均法がよく用いられます。画像を表現するために使用される色数を減らすことで、画質を大幅に損なうことなくファイルサイズを大幅に削減できます。たとえば、数百万色もの色がある画像を考えてみましょう。k を小さな数値に設定して k平均法クラスタリングを適用すると、より限定されたカラーパレットを使用して画像を表現できるため、圧縮されたバージョンではストレージ容量と帯域幅の消費量が少なくなります。ベクトル量子化のその他の用途としては、非ランダムサンプリングがあります。k 平均法を使用すれば、大規模なデータセットからk個の異なるが典型的なオブジェクトを簡単に選択して、さらに分析することができます。

クラスター分析

データマイニングと機械学習における基本的なタスクであるクラスター分析では、一連のデータポイントを類似性に基づいてクラスターにグループ化します。k平均法クラスタリングは、データをk個のクラスターに分割するために使用される一般的なアルゴリズムで、各クラスターはその重心で表されます

しかし、純粋なk平均法アルゴリズムは柔軟性に欠けるため、用途が限られています（前述のようなベクトル量子化が実際に望ましいユースケースである場合を除く）。特に、パラメータkは、外部制約によって与えられない場合、（前述のように）選択が困難であることが知られています。また、任意の距離関数や非数値データには使用できないという制限もあります。これらのユースケースでは、他の多くのアルゴリズムの方が優れています。

例：マーケティングにおいて、K平均法クラスタリングは市場セグメンテーションによく用いられます。市場セグメンテーションでは、類似した特性や行動を持つ顧客をグループ化します。例えば、小売企業はK平均法クラスタリングを用いて、購買行動、人口統計、地理的位置などの要因に基づいて顧客ベースを明確なグループに分割することができます。これらの顧客セグメントは、売上と顧客満足度を最大化するために、カスタマイズされたマーケティング戦略と製品提供によってターゲティングされます。

特徴学習

k平均法クラスタリングは、（半）教師あり学習または教師なし学習において、特徴学習（または辞書学習）ステップとして用いられてきた。[ 54 ]基本的なアプローチは、まず入力学習データ（ラベル付けは不要）を用いてk平均法クラスタリング表現を学習することである。次に、任意の入力データを新しい特徴空間に投影するために、「エンコード」関数（例えば、データと重心位置の閾値付き行列積など）を用いて、データから各重心までの距離を計算する。あるいは、単に最も近い重心を示す指標関数を用いることもできる。[ 54 ] [ 55 ]あるいは、距離を滑らかに変換する方法もある。[ 56 ]あるいは、サンプル-クラスター間距離をガウスRBFを用いて変換することで、ラジアル基底関数ネットワークの隠れ層を得ることができる。[ 57 ]

k平均法のこの使用法は、自然言語処理（NLP）（特に固有表現認識）[ 58 ]やコンピュータビジョンにおける半教師あり学習において、単純な線形分類器とうまく組み合わせられてきました。物体認識タスクでは、オートエンコーダや制限付きボルツマンマシンなどのより洗練された特徴学習手法と同等の性能を示すことが確認されています。[ 56 ]しかし、各データポイントは1つの「特徴」にしか寄与しないため、同等の性能を得るには一般的により多くのデータが必要になります。[ 54 ]

例：自然言語処理（NLP）において、k平均法クラスタリングは、固有表現抽出（NER）などの半教師あり学習タスクのための単純な線形分類器と統合されています。k平均法を用いてラベルなしテキストデータをクラスタリングすることで、意味のある特徴を抽出し、NERモデルの性能を向上させることができます。例えば、k平均法クラスタリングを適用することで、入力テキスト内で頻繁に共起する単語やフレーズのクラスターを識別し、それをNERモデルのトレーニング用の特徴として使用することができます。このアプローチは、ラベル付きデータに対する要件はより高くなりますが、 オートエンコーダや制限付きボルツマンマシンなどのより複雑な特徴学習手法と同等の性能を達成することが示されています。

最近の動向

k -meansクラスタリングの応用における最近の進歩には、k -means++初期化法を用いた、より効果的な初期クラスター重心の選択など、初期化手法の改良が含まれます。さらに、研究者たちは、コンピュータービジョン、自然言語処理、その他の分野における様々なタスクのパフォーマンス向上を目的として、 k -meansクラスタリングと畳み込みニューラルネットワーク（CNN）やリカレントニューラルネットワーク（RNN）などの深層学習手法の統合を研究しています。

他のアルゴリズムとの関係

ガウス混合モデル

k平均法クラスタリングのための低速な「標準アルゴリズム」と、それに関連する期待最大化アルゴリズムは、ガウス混合モデルの特殊なケース、具体的には、すべての共分散が対角で等しく、無限小の小さな分散を持つように固定した場合の極限ケースです。[ 59 ]：850 小さな分散の代わりに、ハードクラスター割り当てを使用して、k平均法クラスタリングと「ハード」ガウス混合モデリングの特殊なケースの別の同等性を示すこともできます。[ 60 ]：354、11.4.2.5 これは、k平均法を計算するためにガウス混合モデリングを使用することが効率的であることを意味するのではなく、理論的な関係があり、ガウス混合モデリングがk平均法の一般化として解釈できることを意味します逆に、k平均法クラスタリングを用いて、難しいデータに対するガウス混合モデリングの開始点を見つけることが提案されている。[ 59 ]：849

k -SVD

k-平均法アルゴリズムのもう1つの一般化はk -SVDアルゴリズムであり、これはデータ点を「コードブックベクトル」の疎な線形結合として推定します。k-平均法は、重みが1の単一のコードブックベクトルを使用する特殊なケースに対応します。[ 61 ]

主成分分析

クラスター指標で指定されるk平均法クラスタリングの緩和された解は、主成分分析 (PCA) によって与えられます。[ 62 ] [ 63 ] 直感的には、k平均法は球形 (ボールのような) のクラスターを表します。データに 2 つのクラスターがある場合、2 つの重心を結ぶ線が最適な 1 次元投影方向であり、これが PCA の最初の方向でもあります。線を質量の中心で切断すると、クラスターが分離します (これが離散クラスター指標の連続緩和です)。データに 3 つのクラスターがある場合、3 つのクラスター重心によって張られる 2 次元平面が最適な 2 次元投影です。この平面も、最初の 2 つの PCA 次元によって定義されます。十分に分離されたクラスターは、ボール型のクラスターによって効果的にモデル化されるため、k平均法によって検出されます。ボール型以外のクラスターは、近くにあると分離が困難です。例えば、空間的に絡み合った2つの半月形のクラスターは、PCAサブスペースに投影するとうまく分離しません。k平均法は、このデータではうまく機能するとは期待できません。[ 64 ]クラスターの重心サブスペースが主方向によって張られるという主張に対する反例を挙げるのは簡単です。[ 65 ]

平均シフトクラスタリング

基本的な平均シフト・クラスタリング・アルゴリズムは、入力データセットと同じサイズのデータ​​点の集合を維持します。最初に、この集合は入力集合からコピーされます。その後、すべての点は周囲の点の平均に向かって反復的に移動されます。対照的に、k平均法は、クラスターの集合をk個のクラスターに制限します。これは通常、入力データセットの点の数よりもはるかに少なく、前のクラスター内の、その点に他のどの点よりも重心に近いすべての点の平均を使用します（例：各更新点のボロノイ分割内）。k平均法に似た平均シフト・アルゴリズムは、尤度平均シフトと呼ばれ、置換対象の点の集合を、変化点の集合から所定の距離内にある入力集合内のすべての点の平均に置き換えます。[ 66 ] k平均法に対する平均シフト・クラスタリングの利点は、クラスターの数を決定するパラメーターがないため、データセット内の任意の数のクラスターを検出できることです。平均シフトはk平均法よりもはるかに遅くなる可能性があり、帯域幅パラメーターの選択も必要です

独立成分分析

スパース性仮定の下、入力データが白色化変換によって前処理されている場合、k -means法は線形独立成分分析（ICA）タスクの解を生成します。これは、 k -means法が特徴学習にうまく適用できることを説明するのに役立ちます。[ 67 ]

バイラテラルフィルタリング

k平均法は、入力データセットの順序は重要ではないと暗黙的に仮定します。バイラテラルフィルタは、平均値に繰り返し置き換えられるデータ点の集合を維持するという点で、 k平均法や平均値シフトに似ています。ただし、バイラテラルフィルタは、（カーネル重み付け）平均の計算を、入力データの順序が近い点のみを含むように制限します。[ 66 ]これにより、画像内のピクセルの空間配置が非常に重要である画像ノイズ除去などの問題に適用できます

類似の問題

クラスター関数を最小化する二乗誤差の集合には、 k-メドイドアルゴリズムも含まれます。これは、各クラスターの中心点を実際の点の1つに強制するアプローチです。 つまり、重心の代わりにメドイドを使用します

ソフトウェア実装

アルゴリズムの異なる実装ではパフォーマンスに違いが見られ、テストデータセットでは最速で10秒、最遅で25,988秒（約7時間）かかりました。[ 1 ]これらの違いは、実装の品質、言語とコンパイラの違い、終了基準と精度レベルの違い、加速のためのインデックスの使用に起因します

フリーソフトウェア／オープンソース

以下の実装は、フリー／オープンソースソフトウェアライセンスの下で利用可能であり、ソースコードは公開されています

  • Accord.NETには、 k -means、k -means++、k -modesの C# 実装が含まれています。
  • ALGLIBには、 k -means およびk- means++用の並列化された C++ および C# 実装が含まれています。
  • AOSP には、 k平均法の Java 実装が含まれています。
  • CrimeStat は2 つの空間k平均アルゴリズムを実装しており、そのうちの 1 つではユーザーが開始場所を定義できます。
  • ELKI には、 k平均法 (Lloyd および MacQueen 反復法、およびk平均法++ 初期化などのさまざまな初期化を含む) と、より高度なさまざまなクラスタリング アルゴリズムが含まれています。
  • Smile には、k平均法やその他のさまざまなアルゴリズムと結果の視覚化 (Java、Kotlin、Scala 用) が含まれています。
  • Julia には、JuliaStats Clustering パッケージにk平均法の実装が含まれています。
  • KNIMEには、 k平均法とkメドイドのノードが含まれています。
  • Mahout にはMapReduceベースのk平均法が含まれています。
  • mlpack にはk -meansの C++ 実装が含まれています。
  • Octave にはk平均法が含まれます。
  • OpenCV にはk平均法の実装が含まれています。
  • Orange には、 kの自動選択とクラスター シルエット スコアリングを備えたk平均法クラスタリングのコンポーネントが含まれています。
  • PSPPにはk平均法が含まれており、QUICK CLUSTER コマンドはデータセットに対してk平均法クラスタリングを実行します。
  • Rには 3 つのk平均法バリエーションが含まれています。
  • SciPyとscikit-learn には複数のk平均法の実装が含まれています。
  • Spark MLlib は分散k平均アルゴリズムを実装します。
  • Torch には、 k平均法クラスタリングを提供するunsupパッケージが含まれています。
  • Weka にはk平均法とx平均法が含まれています。

独自

以下の実装は独自のライセンス条項に基づいて利用可能であり、ソースコードが公開されていない可能性があります

参照

参考文献

  1. ^ a bクリーゲル、ハンス＝ペーター、シューベルト、アーサー、ジメク（2016年）。「実行時評価の（ブラック）アート：比較しているのはアルゴリズムか実装か？」知識と情報システム。52 （ 2 ）：341–378。doi：10.1007 /s10115-016-1004-2。ISSN 0219-1377。S2CID 40772241  
  2. ^ MacQueen, JB (1967).多変量観測の分類と解析のためのいくつかの方法. 数理統計と確率に関する第5回バークレーシンポジウム議事録. 第1巻. カリフォルニア大学出版局. pp.  281– 297. MR 0214227. Zbl 0214.46201 . 2009年4月7日閲覧.  
  3. ^シュタインハウス、ヒューゴ(1957). 「パーティーの資材部門」。ブル。アカド。ポロン。科学。（フランス語で）。4 (12): 801–804 . MR 0090073。Zbl 0079.16403。  
  4. ^ロイド、スチュアート・P. (1957). 「PCMにおける最小二乗量子化」.ベル電話研究所論文.ずっと後のジャーナルに掲載された論文：Lloyd, Stuart P. (1982). "Least squares quantization in PCM" (PDF) . IEEE Transactions on Information Theory . 28 (2): 129– 137. CiteSeerX 10.1.1.131.1338 . doi : 10.1109/TIT.1982.1056489 . S2CID 10833328. 2009年4月15日閲覧.  
  5. ^ Forgy, Edward W. (1965). 「多変量データのクラスター分析：分類の効率性と解釈可能性」.バイオメトリクス. 21 (3): 768– 769. JSTOR 2528559 . 
  6. ^ Pelleg, Dan; Moore, Andrew (1999). 「幾何学的推論による正確なk -meansアルゴリズムの高速化」 .第5回ACM SIGKDD国際会議「知識発見とデータマイニング」の議事録. サンディエゴ、カリフォルニア州、アメリカ合衆国: ACM Press. pp.  277– 281. doi : 10.1145/312129.312248 . ISBN 9781581131437. S2CID  13907420 .
  7. ^ MacKay, David (2003). 「第20章 推論タスクの例：クラスタリング」(PDF) .情報理論、推論、学習アルゴリズム. ケンブリッジ大学出版局. pp.  284– 292. ISBN 978-0-521-64298-9. MR  2012999 .
  8. ^平方根は単調関数なので、これも最小ユークリッド距離の割り当てです
  9. ^ a b c d e Hartigan, JA; Wong, MA (1979). 「アルゴリズムAS 136: k平均法クラスタリングアルゴリズム」.英国王立統計学会誌、シリーズC. 28 ( 1): 100–108 . JSTOR 2346830 . 
  10. ^ a b Hamerly, Greg; Elkan, Charles (2002). 「より優れたクラスタリングを見つけるk -meansアルゴリズムの代替法」 (PDF) .第11回国際情報・知識管理会議 (CIKM) 議事録.
  11. ^ Celebi, ME; Kingravi, HA; Vela, PA (2013). 「k -meansクラスタリングアルゴリズムの効率的な初期化方法の比較研究」. Expert Systems with Applications . 40 (1): 200– 210. arXiv : 1209.1960 . doi : 10.1016/j.eswa.2012.07.021 . S2CID 6954668 . 
  12. ^ Bradley, Paul S.; Fayyad, Usama M. (1998). 「k -Meansクラスタリングにおける初期点の改良」第15回国際機械学習会議議事録.
  13. ^ Vattani, A. (2011). 「k-means法は平面上でも指数関数的に多くの反復を必要とする」(PDF) .離散幾何学と計算幾何学. 45 (4): 596– 616. doi : 10.1007/s00454-011-9340-1 . S2CID 42683406 . 
  14. ^ a b Arthur, David; Manthey, B.; Roeglin, H. (2009). 「k-meansは多項式平滑化複雑度を持つ」.第50回コンピュータサイエンス基礎シンポジウム (FOCS) の議事録. arXiv : 0904.1113 .
  15. ^ Aloise, D.; Deshpande, A.; Hansen, P.; Popat, P. (2009). 「ユークリッド平方和クラスタリングのNP困難性」 .機械学習. 75 (2): 245– 249. doi : 10.1007/s10994-009-5103-0 .
  16. ^ Dasgupta, S.; Freund, Y. (2009年7月). 「ベクトル量子化のためのランダム射影木」. IEEE Transactions on Information Theory . 55 (7): 3229–42 . arXiv : 0805.1390 . Bibcode : 2009ITIT...55.3229D . doi : 10.1109/TIT.2009.2021326 . S2CID 666114 . 
  17. ^マハジャン, ミーナ; ニムボルカール, プラジャクタ; バラダラジャン, カストゥリ (2009). 「平面k-平均法問題はNP困難である」. WALCOM: アルゴリズムと計算. コンピュータサイエンス講義ノート. 第5431巻. pp.  274– 285. doi : 10.1007/978-3-642-00202-1_24 . ISBN 978-3-642-00201-4。
  18. ^稲葉 正之; 加藤 暢; 今井 秀夫 (1994).重み付きボロノイ図とランダム化の分散ベースk-クラスタリングへの応用.第10回ACM計算幾何学シンポジウム論文集. pp.  332–9 . doi : 10.1145 /177424.178042
  19. ^マニング、クリストファー D.;ラガヴァン、プラバーカール。シュッツェ、ハインリッヒ (2008)。情報検索の概要。ケンブリッジ大学出版局。ISBN 978-0521865715. OCLC  190786122 .
  20. ^ a b Arthur, David; Vassilvitskii, Sergei (2006-01-01). 「k -means法はどれくらい遅いのか？」.第22回計算幾何学シンポジウム議事録. SCG '06. ACM. pp.  144– 153. doi : 10.1145/1137856.1137880 . ISBN 978-1595933409. S2CID  3084311 .
  21. ^ Bhowmick, Abhishek (2009). 「 k -meansクラスタリングにおけるロイドのアルゴリズムの理論的分析」 (PDF) . 2015年12月8日時点のオリジナル(PDF)からのアーカイブこちらも参照してください。
  22. ^ Ding, Yufei; Zhao, Yue; Shen, Xipeng; Musuvathi, Madan; Mytkowiczyear, Todd. 「Yinyang K-Means：一貫した高速化を実現する従来のK-Meansの代替法」（PDF） .第32回国際機械学習会議（ICML）議事録.
  23. ^ a b Phillips, Steven J. (2002). 「K-Means法と関連クラスタリングアルゴリズムの高速化」. Mount, David M.; Stein, Clifford (編). 「K -Means法と関連クラスタリングアルゴリズムの高速化」. Lecture Notes in Computer Science. Vol. 2409. Springer. pp.  166– 177. doi : 10.1007/3-540-45643-0_13 . ISBN 978-3-540-43977-6。
  24. ^ a b Elkan, Charles (2003). 「三角不等式を用いたk平均法の高速化」(PDF) .第20回国際機械学習会議 (ICML) 議事録.
  25. ^ a b Hamerly, Greg (2010). 「K平均法をさらに高速化する」. 2010 SIAM International Conference on Data Mining の議事録. pp.  130– 140. doi : 10.1137/1.9781611972801.12 . ISBN 978-0-89871-703-7。
  26. ^ a b Hamerly, Greg; Drake, Jonathan (2015). 「K-Meansクラスタリングにおけるロイドのアルゴリズムの高速化」.パーティションクラスタリングアルゴリズム. pp.  41– 78. doi : 10.1007/978-3-319-09259-1_2 . ISBN 978-3-319-09258-4。
  27. ^ Abiodun M. Ikotun、Absalom E. Ezugwu、Laith Abualigah、Belal Abuhaija、Jia Heming、「K平均法クラスタリングアルゴリズム：包括的なレビュー、変異分析、そしてビッグデータ時代の進歩」、Information Sciences、第622巻、2023年、178～210ページ、ISSN 0020-0255、 https: //doi.org/10.1016/j.ins.2022.11.139
  28. ^ 276. doi:10.1007/BF02289263. S2CID 120467216.
  29. ^ Schubert, Erich (2023-06-22). 「k-meansにおけるエルボー基準の使用をやめ、代わりにクラスター数を選択する方法」ACM SIGKDD Explorations Newsletter. 25 (1): 36–42. arXiv:2212.12189. doi:10.1145/3606274.3606278. ISSN 1931-0145.
  30. ^ Peter J. Rousseeuw (1987). 「シルエット：クラスター分析の解釈と検証のためのグラフィカルな補助」. 計算・応用数学. 20: 53–65. doi:10.1016/0377-0427(87)90125-7.
  31. ^ Robert Tibshirani、Guenther Walther、Trevor Hastie (2001). 「ギャップ統計量を用いたデータセット内のクラスター数の推定」Journal of the Royal Statistical Society, Series B. 63 (2): 411–423. doi:10.1111/1467-9868.00293. S2CID 59738652.
  32. ^ Davies, David L.; Bouldin, Donald W. (1979). 「クラスター分離尺度」. IEEE Transactions on Pattern Analysis and Machine Intelligence. PAMI-1 (2): 224–227. doi:10.1109/TPAMI.1979.4766909. S2CID 13254783.
  33. ^ Caliński, Tadeusz; Harabasz, Jerzy (1974). 「クラスター分析のための樹状突起法」. Communications in Statistics. 3 (1): 1–27. doi:10.1080/03610927408827101.
  34. ^ WM Rand (1971). 「クラスタリング手法の評価のための客観的基準」. アメリカ統計学会誌. 66 (336). アメリカ統計学会誌: 846–850. doi:10.2307/2284239. JSTOR 2284239.
  35. ^ヒューバート、L.、アラビー、P. (1985)。ヒューバート、L.、アラビー、P. (1985)。パーティションを比較しています。分類ジャーナル、2(1)、193-218。 https://doi.org/10.1007/BF01908075
  36. ^ Kanungo, Tapas; Mount, David M .; Netanyahu, Nathan S .; Piatko, Christine D .; Silverman, Ruth; Wu, Angela Y. (2002). 「効率的なk -meansクラスタリングアルゴリズム：分析と実装」（PDF） . IEEE Transactions on Pattern Analysis and Machine Intelligence . 24 (7): 881– 892. Bibcode : 2002ITPAM..24..881K . doi : 10.1109/TPAMI.2002.1017616 . S2CID 12003435.オリジナル（ PDF）から2009年10月7日にアーカイブ。 2009年4月24日閲覧。 
  37. ^ Drake, Jonathan (2012). 「適応型距離境界を用いた高速k -means法」 (PDF) .第5回NIPS機械学習最適化ワークショップ, OPT2012 .
  38. ^ Dhillon, IS; Modha, DM (2001). 「クラスタリングを用いた大規模スパーステキストデータの概念分解」 .機械学習. 42 (1): 143– 175. doi : 10.1023/a:1007612920971 .
  39. ^スタインバッハ、M.; カリピス、G.; クマール、V. (2000). "「文書クラスタリング手法の比較」。KDDテキストマイニングワークショップ。400 （ 1）：525-526。
  40. ^ Pelleg, D.; & Moore, AW (2000年6月). 「 X -means:クラスター数の効率的な推定によるk -means法の拡張」ICML , Vol. 1
  41. ^ Hamerly, Greg; Elkan, Charles (2004). 「k-means法におけるkの学習」(PDF) .ニューラル情報処理システムの進歩. 16 : 281.
  42. ^ Amorim, RC; Mirkin, B. (2012). 「 k -Meansクラスタリングにおけるミンコフスキー計量、特徴重み付け、異常なクラスタ初期化」.パターン認識. 45 (3): 1061– 1075. doi : 10.1016/j.patcog.2011.08.012 .
  43. ^ Amorim, RC; Hennig, C. (2015). 「特徴再スケーリング係数を用いたノイズ特徴を含むデータセットにおけるクラスター数の回復」. Information Sciences . 324 : 126–145 . arXiv : 1602.06989 . doi : 10.1016/j.ins.2015.06.039 . S2CID 315803 . 
  44. ^ Sculley, David (2010). 「Webスケールk -meansクラスタリング」 .第19回国際ワールドワイドウェブ会議議事録. ACM. pp.  1177– 1178. 2016年12月21日閲覧。
  45. ^ Telgarsky, Matus. 「Hartigan法： Voronoiを使用しないk -meansクラスタリング」（PDF） .
  46. ^ベロニカ、ピッチャリ;スドーソ、アントニオ M.ヴィーゲレ、アンジェリカ (2022-03-28)。「SOS-SDP: 最小二乗和クラスタリングのための正確なソルバー」。INFORMS ジャーナル・オン・コンピューティング。34 (4 ) : 2144–2162。arXiv : 2104.11542 。土井：10.1287/ijoc.2022.1166。ISSN 1091-9856。S2CID 233388043。  
  47. ^ Bagirov, AM; Taheri, S.; Ugon, J. (2016). 「最小二乗和クラスタリング問題に対する非平滑DC計画法アプローチ」.パターン認識. 53 : 12–24 . Bibcode : 2016PatRe..53...12B . doi : 10.1016/j.patcog.2015.11.011 .
  48. ^ Fränti, Pasi (2018). 「ランダムスワップクラスタリングの効率」 . Journal of Big Data . 5 (1) 13: 1– 21. doi : 10.1186/s40537-018-0122-y .
  49. ^ Hansen, P.; Mladenovic, N. (2001). 「J-Means: 最小二乗和クラスタリングのための新しい局所探索ヒューリスティック」.パターン認識. 34 (2): 405– 413. Bibcode : 2001PatRe..34..405H . doi : 10.1016/S0031-3203(99)00216-2 .
  50. ^ Krishna, K.; Murty, MN (1999). 「遺伝的k-meansアルゴリズム」 . IEEE Transactions on Systems, Man, and Cyber​​netics - Part B: Cyber​​netics . 29 (3): 433– 439. doi : 10.1109/3477.764879 . PMID 18252317 . 
  51. ^ a b Gribel, Daniel; Vidal, Thibaut (2019). 「HG-means: 最小二乗和クラスタリングのためのスケーラブルなハイブリッドメタヒューリスティック」.パターン認識. 88 : 569–583 . arXiv : 1804.09813 . doi : 10.1016/j.patcog.2018.12.022 . S2CID 13746584 . 
  52. ^ Mirkes, EM 「K-means and k- medoids applet」 。 2016年1月2日閲覧。
  53. ^ Kulis, Brian; Jordan, Michael I. (2012-06-26). 「k -means法の再考：ベイズ非パラメトリック法による新しいアルゴリズム」（PDF） . ICML . Association for Computing Machinery. pp.  1131– 1138. ISBN 9781450312851。
  54. ^ a b c Coates, Adam; Ng, Andrew Y. (2012). 「k- means法による特徴表現の学習」(PDF) . Montavon, G.; Orr, GB; Müller, K.-R. (編). Neural Networks: Tricks of the Trade . Springer
  55. ^ Csurka, Gabriella; Dance, Christopher C.; Fan, Lixin; Willamowski, Jutta; Bray, Cédric (2004).バッグオブキーポイントを用いた視覚的分類(PDF) . ECCVワークショップ「コンピュータビジョンにおける統計学習」
  56. ^ a b Coates, Adam; Lee, Honglak; Ng, Andrew Y. (2011).教師なし特徴学習における単層ネットワークの分析(PDF) . 人工知能と統計に関する国際会議 (AISTATS). 2013年5月10日時点のオリジナル(PDF)からアーカイブ。
  57. ^ Schwenker, Friedhelm; Kestler, Hans A.; Palm, Günther (2001). 「ラジアル基底関数ネットワークの3つの学習フェーズ」.ニューラルネットワーク. 14 ( 4–5 ): 439– 458. CiteSeerX 10.1.1.109.312 . doi : 10.1016/s0893-6080(01)00027-2 . PMID 11411631 .  
  58. ^ Lin, Dekang; Wu, Xiaoyun (2009).識別学習のためのフレーズクラスタリング(PDF) . ACLとIJCNLPの年次会議. pp.  1030– 1038.
  59. ^ a b Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). 「第16.1節 ガウス混合モデルとk平均クラスタリング」 . Numerical Recipes: The Art of Scientific Computing (第3版). ニューヨーク (NY): Cambridge University Press. ISBN 978-0-521-88068-8。
  60. ^ケビン・P・マーフィー (2012).機械学習：確率論的視点. マサチューセッツ州ケンブリッジ: MIT出版. ISBN 978-0-262-30524-2. OCLC  810414751 .
  61. ^ Aharon, Michal ; Elad, Michael ; Bruckstein, Alfred (2006). 「K-SVD：スパース表現のための過剰完備辞書設計アルゴリズム」（PDF） . IEEE Transactions on Signal Processing . 54 (11): 4311. Bibcode : 2006ITSP...54.4311A . doi : 10.1109/TSP.2006.881199 . S2CID 7477309. 2019年12月2日にオリジナル（PDF）からアーカイブ。2019年12月2日閲覧 
  62. ^ Zha, Hongyuan; Ding, Chris; Gu, Ming; He, Xiaofeng; Simon, Horst D. (2001年12月). 「 k -meansクラスタリングにおけるスペクトル緩和」 (PDF) . Neural Information Processing Systems Vol.14 (NIPS 2001) : 1057– 1064.
  63. ^ Ding, Chris; He, Xiaofeng (2004年7月). 「主成分分析によるK-meansクラスタリング」(PDF) .国際機械学習会議 (ICML 2004) 論文集: 225–232 .
  64. ^ Drineas, Petros; Frieze, Alan M.; Kannan, Ravi; Vempala, Santosh; Vinay, Vishwanathan (2004). 「特異値分解による大規模グラフのクラスタリング」(PDF) .機械学習. 56 ( 1–3 ): 9–33 . doi : 10.1023/b:mach.0000033113.59016.96 . S2CID 5892850. 2012年8月2日閲覧. 
  65. ^ Cohen, Michael B.; Elder, Sam; Musco, Cameron; Musco, Christopher; Persu, Madalina (2014). 「k -meansクラスタリングと低ランク近似のための次元削減（付録B）」arXiv : 1410.6801 [ cs.DS ].
  66. ^ a b Little, Max A.; Jones, Nick S. (2011). 「区分定数信号からのノイズ除去のための一般化された手法とソルバー．I. 背景理論」．Proceedings of the Royal Society A．467 ( 2135 ): 3088– 3114．Bibcode : 2011RSPSA.467.3088L．doi : 10.1098 / rspa.2010.0671．PMC 3191861．PMID 22003312．  
  67. ^ Vinnikov, Alon; Shalev-Shwartz, Shai (2014). 「独立成分がスパースな場合のK平均法によるICAフィルタの回復」(PDF) .国際機械学習会議 (ICML 2014) の議事録.
「 https://en.wikipedia.org/w/index.php?title=K-means_clustering&oldid=1329361755」より取得