リル法

Lill法を用いて、4次方程式3 x ⁴ +13 x ³ +19 x ² +11 x +2の根-2、-1（重根）、-1/3を求めます。黒線分には長さ（方程式の係数）がラベル付けされており、最初の傾きがmで端点が同じである各色線は実根に対応します。

数学において、リル法は、任意の次数の一変数多項式の実根を視覚的に求める方法です。^{[ 1 ]}この方法は、オーストリアの技術者エドゥアルト・リルによって1867年に開発されました。 ^{[ 2 ]}リルは後に複素根の問題を論文で取り上げました。^{[ 3 ]}

リルの方法は、多項式の係数に等しい長さの直角をなす直線部分のパスを描くというものです。多項式の根は、始点と終点を結ぶ他の直角パスの傾きとして求められますが、そのパスの頂点は最初のパスの直線上に存在します。

方法の説明

3次多項式4 x ³ + 2 x ² − 2 x − 1の根 −1/2、 −1/ √ 2、 1/ √ 2を求め、負の係数と拡張された線分の扱い方を示します。色付きの線上に示される各数値は、その傾きの負数であり、したがって多項式の実根です。

この方法を用いるには、原点から始めて図を描きます。線分は、最初の係数の大きさだけ右に引かれます。係数が負の場合、線分は原点の左で終わります。最初の線分の端から、2番目の係数の大きさだけ上向きに線分が引かれ、次に3番目の係数の大きさだけ左に引かれ、次に4番目の係数の大きさだけ下向きに引かれ、というように続きます。方向の順序（回転ではなく）は常に右向き、上向き、左向き、下向きで、これを繰り返します。したがって、各回転は反時計回りです。このプロセスは、ゼロを含む多項式のすべての係数に対して続けられ、負の係数は「逆方向に」進みます。方程式の定数項に対応する線分の端にある最終点が終点です。

次に、直線が原点から角度θで発射され、各線分で直角に反射され（必ずしも「自然な」反射角ではない）、角度のついた経路が線分に当たらない場合は、各線分（零係数の線を含む）を通る直線で直角に屈折します。[ ^{4 ]垂直}線と水平線は、次の順序で反射または屈折します。x ^{n −1}の係数に対応する線分を含む直線、次にx ^{n −2}の係数に対応する線分を含む直線などです。経路が終点に到達するようにθを選択すると、 −tan( θ )はこの多項式の根になります。多項式のすべての実数零点に対して、終点に到達する一意の初期角度と経路が1つ存在します。たとえば、2つの実根を持つ二次方程式は、上記の条件を満たす角度がちょうど2つあります。

複素根の場合も、相似三角形の連続体を見つける必要があるが、根の経路の頂点は多項式経路から根の虚数部に等しい距離だけずれている。この場合、根の経路は直角ではない。^{[ 5 ] [ 3 ]}

説明

この構成は、実際にはホーナー法に従って多項式を評価するものである。多項式 の場合、 、、 、…の値は、多項式経路の頂点と根の経路との間の距離として順次生成される。多項式の根の場合、最終値はゼロであるため、最後の頂点は多項式経路の終点と一致する。 ${\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots }$ ${\displaystyle a_{n}x}$ ${\displaystyle (a_{n}x+a_{n-1})x}$ ${\displaystyle ((a_{n}x+a_{n-1})x+a_{n-2})x}$

追加のプロパティ

根を与える解線は、その根が除去された多項式の Lill 構成に似ています。これは、視覚的な構成が、線形 (根)モニック(ルフィニの規則)による多項式の合成除算に類似しているためです。

図の対称性から、逆多項式の根は元の根の 逆数であることが簡単にわかります。

構築は、反時計回りの回転ではなく時計回りの回転を用いて行うこともできます。他の規則を用いて経路を解釈する場合、それは鏡映多項式（すべての奇数係数の符号が反転）に対応し、根は反転されます。

直角経路を同じ方向の規則で反対方向に横断すると、それは反転した鏡映多項式に対応し、根は元の根の負の逆数になります。^{[ 4 ]}

タレスの定理を用いた二次根の求め方

3 x ² + 5 x − 2の根を求める

リルの方法は、タレスの定理と組み合わせて使用​​して、二次多項式の実根を求めることができます。

3 x ² + 5 x − 2の例では、多項式の線分は上記のようにまず黒で描かれます。そして、始点と終点を結ぶ直線が直径を形成する円が描かれます。

タレスの定理によれば、これらの点と円上の他の任意の点を含む三角形は直角三角形です。この円とリル法の中線（必要に応じて延長）の交点が、リル法における2つの角度付きパス（青と赤）を定義します。

最初の線分の勾配の負の値mは、実根1/3と−2を生成します。

折り紙で根を見つける

3 x ³ + 2 x ² − 7 x + 2の根を求めよ

1936年、マルゲリータ・ピアッツォラ・ベロチは、リルの方法を応用して紙を折ることによって三次方程式を解く方法を示した。^{[ 6 ]}同時折りが許されれば、実根を持つn次方程式はn − 2回の同時折りで解くことができる。^{[ 7 ]}

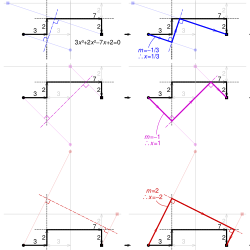
3 x ³ + 2 x ² − 7 x + 2の例では、まず多項式の線分を紙（黒）に描きます。2番目と3番目の線分の始点と終点の鏡映線（薄い円と四角形）を通る線と、それらに平行な線（灰色の線）を描きます。

それぞれの根について、紙を折り曲げ、始点（黒丸）と終点（黒四角）がこれらの直線に反射するまで折ります。反射軸（一点鎖線）は、根（青、紫、赤）に対応する角度のついた経路を定義します。これらの最初の線分の勾配の負の値mは、実根1/3、1、-2となります。

参照

• カーライル円は、ノルム二次関数に対するリル法をわずかに修正したものに基づいています。

参考文献

1. ダン・カルマン (2009). 『異例の数学的遠足：多項式と関連領域』 AMS. pp.  13–22 . ISBN 978-0-88385-341-2。
2. ME リル (1867)。「継続的に継続するための数値的グラフの解決、および機器の発明に関する説明」(PDF)。Nouvelles Annales de Mathématiques。 2. 6 : 359–362。
3. M. E. リル (1868)。「Résolution graphic des équations algébriques qui ont des racines imaginaires」(PDF)。Nouvelles Annales de Mathématiques。 2. 7 : 363–367 .
4. Bradford, Phillips Verner. 「直角幾何学的パスを用いたn次代数方程式の解の視覚化」 www.concentric.net. 2010年5月2日時点のオリジナルよりアーカイブ。 2012年2月3日閲覧。
5. Tabachnikov, Serge (2017-03-01). 「多項式を多角形として」(PDF) . The Mathematical Intelligencer . 39 (1): 41– 43. doi : 10.1007/s00283-016-9681-y . ISSN 1866-7414 . S2CID 126072703 .  
6. Thomas C. Hull (2011年4月). 「折り目を使った立方方程式の解法：ベロックとリルの研究」(PDF) . American Mathematical Monthly . 118 (4): 307– 315. doi : 10.4169/amer.math.monthly.118.04.307 . S2CID 2540978 . 
7. Roger C. Alperin; Robert J. Lang (2009). 「One-, Two-, and Multi-Fold Origami Axioms」（PDF） . 4OSME . AK Peters.オリジナル（PDF）から2022年2月13日にアーカイブ。 2012年4月20日閲覧。

外部リンク

• リルメソッドのアニメーション
• Mathologer のビデオ:「レーザーでカメを撃って方程式を解く」