初等幾何学の公式一覧

これは、一般的な数学的形状と図形、およびそれらを説明する公式の短いリストです。

2次元形状

形	エリア	周囲長	記号の意味
四角	${\displaystyle l^{2}}$	${\displaystyle 4l}$	${\displaystyle l}$ 辺の長さです
矩形	${\displaystyle lb}$	${\displaystyle 2(l+b)}$	${\displaystyle l}$ 長さは幅です ${\displaystyle b}$
丸	${\displaystyle \pi r^{2}}$	${\displaystyle 2\pi r}$ または${\displaystyle \pi d}$	は半径、は直径です ${\displaystyle r}$ ${\displaystyle d}$
楕円	${\displaystyle \pi ab}$		は長半径、は短半径である。${\displaystyle a}$ ${\displaystyle b}$
三角形	${\displaystyle {\frac {bh}{2}}}$	${\displaystyle a+b+c}$	${\displaystyle b}$ は底辺、は高さ、は辺 ${\displaystyle h}$ ${\displaystyle a,b,c}$
平行四辺形	${\displaystyle bh}$	${\displaystyle 2(a+b)}$	${\displaystyle b}$ 底辺、高さ、辺 ${\displaystyle h}$ ${\displaystyle a}$
台形	${\displaystyle {\frac {a+b}{2}}h}$		${\displaystyle a}$ そして、ベースは ${\displaystyle b}$

出典: ^{[ 1 ] [ 2 ] [ 3 ]}

立体形状

図形の方程式の項の図解

キューブ

直方体

プリズム

平行六面体

ピラミッド

四面体

円錐

シリンダー

球

楕円

これは基本的な図形の体積公式の一覧である: ^{[ 4 ] : 405–406}

• 円錐– 、ここでは底辺の半径、は円錐の高さです。${\textstyle {\frac {1}{3}}\pi r^{2}h}$ ${\textstyle r}$ ${\textstyle h}$
• 立方体– 、ここでは辺の長さです。${\textstyle a^{3}}$ ${\textstyle a}$
• 直方体– 、ここで、、、はそれぞれ辺の長さです。${\textstyle abc}$ ${\textstyle a}$ ${\textstyle b}$ ${\textstyle c}$
• 円柱– 、ここでは底辺の半径、は円柱の高さです。${\textstyle \pi r^{2}h}$ ${\textstyle r}$ ${\textstyle h}$
• 楕円体– 、ここで、、、およびは、長半径と短半径の長さです。${\textstyle {\frac {4}{3}}\pi abc}$ ${\textstyle a}$ ${\textstyle b}$ ${\textstyle c}$
• 球– 、ここで半径は;${\textstyle {\frac {4}{3}}\pi r^{3}}$ ${\textstyle r}$
• 平行六面体– 、ここで、、、およびは各辺の長さ、、、、およびは2辺間の角度です。${\textstyle abc{\sqrt {K}}}$ ${\textstyle a}$ ${\textstyle b}$ ${\textstyle c}$ ${\textstyle K=1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}$ ${\textstyle \alpha }$ ${\textstyle \beta }$ ${\textstyle \gamma }$
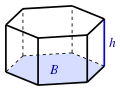
• プリズム– 、ここでは底面積、はプリズムの高さです。${\textstyle Bh}$ ${\textstyle B}$ ${\textstyle h}$
• ピラミッド– 、ここでは底面積、ピラミッドの高さです。${\textstyle {\frac {1}{3}}Bh}$ ${\textstyle B}$ ${\textstyle h}$
• 四面体– 、ここでは辺の長さです。${\textstyle {{\sqrt {2}} \over 12}a^{3}}$ ${\textstyle a}$

球

球面（2次元球面、3次元空間内の2次元面）を記述する基本量は、次の変数で表される。

• ${\displaystyle r}$ 半径は
• ${\displaystyle C=2\pi r}$ 円周（大円のいずれかの長さ）
• ${\displaystyle S}$ は表面積であり、
• ${\displaystyle V}$ ボリュームです。

表面積:

$${\displaystyle {\begin{alignedat}{4}S&=4\pi r^{2}\\[0.3ex]&={\frac {1}{\pi }}C^{2}\\[0.3ex]&={\sqrt[{3}]{\pi (6V)^{2}}}\\[0.3ex]\end{alignedat}}}$$

音量：

$${\displaystyle {\begin{alignedat}{4}V&={\frac {4}{3}}\pi r^{3}\\[0.3ex]&={\frac {1}{6\pi ^{2}}}C^{3}\\[0.3ex]&={\frac {1}{6{\sqrt {\pi }}}}S^{3/2}\\[0.3ex]\end{alignedat}}}$$

半径:

$${\displaystyle {\begin{alignedat}{4}r&={\frac {1}{2\pi }}C\\[0.3ex]&={\sqrt {{\frac {1}{4\pi }}S}}\\[0.3ex]&={\sqrt[{3}]{{\frac {3}{4\pi }}V}}\\[0.3ex]\end{alignedat}}}$$

円周:

$${\displaystyle {\begin{alignedat}{4}C&=2\pi r\\[0.3ex]&={\sqrt {\pi S}}\\[0.3ex]&={\sqrt[{3}]{\pi ^{2}6V}}\\[0.3ex]\end{alignedat}}}$$

参照

• 弧長 – 曲線に沿った距離
• 面積#面積の公式 – 2次元面の大きさ
• 周囲長#公式 – 領域を囲むパス
• 面積の2次モーメントの一覧
• 表面積と体積の比率の一覧 – 単位体積あたりの表面積
• 表面積の公式一覧 – 2次元表面の測定
• 三角関数の恒等式の一覧
• 体積公式一覧 – 三次元空間の量

参考文献

1. 「アーカイブコピー」（PDF） 。 2012年8月13日時点のオリジナル（PDF）からアーカイブ。 2011年11月29日閲覧。
2. 「面積の公式」。
3. 「基本的な幾何学の公式一覧」 2018年5月27日。
4. Treese, Steven A. (2018).基本単位と組立単位の歴史と測定. シャム, スイス: Springer Science+Business Media . ISBN 978-3-319-77577-7. LCCN  2018940415 . OCLC  1036766223 .