マクスウェル・ボルツマン統計

マクスウェル・ボルツマン統計は、理想気体中の粒子速度のマクスウェル・ボルツマン分布を導くために用いることができます。図： -100℃、20℃、600℃における10 ^{6 個の}酸素分子の速度分布。

統計力学において、マクスウェル・ボルツマン統計は、熱平衡状態における古典物質粒子の様々なエネルギー状態における分布を記述する。これは、温度が十分に高い場合、または粒子密​​度が十分に低く、量子効果が無視できる場合に適用できる。

マクスウェル・ボルツマン統計における エネルギーを持つ粒子の期待数は、 次のとおりです。 ${\displaystyle \varepsilon _{i}}$ $${\displaystyle \langle N_{i}\rangle ={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}}}={\frac {N}{Z}}\,g_{i}e^{-\varepsilon _{i}/k_{\text{B}}T},}$$

• ${\displaystyle \varepsilon _{i}}$ はi番目のエネルギーレベルのエネルギーであり、
• ${\displaystyle \langle N_{i}\rangle }$ はエネルギーを持つ状態の集合内の粒子の平均数であり、${\displaystyle \varepsilon _{i}}$
• ${\displaystyle g_{i}}$ はエネルギーレベルiの縮退、つまり、他の何らかの手段によって互いに区別できるエネルギーを持つ状態の数である。 ^[注1]${\displaystyle \varepsilon _{i}}$
• μは化学ポテンシャルであり、
• k _Bはボルツマン定数であり、
• Tは絶対温度、
• Nは粒子の総数である：、${\displaystyle \textstyle N=\sum _{i}N_{i}}$
• Zは分割関数である：、${\displaystyle \textstyle Z=\sum _{i}g_{i}e^{-\varepsilon _{i}/k_{\text{B}}T}}$
• eはオイラー数である

同様に、粒子の数は と表現されることもあります。 ここで、インデックスiは、エネルギー、を持つすべての状態の集合ではなく、特定の状態を指定します。 $${\displaystyle \langle N_{i}\rangle ={\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}}}={\frac {N}{Z}}\,e^{-\varepsilon _{i}/k_{\text{B}}T},}$$ ${\displaystyle \varepsilon _{i}}$ ${\textstyle Z=\sum _{i}e^{-\varepsilon _{i}/k_{\text{B}}T}}$

歴史

マクスウェル・ボルツマン統計は、マクスウェル・ボルツマン分布から派生したもので、おそらく基礎となる手法の抽出として生まれた。^{[疑わしい–議論が必要]}この分布は、1860年にマクスウェルによって経験的根拠に基づいて初めて導出された。その後、1870年代にボルツマンは、この分布の物理的起源について重要な研究を行った。この分布は、系のエントロピーを最大化するという根拠に基づいて導出できる。

マクスウェル・ボルツマン分布との関係

マクスウェル・ボルツマン分布とマクスウェル・ボルツマン統計は密接に関連しています。マクスウェル・ボルツマン統計は、統計力学におけるより一般的な原理であり、古典粒子が特定のエネルギー状態にある確率を記述します。 ここで、 $${\displaystyle P_{i}={\frac {e^{-E_{i}/k_{\text{B}}T}}{Z}}}$$

• ${\displaystyle Z}$ は分割関数である：、${\displaystyle \textstyle Z=\sum _{i}e^{-E_{i}/k_{\text{B}}T}}$
• ${\displaystyle E_{i}}$ 状態のエネルギーであり、${\displaystyle i}$
• ${\displaystyle k_{\text{B}}}$ ボルツマン定数である。
• ${\displaystyle T}$ 絶対温度です。

マクスウェル・ボルツマン分布は、マクスウェル・ボルツマン統計を気体粒子の運動エネルギーに応用したものです。理想気体中の粒子の速度分布は、気体分子のエネルギー準位はその運動エネルギーによって与えられるという統計的仮定から成ります。 ここで、 $${\displaystyle f(v)=\left({\frac {m}{2\pi k_{\text{B}}T}}\right)^{3/2}4\pi v^{2}e^{-{\frac {mv^{2}}{2k_{\text{B}}T}}}}$$

• ${\displaystyle f(v)}$ は粒子速度の確率密度関数であり、
• ${\displaystyle m}$ 粒子の質量である。
• ${\displaystyle k_{\text{B}}}$ ボルツマン定数である。
• ${\displaystyle T}$ 絶対温度です。
• ${\displaystyle v}$ 粒子の速度です。

導出

マクスウェル・ボルツマン分布は、エネルギー状態のマクスウェル・ボルツマン確率から始めて、運動エネルギーを代入して速度に関する確率を表現することで、 マクスウェル・ボルツマン統計から推測することができます。${\displaystyle E={\tfrac {1}{2}}mv^{2}}$ $${\displaystyle {\begin{aligned}P(E)&={\frac {1}{Z}}~\exp \left({\frac {-E}{k_{\text{B}}T}}\right)\\\rightarrow P(v)&={\frac {1}{Z}}~\exp \left({\frac {-mv^{2}}{2k_{\text{B}}T}}\right)\end{aligned}}}$$

3次元では、これは球の表面積に比例します。したがって、速度の確率密度関数（PDF）は次のようになります。 ${\displaystyle 4\pi v^{2}}$ ${\displaystyle v}$ $${\displaystyle f(v)=C\cdot 4\pi v^{2}\exp \left(-{\frac {mv^{2}}{2k_{\text{B}}T}}\right)}$$

正規化定数を求めるには、すべての可能な速度にわたる確率密度関数の積分が1になる必要があります。 ${\displaystyle C}$ $${\displaystyle {\begin{aligned}\int _{0}^{\infty }f(v)\,dv&=1\\\rightarrow C\int _{0}^{\infty }4\pi v^{2}\exp \left(-{\frac {mv^{2}}{2k_{\text{B}}T}}\right)dv&=1\end{aligned}}}$$

既知の結果 を使って積分を評価すると、次の式が得られます。 ${\displaystyle \int _{0}^{\infty }v^{2}e^{-av^{2}}dv={\frac {\sqrt {\pi }}{4a^{3/2}}}}$ ${\displaystyle a={\frac {m}{2k_{\text{B}}T}}}$ $${\displaystyle {\begin{aligned}C\cdot 4\pi \cdot {\frac {\sqrt {\pi }}{4\left({\frac {m}{2k_{\text{B}}T}}\right)^{3/2}}}=1\quad \rightarrow C=\left({\frac {m}{2\pi k_{\text{B}}T}}\right)^{3/2}\end{aligned}}}$$

したがって、マクスウェル・ボルツマンの速度分布は次のようになります。 $${\displaystyle f(v)=\left({\frac {m}{2\pi k_{\text{B}}T}}\right)^{3/2}4\pi v^{2}\exp \left(-{\frac {mv^{2}}{2k_{\text{B}}T}}\right)}$$

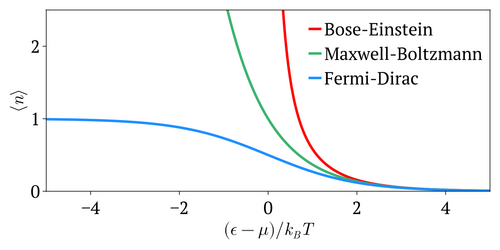
適用範囲

整数スピン（ボソン）、半整数スピン（フェルミオン）、および古典スピン（スピンレス）粒子の平衡熱分布。平均占有率は、系の化学ポテンシャルに対するエネルギーに対して示されている。ここで、は系の温度、はボルツマン定数である。${\displaystyle \langle n\rangle }$ ${\displaystyle \epsilon }$ ${\displaystyle \mu }$ ${\displaystyle T}$ ${\displaystyle k_{\text{B}}}$

マクスウェル・ボルツマン統計は、理想気体のマクスウェル・ボルツマン分布を導くために使用されます。しかし、この分布を、相対論的粒子（結果としてマクスウェル・ユットナー分布となる）など、異なるエネルギー・運動量関係を持つ粒子や、3次元空間以外の空間 に拡張するためにも使用できます。

マクスウェル・ボルツマン統計は、しばしば「区別可能な」古典粒子の統計として説明されます。言い換えれば、粒子Aが状態1にあり粒子Bが状態2にある場合の構成は、粒子Bが状態1にあり粒子Aが状態2にある場合とは異なります。この仮定は、エネルギー状態における粒子の適切な（ボルツマン）統計をもたらしますが、ギブスのパラドックスに体現されるように、エントロピーに関しては非物理的な結果をもたらします。

同時に、マクスウェル・ボルツマン統計が要求する特性を持つ粒子は実在しません。実際、特定の種類の粒子（例えば、電子、陽子など）をすべて原理的に区別できないものとして扱えば、ギブスのパラドックスは解決されます。この仮定が置かれると、粒子の統計は変化します。混合エントロピーの例におけるエントロピーの変化は、混合される2種類の粒子が区別可能であることから生じる非示量的エントロピーの例と見なすことができます。

量子粒子は、ボソン（ボーズ＝アインシュタイン統計に従う）またはフェルミオン（パウリの排他原理に従うが、フェルミ＝ディラック統計に従う）のいずれかである。これらの量子統計はどちらも、高温・低粒子密度の極限においてマクスウェル＝ボルツマン統計に近づく。

派生

マクスウェル・ボルツマン統計は、様々な統計力学的熱力学集団から導出することができる。^[1]

• まさに、グランドカノニカルアンサンブル。
• まさに、正統派のアンサンブルです。
• ミクロカノニカル集団ですが、熱力学的限界のみです。

いずれの場合も、粒子は相互作用せず、複数の粒子が同じ状態を占めることができ、独立してそうすることができると仮定する必要があります。

ミクロカノニカルアンサンブルからの導出

質量や電荷など、すべて同一の物理的特性を持つ非常に小さな粒子が多数入った容器があるとします。これをシステムと呼びましょう。粒子は同一の特性を持ちますが、互いに区別できるものとします。例えば、粒子の軌道を継続的に観察したり、宝くじの玉 のようにそれぞれ異なる数字を記すなど、粒子に印を付けることで、それぞれの粒子を識別することができます。

容器内の粒子はあらゆる方向に猛スピードで運動しています。粒子は高速で運動しているため、ある程度のエネルギーを持っています。マクスウェル・ボルツマン分布は、容器内の粒子のうち、どの程度の粒子が特定のエネルギーを持っているかを表す数学関数です。より正確には、マクスウェル・ボルツマン分布は、特定のエネルギーに対応する状態が占有される非正規化確率（つまり、確率の合計が1にならない確率）を与えます。

一般に、同じ量のエネルギー を持つ粒子が多数存在することがあります。同じエネルギーを持つ粒子の数を 、別のエネルギーを持つ粒子の数を とし、すべての可能なエネルギー について以下同様にします。この状況を説明するために、 はエネルギー レベルの占有数であると言います。占有数がすべて分かれば、システムの合計エネルギーがわかります。ただし、各エネルギー レベルをどの粒子が占有しているかを区別できるため、占有数の集合はシステムの状態を完全には説明しません。システムの状態、つまりミクロ状態を完全に説明するには、各エネルギー レベルにどの粒子があるのか​​を正確に指定する必要があります。したがって、システムの可能な状態の数を数えるときは、占有数の可能な集合だけでなく、すべてのミクロ状態を数えなければなりません。 ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon _{1}}$ ${\displaystyle N_{1}}$ ${\displaystyle \varepsilon _{2}}$ ${\displaystyle N_{2}}$ ${\displaystyle \{\varepsilon _{i}\mid i=1,2,3,\ldots \}}$ ${\displaystyle N_{i}}$ ${\displaystyle i.}$ ${\displaystyle \{N_{i}\mid i=1,2,3,\ldots \}}$ ${\displaystyle \{N_{i}\mid i=1,2,3,\ldots \}}$

まず、各エネルギー準位には状態が1つしかない（縮退がない）と仮定します。次に、粒子の貯蔵庫を正確に記述することにはほとんど関係のない、組み合わせ論的な考え方を少し扱います。例えば、 というラベルの付いた箱が全部で 個あるとします。組み合わせという概念を用いると、各箱の中のボールの順序が追跡されない場合に、箱の集合に何通りの配置方法があるかを計算できます。まず、箱 に入れるボールを全部で 個の中から選び、各箱について残りのボールから選び続け、すべてのボールがいずれかの箱に入るようにします。ボールを並べられる方法の総数は ${\displaystyle i}$ ${\displaystyle k}$ ${\displaystyle a,b,\ldots ,k}$ ${\displaystyle N}$ ${\displaystyle N_{a}}$ ${\displaystyle N}$ ${\displaystyle a}$ $${\displaystyle {\begin{aligned}W&={\frac {N!}{N_{a}!{\cancel {(N-N_{a})!}}}}\times {\frac {\cancel {(N-N_{a})!}}{N_{b}!{\cancel {(N-N_{a}-N_{b})!}}}}\times {\frac {\cancel {(N-N_{a}-N_{b})!}}{N_{c}!{\cancel {(N-N_{a}-N_{b}-N_{c})!}}}}\times \cdots \times {\frac {\cancel {(N-\cdots -N_{\ell })!}}{N_{k}!(N-\cdots -N_{\ell }-N_{k})!}}\\[8pt]&={\frac {N!}{N_{a}!N_{b}!N_{c}!\cdots N_{k}!(N-N_{a}-\cdots -N_{\ell }-N_{k})!}}\end{aligned}}}$$

すべてのボールが箱の中に入れられているので、式は次のように簡略化される。 ${\displaystyle (N-N_{a}-N_{b}-\cdots -N_{k})!=0!=1}$ $${\displaystyle W=N!\prod _{\ell =a,b,\ldots }^{k}{\frac {1}{N_{\ell }!}}}$$

これは単なる多項式係数、つまり、 N 個のアイテムをk 個のボックスに配置する方法の数です。l番目のボックスにはN _{l 個の}アイテムが格納され、各ボックス内のアイテムの順列は無視されます。

さて、箱の中に粒子を入れる方法が複数ある場合（つまり、縮退問題を考慮した場合）を考えてみましょう。番目の箱が の「縮退」、つまり「サブボックス」（同じエネルギーを持つ箱。同じエネルギーを持つこれらの状態/箱は縮退状態と呼ばれます）を持ち、サブボックスの数字を変えて番目の箱を埋める方法はどれも、箱を埋める異なる方法である場合、i番目の箱を埋める方法の数は、 「サブボックス」に物体を配置する方法の数だけ増加する必要があります。区別可能な物体を「サブボックス」に配置する方法の数は です（最初の物体はどの箱にも入れることができ、2番目の物体もどの箱にも入れることができ、以下同様です）。したがって、 i番目のレベルに粒子が収容されるような異なる状態を持つ各レベルにおいて、合計 の粒子をエネルギーに応じてエネルギー準位に分類できる方法の数は、次のようになります。 ${\displaystyle N_{i}}$ ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle N_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle N_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}^{N_{i}}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle W}$ ${\displaystyle N}$ ${\displaystyle i}$ ${\displaystyle g_{i}}$ ${\displaystyle N_{i}}$ $${\displaystyle W=N!\prod _{i}{\frac {g_{i}^{N_{i}}}{N_{i}!}}}$$

これは、ボルツマンによって初めて導かれたWの形である。ボルツマンの基本方程式は、熱力学的エントロピーSとミクロ状態の数Wを関連付ける。ここで、k _Bはボルツマン定数である。しかし、ギブスは、上記のWの式は広がりのあるエントロピーをもたらさず、したがって誤りであると指摘した。この問題は、ギブスのパラドックスとして知られている。問題は、上記の式で考慮される粒子が区別できないわけではないということである。言い換えると、2 つのエネルギー サブレベルの 2 つの粒子 ( AとB ) の場合、[ A、B ]で表される集団は、集団 [ B、A ]とは別個であると考えられるが、区別できない粒子の場合は別個ではない。区別できない粒子についての議論を進めると、Wのボーズ-アインシュタインの式が得られる。 ${\displaystyle S=k_{\text{B}}\,\ln W}$ $${\displaystyle W=\prod _{i}{\frac {(N_{i}+g_{i}-1)!}{N_{i}!(g_{i}-1)!}}}$$

絶対零度よりはるかに高い温度では、このボーズ・アインシュタイン分布からマクスウェル・ボルツマン分布が導かれ、 となる。マクスウェル・ボルツマン分布では密度が低いことも求められるため、 となる。これらの条件下では、階乗に対する スターリング近似を用いて次のよう に書ける。 ${\displaystyle g_{i}\gg 1}$ ${\displaystyle g_{i}\gg N_{i}}$ $${\displaystyle N!\approx N^{N}e^{-N},}$$ $${\displaystyle {\begin{aligned}W&=\prod _{i}{\frac {g_{i}}{N_{i}+g_{i}}}{\frac {(N_{i}+g_{i})!}{N_{i}!g_{i}!}}\approx \prod _{i}{\frac {(N_{i}+g_{i})!}{N_{i}!g_{i}!}}\\&\approx \prod _{i}{\frac {(N_{i}+g_{i})^{N_{i}+g_{i}}e^{-N_{i}-g_{i}}}{N_{i}!g_{i}^{g_{i}}e^{-g_{i}}}}=\prod _{i}{\frac {g_{i}^{N_{i}}(1+N_{i}/g_{i})^{N_{i}+g_{i}}e^{-N_{i}}}{N_{i}!}}\end{aligned}}}$$

事実を利用して、次のようになります。 ${\displaystyle (1+N_{i}/g_{i})^{N_{i}+g_{i}}\approx e^{N_{i}}}$ ${\displaystyle g_{i}\gg N_{i}}$ $${\displaystyle W\approx \prod _{i}{\frac {g_{i}^{N_{i}}}{N_{i}!}}}$$

これは本質的にはボルツマンのWの元の表現をNで割ったものであり、この補正は次のように呼ばれる。正しいボルツマンカウント。

容器内の粒子数とエネルギーは一定であるという制約を考慮しつつ、関数が最大化されるを求めたい。との最大値は、 との値が等しいときに達成されるが、数学的に実現する方が簡単なので、後者の関数を最大化することにする。関数を形成する ラグランジュ乗数を用いて、解を制約する。${\displaystyle N_{i}}$ ${\displaystyle W}$ ${\textstyle \left(N=\sum N_{i}\right)}$ ${\textstyle \left(E=\sum N_{i}\varepsilon _{i}\right)}$ ${\displaystyle W}$ ${\displaystyle \ln(W)}$ ${\displaystyle N_{i}}$ $${\displaystyle f(N_{1},N_{2},\ldots ,N_{n})=\textstyle \ln(W)+\alpha (N-\sum _{i}N_{i})+\beta (E-\sum _{i}N_{i}\varepsilon _{i})}$$ $${\displaystyle \ln W=\ln \left[\prod _{i=1}^{n}{\frac {g_{i}^{N_{i}}}{N_{i}!}}\right]\approx \sum _{i=1}^{n}\left(N_{i}\ln g_{i}-N_{i}\ln N_{i}+N_{i}\right)}$$

ついに $${\displaystyle f(N_{1},N_{2},\ldots ,N_{n})=\alpha N+\beta E+\sum _{i=1}^{n}\left[N_{i}\ln g_{i}-N_{i}\ln N_{i}+N_{i}-\left(\alpha +\beta \varepsilon _{i}\right)N_{i}\right]}$$

上記の式を最大化するために、フェルマーの定理（停留点）を適用します。これによれば、局所的極値が存在する場合は、臨界点（偏微分がゼロ）にある必要があります。 $${\displaystyle {\frac {\partial f}{\partial N_{i}}}=\ln g_{i}-\ln N_{i}-(\alpha +\beta \varepsilon _{i})=0}$$

上記の方程式（）を解くと、 の式が得られます。 ${\displaystyle i=1\ldots n}$ ${\displaystyle N_{i}}$ $${\displaystyle N_{i}={\frac {g_{i}}{e^{\alpha +\beta \varepsilon _{i}}}}}$$

この式をの式に代入し、 と仮定すると次の式が得られます。 または、整理すると次の式が得られます。 ${\displaystyle N_{i}}$ ${\displaystyle \ln W}$ ${\displaystyle N\gg 1}$ $${\displaystyle \ln W=(\alpha +1)N+\beta E\,}$$ $${\displaystyle E={\frac {\ln W}{\beta }}-{\frac {N}{\beta }}-{\frac {\alpha N}{\beta }}}$$

ボルツマンは、これが熱力学のオイラー積分基本方程式の単なる表現に過ぎないことに気づきました。Eを内部エネルギーとすると、オイラー積分基本方程式は次のように述べられます。 ここで、 Tは温度、Pは圧力、Vは体積、μは化学ポテンシャルです。ボルツマン方程式は、エントロピーがボルツマン定数を比例定数として表現したものです。理想気体の状態方程式（PV  =  Nk _B T）を用いると、すぐに次の式が成り立ち、したがって、各集団は次のように書き表すことができます。 $${\displaystyle E=TS-PV+\mu N}$$ ${\displaystyle S=k_{\text{B}}\ln W}$ ${\displaystyle \ln W}$ ${\displaystyle \beta =1/k_{\text{B}}T}$ ${\displaystyle \alpha =-\mu /k_{\text{B}}T}$ $${\displaystyle N_{i}={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/(k_{\text{B}}T)}}}}$$

上記の式は、 絶対活性と表記されることも あることに注意してください。 $${\displaystyle N_{i}={\frac {g_{i}}{e^{\varepsilon _{i}/k_{\text{B}}T}/z}}}$$ ${\displaystyle z=\exp(\mu /k_{\text{B}}T)}$

あるいは、次の事実を利用して 人口数を求める こともできます。 ここで、Z は次のように定義されるパーティション関数です。$${\displaystyle \sum _{i}N_{i}=N}$$ $${\displaystyle N_{i}=N{\frac {g_{i}e^{-\varepsilon _{i}/k_{\text{B}}T}}{Z}}}$$ $${\displaystyle Z=\sum _{i}g_{i}e^{-\varepsilon _{i}/k_{\text{B}}T}}$$

ε _iが連続変数であると考えられる近似では、トーマス・フェルミ近似はに比例する連続的な退化gを生じ、次の式が成り立ちます。 これはエネルギーの マクスウェル・ボルツマン分布そのものです。${\displaystyle {\sqrt {\varepsilon }}}$ $${\displaystyle {\frac {{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{\int _{0}^{\infty }{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}}={\frac {{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{{\frac {\sqrt {\pi }}{2}}(k_{\text{B}}T)^{3/2}}}={\frac {2{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{\sqrt {\pi (k_{\text{B}}T)^{3}}}}}$$

標準アンサンブルからの導出

上述の議論では、ボルツマン分布関数は系の多重度を直接解析することによって得られました。あるいは、正準アンサンブルを利用することもできます。正準アンサンブルでは、系は熱的にリザーバーと接触しています。エネルギーは系とリザーバーの間で自由に流れますが、リザーバーは結合系全体の 温度Tを一定に保つために、無限に大きな熱容量を持つと考えられます。

本稿では、系は縮退したエネルギー準位を持つと仮定する。前回と同様に、系がエネルギーを持つ確率を計算したい。 ${\displaystyle \varepsilon _{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle \varepsilon _{i}}$

システムが状態 にある場合、リザーバーには対応する数のミクロ状態が存在する。この数を と呼ぶ。仮定により、結合システム（関心のあるシステムとリザーバー）は孤立しているため、すべてのミクロ状態は等確率で発生する。したがって、例えば の場合、システムが状態 にある可能性はの2倍であると結論付けることができる。一般に、がシステムが状態 にある確率である場合、 ${\displaystyle s_{1}}$ ${\displaystyle \Omega _{\text{R}}(s_{1})}$ ${\displaystyle \Omega _{\text{R}}(s_{1})=2\;\Omega _{\text{R}}(s_{2})}$ ${\displaystyle s_{1}}$ ${\displaystyle s_{2}}$ ${\displaystyle P(s_{i})}$ ${\displaystyle s_{i}}$ $${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {\Omega _{\text{R}}(s_{1})}{\Omega _{\text{R}}(s_{2})}}.}$$

貯水池の エントロピーは${\displaystyle S_{\text{R}}=k\ln \Omega _{\text{R}}}$ $${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {e^{S_{\text{R}}(s_{1})/k}}{e^{S_{\text{R}}(s_{2})/k}}}=e^{(S_{\text{R}}(s_{1})-S_{\text{R}}(s_{2}))/k}.}$$

次に、熱力学の恒等式を思い出します（熱力学の第一法則と第二法則から）。 $${\displaystyle dS_{\text{R}}={\frac {1}{T}}(dU_{\text{R}}+P\,dV_{\text{R}}-\mu \,dN_{\text{R}}).}$$

正準集団では粒子の交換は行われないため、項はゼロになります。同様に、 です。これは となります。 ここで、 と はそれぞれ、における貯蔵庫とシステムのエネルギーを表します。2番目の等式については、エネルギー保存則を用いました。 を と に関する最初の式に代入すると、 系の 任意の 状態sに対して、 となります。 ここで、 Zは全確率が1になるように適切に選ばれた「定数」です。（温度Tが不変 であれば、 Zは定数です。） ここで、添え字sは系のすべてのミクロ状態を通ります。Zは、状態全体のボルツマン和（または元のドイツ語では「Zustandssumme」）と呼ばれることもあります。総和をすべての可能な状態ではなくエネルギー固有値で添え字付けする場合、縮退を考慮する必要があります。系がエネルギーを持つ確率は、対応するすべてのミクロ状態の確率の和に単純化されます。 ここで、明らかな修正を加えると、 これは以前と同じ結果になります。 ${\displaystyle dN_{\text{R}}}$ ${\displaystyle dV_{\text{R}}=0}$ $${\displaystyle S_{\text{R}}(s_{1})-S_{\text{R}}(s_{2})={\frac {1}{T}}(U_{\text{R}}(s_{1})-U_{\text{R}}(s_{2}))=-{\frac {1}{T}}(E(s_{1})-E(s_{2})),}$$ ${\displaystyle U_{\text{R}}(s_{i})}$ ${\displaystyle E(s_{i})}$ ${\displaystyle s_{i}}$ ${\displaystyle P(s_{1}),\;P(s_{2})}$ $${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {e^{-E(s_{1})/k_{\text{B}}T}}{e^{-E(s_{2})/k_{\text{B}}T}}},}$$ $${\displaystyle P(s)={\frac {1}{Z}}e^{-E(s)/k_{\text{B}}T},}$$ $${\displaystyle Z=\sum _{s}e^{-E(s)/k_{\text{B}}T},}$$ ${\displaystyle \varepsilon _{i}}$ $${\displaystyle P(\varepsilon _{i})={\frac {1}{Z}}g_{i}e^{-\varepsilon _{i}/k_{\text{B}}T}}$$ $${\displaystyle Z=\sum _{j}g_{j}e^{-\varepsilon _{j}/k_{\text{B}}T},}$$

この導出に関するコメント:

• この定式化では、「…系には合計N個の粒子があると仮定する…」という最初の仮定  が省略されていることに注意してください。実際、系が保有する粒子の数は分布の導出に何ら影響を与えません。むしろ、エネルギーを持つ状態を何個の粒子が占めるかが、容易に導き出されます。${\displaystyle \varepsilon _{i}}$
• 上記は本質的には正準分配関数の導出です。定義を比較すればわかるように、状態間のボルツマン和は正準分配関数に等しくなります。
• フェルミ・ディラック統計とボーズ・アインシュタイン統計を導くのにも全く同じアプローチが使えます。しかし、系とリザーバーの間で粒子の交換が行われるため、カノニカル集団をグランドカノニカル集団に置き換える必要があります。また、これらのケースで考慮する系は粒子ではなく、単一粒子状態です。（上記の議論では、系を単一原子と仮定することもできました。）

標準アンサンブルからの導出

マクスウェル・ボルツマン分布は、古典系において粒子がエネルギー状態Eを占める確率を記述する。これは以下の形をとる。 $${\displaystyle {\begin{aligned}f_{\text{MB,high}}(E)&=\exp \left(-{\frac {E-E_{\text{F}}}{k_{\text{B}}T}}\right),&{\text{for }}E\gg E_{\text{F}}\\f_{\text{MB,low}}(E)&=1-\exp \left({\frac {E-E_{\text{F}}}{k_{\text{B}}T}}\right),&{\text{for }}E\ll E_{\text{F}}\end{aligned}}}$$

区別できない粒子のシステムの場合、標準集団形式から始めます。

エネルギー準位 を持つ系において、状態iにある粒子の数を とします。全エネルギーと粒子数は以下の通りです。 ${\displaystyle \{E_{i}\}}$ ${\displaystyle n_{i}}$ $${\displaystyle {\begin{aligned}E_{\text{total}}&=\sum _{i}n_{i}E_{i}\\N&=\sum _{i}n_{i}\end{aligned}}}$$

特定の構成の場合、標準集団内の確率は次のようになります。 ${\displaystyle \{n_{i}\}}$ $${\displaystyle P(\{n_{i}\})={\frac {1}{Z_{N}}}{\frac {N!}{\prod _{i}n_{i}!}}\prod _{i}(e^{-\beta E_{i}})^{n_{i}}}$$

この係数は、 N 個の区別できない粒子を状態間で 分配する方法の数を表します。${\displaystyle {\frac {N!}{\prod _{i}n_{i}!}}}$

マクスウェル・ボルツマン統計では、任意の状態の平均占有数が 1 ( ) よりはるかに小さいと仮定します。これは次の式に当てはまります。 ここで、は によって決定される化学ポテンシャルです。 ${\displaystyle \langle n_{i}\rangle \ll 1}$ $${\displaystyle \langle n_{i}\rangle \approx e^{-\beta (E_{i}-\mu )}}$$ ${\displaystyle \mu }$ ${\displaystyle \textstyle \sum _{i}\langle n_{i}\rangle =N}$

フェルミエネルギー に近いエネルギー状態の場合、 と表すことができ、次のようになります。 ${\displaystyle E_{\text{F}}}$ ${\displaystyle \mu \approx E_{\text{F}}}$ $${\displaystyle f_{\text{MB}}(E)=e^{-(E-E_{\text{F}})/k_{\text{B}}T}}$$

高エネルギー（）の場合、これは直接的に次式を与えます： ${\displaystyle E\gg E_{\text{F}}}$ $${\displaystyle f_{\text{MB,high}}(E)=e^{-(E-E_{\text{F}})/k_{\text{B}}T}}$$

低エネルギー（ ）の場合、小さいxに対する近似値を使用します。 ${\displaystyle E\ll E_{\text{F}}}$ ${\displaystyle e^{-x}\approx 1-x}$ $${\displaystyle f_{\text{MB,low}}(E)\approx 1-e^{(E-E_{\text{F}})/k_{\text{B}}T}}$$

これは、両方のエネルギー領域におけるマクスウェル・ボルツマン分布の導出です。

参照

• ボーズ・アインシュタイン統計
• フェルミ・ディラック統計
• ボルツマン因子

注記

1. 例えば、2つの単純な点粒子は同じエネルギーを持つが、異なる運動量ベクトルを持つ場合があります。この基準に基づいて、それらは互いに区別することができ、縮退とは、それらを区別できる可能性のある方法の数です。

参考文献

1. トールマン, RC (1938). 『統計力学の原理』ドーバー出版. ISBN 9780486638966。

参考文献

• カーター、アシュリー H.、「古典的および統計的熱力学」、Prentice–Hall、Inc.、2001 年、ニュージャージー。
• Raj Pathria、「統計力学」、Butterworth–Heinemann、1996年。