最小偏差

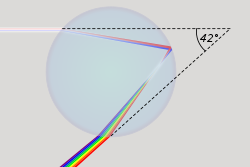
Condition when the angle of deviation is minimal in a prism

プリズムにおいて、偏角（ $δ$ ）は入射角（ $i$ ）の増加とともに、ある特定の角度まで減少します。プリズムにおける偏角が最小となる入射角は、プリズムの最小偏角位置と呼ばれ、その偏角は最小偏角（ $δ min$ 、 $D λ$ 、または $D m$ で表される）として知られています。

最小偏向角は屈折率と次のように関係します。

$n_{21}={\dfrac {\sin \left({\dfrac {A+D_{m}}{2}}\right)}{\sin \left({\dfrac {A}{2}}\right)}}$

これは物質の屈折率を計算するのに役立ちます。虹やハローは最小偏角で発生します。また、薄いプリズムは常に最小偏角に設定されます。

式

最小偏角では、プリズム内で屈折した光線はプリズムの底面と平行になります。言い換えれば、光線はプリズムの対称軸を中心に対称です。^[1]^[2]^[3] また、屈折角は等しく、 $r 1 = r 2$ です。入射角と出射角は互いに等しくなります（ $i = e$ ）。これは下のグラフで明確に示されています。

最小偏角の公式は、プリズムの幾何学的性質を利用することで導き出すことができます。このアプローチでは、上記の特性を利用して、スネルの法則における変数を偏角とプリズム角に置き換えます。

の角度の和から、 ${\textstyle \triangle OPQ}$

$A+\angle OPQ+\angle OQP=180^{\circ }$ $\implies A=180^{\circ }-(90-r)-(90-r)$ $\implies r={\frac {A}{2}}$

の外角定理を用いると、 ${\textstyle \triangle PQR}$

$D_{m}=\angle RPQ+\angle RQP$ $\implies D_{m}=i-r+i-r$ $\implies 2r+D_{m}=2i$ $\implies A+D_{m}=2i$ $\implies i={\frac {A+D_{m}}{2}}$

これはプリズムの式に $i = e$ を代入することによっても導かれる： $i + e = A + δ$

スネルの法則から、

$n_{21}={\dfrac {\sin i}{\sin r}}$

$\therefore n_{21}={\dfrac {\sin \left({\dfrac {A+D_{m}}{2}}\right)}{\sin \left({\dfrac {A}{2}}\right)}}$ ^[4]^[3]^[1]^[2]^[5]^{[過剰な引用]}

$\therefore D_{m}=2\sin ^{-1}\left(n\sin \left({\frac {A}{2}}\right)\right)-A$

(ここで、 $n$ は屈折率、 $A$ はプリズム角、 $D m$ は最小偏角です。)

これは、物質（液体または気体）の屈折率を測定するのに便利な方法であり、物質を満たしたプリズムまたは物質に浸したガラスプリズムに、無視できる厚さのプリズムを通して光線を最小の偏差で照射することによって測定する。^[5]^[3]^[1]

実行例:

ガラスの屈折率は1.5です。正角プリズムの最小偏角とそれに対応する入射角が求められます。

答え: 37°、49°

解決：

ここで、 $A = 60°$ 、 $n = 1.5$

上記の式に代入すると、

${\textstyle {\frac {\sin \left({\frac {60+\delta }{2}}\right)}{\sin \left({\frac {60}{2}}\right)}}=1.5}$

${\textstyle \implies {\frac {\sin \left(30+{\frac {\delta }{2}}\right)}{\sin(30)}}=1.5}$

${\textstyle \implies \sin \left(30+{\frac {\delta }{2}}\right)=1.5\times 0.5}$

${\textstyle \implies 30+{\frac {\delta }{2}}=\sin ^{-1}(0.75)}$

${\textstyle \implies {\frac {\delta }{2}}=48.6-30}$

${\textstyle \implies \delta =2\times 18.6}$

${\textstyle \therefore \delta \approx 37^{\circ }}$

また、

${\textstyle i={\frac {(A+\delta )}{2}}={\frac {60+2\times 18.6}{2}}\approx 49^{\circ }}$

これは以下のグラフでも明らかです。

屈折率 1.4 のプリズムの最小偏角がその屈折角に等しい場合、プリズムの角度は望ましいものとなります。

答え：60°

解決：

ここ、 ${\textstyle \delta =r}$

${\textstyle \implies \delta ={\frac {A}{2}}}$

上記の式を用いると、

${\textstyle {\frac {\sin \left({\frac {A+{\frac {A}{2}}}{2}}\right)}{\sin \left({\frac {A}{2}}\right)}}=1.4}$

${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\frac {1}{2}}{\frac {1}{\sqrt {2}}}}}$

${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\sin 45^{\circ }}{\sin 30^{\circ }}}}$

${\textstyle \therefore A=60^{\circ }}$

また、任意の入射角による偏角の変化は、スネルの法則を用いたプリズムの式で δ を $iで表すことによって、1 つの式にまとめることができます。$

$\delta =i-A+\sin ^{-1}\left(n\cdot \sin \left(A-\sin ^{-1}\left({\frac {\sin i}{n}}\right)\right)\right)=f(i)$

この方程式の最小値を見つけると、上記と同じ最小偏差の関係も得られます。

を置くと、 $f'(i)=0$

${\frac {\cos \left(A-\sin ^{-1}\left({\frac {\sin i}{u}}\right)\right)\cos i}{\sqrt {\left(1-u^{2}\sin ^{2}\left(A-\sin ^{-1}\left({\frac {\sin i}{u}}\right)\right)\right)\left(1-{\frac {\sin ^{2}i}{u^{2}}}\right)}}}=1$ この式を解くことで、プリズムの角度が特定の値である場合の入射角の値と、最小偏角が得られるプリズムの相対屈折率の値を得ることができます。式と説明は以下に記載されています。

薄型プリズム用

薄いプリズムや小角度プリズムでは、角度が非常に小さくなると、角度の正弦が角度自体にほぼ等しくなり、多くの有用な結果が得られます。

$D m$ と $A$ は非常に小さいので、

${\begin{aligned}n&\approx {\dfrac {\frac {A+D_{m}}{2}}{\frac {A}{2}}}\\n&={\frac {A+D_{m}}{A}}\\D_{m}&=An-A\end{aligned}}$

$\therefore D_{m}=A(n-1)$ ^[1]^[4]

一般的な薄いプリズムに対してスネルの法則とプリズムの公式を用いた同様のアプローチを使用すると、偏差角度に関してまったく同じ結果が得られます。

$i$ 、 $e$ 、 $r$ は小さいので、

$n\approx {\frac {i}{r_{1}}},n\approx {\frac {e}{r_{2}}}$

プリズムの公式から、 ${\begin{aligned}\delta &=nr_{1}+nr_{2}-A\\&=n(r_{1}+r_{2})-A\\&=nA-A\\&=A(n-1)\end{aligned}}$

したがって、薄いプリズムは常に最小の偏差にあると言えます。

実験的決定

最小偏差は手動で、または分光計を用いて測定できます。プリズムを固定して入射角を調整するか、光源を固定したままプリズムを回転させることで測定できます。^[6]^[7]^[8]

最小分散角

白色光の最小分散角は、プリズムを通過する光線の赤色光線と紫色光線間の最小偏角の差である。^[2]

薄いプリズムの場合、紫色の光の偏角は、赤色光の偏角はです。赤色光と紫色の光の偏角の差は、プリズムによって生じる角度分散と呼ばれます。 $\delta _{v}$ $(n_{v}-1)A$ $\delta _{r}$ $(n_{r}-1)A$ $(\delta _{v}-\delta _{r})=(n_{v}-n_{r})A$

アプリケーション

干渉点に半径を描くと屈折角が等しいことがわかり、偏差が最小であることが証明されます。

虹が発生する要因の一つは、虹の角度（42°）に近い最小偏角で光線が集まることである。^[3]^[9]

また、空気中の六角形の氷結晶のミニプリズムで太陽光が最小22°の偏差で曲がることによって生じるハローやサンドッグなどの現象もこの現象によって生じます。 ^[3]^[10]

参照

参考文献

^ abcd 「第9章光線光学と光学機器」。クラス9向け物理学パートII教科書（PDF）。NCERT。331ページ。
^ abc 「光学-プリズム」。Aレベル物理学チューター。
^ abcde Mark A. Peterson. 「プリズムによる最小偏差」. mtholyoke .マウント・ホリヨーク大学. 2019年5月23日時点のオリジナルよりアーカイブ。
^ ab 「プリズムによる屈折」SchoolPhysics .
^ ab "プリズム". HyperPhysics .
^ 「最小偏差角度」Scribd。
^ 「プリズム分光計を用いた最小偏角測定のための実験装置」ResearchGate。
^ 「プリズム分光計の理論 - 実験 | UKEssays.com」www.ukessays.com . 2025年3月11日閲覧。
^ 「レインボー」. www.schoolphysics.co.uk .
^ 「Halo 22°」HyperPhysics .

外部リンク

カーンアカデミーの最小偏差値パート1とパート2
NCERT教科書のプリズム屈折
Prismによる最小偏差 2019年5月23日アーカイブ、Wayback Machine、Mark A Peterson、Mount Holyoke College

[:1-1] 「第9章光線光学と光学機器」。クラス9向け物理学パートII教科書（PDF）。NCERT。331ページ。

[:2-2] 「光学-プリズム」。Aレベル物理学チューター。

[:0-3] Mark A. Peterson. 「プリズムによる最小偏差」. mtholyoke .マウント・ホリヨーク大学. 2019年5月23日時点のオリジナルよりアーカイブ。

[:3-4] 「プリズムによる屈折」SchoolPhysics .

[:4-5] "プリズム". HyperPhysics .

[6] 「最小偏差角度」Scribd。

[7] 「プリズム分光計を用いた最小偏角測定のための実験装置」ResearchGate。

[8] 「プリズム分光計の理論 - 実験 | UKEssays.com」www.ukessays.com . 2025年3月11日閲覧。

[9] 「レインボー」. www.schoolphysics.co.uk .

[10] 「Halo 22°」HyperPhysics .