エニアグラム(幾何学)
| スターポリゴン |
|---|
幾何学において、エニアグラム(🟙 U+1F7D9)は9つの頂点を持つ平面図形です。ノナグラム、ノンアングル、エニアゴンと呼ばれることもあります。[ 1 ]
「エニアグラム」という言葉は、数字の接頭辞ennea-とギリシャ語の接尾辞-gramを組み合わせたものです。接尾辞gramは、線を意味するγραμμῆ(grammē )に由来します。 [ 2 ]
通常のエニアグラム
正エニアグラムは、9角形の星型多角形です。正エニアゴンと同じ点で構成されていますが、点は一定の間隔で結ばれています。正エニアグラムには2つの形式があります。
- 1 つの形式は 2 点おきに接続され、Schläfli 記号{9/2} で表されます。
- もう 1 つの形式は 4 点ごとに接続され、Schläfli 記号 {9/4} で表されます。
また、{9/3}または3{3}の星型図形もあり、これは通常の九角形の頂点から作られるが、3つの正三角形の複合体として接続される。[ 3 ] [ 4 ](三角形が交互に絡み合っている場合、これはブルニアンリンクになります。)この星型図形は、{6/2}または2{3}、つまりダビデの星にちなんで、ゴリアテの星と呼ばれることもあります。[ 5 ]
| 化合物 | レギュラースター | 通常の複合 | レギュラースター |
|---|---|---|---|
 完全グラフK 9 完全グラフK 9 |  {9/2} {9/2} | 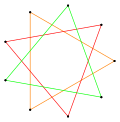 {9/3} または 3{3} {9/3} または 3{3} |  {9/4} {9/4} |
その他のエニアグラムの人物
 二十面体の最終的な星型は、2つの等角面を持つエニアグラム面を持つ。これは9/4の巻き星型多面体であるが、頂点の間隔は等間隔ではない。 二十面体の最終的な星型は、2つの等角面を持つエニアグラム面を持つ。これは9/4の巻き星型多面体であるが、頂点の間隔は等間隔ではない。 |  第四の道の教えと人格のエニアグラムでは、 142857に基づいた正三角形と不規則な六十四卦で構成される不規則なエニアグラムを使用します。 第四の道の教えと人格のエニアグラムでは、 142857に基づいた正三角形と不規則な六十四卦で構成される不規則なエニアグラムを使用します。 |  バハイの九芒星 バハイの九芒星 |  9/3エニアグラム 9/3エニアグラム |
九芒星やエニアグラムは、聖霊の9つの賜物や果実を象徴することもあります。[ 6 ]
大衆文化において
- ヘヴィメタルバンド、スリップノットは以前、{9/3}星型エニアグラム[ 7 ]を使用していましたが、現在は{9/4}多角形をシンボルとして使用しています。以前の図は、彼らのアルバム『All Hope Is Gone』 のジャケットで見ることができます。
参照
参考文献
- ^ 「四角い岩と硬い五角形の間:分数多角形」 2017年9月28日。
- ^ γραμμή、Henry George Liddell、Robert Scott、 A Greek-English Lexicon、ペルセウスについて。
- ^ Grünbaum, B.および GC Shephard; Tilings and Patterns、ニューヨーク:WH Freeman & Co.、(1987)、 ISBN 0-7167-1193-1。
- ^ Grünbaum, B. ; Polyhedra with Hollow Faces、 NATO-ASI Conference on Polytopes ... etc. (Toronto 1993) の議事録、T. Bisztriczky 他編、Kluwer Academic (1994) pp. 43-70。
- ^ Weisstein, Eric W. 「ノナグラム」 . mathworld.wolfram.com .
- ^フリードリヒ・レスト著『キリスト教のシンボル』(1954年)、 ISBN 0-8298-0099-9、13ページ。
- ^ 「スリップノット」。eBay 。
参考文献
- ジョン・H・コンウェイ、ハイディ・バーギエル、チャイム・グッドマン=ストラウス、『The Symmetries of Things』 2008年、ISBN 978-1-56881-220-5(第26章 404ページ:正則星型多面体 次元2)
外部リンク
 ウィキメディア・コモンズのエニアグラム関連メディア
ウィキメディア・コモンズのエニアグラム関連メディア- ノナグラム -- Wolfram MathWorld より

