業務変革

オペレーショナル・トランスフォーメーション（OT ）は、高度なコラボレーション・ソフトウェア・システムにおける幅広いコラボレーション機能をサポートする技術です。OTはもともと、プレーンテキスト文書の共同編集における一貫性維持と同時実行制御のために発明されました。その機能は拡張され、その用途は、グループの元に戻す、ロック、競合解決、操作の通知と圧縮、グループ認識、HTML/XMLおよびツリー構造の文書編集、共同オフィス生産性ツール、アプリケーション共有、共同コンピュータ支援メディア設計ツールなどに拡大しました。[ 1 ] 2009年には、OTは当時のGoogle WaveとGoogle Docsのコラボレーション機能を支える中核技術として採用されました。

歴史

オペレーショナル・トランスフォーメーションは、 1989年にC. EllisとS. Gibbs [ 2 ]によってGROVE（GRoup Outline Viewing Edit）システムで初めて採用されました。数年後、正確性に関する問題がいくつか特定され、これらの問題を解決するためのいくつかのアプローチ[ 3 ] [ 4 ] [ 5 ] [ 6 ]が独立して提案されました。その後10年間、熱心な研究者のコミュニティによってOTの拡張と改善の継続的な取り組みが続きました。1998年には、CEとOTの研究者間のコミュニケーションとコラボレーションを促進するために、共同編集に関する特別利益団体[ 7 ]が設立されました。それ以来、SIGCEはACM、CSCW、GROUP、ECSCWなどの主要なCSCW（コンピュータ支援協働作業）会議と連携して、毎年CEワークショップを開催しています。

システムアーキテクチャ

オペレーション変換を利用するコラボレーション システムでは通常、複製されたドキュメント ストレージが使用されます。このストレージでは、各クライアントが独自のドキュメントのコピーを持ちます。クライアントは、ロックフリーでブロッキングのない方法でローカル コピーを操作し、変更は残りのクライアントに伝播されます。これにより、インターネットなどの高遅延環境でもクライアントの高い応答性が確保されます。クライアントは、別のクライアントから伝播された変更を受信すると、通常は変更を実行する前に変換します。この変換により、アプリケーションに依存する一貫性基準 (不変条件) がすべてのサイトで維持されます。この操作モードにより、 Webなどの高遅延環境での同時ドキュメント編集などのコラボレーション機能を実装するのに特に適したシステムになります。

基本

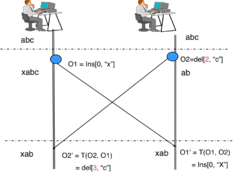
OTの基本的な考え方
OTの基本的な考え方

OTの基本的な考え方は、次のような単純なテキスト編集シナリオを用いて説明できます。文字列「abc」を含むテキスト文書が2つの共同サイトに複製され、2つの同時操作が実行されているとします。

  1. O 1 = Insert[0, "x"] (位置 "0" に文字 "x" を挿入する)
  2. O 2 = Delete[2, "c"] (位置 "2" の文字 "c" を削除する)

共同サイト1と2の2人のユーザーによってそれぞれ生成された文書です。2つの操作がO 1とO 2の順序で（サイト1で）実行されたとします。O 1 の実行後、文書は「xabc」になります。O 1 の後にO 2を実行するには、O 2 をO 1に対して変換する必要があります。O 2 ' = Delete[3, "c"]となります。O 1によって文字「x」が1つ挿入されるため、位置パラメータは1つ増加します。「 xabc」に対してO 2 'を実行すると、正しい文字「c」が削除され、文書は「xab」になります。しかし、O 2 を変換せずに実行すると、文字「c」ではなく「b」が​​誤って削除されます。OTの基本的な考え方は、以前に実行された同時操作の影響に応じて編集操作のパラメータを変換（または調整）し、変換された操作が正しい効果を達成し、文書の一貫性を維持することです。

一貫性モデル

OTの機能の一つは、共同編集システムにおける一貫性維持をサポートすることです。研究コミュニティでは、共同編集システム全般を対象としたものもあれば、OTアルゴリズムに特化したものなど、様々な一貫性モデルが提案されています。

CCモデル

エリスとギブスの1989年の論文「グループウェアシステムにおける並行制御」[ 2 ]では、共同編集システムには2つの一貫性特性が必要であるとされています。

  • 因果関係の保持：コラボレーションプロセスにおいて、因果的に依存する操作の実行順序が、自然な因果関係と同じであることを保証します。2つの操作間の因果関係は、ランポートの「先行発生」関係によって正式に定義されます。2つの操作が因果的に依存していない場合、それらは同時実行されています。2つの同時実行操作は、異なるドキュメントコピーに対して異なる順序で実行できます。
  • 収束: 共有ドキュメントの複製されたコピーが静止時にすべてのサイトで同一であることを確認します (つまり、生成されたすべての操作がすべてのサイトで実行されている)。

同時操作は異なる順序で実行される可能性があり、編集操作は一般に可換ではないため、異なるサイトにある文書のコピーは発散（不整合）する可能性があります。最初のOTアルゴリズムは、EllisとGibbsの論文[ 2 ]で、グループテキストエディタにおける収束を実現するために提案されました。状態ベクトル（または古典的な分散コンピューティングにおけるベクトルクロック）は、優先順位特性を維持するために使用されました。

CCIモデル

CCIモデルは、共同編集システムにおける一貫性管理として提案されました。[ 4 ] [ 8 ] CCIモデルでは、3つの一貫性特性がグループ化されています。

  • 因果律の保存: CC モデルの場合と同じです。
  • 収束: CC モデルの場合と同じです。
  • 意図の保存: 任意の文書状態に対する操作の実行結果が、その操作の意図と同じであることを保証します。操作Oの意図とは、Oが生成された文書状態にOを適用することで達成できる実行結果として定義されます。

CCIモデルは、CCモデルを拡張し、新たな基準として意図の保存を規定しています。収束と意図の保存の本質的な違いは、前者はシリアル化プロトコルによって常に実現できるのに対し、後者は操作が常に元の形式で実行される場合、いかなるシリアル化プロトコルでも実現できない可能性があるという点です。シリアル化不可能な意図の保存特性を実現することは、これまで大きな技術的課題でした。OTは、共同編集システムにおける収束と意図の保存の実現に特に適していることが分かっています。

CCI モデルは、ドキュメントの種類やデータ モデル、操作の種類、またはサポート技術 (OT、マルチバージョン管理、シリアル化、元に戻す/やり直し) に依存しません。特定のデータおよび操作モデルや特定のアプリケーション向けに設計された技術 (OT など) の正確性検証を目的としたものではありません。[ 4 ]では、意図の保持の概念が 3 つのレベルで定義および改良されました。第 1 に、共同編集システムの一般的な一貫性要件として定義されました。第 2 に、一般的な OT 機能の操作コンテキスト ベースの変換前および変換後の条件として定義されました。第 3 に、共同プレーン テキスト エディターでの文字列の挿入と削除という 2 つの基本操作に対する OT 機能の設計をガイドする特定の操作検証基準として定義されました。

CSMモデル

CCIモデルでは、形式的証明のために意図保存の条件が正式に規定されていませんでした。SDT [ 9 ]アプローチとLBT [ 10 ]アプローチは、証明可能な代替条件を形式化しようと試みています。これら2つのアプローチで提案されている整合性モデルは、以下の形式的条件から構成されています。

  • 因果関係：CCモデルと同じ定義
  • 単一操作効果: 任意の実行状態で任意の操作を実行すると、その生成状態と同じ効果が得られます。
  • 複数操作の効果: 任意の2つの操作の効果関係は、両方の操作がどの状態で実行された後も維持されます。

CAモデル

上記のCSMモデルでは、システム内のすべてのオブジェクトの全順序を指定する必要があります。実質的には、この指定は挿入操作によって導入される新しいオブジェクトに限定されます。しかし、全順序の指定には、挿入の同点（つまり、現在の2つの操作によって同じ位置に挿入される新しいオブジェクト）を破棄するといった、アプリケーション固有のポリシーが必要になります。その結果、全順序はアプリケーション固有のものになります。さらに、このアルゴリズムでは、変換関数と制御手順において全順序を維持する必要があり、これがアルゴリズムの時間/空間計算量を増加させます。

一方、CAモデルは許容理論に基づいています。[ 11 ] CAモデルには2つの側面があります。

  • 因果関係：CCモデルと同じ定義
  • 許容性: すべての操作の呼び出しは実行状態で許容されます。つまり、すべての呼び出しは、以前の呼び出しによって確立された効果関係 (オブジェクトの順序) に違反してはなりません。

これら2つの条件は収束を意味する。すべての協力サイトは、同じ順序にある​​同じオブジェクト集合が存在する状態に収束する。さらに、順序は操作生成時の効果によって実質的に決定される。これら2つの条件はオブジェクトの順序にも追加の制約を課すため、実際には収束よりも強い。CAモデルと設計/証明アプローチは、2005年の論文[ 11 ]で詳細に説明されている。これにより、オブジェクトの全順序を一貫性モデルで指定し、アルゴリズム内で維持する必要がなくなり、アルゴリズムの時間/空間計算量が削減される。

OTシステム構造

OTは複数のコンポーネントから構成されるシステムです。OTシステムを設計するための確立された戦略の一つ[ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 12 ] [ 13 ]は、高レベルの変換制御（または統合）アルゴリズムを低レベルの変換機能から分離することです。

OT 制御アルゴリズム(同時実行性/コンテキスト関係に応じて、どの操作が他の操作に対して変換されるかを決定する)
OT のプロパティと条件(アルゴリズムと関数の間で責任を分割する)
OT 変換関数(操作の種類、位置、その他のパラメータに応じて、基本操作のペアをどのように変換するかを決定します)

変換制御アルゴリズムは、次の事項を決定することに関係しています。

  1. 因果的に準備された新しい操作に対してどの操作を変換する必要があるか
  2. 変換の順序

制御アルゴリズムは、対応する変換関数のセットを呼び出します。これらの関数は、操作の種類、位置、その他のパラメータに応じて、ある操作を別の操作に変換する方法を決定します。これら2つの層の正確性に関する責任は、一連の変換プロパティと条件によって正式に規定されます。制御アルゴリズム、機能、通信トポロジが異なるOTシステムでは、それぞれ異なる変換プロパティのセットを維持する必要があります。OTシステムをこれらの2つの層に分離することで、異なるデータおよび操作モデルを持つさまざまな種類のアプリケーションに適用可能な汎用的な制御アルゴリズムを設計できます。

もう一つの代替アプローチは[ 11 ]で提案されました。彼らのアプローチでは、OTアルゴリズムは2つの形式化された正しさの基準を満たしていれば正しいとされます。

  1. 因果関係の保存
  2. 許容性の維持

これら2つの基準が満たされている限り、すべての操作がすべてのサイトで実行された後、データレプリカは（追加の制約条件付きで）収束します。収束を達成するために、実行順序を強制する必要はありません。彼らのアプローチは、一般的に、まずいくつかの変換関数の十分条件を特定して証明し、次にそれらの十分条件を保証する制御手順を設計することです。このようにして、制御手順と変換関数は相乗的に機能し、正確性、すなわち因果関係と許容性の維持を実現します。彼らのアプローチでは、TP2などの変換特性を満たす必要はありません。なぜなら、（包括的な）変換関数がすべての可能なケースで機能する必要がないからです。

OTデータと運用モデル

各OTシステムには、2つの基礎モデルが存在します。1つは文書内のデータオブジェクトが操作によってアドレス指定される方法を定義するデータモデル、もう1つはOT関数によって直接変換できる一連の操作を定義する操作モデルです。異なるOTシステムは、異なるデータモデルと操作モデルを持つ場合があります。たとえば、最初のOTシステム[ 2 ]のデータモデルは単一の線形アドレス空間であり、その操作モデルは文字単位の挿入と削除という2つの基本操作で構成されています。基本操作モデルは、Word文書の共同処理[ 14 ]と3Dモデル編集[ 15 ]をサポートするために、3つ目の基本操作である更新を含むように拡張されています。基本的なOTデータモデルは、複数の線形アドレス指定ドメインの階層に拡張されており[ 16 ] [ 17 ] [ 18 ]、幅広い文書をモデル化できます。アプリケーション固有のデータモデルをOT準拠のデータモデルにマッピングするには、データ適応プロセスが必要になることがよくあります。[ 19 ] [ 20 ]

OT システムでアプリケーション レベルの操作をサポートするには、次の 2 つのアプローチがあります。

  1. 汎用操作モデルアプローチ：挿入、削除、更新という3つの基本操作に対する変換関数を考案する。[ 19 ]このアプローチでは、アプリケーション操作をこれらの基本操作にマッピングするための操作適応プロセスが必要となる。このアプローチでは、OT操作モデルが汎用的であるため、変換関数を異なるアプリケーションで再利用することができる。
  2. アプリケーション固有の操作モデルアプローチ：アプリケーション操作の各ペアに対して変換関数を考案する。[ 20 ] [ 21 ] m個の異なる操作を持つアプリケーションの場合、このアプリケーションをサポートするにはm×m個の変換関数が必要となる。このアプローチでは、変換関数はアプリケーション固有であり、異なるアプリケーションで再利用することはできない。

OT機能

様々なOT機能が、異なる機能を持つOTシステム向けに設計され、様々な用途で使用されています。異なるOTシステムで使用されるOT機能は、名称が異なる場合がありますが、以下の2つのカテゴリに分類できます。

  • 包含変換（または順方向変換）：または。これは、 の操作を別の操作に対して変換し、 の影響が効果的に含まれるようにします。これは、例えば、異なるノードへの 2 つの挿入の場合に当てはまります。私T（お1つの、おb）{\displaystyle IT(O_{a},O_{b})}T（op1、op2）{\displaystyle T(op_{1},op_{2})}お1つの{\displaystyle O_{a}}おb{\displaystyle O_{b}}おb{\displaystyle O_{b}}
  • 排除変換（または後方変換）：これは、操作を別の操作に対して変換し、その影響を効果的に排除する。これは、例えば、異なるノードにおける挿入と削除の場合である[ 22 ]。ET（お1つの、おb）{\displaystyle ET(O_{a},O_{b})}T−1（op1、op2）{\displaystyle T^{-1}(op_{1},op_{2})}お1つの{\displaystyle O_{a}}おb{\displaystyle O_{b}}おb{\displaystyle O_{b}}

例えば、文字列型にins( p,c,sid )という操作があるとします。ここでpは挿入位置、cは挿入する文字、sidは操作を生成したサイトの識別子です。このとき、次のような包含変換関数を書くことができます。[ 23 ]

func T (ins( p 1 , c 1 , sid 1 ), ins( p 2 , c 2 , sid 2 )): if ( p 1 < p 2 ) return ins( p 1 , c 1 , sid 1 ) else if ( p 1 = p 2 and sid 1 < sid 2 ) return ins( p 1 , c 1 , sid 1 ) else return ins( p 1 +1, c 1 , sid 1 )

次のような除外変換関数を書くこともできる: [ 23 ]

func T −1 (ins( p 1 , c 1 , sid 1 ), ins( p 2 , sid 2 )): if ( p 1 < p 2 ) return ins( p 1 , c 1 , sid 1 ) else if ( p 1 = p 2 and sid 1 < sid 2 ) return ins( p 1 , c 1 , sid 1 ) else return ins( p 1 −1, c 1 , sid 1 )

OTシステムの中には、IT機能とET機能の両方を使用するものもあれば、IT機能のみを使用するものもあります。OT機能設計の複雑さは、様々な要因によって決まります。

  • OTシステムの機能性：OTシステムがdo（一貫性維持）、undo、ロック、[ 24 ]認識、アプリケーション共有、[ 19 ] [ 25 ] [ 26 ] [ 27 ]などをサポートしているかどうか。
  • OT システムにおける正確性の責任: 満たすべき変換特性 (CP1/TP1、CP2/TP2、IP2、IP3、RP)、ET が使用されるかどうか。
  • OTシステムの操作モデル：OT操作モデルが汎用的なもの（例えば、基本的な挿入、削除、更新）か、アプリケーション固有のもの（対象アプリケーションのすべての操作）か。
  • OT システムのデータ モデル: 各操作のデータが文字単位 (個々のオブジェクト)、文字列単位 (オブジェクトのシーケンス)、階層的、またはその他の構造であるか。

変換プロパティ

OTシステムの正確性を保証するための様々な変換特性が特定されている。これらの特性は、変換制御アルゴリズム[ 4 ] [ 5 ] [ 13 ] [ 20 ] [ 28 ] [ 29 ]または変換関数[ 30 ]によって維持することができる。OTシステムの設計によって、これらのコンポーネント間の役割分担は異なる。これらの特性の仕様と、それらを必要とする前提条件を以下に示す。

収束特性

TP1プロパティの図解
TP2物件の図解

次の 2 つの特性は、収束の達成に関連しています。

  • CP1/TP1 :同じ状態で定義されている同時操作とのすべてのペアについて、変換関数 T が CP1/TP1 プロパティを満たすのは、次の場合のみです。ここで、 は、に続く操作のシーケンスを表します。また、 は、2 つの操作シーケンスが同等であることを示します。CP1 /TP1 前提条件: CP1/TP1 は、OT システムで任意の 2 つの操作を異なる順序で実行できる場合にのみ必要です。op1{\displaystyle op_{1}}op2{\displaystyle op_{2}}op1∘T（op2、op1）≡op2∘T（op1、op2）{\displaystyle op_{1}\circ T(op_{2},op_{1})\equiv op_{2}\circ T(op_{1},op_{2})}op私∘opj{\displaystyle op_{i}\circ op_{j}}op私{\displaystyle op_{i}}opj{\displaystyle op_{j}}≡{\displaystyle \equiv}
  • CP2/TP2 :同じドキュメント状態で定義されている3 つの同時操作およびごとに、変換関数 T が CP2/TP2 プロパティを満たすのは、次の場合のみです。 CP2/TP2 は、2 つの同等な操作シーケンスに関して変換された 2 つの操作間の等価性を規定します。が後に続く操作シーケンスに対するの変換は、およびによって形成されるシーケンスに対するの変換と同じ操作を与える必要があります。CP2/TP2 前提条件: CP2/TP2 は、OT システムで 2 つの操作が許可され、2 つの異なるドキュメント状態 (またはコンテキスト) で IT 変換される場合にのみ必要です。op1、op2{\displaystyle op_{1},op_{2}}op3{\displaystyle op_{3}}T（op3、op1∘T（op2、op1））＝T（op3、op2∘T（op1、op2））{\displaystyle T(op_{3},op_{1}\circ T(op_{2},op_{1}))=T(op_{3},op_{2}\circ T(op_{1},op_{2}))}op3{\displaystyle op_{3}}op2{\displaystyle op_{2}}T（op1、op2）{\displaystyle T(op_{1},op_{2})}op3{\displaystyle op_{3}}op1{\displaystyle op_{1}}T（op2、op1）{\displaystyle T(op_{2},op_{1})}op1{\displaystyle op_{1}}op2{\displaystyle op_{2}}

逆の性質

望ましいグループ元に戻す効果を実現するには、次の3つのプロパティが関係します。

  • IP1 : 任意の文書状態Sとシーケンス が与えられた場合、 が成り立ちます。これは、シーケンス が文書状態への影響に関して単一の恒等演算 I と等価であることを意味します。この特性は、OTシステムにおいて正しい元に戻す効果を実現するために必要ですが、IT機能とは関係ありません。op∘op¯{\displaystyle op\circ {\overline {op}}}S∘op∘op¯＝S{\displaystyle S\circ op\circ {\overline {op}}=S}op∘op¯{\displaystyle op\circ {\overline {op}}}
  • IP2 : IP2 という性質は、シーケンスが他の操作の変換に影響を与えないことを表します。変換関数が IP2 を満たすのは、次の場合のみです。つまり、シーケンスに対する変換の結果は、恒等演算 I に対する変換の結果と等しくなります。IP2の前提条件: IP2 は、OT システムが、操作を 1対の do 操作と undo 操作のペアに対して1 つずつ変換することを許可している場合にのみ必要です。op∘op¯{\displaystyle op\circ {\overline {op}}}T（op×、op∘op¯）＝op×{\displaystyle T(op_{x},op\circ {\overline {op}})=op_{x}}op×{\displaystyle op_{x}}op∘op¯{\displaystyle op\circ {\overline {op}}}op×{\displaystyle op_{x}}op×{\displaystyle op_{x}}op∘op¯{\displaystyle op\circ {\overline {op}}}
  • IP3 :同じ文書状態（またはコンテキスト）で定義された2つの同時操作とが与えられている場合、およびの場合。変換関数がIP3プロパティを満たすのは、 の場合のみであり、これは、変換された逆操作が変換された操作 の逆操作に等しいことを意味します。IP3前提条件: IP3は、OTシステムが、と同じ文書状態（またはコンテキスト的に同等）で定義された同時操作に対して逆操作を変換することを許可する場合にのみ必要です。op1{\displaystyle op_{1}}op2{\displaystyle op_{2}}op1¯′＝T（op1¯、T（op2、op1））{\displaystyle {\overline {op_{1}}}'=T({\overline {op_{1}}},T(op_{2},op_{1}))}op1′¯＝T（op1、op2）¯{\displaystyle {\overline {op_{1}'}}={\overline {T(op_{1},op_{2})}}}op1¯′＝op1′¯{\displaystyle {\overline {op_{1}}}'={\overline {op_{1}'}}}op1¯′{\displaystyle {\overline {op_{1}}}'}op1′¯{\displaystyle {\overline {op_{1}'}}}op1¯{\displaystyle {\overline {op_{1}}}}op2{\displaystyle op_{2}}op1{\displaystyle op_{1}}

OT制御（統合）アルゴリズム

様々なOT制御アルゴリズムが、異なる機能を持つOTシステムや異なるアプリケーション向けに設計されてきました。OT制御アルゴリズム設計の複雑さは、複数の要因によって決まります。重要な差別化要因は、アルゴリズムが同時実行制御（do）やグループundoをサポートできるかどうかです。[ 3 ] [ 8 ] [ 12 ] [ 29 ] [ 31 ]さらに、異なるOT制御アルゴリズム設計は、以下の点で異なるトレードオフをもたらします。

  • 制御アルゴリズムと変換機能の間で正確性の責任を割り当てること、および
  • OT システムの時空間複雑度。

並行制御のための既存のOT制御アルゴリズムのほとんどは、因果関係／並行性の理論を理論的根拠として採用している。因果的に関連する操作は因果順序で実行されなければならない。並行操作は実行前に変換されなければならない。しかし、並行性の条件だけではすべてのOT変換条件を捉えることはできないことはよく知られていた。[ 3 ] [ 4 ] [ 5 ] [ 8 ] [ 32 ]最近の研究では、操作コンテキスト理論がドキュメント状態の概念を明示的に表現するために提案されており、これはOT制御アルゴリズムの設計と検証を支援するためのOT変換条件を形式的に表現するために使用できる。[ 29 ]

次の表は、既存のOT制御/統合アルゴリズムの概要を示しています。

OT制御/統合アルゴリズム（システム） 必要な変換関数の種類 OTベースのDoをサポートしますか? OT ベースの Undo をサポートしますか? 制御アルゴリズムでサポートされる変換プロパティ 変換関数でサポートされる変換プロパティ 変換順序と伝播制約 タイムスタンプ
dOPT [ 2 ] (グローブ) T（イタリア語） はい いいえ なし CP1/TP1、CP2/TP2 因果関係の順序 状態ベクトル
選択的元に戻す[ 12 ] (DistEdit) 転置（IT と ET） いいえ 選択的な元に戻す 該当なし CP1/TP1、CP2/TP2、RP、IP1、IP2、IP3 因果関係の順序 ?
adOPTed [ 3 ] [ 31 ] (JOINT EMACS) Lトランスフォーメーション（IT） はい 時系列で元に戻す IP2、IP3 CP1/TP1、CP2/TP2、IP1 因果関係の順序 状態ベクトル
木星[ 5 ]xform（IT） はい いいえ CP2/TP2 CP1/TP1 因果秩序 + 中央変換サーバー スカラー
Google Wave OT [ 20 ]変換と合成（IT） はい いいえ CP2/TP2 CP1/TP1 因果順序 + 中央変換サーバー + 停止・待機伝播プロトコル スカラー
獲得[ 4 ] (削減) ITとET はい いいえ CP1/TP1、CP2/TP2 なし 因果順序 + 不連続全順序 状態ベクトル
GOTO [ 6 ] (REDUCE、CoWord、CoPPT、CoMaya) ITとET はい いいえ なし CP1/TP1、CP2/TP2 因果関係の順序 状態ベクトル
AnyUndo [ 8 ] (REDUCE、CoWord、CoPPT、CoMaya) ITとET いいえ あらゆる操作を元に戻す IP2、IP3、RP IP1、CP1/TP1、CP2/TP2 因果関係の順序 状態ベクトル
SCOP [ 28 ] (ニース) それ はい いいえ CP2/TP2 CP1/TP1 因果秩序 + 中央変換サーバー スカラー
COT [ 29 ] (REDUCE、CoWord、CoPPT、CoMaya) それ はい あらゆる操作を元に戻す CP2/TP2、IP2、IP3 CP1/TP1（ETがないのでIP1は不要） 因果順序 + 不連続全順序 コンテキストベクトル
ティボット[ 33 ]それ はい いいえ CP2/TP2 CP1/TP1 因果関係の順序 スカラー
SOCT4 [ 13 ]フォワードトランスフォーメーション（IT） はい いいえ CP2/TP2 CP1/TP1 因果順序 + 連続全順序 スカラー
SOCT2 [ 32 ]フォワード・トランスフォーメーション（IT）とバックワード・トランスフォーメーション（ET） はい いいえ なし CP1/TP1、CP2/TP2、RP 因果関係の順序 状態ベクトル
MOT2 [ 34 ]フォワードトランスフォーメーション（IT） はい いいえ ? CP1/TP1、CP2/TP2 ? スカラー

連続全順序は、欠落した要素を検出できる 厳密な全順序です。つまり、1、2、3、4、... は連続全順序ですが、1、2、3、5、... は連続全順序ではありません。

[ 10 ] [ 11 ]で提案されている変換ベースのアルゴリズムは、前述の代替整合性モデル「CSM」および「CA」に基づいています。これらのアルゴリズムのアプローチは、表に記載されているものとは異なります。因果関係の保存にはベクトルタイムスタンプを使用します。その他の正当性条件は、「単一」/「複数」操作効果の関係の保存、または「許容性」の保存です。これらの条件は、制御手順と変換関数の相乗効果によって保証されます。これらの研究ではTP1/TP2について議論する必要はありません。したがって、上記の表には記載されていません。

他にも、変換アルゴリズムの設計に代替的な方法を模索する楽観的一貫性制御アルゴリズムはいくつか存在するが、上記の分類や特徴づけにはうまく適合しない。例えば、Mark and Retrace [ 35 ]

OTの正確性の問題により、WOOT [ 36 ] 、 Logoot [ 37 ]、Causal Trees(CT) [ 38 ]などの変換を必要としないポストOT方式が導入されました。「ポストOT」方式は文書をアトミック操作に分解しますが、一意のシンボル識別子、ベクトルタイムスタンプ、および/またはトゥームストーンの組み合わせを使用することで、操作を変換する必要性を回避します。

OT批判

テキスト内のオフセットによって操作を定義するという古典的なOTアプローチは、一見単純で自然なように思えますが、現実世界の分散システムでは深刻な問題が生じます。つまり、操作は有限の速度で伝播し、参加者の状態はしばしば異なるため、結果として生じる状態と操作の組み合わせを予測し理解することは非常に困難です。LiとLiは、「複雑なケースカバレッジを考慮する必要があるため、2つの文字単位のプリミティブ（挿入と削除）のみを扱うOTアルゴリズムであっても、形式的な証明は非常に複雑でエラーが発生しやすい」と述べています。[ 39 ]

同様に、元Google WaveエンジニアでShare.JSライブラリの作者でもあるジョセフ・ジェントルは、「残念ながら、OTの実装は大変です。さまざまなトレードオフを持つアルゴリズムが数百万個あり、そのほとんどは学術論文の中に埋もれています。[…] Waveの開発には2年かかりましたが、もし今日書き直したとしても、もう一度書くのにほぼ同じくらいの時間がかかるでしょう。」と書いています。 [ 40 ]しかし、後に彼は「今ではWaveの実装に2年かかるとは思っていません。これは主にウェブフレームワークとウェブブラウザの進歩によるものです。」とコメントを修正しています。[ 41 ]

OTが機能するには、データへのあらゆる変更をキャプチャする必要があります。「状態のスナップショットを取得することは通常簡単ですが、編集をキャプチャすることは全く別の問題です。[…] 現代のユーザーインターフェースの豊富さは、特にブラウザベースの環境では、これが問題になることがあります。」OTの代替手段は差分同期です。[ 42 ]

OT の別の代替手段は、競合のない複製されたデータ型のシーケンス型を使用することです。

参照

参考文献

  1. ^ Sun, Chengzheng. 「OT FAQ」 。2020年6月23日時点のオリジナルよりアーカイブ。
  2. ^ a b c d e f Ellis, CA; Gibbs, SJ (1989). 「グループウェアシステムにおける並行制御」. ACM SIGMOD Record . 18 (2): 399– 407. CiteSeerX 10.1.1.465.2026 . doi : 10.1145/67544.66963 . S2CID 6488575 .  
  3. ^ a b c d e Ressel, Matthias、Nitsche-Ruhland, Doris、Gunzenhäuser, Rul (1996).グループエディタにおける並行処理制御とundo機能への統合的かつ変換指向のアプローチ. CSCW '96: Proceedings of the 1996 ACM conference on Computer supporting cooperative work. pp.  288– 297. doi : 10.1145/240080.240305 .{{cite conference}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  4. ^ a b c d e f g Chengzheng Sun; Xiaohua Jia; Yanchun Zhang; Yun Yang; David Chen (1998). 「リアルタイム協調編集システムにおける収束、因果関係の維持、意図の維持の実現」ACM Trans. Comput.-Hum. Interact . 5 (1): 63– 108. CiteSeerX 10.1.1.56.1251 . doi : 10.1145/274444.274447 . S2CID 14447070 .  
  5. ^ a b c d e Nichols, DA; Curtis, P.; Dixon, M.; Lamping, J. (1995). 「Jupiterコラボレーションシステムにおける高遅延、低帯域幅のウィンドウ処理」 . Proceedings of the 8th Annual ACM Symposium on User Interface and Software Technology : 111– 120. 2015年11月30日時点のオリジナルよりアーカイブ。 2009年9月27日閲覧。
  6. ^ a b Sun, C.; Ellis, C. (1998).リアルタイムグループエディタにおける運用上の変革：問題点、アルゴリズム、そして成果. 1998 ACM コンピュータ支援協調作業会議議事録. ACM Press ニューヨーク、ニューヨーク、米国. pp.  59– 68.
  7. ^ 「SIGCE - 共同編集に関する国際特別利益団体」 . cooffice.ntu.edu.sg . 2012年12月24日時点のオリジナルよりアーカイブ。2020年1月10日閲覧。
  8. ^ a b c d C. Sun (2002). 「グループエディタにおける並行逆操作としてのUndo」ACM Trans. Comput.-Hum. Interact . 9 (4): 309– 361. doi : 10.1145/586081.586085 . S2CID 47453660 . 
  9. ^ Du Li; Rui Li (2004).グループエディターにおける操作効果関係の保持. ACM CSCW'04 コンピュータ支援協働作業会議議事録. ACM Press ニューヨーク、ニューヨーク、米国. pp.  457– 466.
  10. ^ a b Rui Li; Du Li (2007). 「リアルタイムグループエディターのための新しい運用変換フレームワーク」. IEEE Transactions on Parallel and Distributed Systems . 18 (3). IEEE Transactions on Parallel and Distributed Systems: 307– 319. doi : 10.1109/TPDS.2007.35 . S2CID 18822760 . 
  11. ^ a b c d Rui Li; Du Li (2005).グループウェアにおける可換性に基づく同時実行制御. 第1回IEEEコラボレーティブコンピューティング会議：ネットワーク、アプリケーション、ワークシェアリング（CollaborateCom'05）の議事録.
  12. ^ a b c Prakash, Atul & Knister, Michael J. (1994). 「協調システムにおけるアクションを元に戻すためのフレームワーク」. ACM Trans. Comput.-Hum. Interact . 1 (4): 295– 330. CiteSeerX 10.1.1.51.4793 . doi : 10.1145/198425.198427 . S2CID 10705127 .  
  13. ^ a b c Vidot, N.; Cart, M.; Ferrie, J.; Suleiman, M. (2000).分散型リアルタイム協調環境におけるコピー収束(PDF) . Proceedings of the 2000 ACM conference on Computer supported cooperative work. ACM Press New York, NY, USA. pp.  171– 180. 2004年10月12日時点のオリジナル(PDF)からのアーカイブ。
  14. ^ D. Sun、S. Xia、C. Sun、D. Chen (2004).協調的ワードプロセッシングのための操作変換. ACM Conf. on Computer-Supported Cooperative Work 会議論文集. pp.  437– 446.
  15. ^ Agustina、F. Liu、S. Xia、H. Shen、C. Sun (2008年11月). CoMaya: 高度なコラボレーション機能を{3D}デジタルメディアデザインツールに組み込む. Proc. of ACM Conf. on Computer-Supported Cooperative Work. pp.  5– 8.
  16. ^ Davis, Aguido Horatio、Sun, Chengzheng、Lu, Junwei (2002).標準的な汎用マークアップ言語への操作変換の一般化. CSCW '02: Proceedings of the 2002 ACM conference on Computer supported cooperative work. New Orleans, Louisiana, USA. pp.  58– 67. doi : 10.1145/587078.587088 .{{cite conference}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  17. ^ Claudia-Lavinia Ignat; Moira C. Norrie (2003). treeOPTアルゴリズムに基づくカスタマイズ可能な共同エディタ. ECSCW'03: 第8回ヨーロッパコンピュータ支援協同作業会議議事録. Kluwer Academic Publishers. pp.  315– 334. doi : 10.1007/978-94-010-0068-0_17 .
  18. ^ Claudia-Lavinia Ignat; Moira C. Norrie (2008). 「階層的文書の多段階編集」. Computer Supported Cooperative Work . 17 ( 5–6 ): 423– 468. doi : 10.1007/s10606-007-9071-2 . S2CID 42752275 . 
  19. ^ a b c C.Sun, S.Xia, D.Sun, D.Chen, H.Shen, W.Cai (2006). 「マルチユーザーリアルタイムコラボレーションのためのシングルユーザーアプリケーションの透過的適応」ACM Trans. Comput.-Hum. Interact . 13 (4): 531– 582. doi : 10.1145/1188816.1188821 . S2CID 14184705 . {{cite journal}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  20. ^ a b c d「Google Wave Operational Transform」。2009年5月31日時点のオリジナルよりアーカイブ。2009年5月29日閲覧。
  21. ^ Christopher R. Palmer; Gordon V. Cormack (1998).分散共有スプレッドシートのための演算変換. CSCW '98: Proceedings of the 1998 ACM conference on Computer supported cooperative work. ACM Press. pp.  69– 78. doi : 10.1145/289444.289474 .
  22. ^ Kagorskii, Anton. 「自動紛争解決アルゴリズムとしてのオペレーショナル・トランスフォーメーション」 medium.com . 2021年12月21日閲覧。
  23. ^ a b「共同編集システムにおける一貫性を確保するためのトゥームストーン変換関数」 IEEE共同コンピューティング会議：ネットワーキング、アプリケーション、ワークシェアリング。2006年11月7日。
  24. ^ C. Sun & R. Sosic (1999).分散リアルタイムグループエディタにおける操作変換と統合されたオプションロック機能. 第18回ACM分散コンピューティング原理シンポジウム論文集. pp.  43– 52.
  25. ^ Begole, James、Rosson, Mary Beth、Shaffer, Clifford A. (1999). 「柔軟なコラボレーションの透明性：複製されたアプリケーション共有システムにおけるワーカーの独立性のサポート」ACM Trans. Comput.-Hum. Interact . 6 (2): 95– 132. CiteSeerX 10.1.1.23.1185 . doi : 10.1145/319091.319096 . S2CID 17895848 .  {{cite journal}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  26. ^ Li, Du & Li, Rui (2002).異機種シングルユーザーアプリケーションの透過的な共有と相互運用性. CSCW '02: 2002 ACM コンピュータ支援協調作業会議議事録. 米国ニューオーリンズ. pp.  246– 255.
  27. ^ Li, Du & Lu, Jiajun (2006).使い慣れたシングルユーザーエディタの透過的な共有のための軽量アプローチ. CSCW '06: 2006年20周年記念コンピュータ支援協調作業会議議事録. バンフ、アルバータ州、カナダ. pp.  139– 148. doi : 10.1145/1180875.1180896 .
  28. ^ a b Shen, Haifeng & Sun, Chengzheng (2002).協調システムのための柔軟な通知. CSCW '02: Proceedings of the 2002 ACM conference on Computer supporting cooperative work. pp.  77– 86. doi : 10.1145/587078.587090 .
  29. ^ a b c d D. Sun & C. Sun (2009). 「分散協調編集システムのためのコンテキストベースの運用変換」. IEEE Transactions on Parallel and Distributed Systems . 20 (10): 1454– 1470. doi : 10.1109/TPDS.2008.240 . S2CID 18740053 . 
  30. ^ Gerald Oster、Pascal Molli、Pascal Urso、Abdessamad Imine (2006). 「共同編集システムにおける一貫性確保のためのTombstone変換関数」(PDF) . Procs. 2nd Intl. Conf. On Collaborative Computing: Networking, Appln. And Worksharing . 2007年7月26日閲覧.
  31. ^ a b M. Ressel & R. Gunzenhauser (1999).グループ元に戻す問題の軽減. ACMグループ作業支援会議論文集. pp.  131– 139.
  32. ^ a b Suleiman, M.; Cart, M.; Ferrié, J. (1998).分散型モバイル協調環境における並行操作. 第14回国際データエンジニアリング会議論文集, 2008年2月. pp.  23– 27. doi : 10.1109/ICDE.1998.655755 .
  33. ^ R. Li, D. Li & C. Sun (2004).インタラクティブグループウェアアプリケーションのための時間間隔ベースの一貫性制御アルゴリズム. ICPADS '04: Proceedings of the Parallel and Distributed Systems, Tenth International Conference. p. 429. doi : 10.1109/ICPADS.2004.12 .
  34. ^ M. Cart, Jean Ferrié (2007). P2P環境における運用変換に基づく同期化(PDF) . Proceedings of the 3rd International Conference on Collaborative Computing: Networking, Applications and Worksharing. pp.  127– 138. 2007年7月26日閲覧.
  35. ^ Gu, Ning、Yang, Jiangming、Zhang, Qiwei (2005).グループウェアシステムにおけるマーク＆リトレース技術に基づく一貫性維持. GROUP '05: 2005年国際ACM SIGGROUPグループワーク支援会議議事録. pp.  264– 273. doi : 10.1145/1099203.1099250 .{{cite conference}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  36. ^ Imine, Abdessamad、Molli, Pascal、Oster, Gerald、Urso, Pascal (2005).オペレーション変換を必要としないリアルタイムグループエディター. INRIA研究報告書 RR-5580. p. 24.{{cite conference}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  37. ^ Stephane Weiss、Pascal Urso、Pascal Molli (2010). 「Logoot-Undo: P2Pネットワーク上の分散型共同編集システム」. IEEE Transactions on Parallel and Distributed Systems . 21 (8). IEEE Transactions on Parallel and Distributed Systems: 1162. doi : 10.1109/TPDS.2009.173 . S2CID 14172605 . 
  38. ^ Victor Grishchenko (2010).正規表現で実装された埋め込みリビジョン管理機能を備えたディープハイパーテキスト(PDF) .第6回国際Wikiシンポジウム (WikiSym '10) の議事録. 2012年3月9日時点のオリジナル(PDF)からアーカイブ。 2010年6月30日閲覧。
  39. ^ Du Li & Rui Li (2010). 「共同編集システムのための許容性に基づく運用変換フレームワーク」.コンピュータ支援協働作業. 19 (1). コンピュータ支援協働作業: 1– 43. doi : 10.1007/s10606-009-9103-1 . S2CID 35748875 . 
  40. ^ "ShareJS" . 2011年11月6日. 2012年5月11日時点のオリジナルよりアーカイブ。 2013年8月16日閲覧。
  41. ^ 「そう、それは私です！ 念のため言っておきますが、あの波が2年かかるとはもう信じていません… | Hacker News」news.ycombinator.com 2019年2月13日閲覧。
  42. ^ Neil Fraser (2009年1月). 「Differential Synchronization」 .

関連するオンライン講演

「 https://en.wikipedia.org/w/index.php?title=Operational_transformation&oldid=1319509671」より取得