基数木
早口言葉の単語の基数木の例

コンピュータサイエンスにおいて、基数木（基数トライ、コンパクトプレフィックスツリー、圧縮トライとも呼ばれる）は、唯一の子である各ノードがその親とマージされる、空間最適化されたトライ（プレフィックスツリー）を表すデータ構造です。その結果、すべての内部ノードの子の数は、最大で基数木の基数rになります。ここで、 r = 2 x（ある整数x ≥ 1）です。通常の木とは異なり、エッジには単一の要素だけでなく、要素のシーケンスでラベル付けできます。これにより、基数木は、小さなセット（特に文字列が長い場合）や、長いプレフィックスを共有する文字列のセットに対して、はるかに効率的になります。

通常の木 (キー全体が最初から不一致の点までまとめて比較される) とは異なり、各ノードのキーはビットのチャンクごとに比較されます。この場合、そのノードのそのチャンク内のビットの量は、基数トライの基数rです。rが2 のとき、基数トライはバイナリ (つまり、キーのそのノードの 1 ビット部分を比較する) であり、トライの深さを最大化することを犠牲にしてスパース性を最小限に抑えます。つまり、キー内の非発散ビット文字列の融合を最大化します。r ≥ 4 が 2 の累乗である場合、基数トライはr元トライであり、潜在的なスパース性を犠牲にして基数トライの深さを減らします。

最適化として、文字列への2つのポインタ（最初の要素と最後の要素）を使用して、エッジラベルを一定サイズで保存することができます。[ 1 ]

この記事の例では文字列を文字のシーケンスとして示していますが、文字列要素の型は任意に選択できます。たとえば、マルチバイト文字エンコーディングまたはUnicode を使用する場合は、文字列表現のビットまたはバイトとして選択できます。

アプリケーション

基数木は、文字列として表現できるキーを持つ連想配列の構築に役立ちます。特にIPルーティングの分野で応用されています[ 2 ] [ 3 ] [ 4 ]。IPルーティングでは、いくつかの例外を除いて広範囲の値を格納できるため、IPアドレスの階層構造に適しています[ 5 ]。また、情報検索におけるテキスト文書の転置インデックスにも使用されます。

オペレーション

基数木は、挿入、削除、および検索操作をサポートします。挿入は、格納されるデータ量を最小限に抑えながら、トライに新しい文字列を追加します。削除は、トライから文字列を削除します。検索操作には、完全一致検索、先行文字列の検索、後続文字列の検索、およびプレフィックスを持つすべての文字列の検索が含まれます（ただし、これらに限定されるわけではありません）。これらの操作はすべてO( k )で実行されます。ここで、kはセット内のすべての文字列の最大長であり、長さは基数木トライの基数に等しいビット数で測定されます。

見上げる

パトリシアトライ内の文字列の検索

ルックアップ操作は、トライツリー内に文字列が存在するかどうかを判定します。ほとんどの操作は、特定のタスクを処理するために、このアプローチを何らかの形で変更します。例えば、文字列の終端ノードが重要になる場合があります。この操作はトライツリーと似ていますが、一部のエッジが複数の要素を使用する点が異なります。

次の疑似コードでは、これらのメソッドとメンバーが存在することを前提としています。

角

  • ノードターゲットノード
  • 文字列ラベル

ノード

  • エッジの配列エッジ
  • 関数isLeaf()
関数lookup(文字列x) { // 要素が見つからないルートから開始します。Node traverseNode := root ; int elementsFound := 0; // リーフが見つかるまで、または続行できない場合はトラバースしますwhile (traverseNode != null && !traverseNode.isLeaf() && elementsFound < x.length) { // x でまだ見つかっていない要素に基づいて、探索する次のエッジを取得します。Edge nextEdge := select edge from traverseNode.edges where edge.label is a prefix of x.suffix(elementsFound) // x.suffix(elementsFound) は、x の最後の (x.length - elementsFound) 要素を返します。// エッジは見つかりましたか？if (nextEdge != null ) { // 探索する次のノードを設定する traverseNode := nextEdge.targetNode; // エッジに格納されたラベルに基づいて見つかった要素を増分します elementsFound += nextEdge.label.length; } それ以外 { // ループを終了 traverseNode := null ; } } // リーフ ノードに到達し、ちょうど x.length 個の要素を使用した場合に一致が見つかります。return (traverseNode != null && traverseNode.isLeaf() && elementsFound == x.length); }

挿入

文字列を挿入するには、ツリーをそれ以上進めなくなるまで探索します。この時点で、入力文字列の残りのすべての要素でラベル付けされた新しい出力エッジを追加するか、残りの入力文字列と接頭辞を共有する出力エッジが既に存在する場合は、それを2つのエッジに分割し（最初のエッジには共通の接頭辞がラベル付けされます）、処理を続行します。この分割ステップにより、どのノードも文字列要素の数を超える数の子ノードを持たないことが保証されます。

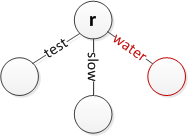
以下に挿入の例をいくつか示します。r は単にルートを表すことに注意してください。必要に応じて、エッジに空文字列のラベルを付けて文字列を終了できること、またルートには入力エッジがないことが前提となります。(上記の検索アルゴリズムは、空文字列のエッジを使用する場合は機能しません。)

  • ルートに「水」を挿入する
    ルートに「水」を挿入する
  • 「遅い」はそのままに「より遅い」を挿入する
    「遅い」はそのままに「より遅い」を挿入する
  • 「tester」の接頭辞である「test」を挿入します
    「tester」の接頭辞である「test」を挿入します
  • 「test」を分割して新しいエッジラベル「st」を作成しながら「team」を挿入します
    「test」を分割して新しいエッジラベル「st」を作成しながら「team」を挿入します
  • 「te」を分割し、前の文字列を1レベル下に移動しながら「toast」を挿入します。
    「te」を分割し、前の文字列を1レベル下に移動しながら「toast」を挿入します。

削除

文字列 x をツリーから削除するには、まず x を表すリーフノードを見つけます。次に、x が存在すると仮定して、対応するリーフノードを削除します。リーフノードの親ノードに他に子ノードが 1 つしかない場合、その子ノードの受信ラベルが親ノードの受信ラベルに追加され、子ノードが削除されます。

追加操作

  • 共通のプレフィックスを持つすべての文字列を検索します。同じプレフィックスで始まる文字列の配列を返します。
  • 先行文字列を検索: 辞書式順序に従って、指定された文字列より小さい最大の文字列を検索します。
  • 後続文字列を検索: 辞書式順序に従って、指定された文字列より大きい最小の文字列を検索します。

歴史

このデータ構造は1968年にドナルド・R・モリソン[ 6 ]とゲルノット・グヴェヘンベルガー[ 7 ]によって発明されました。

ドナルド・クヌースは、 『The Art of Computer Programming』第3巻498～500ページで、これらを「パトリシア木」と呼んでいます。これはおそらく、モリソンの論文のタイトルの頭字語「PATRICIA - 英数字でコード化された情報を取得するための実用的なアルゴリズム」に由来すると思われます。今日では、パトリシア木は基数が2の基数木と見なされています。これは、キーの各ビットが個別に比較され、各ノードが双方向（つまり、左対右）の分岐であることを意味します。

他のデータ構造との比較

(以下の比較では、キーの長さはkであり、データ構造にはn 個のメンバーが含まれていると想定しています。)

平衡木とは異なり、基数木では検索、挿入、削除がO(log n )ではなくO( k ) 時間で実行されます。通常k ≥ log nであるため、これは利点のようには思えませんが、平衡木ではすべての比較が文字列比較となり、最悪の場合でも O( k ) の時間を必要とします。この文字列比較の多くは、共通プレフィックスが長い（比較が文字列の先頭から始まる場合）ため、実際には遅くなります。トライでは、すべての比較に一定の時間がかかりますが、長さmの文字列を検索するにはm 回の比較が必要です。基数木では、これらの操作をより少ない比較で実行でき、必要なノードもはるかに少なくなります。

しかし、基数木にはトライと同様の欠点もあります。基数木は要素の文字列、または文字列への効率的な可逆マッピングを持つ要素にのみ適用できるため、全順序付けを持つあらゆるデータ型に適用されるバランス探索木のような完全な汎用性を備えていません。文字列への可逆マッピングは、バランス探索木に必要な全順序付けを生成するために使用できますが、その逆はできません。また、データ型が比較演算のみを提供し、シリアル化（または逆シリアル化）演算を提供しない場合にも、 この問題が発生する可能性があります。

ハッシュテーブルは一般的に挿入と削除にO(1)の時間がかかると言われていますが、これはキーのハッシュ計算が定数時間の処理であると仮定した場合のみ当てはまります。キーのハッシュを考慮すると、ハッシュテーブルは挿入と削除にO( k )の時間がかかると予想されますが、衝突の処理方法によっては最悪の場合、それ以上の時間がかかる可能性があります。基数木では、挿入と削除に最悪でもO( k )の時間がかかります。基数木の後続/先行操作もハッシュテーブルでは実装されていません。

変種

基数木の一般的な拡張では、「黒」と「白」の2色のノードが使用されます。指定された文字列が木に格納されているかどうかを確認するために、検索は木の最上部から開始され、入力文字列の端を辿り、それ以上進めなくなるまで続きます。検索文字列が消費され、最後のノードが黒ノードであれば検索は失敗、白ノードであれば検索は成功です。これにより、白ノードを用いて共通の接頭辞を持つ広範囲の文字列を木に追加し、その後、黒ノードを用いて少数の「例外」を空間効率の高い方法で挿入することで削除することが可能になります。

HATトライは、基数木に基づくキャッシュを考慮したデータ構造であり、効率的な文字列の保存と検索、そして順序付けされた反復処理を提供します。時間と空間の両方におけるパフォーマンスは、キャッシュを考慮したハッシュテーブルに匹敵します。[ 8 ] [ 9 ]

パトリシアトライは基数2（バイナリ）トライの特殊な変種であり、各キーのすべてのビットを明示的に格納するのではなく、ノードは2つのサブツリーを区別する最初のビットの位置のみを格納します。トラバーサル中に、アルゴリズムは検索キーのインデックスビットを調べ、必要に応じて左または右のサブツリーを選択します。パトリシアトライの注目すべき特徴は、格納された一意のキーごとに1つのノードを挿入するだけで済むため、パトリシアは標準的なバイナリトライよりもはるかにコンパクトであることです。また、実際のキーが明示的に格納されなくなったため、一致を確認するためにインデックス付きレコードに対して1回の完全なキー比較を実行する必要があります。この点で、パトリシアはハッシュテーブルを使用したインデックス作成に似ています。[ 6 ]

適応型基数木は、適応型ノードサイズを基数木に統合した基数木の変種です。通常の基数木の主な欠点の一つは、各レベルで一定のノードサイズを使用するため、空間を消費することです。基数木と適応型基数木の主な違いは、子要素の数に基づいて各ノードのサイズが可変であり、新しいエントリを追加するにつれて子要素のサイズも増加することです。したがって、適応型基数木は速度を低下させることなく、空間をより効率的に利用します。[ 10 ] [ 11 ] [ 12 ]

一般的な方法としては、親ノードがデータセット内の有効なキーを表す場合、子ノードを1つしか持たない親ノードを許容しないという基準を緩和することが挙げられます。この基数木は、内部ノードに少なくとも2つの子ノードのみを許容する基数木よりも高い空間効率を実現します。[ 13 ]

参照

参考文献

  1. ^ Morin, Patrick. 「文字列のデータ構造」(PDF) . 2012年4月15日閲覧。
  2. ^ "rtfree(9)" . www.freebsd.org . 2016年10月23日閲覧。
  3. ^カリフォルニア大学評議員会(1993). "/sys/net/radix.c" . BSD相互参照. NetBSD . 2019年7月25日閲覧.ルーティング検索のための基数ツリーを構築および維持するためのルーチン。
  4. ^ 「ロックレス、アトミック、汎用的なRadix/Patriciaツリー」 NetBSD 、 2011年。
  5. ^ Knizhnik, Konstantin.「Patricia Tries: プレフィックス検索のためのより優れたインデックス」、 Dr. Dobb's Journal、2008年6月。
  6. ^ a bモリソン、ドナルド・R・パトリシア -- 英数字でコード化された情報を取得するための実用的なアルゴリズム
  7. ^ G. Gwehenberger、 Anwendung einer binären Verweiskettenmethode beim Aufbau von Listen. Elektronische Rechenanlagen 10 (1968)、223–226 ページ
  8. ^ Askitis, Nikolas; Sinha, Ranjan (2007). HAT-trie: 文字列のためのキャッシュを考慮したトライベースデータ構造. 第62巻. pp.  97– 105. ISBN 978-1-920682-43-9。{{cite book}}:|journal=無視されました (ヘルプ)
  9. ^ Askitis, Nikolas; Sinha, Ranjan (2010年10月). 「スケーラブルでキャッシュ効率が高く、スペース効率の高い文字列のトライのエンジニアリング」. VLDB Journal . 19 (5): 633– 660. doi : 10.1007/s00778-010-0183-9 . S2CID 432572 . 
  10. ^ケンパー、アルフォンス;アイクラー、アンドレ (2013)。Datenbanksysteme、Eine Einführung。 Vol. 9.オルデンブール。ページ 604–605。ISBN​​ 978-3-486-72139-3。
  11. ^ "armon/libart: Cで実装されたAdaptive Radix Trees" . GitHub . 2014年9月17日閲覧。
  12. ^ Viktor Leis; et al. (2013). 「適応型基数木：メインメモリデータベースのためのARTfulインデックス」2013 IEEE 第29回国際データエンジニアリング会議 (ICDE) . pp.  38– 49. doi : 10.1109/ICDE.2013.6544812 . ISBN 978-1-4673-4910-9. S2CID  14030601 .
  13. ^有効なキーを表す Radix ツリーのノードは 1 つの子を持つことができますか?
ウィキメディア コモンズには、基数木に関連するメディアがあります。

実装

「 https://en.wikipedia.org/w/index.php?title=Radix_tree&oldid=1320228185#PATRICIA」から取得