プリズム（幾何学）

$一様なn$ 角柱プリズムの集合
一様なn角柱プリズムの集合
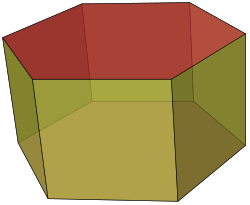	例: 均一な六角柱 ( n = 6 )
タイプ	半正多面体の意味で均一
面	2つのn辺の正多角形、; n 個の正方形
辺	3n
頂点	2n
オイラー特性	2
頂点配置	4.4. n
シュレーフリ記号	{ n }×{} ; t{2, n }
コンウェイ記法	P n
コクセター図
対称群	D n h , [ n ,2], (* n 22)、次数4 n
回転群	D n , [ n ,2] + , ( n 2 2 )、位数2 n
双対多面体	凸双一様 n角形両錐体
性質	凸、正多角形の面、等角、平行移動した底、辺⊥底
ネット
	例：一様九角柱のネット（n = 9）

n個の平行四辺形で接続された2つの平行なn角形底を持つ立体

幾何学において、プリズムとは、 $n$ 辺の多角形である底面、最初の底面を平行移動させた（回転せずに剛体的に移動させた）第 2 の底面、および2 つの底面の対応する辺を結んだ $n$ 面（必ずすべて平行四辺形）で構成される多面体である。底面に平行なすべての断面は、底面の平行移動である。プリズムは底面の名前にちなんで命名され、例えば五角形の底面を持つプリズムは五角柱プリズムと呼ばれる。プリズムはプリズマトイドのサブクラスである。^[2]

多くの基本的な幾何学用語と同様に、プリズム（ギリシャ語のπρίσμα （プリズマ） 「鋸で切ったもの」に由来）という言葉は、ユークリッドの『原論』で初めて用いられた。ユークリッドは『原論』第11巻でこの用語を「二つの向かい合う、等しく平行な平面で囲まれた立体図形で、残りは平行四辺形である」と定義した。しかし、この定義は、底辺の性質に関して十分に具体的ではないという批判を受けてきた（これが後代の幾何学研究者の間で混乱を招いた）。^[3]^[4]

斜プリズムと直プリズム

斜プリズムとは、接合する辺と面が底面に対して 垂直ではないプリズムです

例:平行六面体は、底面が平行四辺形である斜柱、または 6 つの平行四辺形の面を持つ多面体です。

直角柱とは、接合辺と接合面が底面に対して垂直である角柱のことです。 ^[5]これは、すべての接合面が直角である場合にのみ適用されます

直 $n$ 角柱の双対は直 $n$ 両錐体です。

正 $n$ 角形底面を持つ直方体（側面は長方形）は、シュレーフリ記号 ${}\times{n}で表されます。n$ $が$ 無限大に近づくにつれて、直方体は円筒に近づきます。^[6]

特殊なケース

直方体（底面が長方形）は、直方体、または非公式には長方形の箱とも呼ばれます。直方体には、シュレーフリ記号 ${}\times{}\times{}が付きます$
直角柱（底面が正方形）は、正方形直方体、または非公式に正方形の箱とも呼ばれます。

注: 一部のテキストでは、直方体柱または正方形柱という用語が、直方体柱と正方形柱の両方に使用されている場合があります。

種類

正角柱

正角柱とは、底面が正角である角柱のことです

一様柱

一様柱または半正柱は、規則的な底辺とすべての辺の長さが同じである直角柱です

したがって、一様なプリズムの側面はすべて正方形です。

したがって、一様プリズムのすべての面は正多角形である。また、そのようなプリズムは等角形であるため、一様多面体である。これらは半正多面体の無限列の2つのうちの1つを形成し、もう1つの列は反プリズムによって形成される。

一様な $n$ 角柱のシュレーフリ記号は $t{2, n}です。$

均一な n角柱の族ジョンソン立体 v t
プリズム名	二角プリズム	（三角柱）三角柱	（正方晶）四角柱	五角柱	六角柱	七角柱	八角柱	正六角柱	正十角柱	正十二角柱	正十二角柱	…	非正多面体プリズム
多面体画像												…
球面タイリング画像												平面タイリング画像
頂点設定	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	…	∞.4.4
コクセター図												…

性質

体積

プリズムの体積は、底面積と高さ、つまり 2 つの底面間の距離の積です(直角柱以外の場合、これは垂直距離を意味することに注意してください)。

したがって、音量は次のようになります。

V=Bh,

ここで、 $B$ は底面積、 $h$ は高さです。

したがって、辺の長さが $sである$ $n$ 辺の正多角形を底辺とする角柱の体積は次のようになります。 $V={\frac {n}{4}}hs^{2}\cot {\frac {\pi}{n}}.$

表面積

直方体の表面積は：

2B+Ph,

ここで、 $B$ は底面積、 $h は$ 高さ、 $P は$ 底辺の周囲長です。

したがって、辺の長さが $s$ 、高さが $hの正$ $n$ 角形を底面とする直角柱の表面積は次のようになります。

A={\frac {n}{2}}s^{2}\cot {\frac {\pi}{n}}+nsh.

対称性

$正底を$ 持つ直 $n$ 角柱の対称群は位数4nのDnhですが、立方体 $の$ $場合$ は $位$ $数$ 48のより大きな対称群 $Oh$ $を$ $持ち、これはD4hの3つのバージョン$ を部分群として持ち $ます$ 。回転群は $位$ $数2n$ の $Dn$ です $が$ 、立方体の場合は位数24のより大きな対称群 $O$ を持ち、これはD4の3つのバージョンを $部分$ $群$ として持ちます

対称群 $D n h$ $は、 nが偶数の場合$ にのみ反転を含みます。

細面体と二面体も二面体対称性を持ち、 $n$ 角形細面体の幾何学的切断、および $n$ 角形二面体の切詰めまたは拡大によって $n$ 角形プリズムを構築できます。

シュレーゲル図

P3	P4	P5	P6	P7	P8

相似多面体

切頂角柱

切頂角柱は、角柱をその底辺に平行でない平面で切断したときに形成される。切頂角柱の底辺は合同ではなく、辺は平行四辺形ではない。^[7]

ねじれたプリズム

ねじれプリズムは、各側面が正方形の対角線で二等分される均一な $n$ プリズムから、通常は（必ずしもそうである必要はないが）上面をねじることによって構成される非凸多面体である。 $π$ /nラジアン（⁠180 /n度）。二等分線が左に傾いている場合、上底を右方向（プリズムの上側から見て）に少しねじると非凸多面体になり、左方向にねじると凸多面体になります（画像のねじれた四角柱を参照）。二等分線が右に傾いている場合、上底を左方向にねじると非凸多面体になり、右方向にねじると凸多面体になります（ねじれた十二角柱を参照）。^[8]^[9]

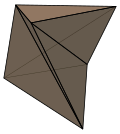
ねじれ角柱は、新たな頂点を追加しなければ四面体に分割できません。最も単純なねじれ角柱は三角形の底辺を持ち、シェーンハルト多面体と呼ばれます。

n角形ねじれプリズムは、 $n$ 角形一様反プリズムと位相的に同一ですが、対称群の半分、すなわち $D$ $n$ $, [$ $n$ $,2]$ $+$ , 位数 $2$ $n$ $を$ 持ちます。これは、三角形のペア間の四面体を削除した非凸反プリズムと見ることができます。任意のねじれ $n$ 角形プリズムは反プリズムであるため、図に示されているねじれ四角形プリズムとねじれ十二角形プリズムはどちらも反プリズムです。

3角形	4角形		12角形

シェーンハルト多面体	ねじれた四角柱	四角柱反プリズム	ねじれた十二角柱

錐台

錐台は、台形の側面と、上部と下部の異なるサイズの多角形を持つ、プリズムに似た構造です

星型プリズム

星型プリズムは、上下に2つの同一の星型多角形面があり、それらは平行で一定の距離だけずれ、長方形の面で接続された非凸多面体です。一様な星型プリズムは、シュレーフリ記号 ${p / q} \times {}$ で表され、 $p$ 個の長方形と2つの ${p / q}$ 面を持ちます。これは $p$ 角柱プリズムと位相的に同一です

例
${ }\times{ } 180 \times{ }$	$t a {3}\times{ }$		${5/2}\times{ }$	${7/2}\times{ }$	${7/3}\times{ }$	${8/3}\times{ }$
$D 2h$ 、注文番号8	$D 3h$ 、注文番号12		$D 5h$ 、注文番号20	$D 7h$ 、注文番号28		$D 8h$ 、注文番号32

交差プリズム

交差プリズムは、プリズムから構成される非凸多面体で、一方の底辺の頂点がこの底辺の中心を軸に反転（または180°回転）しています。これにより、側面の長方形の面が交差した長方形に変換されます。正多角形の底辺の場合、外観は $n$ 角形の砂時計です。すべての斜辺は単一の体心を通過します。注：この体心には頂点はありません。交差プリズムは、 $n$ 角形プリズムと位相的に同一です

例
${ }\times{ } 180 \times{ } 180$	$t a {3}\times{ } 180$		${3}\times{ } 180$	${4}\times{ } 180$	${5}\times{ } 180$	${5/2}\times{ } 180$	${6}\times{ } 180$
$D 2h$ 、注文番号8	$D 3d$ 、順序12			$D 4h$ 、注文番号16	$D 5d$ 、注文番号20		$D 6d$ 、順序24

ドーナツ型プリズム

ドーナツ型プリズムは、交差プリズムのような非凸多面体ですが、底面と上面がなく、多面体を閉じる単純な長方形の側面を持ちます。これは、偶数辺の底辺を持つ多角形でのみ可能です。これらは位相的トーラスであり、オイラー標数はゼロです。位相的多面体ネットは、2列の正方形タイリング（頂点配置 $4.4.4.4$ ）から切り取ることができます。これは、交差した長方形にそれぞれ接続された $n$ 個の正方形の帯です。n $角形$ ドーナツ型プリズムは、 $2n$ $個の$ 頂点、 $2n$ $個$ の面（ $n$ 個の正方形と $n個$ の交差した長方形）、および $4n$ $個$ の辺を持ちます。位相的に自己双対です

例
$D 4h$ 、注文番号16	$D 6h$ 、注文番号24
$V = 8$ 、 $E = 16$ 、 $F = 8$	$V = 12$ 、 $E = 24$ 、 $F = 12$

柱状多面体

柱状多面体は、柱の高次元化です。n $次元柱状多面体は、2つの($ $n$ $-1$ )次元多面体を次の次元に翻訳したものから構成されます

柱状 $n$ 多面体要素は ( $n - 1$ ) 多面体要素から 2 倍にされ、次に次の下位の要素から新しい要素が作成されます。

$F$ $i$ $i$ 面元( $i$ $= 0, ...,$ $n$ $) を持つn$ 多面体を考える。その ( $n$ $+ 1 ) 多面体プリズムは$ $2$ $F$ $i$ $+$ $F$ $i$ $-1$ $i$ 面元を持つ。(ただし $F$ $-1$ $= 0$ 、 $F$ $n$ $= 1$ とする。)

次元による：

$n$ 個の頂点と $n個の辺を持つ$ 多角形を考えます。その多角形は $2n$ $個の$ 頂点、 $3n$ $個$ の辺、 $2+$ $n$ 個の面を持ちます
$V$ 頂点、 $E$ 辺、 $F$ 面を持つ多面体を例に挙げましょう。そのプリズムには、 $2つの$ $V$ 頂点、 $2つの$ $E$ $+$ $V$ 辺、 $2つの$ $F$ $+$ $E$ 面、そして $2つの+$ $F$ セルがあります。
$V$ 頂点、 $E$ 辺、 $F$ 面、 $C$ セルを持つポリクロロンを考えます。そのプリズムには、 $2つの$ $V$ 頂点、 $2つの$ $E$ $+$ $V$ 辺、 $2つの$ $F$ $+$ $E$ 面、 $2つのC$ $+$ $F$ セル、 2つの $C$ $+$ $F$ ハイパーセルがあります。

一様柱状多面体

シュレーフリ記号 ${$ $p$ $,$ $q$ $,...,$ $t$ $}$ で表される正 $n多面体は$ 、2つのシュレーフリ記号{ $p$ $,$ $q$ $,...,$ $t$ $}\times{}$ の直積で表される一様柱状( $n$ $+$ $1 )多面体を形成できます$

次元による：

0 多面体プリズムは、空のSchläfli 記号 ${ }で表される$ 線分です。
1次元多面体プリズムは、2本の平行移動した線分から構成される長方形です。シュレーフリ記号 ${}\times{}の$ 積で表されます。正方形の場合、対称性は{}×{} = {4}と簡約されます $。$
例：、正方形、 ${}\times{}、$ 2つの平行線分、2つの線分辺で結ばれています
多角柱は、2つの多角形を平行移動させ、それらを長方形で結んで作られた3次元の柱です。正多角形 ${p}は、$ ${$ $p$ $}\times{}の積で表される一様なn$ 角柱を構成できます $。p$ $= 4$ の場合、正方形の辺が対称となるため、 ${4}\times{} = {4,3}の$ $立方体$ になります。
例：五角柱、 ${5}\times{}、$ 5つの長方形の辺でつながれた2つの平行五角形
多面体プリズムは、2つの多面体を平行移動させ、それらを3次元プリズムセルで連結した4次元プリズムです。正多面体 ${p, q}は、$ ${p, q$ }×{}の積で表される一様多面体プリズムを構築できます $。$ 多面体と各辺が立方体の場合、{ $4,3}\times{} = {4,3,3}の$ 四次元立方体となります。
例：、正十二面体柱、 ${5,3}\times{}、 12 個の五角柱の$ 側面で接続された2 つの平行な正十二面体。
…

高次のプリズム多面体は、任意の2つ以上の多面体の直積としても存在します。直積多面体の次元は、その要素の次元の和です。これらの最初の例は4次元空間に存在し、4次元における2つの多角形の積としてデュオプリズムと呼ばれます。

$正多角形プリズムは、 {p}\times{q}$ として表され、 $pq$ 頂点、 $2 pq$ 辺、 $pq$ 正方形面、 $p$ $q$ 角形面、 $q$ $p$ 角形面を持ち、 $p$ $q$ 角形プリズムと $q$ $p$ 角形プリズムで囲まれます。

たとえば、4-4 デュオプリズムの{4} $\times{4} は、$ 立方体プリズムの ${4,3}\times{ }$ と同様に、四次元立方体の対称性の低い形式です。 ${4}\times{4}\times{ }$ (4-4 デュオプリズムプリズム)、 ${4,3}\times{4}$ (立方体 - 4 デュオプリズム)、および ${4,3,3}\times{ } (四次元プリズム) は、$ 5 立方体の対称性の低い形式です。

参考文献

^ Johnson, N. W (2018). 「第11章有限対称群」.幾何学と変換. ケンブリッジ大学出版局. ISBN 978-1-107-10340-5。11.3 ピラミッド、プリズム、反プリズム、図11.3bを参照してください
^ グリュンバウム、ブランコ (1997)。「等角プリズマトイド」。離散幾何学および計算幾何学。18 : 13–52。土井: 10.1007/PL00009307。
^ マルトン、トーマス (1774). 『幾何学への王道：あるいは、簡単で親しみやすい数学入門』. 著者、販売. p. 360.
^ エリオット、ジェームズ (1845). 『実用幾何学と計測に関する完全論文集の鍵：規則の完全な解説を含む』ロングマン、ブラウン、グリーン、ロングマンズ. p. 3.
^ カーン, ウィリアム F.; ブランド, ジェームズ R. (1938).立体測量と証明. p. 28.
^ Geretschlager, Robert (2020). 競技を通して若い生徒を数学に取り組ませる：世界の視点と実践. 第1巻. World Scientific . p. 39. ISBN 978-981-120-582-8。
^ Kern & Bland (1938)、p. 81.
^ Gorini, Catherine A. (2003). The Facts on File: Geometry Handbook. Facts On File. p. 172. ISBN 0-8160-4875-4。
^ 「ねじれたプリズムの絵」

アンソニー・ピュー（1976年）『多面体：視覚的アプローチ』カリフォルニア州：カリフォルニア大学出版局バークレー校。ISBN 0-520-03056-7。第2章：アルキメデスの多面体、プリズマ、アンチプリズム

外部リンク

ワイスタイン、エリック・W.「プリズム」。MathWorld。
プリズムと反プリズムの紙製模型プリズムと反プリズムの無料ネット
ステラによって生成されたネットを使用したプリズムと反プリズムの紙モデル

[1] Johnson, N. W (2018). 「第11章有限対称群」.幾何学と変換. ケンブリッジ大学出版局. ISBN 978-1-107-10340-5。11.3 ピラミッド、プリズム、反プリズム、図11.3bを参照してください

[prismatoid-2] グリュンバウム、ブランコ (1997)。「等角プリズマトイド」。離散幾何学および計算幾何学。18 : 13–52。土井: 10.1007/PL00009307。

[malton-1774-3] マルトン、トーマス (1774). 『幾何学への王道：あるいは、簡単で親しみやすい数学入門』. 著者、販売. p. 360.

[elliot-1845-4] エリオット、ジェームズ (1845). 『実用幾何学と計測に関する完全論文集の鍵：規則の完全な解説を含む』ロングマン、ブラウン、グリーン、ロングマンズ. p. 3.

[mensuration-5] カーン, ウィリアム F.; ブランド, ジェームズ R. (1938).立体測量と証明. p. 28.

[cylinder-6] Geretschlager, Robert (2020). 競技を通して若い生徒を数学に取り組ませる：世界の視点と実践. 第1巻. World Scientific . p. 39. ISBN 978-981-120-582-8。

[FOOTNOTEKernBland193881-7] Kern & Bland (1938)、p. 81.

[gorini-2003-8] Gorini, Catherine A. (2003). The Facts on File: Geometry Handbook. Facts On File. p. 172. ISBN 0-8160-4875-4。

[9] 「ねじれたプリズムの絵」

$一様なn$ 角柱プリズムの集合
例: 均一な六角柱 ( $n = 6$ )
タイプ	半正多面体の意味で均一
面	$2つの n$ 辺の正多角形、 $n$ 個の正方形
辺	$3n$
頂点	$2n$
オイラー特性	2
頂点配置	$4.4. n$
シュレーフリ記号	${n}\times{}$ ^[1] $t{2, n}$
コンウェイ記法	$P n$
コクセター図
対称群	$D n h, [n,2], (* n 22)、$ 次数 $4 n$
回転群	$D n, [n,2] +, (n 2 2 )、$ 位数 $2 n$
双対多面体	凸双一様 $n$ 角形両錐体
性質	凸、正多角形の面、等角、平行移動した底、辺⊥底
ネット

例：一様九角柱のネット（ $n = 9$ ）