Rツリー
Rツリー
タイプ木
発明された1984
発明者アントニン・グットマン
ビッグO記法による時間計算量
手術平均最悪の場合
検索 O( log M n ) O( n ) [ 1 ]
入れる の上）
空間複雑性
2次元長方形のRツリーの簡単な例
ELKIを使用した 3D ポイントの R* ツリーの視覚化(直方体はディレクトリ ページです)

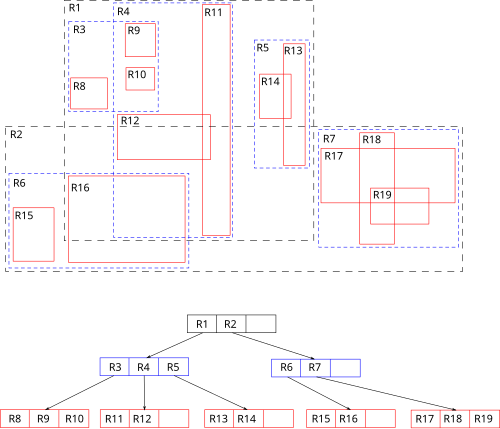
Rツリーは、空間アクセスメソッド、すなわち地理座標、長方形、多角形などの多次元情報のインデックス作成に使用されるツリーデータ構造です。Rツリーは1984年にアントニン・グットマンによって提案され[ 2 ]、理論と応用の両方の分野で重要な用途が見出されています[ 3 ]。Rツリーの一般的な実用例としては、レストランの場所や、典型的な地図を構成するポリゴン（道路、建物、湖の輪郭、海岸線など）などの空間オブジェクトを格納し、「現在地から2 km以内にあるすべての美術館を検索する」、「現在地から2 km以内にあるすべての道路セグメントを取得する」（ナビゲーションシステムに表示する）、「最寄りのガソリンスタンドを検索する」（ただし、道路は考慮しない）などのクエリに対する回答を迅速に見つけることが挙げられます。Rツリーは、大圏距離を含むさまざまな距離指標の最近傍探索[ 4 ]を高速化することもできます[ 5 ]。

Rツリーのアイデア

このデータ構造の核となる考え方は、近傍のオブジェクトをグループ化し、ツリーの上位レベルでそれらの最小の外接矩形で表現することです。Rツリーの「R」は矩形（rectangle）を表します。すべてのオブジェクトはこの外接矩形内に存在するため、外接矩形と交差しないクエリは、この矩形に含まれるオブジェクトと交差することはありません。リーフレベルでは、各矩形は単一のオブジェクトを表しますが、上位レベルでは、集約に含まれるオブジェクトの数が増加します。これは、データセットの近似が次第に粗くなっていくとも言えます。

B ツリーと同様に、R ツリーもバランスのとれた検索ツリー (すべてのリーフ ノードが同じ深さである) であり、データをページ内に整理し、ディスク上に保存するように設計されています (データベースで使用される)。各ページには最大数のエントリを含めることができ、多くの場合 と表記されます。また、最小充填量を保証します (ルート ノードを除く)。ただし、最小充填量が最大エントリ数の 30%～40% の場合に最高のパフォーマンスが得られます (B ツリーでは 50% のページ充填が保証され、B* ツリーでは 66% が保証されます)。その理由は、B ツリーに格納される線形データとは対照的に、空間データにはより複雑なバランス調整が求められるためです。 M{\displaystyle M}

ほとんどのツリーと同様に、検索アルゴリズム (交差、包含、最近傍検索など) はかなり単純です。重要なアイデアは、境界ボックスを使用してサブツリー内を検索するかどうかを決定することです。この方法では、ツリー内のほとんどのノードは検索中に読み込まれません。 B ツリーと同様に、R ツリーは、必要に応じてノードをメモリにページングでき、ツリー全体をメイン メモリに保持できない大規模なデータ セットやデータベースに適しています。データがメモリに収まる (またはキャッシュできる) 場合でも、オブジェクトの数が数百程度を超える場合は、ほとんどの実用的なアプリケーションで R ツリーを使用する方が、すべてのオブジェクトを単純にチェックするよりもパフォーマンス上の利点があります。ただし、インメモリ アプリケーションの場合は、パフォーマンスがわずかに優れているか、実際には実装が簡単な同様の代替手段があります。 コンピューティング ノードがネットワークで接続されているコンピューター クラスターで R ツリーのインメモリ コンピューティングを維持するために、研究者は RDMA (リモート ダイレクト メモリ アクセス) を使用して、分散環境でデータ集約型アプリケーションを R ツリーの下に実装しました。[ 6 ]このアプローチは、ますます大規模になるアプリケーションにスケーラブルであり、Rツリーに対して高いスループットと低レイテンシのパフォーマンスを実現します。

R ツリーの主な難しさは、一方ではバランスが取れていて (リーフ ノードが同じ高さである)、他方では長方形が空きスペースをあまり多くカバーせず、重なりすぎていない (検索中に処理する必要があるサブツリーが少なくなる) 効率的なツリーを構築することです。たとえば、効率的なツリーを取得するために要素を挿入する際の元々の考え方は、常にバウンディング ボックスの拡大が最小限で済むサブツリーに挿入するというものでした。そのページがいっぱいになると、データはそれぞれ最小限の領域をカバーする 2 つのセットに分割されます。R ツリーの研究と改良のほとんどは、ツリーの構築方法の改良を目的としており、効率的なツリーを最初から構築すること (バルク ローディングと呼ばれる) と、既存のツリーに変更を加えること (挿入と削除) という 2 つの目的にグループ化できます。

Rツリーは、最悪のケースで良好なパフォーマンスを保証するものではありませんが、一般的には現実世界のデータで良好なパフォーマンスを発揮します。[ 7 ] Rツリーの（バルクロードされた）Priority Rツリーバリアントは、最悪のケースに最適ですが、[ 8 ]複雑さが増すため、理論的な研究に限定されており、実際のアプリケーションではあまり注目されていません。

データがRツリーに編成されている場合、与えられた距離r内の近傍とすべてのポイントのk最近傍（任意のLp-ノルムに対して）は、空間結合を使用して効率的に計算できます。[ 9 ] [ 10 ]これは、 Local Outlier Factorなど、このようなクエリに基づく多くのアルゴリズムに役立ちます。DeLi-Clu、[ 11 ]密度リンククラスタリングは、同様の空間結合にRツリー構造を使用してOPTICSクラスタリングを効率的に計算するクラスター分析アルゴリズムです。

変種

アルゴリズム

データレイアウト

R ツリーのデータは、可変数のエントリ (定義済みの最大値まで、通常は最小値以上) を持つことができるページに編成されます。非リーフ ノード内の各エントリには、子ノードを識別する方法と、この子ノード内のすべてのエントリの境界ボックスという 2 つのデータが格納されます。リーフ ノードには、各子に必要なデータ (多くの場合、子を表すポイントまたは境界ボックスと、子の外部識別子) が格納されます。ポイント データの場合、リーフ エントリはポイントそのものです。ポリゴン データ (多くの場合、大きなポリゴンの格納が必要) の場合、一般的な設定では、ツリー内の一意の識別子とともにポリゴンの MBR (最小外接矩形) のみが格納されます。

Rツリーにおける検索プロセスは、フィルタと絞り込みの原則（FRP）に沿った2段階のアプローチを体現しています。この構造では、内部ノードはクエリと交差しない空間領域を迅速に除外する初期フィルタとして機能し、リーフノードは実際の空間オブジェクトを格納することで、洗練された正確な評価を提供します。

具体的には、範囲検索では、入力は検索長方形 (クエリ ボックス) です。検索はB+ ツリーでの検索とよく似ています。検索はツリーのルート ノードから始まります。すべての内部ノードには長方形のセットと対応する子ノードへのポインタが含まれ、すべてのリーフ ノードには空間オブジェクトの長方形が含まれます (何らかの空間オブジェクトへのポインタが存在する場合があります)。ノード内のすべての長方形について、検索長方形と重なるかどうかを判断する必要があります。重なる場合、対応する子ノードも検索する必要があります。検索は、重なり合うすべてのノードがトラバースされるまで、このように再帰的に実行されます。リーフ ノードに到達すると、含まれている境界ボックス (長方形) が検索長方形に対してテストされ、そのオブジェクト (存在する場合) が検索長方形内にある場合は結果セットに格納されます。

最近傍探索などの優先探索では、クエリは点または矩形で構成されます。ルートノードは優先キューに挿入されます。キューが空になるか、必要な数の結果が返されるまで、キュー内の最も近いエントリを処理して検索が続行されます。ツリーノードは展開され、その子ノードが再挿入されます。リーフエントリは、キュー内で見つかった時点で返されます。[ 12 ]このアプローチは、地理データの大圏距離など、さまざまな距離指標で使用できます。[ 5 ]

挿入

オブジェクトを挿入するには、ルートノードからツリーを再帰的に走査します。各ステップで、現在のディレクトリノード内のすべての長方形が検査され、拡大が最小限で済む長方形を選択するなどのヒューリスティックを用いて候補が選択されます。次に、このページを下り、リーフノードに到達します。リーフノードがいっぱいの場合は、挿入を行う前に分割する必要があります。ここでも、網羅的な検索はコストが高すぎるため、ヒューリスティックを用いてノードを2つに分割します。新しく作成されたノードを前のレベルに追加すると、このレベルが再びオーバーフローする可能性があり、これらのオーバーフローはルートノードまで伝播する可能性があります。このノードもオーバーフローすると、新しいルートノードが作成され、ツリーの高さが増加します。

挿入サブツリーの選択

アルゴリズムは、どのサブツリーに挿入するかを決定する必要があります。データオブジェクトが単一の矩形に完全に収まっている場合、選択は明確です。複数のオプションや拡大が必要な矩形がある場合、選択はツリーのパフォーマンスに大きな影響を与える可能性があります。

オブジェクトは、拡大が最小となるサブツリーに挿入されます。全体を通して混合ヒューリスティックが採用されています。次に、重複を最小化しようとします（重複が同数の場合は、まず拡大が最小、次に面積が最小となるものを優先します）。上位レベルではRツリーと同様の動作をしますが、同数の場合は、再び面積が小さいサブツリーを優先します。R *ツリーにおける長方形の重複の減少は、従来のRツリーに対する重要な利点の一つです。

オーバーフローノードの分割

あるノードのすべてのオブジェクトを2つのノードに再分配する場合、選択肢は指数関数的に増加するため、最適な分割方法を見つけるにはヒューリスティックを適用する必要があります。古典的なRツリーにおいて、GuttmanはQuadraticSplitとLinearSplitと呼ばれる2つのヒューリスティックを提案しました。QuadraticSplitでは、アルゴリズムは同一ノード内に存在すると最も不利な組み合わせとなる長方形のペアを検索し、それらを初期オブジェクトとして2つの新しいグループに配置します。次に、いずれかのグループに対する優先度が最も高いエントリ（面積増加の観点から）を検索し、すべてのオブジェクトが割り当てられるまで（最小充填率を満たすまで）、オブジェクトをこのグループに割り当てます。

分割戦略には他にも、Greene's Split [ 13 ] 、 R *-tree分割ヒューリスティック[ 14 ]（これも重複を最小化しようとしますが、2次ページを優先します）、AngとTan [ 15 ]が提案した線形分割アルゴリズム（ただし、非常に不規則な長方形が生成されるため、多くの現実世界の範囲およびウィンドウクエリではパフォーマンスが低下します）などがあります。R *-treeは、より高度な分割ヒューリスティックに加えて、ノードメンバーの一部を再挿入することでノードの分割を回避しようとします。これは、 B-treeがオーバーフローノードのバランスをとる方法に似ています。これにより重複も削減され、ツリーのパフォーマンスが向上することが示されています。

最後に、Xツリー[ 16 ]はR*ツリーの変種と見なすことができ、適切な分割が見つからない場合（特に高次元データの場合）、ノードを分割せずに、すべての追加エントリを含むいわゆるスーパーノードを構築することを決定することもできます。

米国の郵便番号データベースにおける異なる分割ヒューリスティックの影響
  • Guttman の二次分割。このツリー内のページは多くの部分で重複しています。
    ガットマンの二次分割。[ 2 ]このツリー内のページは多くの部分で重複しています。
  • Guttman の線形分割。構造はさらに悪いですが、構築も速くなります。
    ガットマンの線形分割。[ 2 ]さらに悪い構造だが、構築も速い。
  • グリーンの分割。ガットマンの戦略に比べてページの重複がはるかに少ない。
    グリーンの分割。[ 13 ]ページの重複はガットマンの戦略に比べてはるかに少ない。
  • Ang-Tan 線形分割。この戦略ではスライスされたページが生成され、多くの場合、クエリ パフォーマンスが低下します。
    Ang-Tan線形分割。[ 15 ]この戦略はスライスされたページを生成し、多くの場合クエリのパフォーマンスが低下します。
  • R*ツリーのトポロジカル分割。R*ツリーはページの重複を最小限に抑えようとするため、ページの重複は大幅に減少し、再挿入によってツリーがさらに最適化されます。分割戦略では2次ページが優先されるため、一般的なマップアプリケーションでより優れたパフォーマンスが得られます。
    R*ツリーのトポロジカル分割。[ 14 ] R*ツリーはページの重複を最小限に抑えようとするため、ページの重複は大幅に少なくなり、再挿入によってツリーがさらに最適化されます。分割戦略では2次ページが優先され、一般的なマップアプリケーションでより優れたパフォーマンスが得られます。
  • Sort-Tile-Recursive (STR) を用いてバルクロードされた R* ツリー。リーフページは全く重複せず、ディレクトリページもわずかにしか重複しません。これは非常に効率的なツリーですが、事前にデータを完全に把握しておく必要があります。
    Sort-Tile-Recursive (STR) を用いてバルクロードされたR* ツリー。リーフページは全く重複しておらず、ディレクトリページもわずかにしか重複していません。これは非常に効率的なツリーですが、事前にデータを完全に把握しておく必要があります。
  • M ツリーは R ツリーに似ていますが、ネストされた球形ページを使用します。ただし、これらのページの分割ははるかに複雑で、通常、ページの重複が多くなります。
    M木はR木に似ていますが、ネストされた球状ページを使用します。ただし、これらのページの分割ははるかに複雑で、ページの重複は通常はるかに大きくなります。

削除

ページからエントリを削除すると、親ページの境界矩形の更新が必要になる場合があります。ただし、ページが不足している場合、隣接するページとのバランスは取れません。代わりに、ページは解消され、そのすべての子（リーフオブジェクトだけでなく、サブツリーの場合もあります）が再挿入されます。この処理中にルートノードに要素が1つしかない場合、ツリーの高さが低くなる可能性があります。

一括読み込み

  • Nearest-X: オブジェクトは最初の座標 (「X」) で並べ替えられ、必要なサイズのページに分割されます。
  • Packed Hilbert R-tree : Nearest-X の派生形ですが、X 座標ではなく長方形の中心のヒルベルト値を使用してソートします。ページが重ならないという保証はありません。
  • ソート・タイル・リカーシブ（STR）：[ 17 ] Nearest-Xの別のバリエーションで、必要なリーフの総数を、これを達成するために必要な各次元の分割係数を と推定し、1次元ソートを用いて各次元を均等なサイズのパーティションに繰り返し分割します。結果のページが複数ページにわたる場合は、同じアルゴリズムを用いて再び一括ロードされます。ポイントデータの場合、リーフノードは重ならず、データ空間をほぼ均等なサイズのページに「タイル」状に分割します。l＝⌈オブジェクトの数/容量⌉{\displaystyle l=\lceil {\text{オブジェクトの数}}/{\text{容量}}\rceil }s＝⌈l1/d⌉{\displaystyle s=\lceil l^{1/d}\rceil }s{\displaystyle s}
  • 重複最小化トップダウン（OMT）：[ 18 ]スライス間の重複を最小限に抑え、クエリのパフォーマンスを向上させるトップダウンアプローチを使用したSTRの改良。
  • 優先度Rツリー

参照

参考文献

  1. ^ Rツリーcs.sfu.ca
  2. ^ a b c Guttman, A. (1984). 「R-Trees: 空間検索のための動的インデックス構造」(PDF) . 1984 ACM SIGMOD 国際データ管理会議 (SIGMOD '84) の議事録. p. 47. doi : 10.1145/602259.602266 . ISBN 978-0897911283. S2CID  876601 .
  3. ^ Y. Manolopoulos; A. Nanopoulos; Y. Theodoridis (2006). R-Trees: Theory and Applications . Springer. ISBN 978-1-85233-977-7. 2011年10月8日閲覧。
  4. ^ Roussopoulos, N.; Kelley, S.; Vincent, FDR (1995). 「最近傍クエリ」. 1995 ACM SIGMOD 国際データ管理会議 (SIGMOD '95 ) の議事録. p. 71. doi : 10.1145/223784.223794 . ISBN 0897917316。
  5. ^ a b Schubert, E.; Zimek, A.; Kriegel, HP (2013). 「地理データのインデックス作成のためのR木を用いた測地距離クエリ」.空間・時間データベースの進歩. コンピュータサイエンス講義ノート. 第8098巻. p. 146. doi : 10.1007/978-3-642-40235-7_9 . ISBN 978-3-642-40234-0。
  6. ^ Mengbai Xiao、Hao Wang、Liang Geng、Rubao Lee、Xiaodong Zhang (2022). 「クラスター上のRツリー向けRDMA対応インメモリコンピューティングプラットフォーム」 ACM Transactions on Spatial Algorithms and Systems. pp.  1– 26. doi : 10.1145/3503513 .{{cite conference}}: CS1 maint: 複数の名前: 著者リスト (リンク)
  7. ^ Hwang, S.; Kwon, K.; Cha, SK; Lee, BS (2003). 「メインメモリRツリーバリアントの性能評価」 .空間・時間データベースの進歩. コンピュータサイエンス講義ノート. 第2750巻. pp.  10. doi : 10.1007 /978-3-540-45072-6_2 . ISBN 978-3-540-40535-1。
  8. ^ Arge, L. ; De Berg, M. ; Haverkort, HJ ; Yi, K. (2004). 「Priority R-tree」（PDF） . 2004 ACM SIGMOD 国際データ管理会議（SIGMOD '04）の議事録. p. 347. doi : 10.1145/1007568.1007608 . ISBN 978-1581138597. S2CID  6817500 .
  9. ^ Brinkhoff, T.; Kriegel, H.P .; Seeger, B. (1993). 「R-treeを用いた空間結合の効率的な処理」. ACM SIGMOD Record . 22 (2): 237. CiteSeerX 10.1.1.72.4514 . doi : 10.1145/170036.170075 . S2CID 7810650 .  
  10. ^ Böhm, Christian; Krebs, Florian (2003-09-01). 「k近傍結合によるKDDアプリケーションのサポート」.データベースとエキスパートシステムのアプリケーション. コンピュータサイエンス講義ノート. 第2736巻. Springer, ベルリン, ハイデルベルク. pp.  504– 516. CiteSeerX 10.1.1.71.454 . doi : 10.1007/978-3-540-45227-0_50 . ISBN  9783540408062。
  11. ^ Achtert, Elke; Böhm, Christian; Kröger, Peer (2006). 「DeLi-Clu: 最近接ペアランキングによる階層的クラスタリングの堅牢性、完全性、有用性、効率性の向上」 Ng, Wee Keong; Kituregawa, Masaru; Li, Jianzhong; Chang, Kuiyu (編).知識発見とデータマイニングの進歩, 第10回太平洋アジア会議, PAKDD 2006, シンガポール, 2006年4月9日～12日, Proceedings . Lecture Notes in Computer Science. Vol. 3918. Springer. pp.  119– 128. doi : 10.1007/11731139_16 .
  12. ^ Kuan, J.; Lewis, P. (1997). 「R-tree family のための高速 k 最近傍探索」. ICICS 1997 国際情報通信信号処理会議議事録. テーマ: 情報システム工学と無線マルチメディア通信の動向 (カタログ番号 97TH8237) . p. 924. doi : 10.1109/ICICS.1997.652114 . ISBN 0-7803-3676-3。
  13. ^ a b Greene, D. (1989). 「空間データアクセス方式の実装と性能分析」. [1989] Proceedings. 第5回国際データ工学会議. pp.  606– 615. doi : 10.1109/ICDE.1989.47268 . ISBN 978-0-8186-1915-1. S2CID  7957624 .
  14. ^ a b Beckmann, N.; Kriegel, H.P .; Schneider, R.; Seeger, B. (1990). 「R*-tree: 点と矩形のための効率的かつ堅牢なアクセス手法」(PDF) . 1990 ACM SIGMOD 国際データ管理会議 (SIGMOD '90) の議事録. p. 322. CiteSeerX 10.1.1.129.3731 . doi : 10.1145/93597.98741 . ISBN  978-0897913652. S2CID  11567855 .
  15. ^ a b Ang, CH; Tan, TC (1997). 「R-treesのための新しい線形ノード分割アルゴリズム」. Scholl, Michel; Voisard, Agnès (編). Proceedings of the 5th International Symposium on Advances in Spatial Databases (SSD '97), Berlin, Germany, July 15–18, 1997 . Lecture Notes in Computer Science. Vol. 1262. Springer. pp.  337– 349. doi : 10.1007/3-540-63238-7_38 .
  16. ^ベルヒトルド, ステファン; ケイム, ダニエル A.;クリーゲル, ハンス＝ペーター(1996). 「X-Tree：高次元データのためのインデックス構造」 .第22回VLDBカンファレンス議事録. ムンバイ, インド: 28–39 .
  17. ^ Leutenegger, Scott T.; Edgington, Jeffrey M.; Lopez, Mario A. (1997年2月). 「STR: R木パッキングのためのシンプルで効率的なアルゴリズム」 .
  18. ^ Lee, Taewon; Lee, Sukho (2003年6月). 「OMT: R-treeのためのオーバーラップ最小化トップダウンバルクロードアルゴリズム」(PDF) .
  • ウィキメディア・コモンズのR-tree関連メディア
「 https://en.wikipedia.org/w/index.php?title=R-tree&oldid=1301628884」から取得