レスラーアトラクター

レスラーアトラクター

、、を伴うステレオグラムとしてのレスラーアトラクター${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=14}$

（r, log(z)）平面におけるロスラー力学による線分の折り畳み。カオス的な伸張と折り畳みの挙動を示す。、、${\displaystyle a=0.1}$ ${\displaystyle b=0.1}$ ${\displaystyle c=18}$

レスラーアトラクター（/ ˈ r ɒ s l ər /）は、 1970年代にオットー・レスラーが最初に研究した3つの非線形常微分方程式のシステムであるレスラーシステムのアトラクターです。 ^{[ 1 ] [ 2 ]}これらの微分方程式は、アトラクターのフラクタル特性に関連するカオスダイナミクスを示す連続時間力学システムを定義します。^{[ 3 ]}レスラーはそれをタフィー引き機の形式化として解釈しました。^{[ 4 ]}

レスラーシステムの一部の特性は、固有ベクトルなどの線形手法によって演繹できますが、システムの主な特徴には、ポアンカレ写像や分岐図などの非線形手法が必要です。オリジナルのレスラーの論文では、レスラーアトラクターはローレンツアトラクターと同様に動作するが、定性的に分析しやすいように意図されていたと述べられています。^{[ 1 ]}アトラクター内の軌道は、不安定な固定点の周りの平面に近い外向きの螺旋を描きます。グラフが十分に螺旋状になると、2つ目の固定点がグラフに影響を与え、次元の上昇とねじれを引き起こします。時間領域では、各変数が一定の値の範囲内で振動しているものの、その振動はカオス的であることが明らかになります。このアトラクターはローレンツアトラクターと類似点がありますが、より単純で、多様体は1つだけです。オットー・レスラーは1976年にレスラーアトラクターを設計したが^{[ 1 ]}、当初は理論的な方程式であったが、後に化学反応の平衡をモデル化するのに有用であることがわかった。 ${\displaystyle x,y}$ ${\displaystyle z}$

意味

レスラーシステムの定義式は以下の通りである: ^{[ 3 ]}

${\displaystyle {\begin{cases}{\frac {dx}{dt}}=-yz\\{\frac {dy}{dt}}=x+ay\\{\frac {dz}{dt}}=b+z(xc)\end{cases}}}$

レスラーは、、、およびを用いてカオスアトラクターを研究したが、それ以来、、、およびの特性はより一般的に用いられている。パラメータ空間の別の線は、位相解析を用いて研究された。これは、、、に対応し、分岐パラメータとして選択された。^{[ 5 ]}レスラーがこの方程式群をどのように発見したかは、レテリエとメッサーによって研究された。^{[ 6 ]}${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=5.7}$ ${\displaystyle a=0.1}$ ${\displaystyle b=0.1}$ ${\displaystyle c=14}$ ${\displaystyle b=2}$ ${\displaystyle c=4}$ ${\displaystyle a}$

安定性分析

${\displaystyle x,y}$ 、、を伴うレスラーアトラクターの平面${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=5.7}$

ロスラーアトラクターの優雅さの一部は、その方程式のうちの2つが線形であることによる。 を設定すると、平面 上の挙動を調べることができる。${\displaystyle z=0}$ ${\displaystyle x,y}$

${\displaystyle {\begin{cases}{\frac {dx}{dt}}=-y\\{\frac {dy}{dt}}=x+ay\end{cases}}}$

平面における安定性は、ヤコビ行列の固有値 を計算することで求めることができます。この固有値は です。このことから、 のとき、固有値は複素数で、両方とも正の実数成分を持つため、平面上で外向きの螺旋を持つ原点が不安定になることがわかります。次に、についてこの範囲の状況内で平面の挙動を考えてみましょう。したがって、より小さい限り、項は軌道を平面に近づけます。軌道がより大きくなるにつれて、-値は上昇し始めます。しかし、 が上昇するにつれて、の式における がの増加を止めます。 ${\displaystyle x,y}$ ${\displaystyle {\begin{pmatrix}0&-1\\1&a\\\end{pmatrix}}}$ ${\displaystyle (a\pm {\sqrt {a^{2}-4}})/2}$ ${\displaystyle 0<a<2}$ ${\displaystyle x,y}$ ${\displaystyle z}$ ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle x,y}$ ${\displaystyle x}$ ${\displaystyle c}$ ${\displaystyle z}$ ${\displaystyle z}$ ${\displaystyle -z}$ ${\displaystyle dx/dt}$ ${\displaystyle x}$

固定点

固定点を求めるために、3つのレスラー方程式をゼロに設定し、得られた方程式を解くことで各固定点の( , , )座標を決定した。これにより、各固定点座標の一般的な方程式が得られる。^{[ 7 ]}${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$

${\displaystyle {\begin{cases}x={\frac {c\pm {\sqrt {c^{2}-4ab}}}{2}}\\y=-\left({\frac {c\pm {\sqrt {c^{2}-4ab}}}{2a}}\right)\\z={\frac {c\pm {\sqrt {c^{2}-4ab}}}{2a}}\end{cases}}}$

これを使用して、特定のパラメータ値セットの実際の固定ポイントを表示できます。

${\displaystyle \left({\frac {c+{\sqrt {c^{2}-4ab}}}{2}},{\frac {-c-{\sqrt {c^{2}-4ab}}}{2a}},{\frac {c+{\sqrt {c^{2}-4ab}}}{2a}}\right)}$

${\displaystyle \left({\frac {c-{\sqrt {c^{2}-4ab}}}{2}},{\frac {-c+{\sqrt {c^{2}-4ab}}}{2a}},{\frac {c-{\sqrt {c^{2}-4ab}}}{2a}}\right)}$

上記の Rössler アトラクターの一般的なプロットに示されているように、これらの固定点の 1 つはアトラクター ループの中心にあり、もう 1 つはアトラクターから比較的離れたところにあります。

固有値と固有ベクトル

これらの固定点の安定性は、それぞれの固有値と固有ベクトルを決定することで分析できます。まずヤコビアンから始めます。

${\displaystyle {\begin{pmatrix}0&-1&-1\\1&a&0\\z&0&x-c\\\end{pmatrix}}}$

固有値は次の3次方程式を解くことで決定できます。

${\displaystyle -\lambda^{3}+\lambda^{2}(a+xc)+\lambda(ac-ax-1-z)+x-c+az=0\,}$

中心に位置する固定点の場合、Rössler の元のパラメータ値 a=0.2、b=0.2、c=5.7 から次の固有値が得られます。

${\displaystyle \lambda _{1}=0.0971028+0.995786i\,}$

${\displaystyle \lambda _{2}=0.0971028-0.995786i\,}$

${\displaystyle \lambda _{3}=-5.68718\,}$

負の固有値の大きさは、対応する固有ベクトルに沿った引力の強さを表します。同様に、正の固有値の大きさは、対応する固有ベクトルに沿った斥力の強さを表します。

これらの固有値に対応する固有ベクトルは次のとおりです。

${\displaystyle v_{1}={\begin{pmatrix}0.7073\\-0.07278-0.7032i\\0.0042-0.0007i\\\end{pmatrix}}}$

${\displaystyle v_{2}={\begin{pmatrix}0.7073\\0.07278+0.7032i\\0.0042+0.0007i\\\end{pmatrix}}}$

${\displaystyle v_{3}={\begin{pmatrix}0.1682\\-0.0286\\0.9853\\\end{pmatrix}}}$

中心固定点固有ベクトルの検査: 青い線は、、、およびで生成された標準のレスラーアトラクターに対応します。${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=5.7}$

、、を伴うロスラーアトラクター${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=5.7}$

これらの固有ベクトルには、いくつかの興味深い意味合いがあります。まず、2つの固有値/固有ベクトルのペア（と）は、アトラクターのメインディスクで発生する定常的な外向きの滑りを担っています。最後の固有値/固有ベクトルのペアは、多様体の中心を通る軸に沿って吸引し、アトラクター内で発生するZ方向の運動を説明しています。この効果は、下の図で大まかに示されています。 ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$

この図は、中心の固定点固有ベクトルを調べています。青い線は、、、およびで生成される標準的なロスラー アトラクターに対応します。このアトラクターの中心にある赤い点は です。その固定点と交差する赤い線は、およびによって生成される反発面を示しています。緑の線は、引き付ける を示しています。マゼンタの線は、わずかに上にある引き付ける固有ベクトル上の点から時間を逆方向にたどることによって生成されます。これは、そのベクトルによって完全に支配される点の動作を示しています。マゼンタの線は、固定点に向かって上方に引っ張られる前に、アトラクターの平面にほぼ接触していることに注意してください。これは、ロスラー アトラクターの全体的な外観と動作が、引き付ける平面と反発する平面との相互作用によって大きく左右されることを示しています。具体的には、ロスラー方程式から生成されたシーケンスが の周りをループし始め、ベクトルに向かって上向きに引っ張られ始め、ベクトルに向かってわずかに内側に曲がる曲線の上向きのアームを作成し、その後反発平面に向かって引っ張られて再び外側に押し出されることを意味します。 ${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=5.7}$ ${\displaystyle FP_{1}}$ ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$ ${\displaystyle v_{3}}$ ${\displaystyle FP_{1}}$ ${\displaystyle v_{3}}$ ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$ ${\displaystyle FP_{1}}$ ${\displaystyle v_{3}}$

外れ値の固定点の場合、Rössler の元のパラメータ値、、は次の固有値を生成します。 ${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=5.7}$

${\displaystyle \lambda_{1}=-0.0000046+5.4280259i}$

${\displaystyle \lambda_{2}=-0.0000046-5.4280259i}$

${\displaystyle \lambda _{3}=0.1929830}$

これらの固有値に対応する固有ベクトルは次のとおりです。

${\displaystyle v_{1}={\begin{pmatrix}0.0002422+0.1872055i\\0.0344403-0.0013136i\\0.9817159\\\end{pmatrix}}}$

${\displaystyle v_{2}={\begin{pmatrix}0.0002422-0.1872055i\\0.0344403+0.0013136i\\0.9817159\\\end{pmatrix}}}$

${\displaystyle v_{3}={\begin{pmatrix}0.0049651\\-0.7075770\\0.7066188\\\end{pmatrix}}}$

これらの固有値と固有ベクトルはレスラーアトラクター内に存在しますが、その影響は、初期条件がこの外れ値固定点の​​近傍にあるレスラー系の反復に限定されます。初期条件が と によって生成される吸引面上にある場合を除き、この影響は実質的に、結果として得られる系を一般的なレスラーアトラクターに向かって押し進めることになります。結果として得られる系列が中心固定点とアトラクター自体に近づくにつれて、この離れた固定点（およびその固有ベクトル）の影響は弱まります。 ${\displaystyle \lambda_{1}}$ ${\displaystyle \lambda_{2}}$

ポアンカレ地図

、、を伴うロスラーアトラクターのポアンカレ写像${\displaystyle a=0.1}$ ${\displaystyle b=0.1}$ ${\displaystyle c=14}$

ポアンカレ写像は、関数が特定の方向に設定された平面を通過するたびにその値をプロットすることで作成されます。一例としては、が負から正に変化する平面を関数が通過するたびに値をプロットすることが挙げられます。これは、ローレンツ アトラクターを調べるときによく行われます。レスラー アトラクターの場合は、レスラー方程式の性質により、写像は常に で平面と交差するため、平面は面白みがありません。 、、の平面では、ポアンカレ写像は、レスラー プロットの上昇およびねじれセクションから予想されるとおり、 が増加するにつれて値が上昇することを示します。この特定のポアンカレ プロット内の点の数は無限ですが、異なる値を使用すると、点の数は変化します。たとえば、値が 4 の場合、関数は周期 1 の周期軌道を生成するため、ポアンカレ マップ上には 1 つの点のみが存在し、値が 12.8 に設定されている場合、周期 6 の軌道に対応する 6 つの点が存在することになります。 ${\displaystyle y,z}$ ${\displaystyle x=0}$ ${\displaystyle x}$ ${\displaystyle x=0}$ ${\displaystyle x=0}$ ${\displaystyle z=0}$ ${\displaystyle x=0.1}$ ${\displaystyle a=0.1}$ ${\displaystyle b=0.1}$ ${\displaystyle c=14}$ ${\displaystyle z}$ ${\displaystyle x}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle c}$

ローレンツ写像

ローレンツ写像とは、軌道上の座標の連続する最大値間の関係です。アトラクター上の軌道を考え、そのx座標のn番目の最大値を とします。すると、散布図はほぼ曲線となり、を知ることで をほぼ正確に予測できることを意味します。^{[ 8 ]}${\displaystyle x_{max}(n)}$ ${\displaystyle x_{max}(n)}$ ${\displaystyle x_{max}(n+1)}$ ${\displaystyle x_{max}(n)}$ ${\displaystyle x_{max}(n+1)}$

a = 0.2、b = 0.2、c = 5 の Rössler アトラクターの Lorenz マップ。

局所最大値のマッピング

${\displaystyle Z_{n}}$ 対${\displaystyle Z_{n+1}}$

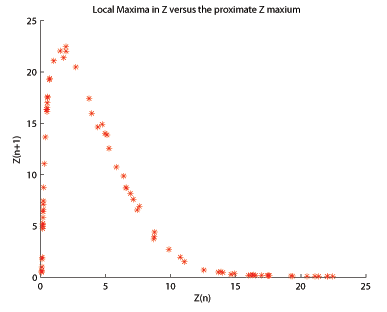
ローレンツアトラクターの原著論文^{[ 9 ]}で、エドワード・ローレンツはの極大値をその直前の極大値と比較して解析しました。視覚化すると、プロットはテントマップに似ており、マップとアトラクターの間で同様の解析を使用できることを示しています。レスラーアトラクターの場合、極大値を次の極大値に対してプロットすると、結果として得られるプロット (ここでは、、について表示) は単峰性になり、歪んだヘノンマップに似ています。レスラーアトラクターを使用して疑似 1 次元マップを作成できることから、同様の解析手法を使用できます。分岐図は特に便利な解析方法です。 ${\displaystyle z}$ ${\displaystyle z_{n}}$ ${\displaystyle z}$ ${\displaystyle z_{n+1}}$ ${\displaystyle a=0.2}$ ${\displaystyle b=0.2}$ ${\displaystyle c=5.7}$

パラメータの変化

レスラーアトラクターの挙動は、主に定数パラメータ、、の値に左右されます。一般的に、各パラメータを変化させると、系は周期軌道、不動点、または無限遠への脱出へと収束し、同様の効果が得られます。ただし、具体的な範囲や挙動はパラメータごとに大きく異なります。レスラー系の周期軌道、つまり「単位周期」は、ループの連続が繰り返されるまでに中心点の周りを回るループの数によって定義されます。 ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

分岐図は、レスラーアトラクターを含む力学系の挙動を解析するための一般的なツールです。分岐図は、システムの方程式を、1つを除くすべての変数を一定に保ち、最後の変数を変化させることによって作成されます。そして、過渡的要因が中和された後に、変化した変数の特定の値が訪れる点をグラフにプロットします。カオス領域は、プロットの塗りつぶされた領域で示されます。

変化させる

ここで、は0.2に固定され、は5.7に固​​定され、変化します。変化に対するアトラクターの挙動を数値的に検証すると、変化がアトラクターの挙動に不均衡な影響を与えることが示唆されます。分析結果は次のとおりです。 ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle a}$ ${\displaystyle a}$

• ${\displaystyle a\leq 0}$ : 中心に位置する固定点に収束する
• ${\displaystyle a=0.1}$ : 周期1の単位サイクル
• ${\displaystyle a=0.2}$ : ロスラーが選択した標準パラメータ値、カオス
• ${\displaystyle a=0.3}$ : カオス的アトラクター。メビウスの帯にかなり似ています（それ自体に折り重なります）。
• ${\displaystyle a=0.35}$ : .3に似ているが、ますます混沌としている
• ${\displaystyle a=0.38}$ : .35 と似ていますが、ますます混沌としています。

変動b

可変長のロスラーアトラクターの分岐図${\displaystyle b}$

ここで、は0.2に固定され、は5.7に固​​定され、は変化します。添付の​​図に示すように、 が0に近づくにつれてアトラクターは無限大に近づきます（ が非常に小さい値で上昇することに注意してください）。他のパラメータと比較して、 を変化させる と、周期3および周期6の軌道が発生する範囲が広がります。 および とは対照的に、の値が大きいほど、カオス状態ではなく周期1に収束します。 ${\displaystyle a}$ ${\displaystyle c}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle c}$ ${\displaystyle b}$

変化するc

可変長のロスラーアトラクターの分岐図${\displaystyle c}$

ここで、とが変化します。分岐図から、の値が小さい場合は周期的ですが、が増加すると急速にカオス状態になることがわかります。このパターンは が増加するにつれて繰り返されます。周期的な部分とカオス状態の部分が混在し、 が増加するにつれて高周期軌道に向かう傾向があります。例えば、周期1の軌道は の値が約4の場合にのみ現れ、分岐図では再び現れません。同じ現象が周期3でも見られます。 までは周期3の軌道が見られますが、それ以降は現れません。 ${\displaystyle a=b=0.1}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle c=12}$

値の範囲にわたって変化するアトラクターのグラフィカルな図は、これらすべてのパラメーター分析で見られる一般的な動作、つまり周期性と非周期性の間の頻繁な遷移を示しています。 ${\displaystyle c}$

変化するc

c = 4、周期1

c = 6、周期2

c = 8.5、周期4

c = 8.7、周期8

c = 9、混沌

c = 12、周期3

c = 12.6、周期6

c = 13、混沌

c = 18、混沌

c = 15.4、周期5

上記の画像セットは、過渡応答後のロスラーシステムにおける、をある範囲の値にわたって変化させたときの変化を示しています。これらの画像は を用いて生成されました。 ${\displaystyle c}$ ${\displaystyle a=b=.1}$

• ${\displaystyle c=4}$ 、周期1の軌道。
• ${\displaystyle c=6}$ 、周期2の軌道。
• ${\displaystyle c=8.5}$ 、周期4の軌道。
• ${\displaystyle c=8.7}$ 、周期8の軌道。
• ${\displaystyle c=9}$ 、スパースカオスアトラクター。
• ${\displaystyle c=12}$ 、周期3の軌道。
• ${\displaystyle c=12.6}$ 、周期6の軌道。
• ${\displaystyle c=13}$ 、スパースカオスアトラクター。
• ${\displaystyle c=15.4}$ 、周期5の軌道。
• ${\displaystyle c=18}$ 、塗りつぶされたカオスアトラクター。

周期軌道

アトラクターは周期軌道で密に満たされています。周期軌道 とは、 となる非零の値が存在する解です。これらの興味深い解は、ニュートン法を用いて数値的に導くことができます。周期軌道 は関数 の根であり、は時間発展、は恒等関数です。ダイナミクスの大部分は xy 平面で発生するため、周期軌道は投影後の中心平衡点の周りの 巻き数によって分類できます。${\displaystyle T}$ ${\displaystyle {\vec {x}}(t+T)={\vec {x}}(t)}$ ${\displaystyle \Phi _{t}-Id}$ ${\displaystyle \Phi _{t}}$ ${\displaystyle t}$ ${\displaystyle Id}$

巻数kによる周期軌道表

k =1

k = 2

k = 3

時間は実寸大ではありません。元のパラメータ(a,b,c) = (0.2,0.2,5.7)が使用されました。

数値実験から、すべての正の巻き数に対して、唯一の周期軌道が存在するように思われます。この退化の欠如は、おそらく問題の対称性の欠如に起因しています。アトラクターは、より理解しやすい不変多様体、すなわち1次元周期軌道と、周期軌道の2次元安定多様体および不安定多様体に分解できます。これらの不変多様体は、有理数が実数に対してそうであるように、アトラクターの自然な骨格です。

力学系理論の目的上、これらの多様体の位相不変量に興味があるかもしれない。周期軌道はに埋め込まれたのコピーであるため、その位相特性は結び目理論によって理解できる。巻き数1と2の周期軌道はホップリンクを形成し、これらの軌道を微分同相写像によって分離できないことを示している。 ${\displaystyle S^{1}}$ ${\displaystyle \mathbb {R} ^{3}}$

他のトピックへのリンク

レスラーアトラクターに見られる縞模様は、カントール集合を​​その中点を中心に回転させた形状に類似している。さらに、レスラーアトラクターに生じる半回転は、アトラクターの一部にしか影響を及ぼさない。レスラーは、彼のアトラクターが実際には「通常の帯」とメビウスの帯の組み合わせであることを示した。^{[ 10 ]}

参考文献

1. Rössler, OE (1976)、「連続カオスの方程式」、Physics Letters、57A (5): 397– 398、Bibcode : 1976PhLA...57..397R、doi : 10.1016/0375-9601(76)90101-8。
2. Rössler, OE (1979)、「ハイパーカオスの方程式」、Physics Letters、71A (2, 3): 155– 157、Bibcode : 1979PhLA...71..155R、doi : 10.1016/0375-9601(79)90150-6。
3. パイトゲン、ハインツ＝オットー; Jürgens, ハルトムート; Saupe、Dietmar ( 2004)、「12.3 The Rössler Attractor」、Chaos and Fractals: New Frontiers of Science 、Springer、 636–646ページ 。
4. レスラー、オットー E. (1983-07-01)。「混沌とした階層」。Zeitschrift für Naturforschung A。38 (7): 788–801 .土井: 10.1515/zna-1983-0714。ISSN 1865-7109。 
5. Letellier, C.; P. Dutertre; B. Maheu (1995). 「Rössler系の不安定周期軌道とテンプレート：体系的な位相的特徴づけに向けて」 . Chaos . 5 (1): 272– 281. Bibcode : 1995Chaos...5..271L . doi : 10.1063/1.166076 . PMID 12780181 . 
6. Letellier, C.; V. Messager (2010). 「オットー・E・レスラーのカオスに関する初期の論文への影響」. International Journal of Bifurcation and Chaos . 20 (11): 3585– 3616. Bibcode : 2010IJBC...20.3585L . doi : 10.1142/s0218127410027854 .
7. Martines-Arano, H.; García-Pérez, BE; Vidales-Hurtado, MA; Trejo-Valdez, M.; Hernández-Gómez, LH; Torres-Torres, C. (2019). 「細胞内Auナノ粒子におけるプラズモニック効果によって示されるカオス的特徴」 . Sensors . 19 (21): 4728. Bibcode : 2019Senso..19.4728M . doi : 10.3390/ s19214728 . PMC 6864870. PMID 31683534 .  
8. Olsen, Lars Folke; Degn, Hans (1985年5月). 「生物系におけるカオス」 . Quarterly Reviews of Biophysics . 18 (2): 165– 225. doi : 10.1017/S0033583500005175 . ISSN 1469-8994 . PMID 3912797 .  
9. Lorenz, EN (1963)、「決定論的非周期流」、J. Atmos. Sci.、20 (2): 130– 141、Bibcode : 1963JAtS...20..130L、doi : 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2。
10. レスラー、オットー E. (1976)。「単純な反応系におけるカオス的挙動」 . Zeitschrift für Naturforschung A。31 ( 3–4 ): 259–264 . Bibcode : 1976ZNatA..31..259R。土井：10.1515/zna-1976-3-408。

外部リンク

• PovRayを使ったFlashアニメーション
• ローレンツとレスラーのアトラクター2008年3月11日アーカイブポルトガル語ウェブアーカイブ – Javaアニメーション
• 3Dアトラクター: ロスラーとローレンツのアトラクターを3次元で視覚化して探索するMacプログラム
• Scholarpedia のレスラー アトラクター
• Rössler Attractor : 3D での数値インタラクティブ実験- experience.math.cnrs.fr- (javascript/webgl)