Rパリティ
特定の超対称モデルにおける離散対称性

Rパリティは素粒子物理学における概念である。極小超対称標準模型では、理論上のすべての繰り込み可能な結合において、重粒子数とレプトン数はもはや保存されない。重粒子数とレプトン数の保存性は非常に精密に検証されているため、実験データと矛盾しないためには、これらの結合は非常に小さくなければならない。Rパリティは、極小超対称標準模型（MSSM）の場に作用する対称性であり、これらの結合を禁じる。Rパリティは次のように定義される。[1] Z 2 {\displaystyle \mathbb {Z} _{2}} P R ＝ （ − 1 ） 3 B + L + 2 s {\displaystyle P_{\mathrm {R} }=(-1)^{3B+L+2s}}

あるいは、 P R ＝ （ − 1 ） 3 （ B − L ） + 2 s {\displaystyle P_{\mathrm {R} }=(-1)^{3(BL)+2s}}

ここで、 sはスピン、Bは重粒子数、Lはレプトン数です。標準模型のすべての粒子はRパリティが+1ですが、超対称粒子のRパリティは-1です。

パリティにはさまざまな形式があり、それぞれ効果と原理が異なるため、このパリティを他のパリティと混同しないように注意してください。

暗黒物質候補

Rパリティが保存されている場合、最も軽い超対称粒子（LSP ）は崩壊しません。したがって、この最も軽い粒子（もし存在するならば）は、一般に暗黒物質と呼ばれる宇宙の観測されていない質量を説明できる可能性があります。[2]観測結果に合わせるために、この粒子の質量は100  GeV/ c 2から1  TeV/ c 2 の粒子は中性で、弱い相互作用と重力相互作用のみで相互作用します。弱く相互作用する重い粒子、またはWIMPと呼ばれることもあります。

通常、MSSMにおける暗黒物質候補は電弱ゲージノとヒッグスノの混合体であり、ニュートラリーノと呼ばれます。MSSMの拡張では、スニュートリノを暗黒物質候補とすることも可能です。もう一つの可能​​性はグラビティーノで、これは重力相互作用のみで、厳密なRパリティを必要としません。

MSSMのRパリティを破る結合

MSSMの再正規化可能なRパリティ非保存結合は

  • ∫ d 2 θ λ 1 あなた c D c D c {\displaystyle \int d^{2}\theta \;\lambda _{1}\;U^{c}D^{c}D^{c}} Bに1単位違反する

この結合のみに関わる最も強い制約は、中性子-反中性子振動が観測されないことから生じます。

  • ∫ d 2 θ λ 2 質問 D c L {\displaystyle \int d^{2}\theta \;\lambda _{2}\;QD^{c}L} Lを1単位違反する

この結合のみに関係する最も強い制約は、クォークとレプトン荷電カレントの崩壊における フェルミ定数 の普遍性の違反です。 G F {\displaystyle G_{F}}

  • ∫ d 2 θ λ 3 L E c L {\displaystyle \int d^{2}\theta \;\lambda _{3}\;LE^{c}L} Lを1単位違反する

この結合のみに関わる最も強い制約は、レプトン荷電電流の崩壊におけるフェルミ定数の普遍性の違反です。

  • ∫ d 2 θ κ L H あなた {\displaystyle \int d^{2}\theta \;\kappa \;LH_{u}} Lを1単位違反する

この結合のみに関わる最も強い制約は、ニュートリノの質量が大きくなることです。

単一の結合に対する制約は十分に強いが、複数の結合が組み合わさると陽子崩壊につながる。したがって、陽子崩壊率の上限値から、結合値にもさらに上限値が求められる。

陽子崩壊

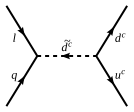
重粒子数とレプトン数が保存されず、Rパリティを破る結合を考慮しない場合、陽子は約10 −2 秒で崩壊するか、あるいは最小限のフレーバー違反を仮定すれば陽子の寿命は1年に延長される可能性がある。陽子の寿命は（崩壊経路によって異なるが）10 33 年以上から10 34 年と観測されているため、このモデルは非常に不利となる。Rパリティは、すべての繰り込み可能な重粒子数とレプトン数の破れの結合をゼロに設定し、陽子は繰り込み可能なレベルで安定し、陽子の寿命は10 32 年に延長され、これは現在の観測データとほぼ一致する。 お （ 1 ） {\displaystyle {\mathcal {O}}(1)}

陽子崩壊はレプトン数と重粒子数の両方の破れを伴うため、繰り込み可能なRパリティ破れの結合が陽子崩壊に至ることはまずありません。このことが、Rパリティ破れの結合のうち1組のみが非ゼロとなるRパリティ破れの研究の動機となっており、これは単一結合優勢仮説と呼ばれることもあります。

Rパリティの起源の可能性

R パリティを動機付ける非常に魅力的な方法は、現在の実験ではアクセスできないスケールで自発的に破れるB − L連続ゲージ対称性を用いることである。連続では、 BおよびLに違反する繰り込み可能な項が禁じられる。[3] [4] [5] [6]が、偶数の整数値3( B − L )をとるスカラー真空期待値 (またはその他の秩序パラメータ) によってのみ破れる場合、望ましい特性を持つ正確に保存される離散残留部分群が存在する。[7] [8] [9] [10] [11]重要な問題は、R パリティで奇数であるスニュートリノ(ニュートリノの超対称パートナー) が真空期待値を発現するかどうかを決定することである。現象論的根拠から、これが電弱スケールよりはるかに大きいスケールで破れる理論では起こり得ないことが示される。これは、大規模シーソー機構に基づくどの理論でも当てはまる。[12]結果として、そのような理論ではRパリティはすべてのエネルギーで正確のままである。 あなた （ 1 ） B − L {\displaystyle U(1)_{BL}} あなた （ 1 ） B − L {\displaystyle U(1)_{BL}} あなた （ 1 ） B − L {\displaystyle U(1)_{BL}}

この現象はSO(10) 大統一理論において自動対称性として現れる。Rパリティの自然な発生は、SO(10)では標準模型のフェルミオンが16次元スピノル表現から生じるのに対し、ヒッグスは10次元ベクトル表現から生じるため可能である。SO(10)不変結合を作るためには、スピノル場が偶数個でなければならない（つまり、スピノルパリティが存在する）。GUT対称性の破れ後、このスピノルパリティは、GUT対称性を破るためにスピノル場が使用されない限り、Rパリティに低下する。このようなSO(10)理論の明示的な例が構築されている。[13] [14]

参照

参考文献

  1. ^ Martin, SP (2011年9月6日). 「超対称性入門」.高エネルギー物理学の方向性に関する上級シリーズ. 18 : 1–98 . arXiv : hep-ph/9709356 . doi :10.1142/9789812839657_0001. ISBN  978-981-02-3553-6. S2CID  118973381。
  2. ^ Jungman, G.; Kamionkowski, M.; Griest, K. (1996). 「超対称暗黒物質」. Physics Reports . 267 ( 5–6 ): 195–373 . arXiv : hep-ph/9506380 . Bibcode :1996PhR...267..195J. doi :10.1016/0370-1573(95)00058-5. S2CID  119067698.
  3. ^ Mohapatra, RN (1986). 「超対称理論におけるニュートリノレス二重ベータ崩壊への新たな貢献」. Physical Review D. 34 ( 11): 3457– 3461. Bibcode :1986PhRvD..34.3457M. doi :10.1103/PhysRevD.34.3457. PMID  :9957083.
  4. ^ Font, A.; Ibáñez, LE; Quevedo, F. (1989). 「陽子の安定性は余分なZ0の存在を意味するのか？」(PDF) . Physics Letters B. 228 ( 1): 79– 88. Bibcode :1989PhLB..228...79F. doi :10.1016/0370-2693(89)90529-7.
  5. ^ Martin, SP (1992). 「ゲージ付きRパリティのためのいくつかの簡単な基準」. Physical Review D. 46 ( 7): R2769 – R2772 . arXiv : hep-ph/9207218 . Bibcode :1992PhRvD..46.2769M. doi :10.1103/PhysRevD.46.R2769. PMID  10015267. S2CID  14821065.
  6. ^ Martin, SP (1996). 「自然なRパリティ保存則を持つ超対称モデルの含意」. Physical Review D. 54 ( 3): 2340– 2348. arXiv : hep-ph/9602349 . Bibcode :1996PhRvD..54.2340M. doi :10.1103/PhysRevD.54.2340. PMID  10020912. S2CID  5751474.
  7. ^ Fayet, P. (1975). 「ヒッグス機構の超ゲージ不変拡張と電子およびニュートリノモデル」. Nuclear Physics B. 90 : 104–124 . Bibcode : 1975NuPhB..90..104F. doi :10.1016/0550-3213(75)90636-7.
  8. ^ Salam, A.; Strathdee, J. (1975). 「超対称性とフェルミオン数保存則」. Nuclear Physics B. 87 ( 1): 85– 92. Bibcode :1975NuPhB..87...85S. doi :10.1016/0550-3213(75)90253-9.
  9. ^ Farrar, GR; Weinberg, S. (1983). 「通常エネルギーにおける超対称性。II. R不変性、ゴールドストーンボソン、ゲージフェルミオン質量」. Physical Review D. 27 ( 11): 2732. Bibcode :1983PhRvD..27.2732F. doi :10.1103/PhysRevD.27.2732.
  10. ^ Fayet, P. (1977). 「自発的に破れた超対称性理論による弱相互作用、電磁相互作用、強相互作用」. Physics Letters B. 69 ( 4): 489– 494. Bibcode :1977PhLB...69..489F. doi :10.1016/0370-2693(77)90852-8.
  11. ^ Farrar, GR; Fayet, P. (1978). 「超対称性に関連する新しいハドロン状態の生成、崩壊、および検出の現象論」. Physics Letters B. 76 ( 5): 575. Bibcode :1978PhLB...76..575F. doi :10.1016/0370-2693(78)90858-4.
  12. ^ Aulakh, CS; Melfo, A.; Rašin, A.; Senjanović, G. (1998). 「超対称性と大規模左右対称性」. Physical Review D. 58 ( 11) 115007. arXiv : hep-ph/9712551 . Bibcode :1998PhRvD..58k5007A. doi :10.1103/PhysRevD.58.115007. S2CID  43296921.
  13. ^ Aulakh, CS; Bajc, B.; Melfo, A.; Rašin, A.; Senjanović, G. (2001). 「SO(10)理論によるRパリティとニュートリノ質量」Nuclear Physics B . 597 ( 1– 3): 89– 109. arXiv : hep-ph/0004031 . Bibcode :2001NuPhB.597...89A. doi :10.1016/S0550-3213(00)00721-5. S2CID  119100803.
  14. ^ Aulakh, CS; Bajc, B.; Melfo, A.; Senjanović, G.; Vissani, F. (2004). 「極小超対称大統一理論」. Physics Letters B. 588 ( 3–4 ) : 196– 202. arXiv : hep-ph/0306242 . Bibcode :2004PhLB..588..196A. doi :10.1016/j.physletb.2004.03.031. S2CID  119401374.
  • Barbier, R.; et al. (2005). 「Rパリティを破る超対称性」. Physics Reports . 420 ( 1–6 ): 1–195 . arXiv : hep-ph/0406039 . Bibcode :2005PhR...420....1B. doi :10.1016/j.physrep.2005.08.006.
  • 「R パリティ違反 ...」xstructure.inr.ac.ru。
  • 「Rパリティ違反…」FNAL。2010年5月28日時点のオリジナルよりアーカイブ。
「https://en.wikipedia.org/w/index.php?title=R-parity&oldid=1314552995」より取得