ラビ周波数

ラビ周波数は、振動する電磁場において、 2つの原子エネルギー準位の確率振幅が変動する周波数です。これは、2つの準位の遷移双極子モーメントと、電磁場の振幅（強度ではない）に比例します。このような2準位系の準位間のポピュレーション移動は、2つの準位間のエネルギー差と正確に共鳴する光で照射されると、ラビ周波数で発生します。入射光がこのエネルギー差（共鳴から）からずれると、ポピュレーション移動は一般化ラビ周波数で発生します。ラビ周波数は、原子を量子化されたエネルギー準位を持つ物体、電磁場を連続波として扱うため、半古典的な概念です。

核磁気共鳴実験において、ラビ周波数は、サンプルの正味核磁化ベクトルの無線周波数場を中心とした章動周波数です。（これは、静磁場を中心とした横方向核磁化の歳差運動を特徴付けるラーモア周波数とは異なることに注意してください。）

導出

ハミルトニアンを持つ量子システムの2 つのエネルギー固有状態を考えてみましょう(たとえば、これは水素原子やアルカリ原子のようなポテンシャル内の粒​​子のハミルトニアンです)。 ${\displaystyle {\hat {H}}_{0}}$ ${\displaystyle {\frac {1}{r}}}$

$${\displaystyle {\begin{aligned}\psi _{1}(\mathbf {r} ,t)&=e^{-i\omega _{1}t}|1\rangle \\\psi _{2}(\mathbf {r} ,t)&=e^{-i\omega _{2}t}|2\rangle \end{aligned}}}$$

それぞれ固有値とを持つ。時間依存ハミルトニアンを考える。 ${\displaystyle \hbar \omega _{1}}$ ${\displaystyle \hbar \omega _{2}}$

$${\displaystyle {\hat {\mathcal {H}}}={\hat {H}}_{0}+{\hat {V}}(t)}$$

ここで は電磁場のポテンシャルエネルギーである。ポテンシャルエネルギーを摂動として扱うと、摂動を受けたハミルトニアンの固有状態は、時間依存の係数を持つ元のハミルトニアンの固有状態が混ざったものになると予想される。 ${\displaystyle {\hat {V}}(t)=e\mathbf {r} \cdot \mathbf {E} _{0}\cos(\omega t)}$

$${\displaystyle \Psi (\mathbf {r} ,t)=c_{1}(t)e^{-i\omega _{1}t}|1\rangle +c_{2}(t)e^{-i\omega _{2}t}|2\rangle }$$

これを時間依存のシュレーディンガー方程式に代入すると

$${\displaystyle i\hbar {\frac {\partial \Psi (\mathbf {r} ,t)}{\partial t}}={\hat {\mathcal {H}}}\Psi (\mathbf {r} ,t)}$$

およびのそれぞれとの内積をとり、固有状態の直交条件を使用すると、係数およびの 2 つの方程式が得られます。 ${\displaystyle e^{i\omega _{1}t}\langle 1|}$ ${\displaystyle e^{i\omega _{2}t}\langle 2|}$ ${\displaystyle \langle i|j\rangle =\delta _{i,j}}$ ${\displaystyle c_{1}(t)}$ ${\displaystyle c_{2}(t)}$

$${\displaystyle {\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {c_{1}(t)\cos(\omega t)}{\hbar }}\langle 1|e\mathbf {r} \cdot \mathbf {E} _{0}|1\rangle +{\frac {e^{i\omega _{0}t}c_{2}(t)\cos(\omega t)}{\hbar }}\langle 1|e\mathbf {r} \cdot \mathbf {E} _{0}|2\rangle \\i{\dot {c}}_{2}(t)&={\frac {c_{2}(t)\cos(\omega t)}{\hbar }}\langle 2|e\mathbf {r} \cdot \mathbf {E} _{0}|2\rangle +{\frac {e^{-i\omega _{0}t}c_{1}(t)\cos(\omega t)}{\hbar }}\langle 2|e\mathbf {r} \cdot \mathbf {E} _{0}|1\rangle \end{aligned}}}$$

ここで、括弧内の2つの項は、電磁場の分極ベクトルに点在する双極子行列要素である。水素原子ポテンシャルの球対称な空間固有関数を考えると、対角行列要素はゼロとなり、以下の式が残る 。${\displaystyle \omega _{0}=\omega _{1}-\omega _{2}}$ ${\displaystyle |i\rangle }$

$${\displaystyle {\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {c_{2}(t)\cos(\omega t)}{\hbar }}\langle 1|e\mathbf {r} \cdot \mathbf {E} _{0}|2\rangle e^{i\omega _{0}t}\\i{\dot {c}}_{2}(t)&={\frac {c_{1}(t)\cos(\omega t)}{\hbar }}\langle 2|e\mathbf {r} \cdot \mathbf {E} _{0}|1\rangle e^{-i\omega _{0}t}\end{aligned}}}$$

または

$${\displaystyle {\begin{aligned}i{\dot {c}}_{1}(t)&=\Omega c_{2}(t)\cos(\omega t)e^{i\omega _{0}t}\\i{\dot {c}}_{2}(t)&=\Omega ^{*}c_{1}(t)\cos(\omega t)e^{-i\omega _{0}t}\end{aligned}}}$$

ここで、ラビ周波数はどこにありますか。 ${\displaystyle \オメガ :=\オメガ _{1,2}}$ ${\displaystyle \Omega _{i,j}={\frac {\langle i|e\mathbf {r} \cdot \mathbf {E} _{0}|j\rangle }{\hbar }}}$

直感

分子には遷移の遷移双極子モーメントが入ります。その振幅の二乗は電磁場と原子間の相互作用の強さを表し、 はベクトル電場振幅で、分極 を含みます。分子はエネルギーの次元を持つため、 で割ると角周波数 が得られます。 ${\displaystyle i\to j}$ ${\displaystyle \mathbf {E} _{0}={\hat {\epsilon }}E_{0}}$ ${\displaystyle \hbar}$

古典双極子との類推から、大きな双極子モーメントを持つ原子は電場による摂動を受けやすいことは明らかです。内積にはと​​いう因子が含まれます。ここでは光の偏光と遷移双極子モーメントの間の角度です。それらが平行のとき相互作用は最も強く、垂直のとき相互作用は全くありません。 ${\displaystyle \cos \theta}$ ${\displaystyle \theta}$

上記の微分方程式を書き直すと次のようになります。

$${\displaystyle {\begin{aligned}i{\dot {c}}_{1}(t)=\Omega c_{2}(t)\cos(\omega t)e^{i\omega _{0}t}&\to {\frac {\Omega c_{2}}{2}}(e^{i(\omega -\omega _{0})t}+e^{-i(\omega +\omega _{0})t})\\i{\dot {c}}_{2}(t)=\Omega ^{*}c_{1}(t)\cos(\omega t)e^{-i\omega _{0}t}&\to {\frac {\Omega ^{*}c_{1}}{2}}(e^{i(\omega +\omega _{0})t}+e^{-i(\omega -\omega _{0})t})\end{aligned}}}$$

回転波近似を適用すると、高周波振動項を無視することができるので、 ${\displaystyle \omega +\omega _{0}>>\omega -\omega _{0}}$

$${\displaystyle {\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {\Omega c_{2}}{2}}e^{i\delta t}\\i{\dot {c}}_{2}(t)&={\frac {\Omega ^{*}c_{1}}{2}}e^{-i\delta t}\end{aligned}}}$$

ここで、これはレーザーと原子の周波数間の離調と呼ばれます。 ${\displaystyle \delta =\omega -\omega _{0}}$

原子が（すなわち）の位置に あれば、これらの方程式を解くことで、${\displaystyle t=0}$ ${\displaystyle |1\rangle }$ ${\displaystyle c_{1}(0)=1}$

$${\displaystyle |c_{2}(t)|^{2}={\frac {\Omega ^{2}\sin ^{2}{\bigg (}{\frac {{\sqrt {\Omega ^{2}+\delta ^{2}}}t}{2}}{\bigg )}}{\Omega ^{2}+\delta ^{2}}}}$$

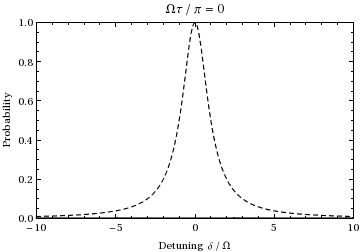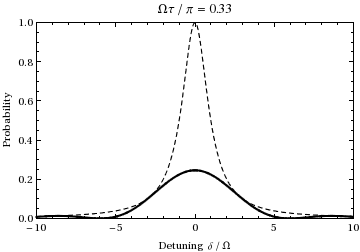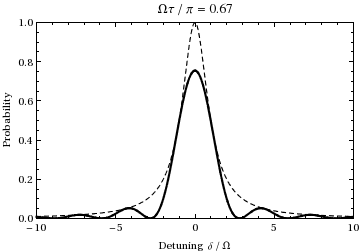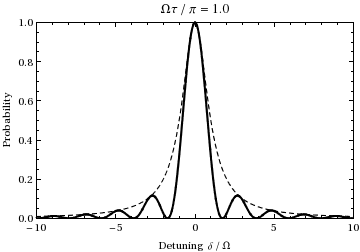
これは、状態 の集団の確率を、デチューンと時間の関数として表したものです。デチューンと時間を0から徐々に増加させたときの関数としてプロットすると、次のようになります。 ${\displaystyle |2\rangle }$ ${\displaystyle t={\frac {\pi }{\Omega }}}$

個体群はラビ周波数で 2 つの状態の間を振動する ことがわかります。${\displaystyle \delta =0}$

一般化ラビ頻度

この量は一般に「一般化ラビ周波数」と呼ばれます。 の場合、ラビフロッピングは実際にこの周波数で発生します。ここで、はデチューニングであり、遷移に対する光が共鳴からどれだけ離れているかを示す尺度です。例えば、上記のアニメーションをオフセット周波数 ±1.73 で調べると、アニメーション中に示されている 1/2 ラビサイクル（共鳴時）中に、振動は代わりに1サイクルを経ることがわかります。つまり、この式で予測されているように、（通常の）ラビ周波数 の2倍になります。また、入射光周波数が遷移周波数から遠ざかるにつれて、ラビ振動の振幅は減少します。これは、上記のグラフの破線の包絡線で示されています。 ${\displaystyle {\sqrt {\Omega ^{2}+\delta ^{2}}}}$ ${\displaystyle \delta \neq 0}$ ${\displaystyle \delta }$ ${\displaystyle \Omega _{i,j}}$

二光子ラビ周波数

コヒーレントラビ振動は、2光子遷移によっても駆動される可能性がある。この場合、3つの原子エネルギー準位、、、およびを持つ系を考える。ここで、は対応する周波数を持つ中間状態であり、2つの周波数成分を持つ電磁場である。 ${\displaystyle |1\rangle }$ ${\displaystyle |i\rangle }$ ${\displaystyle |2\rangle }$ ${\displaystyle |i\rangle }$ ${\displaystyle \omega _{i}}$

$${\displaystyle {\hat {V}}(t)=e\mathbf {r} \cdot \mathbf {E} _{L1}\cos(\omega _{L1}t)+e\mathbf {r} \cdot \mathbf {E} _{L2}\cos(\omega _{L2}t)}$$

二光子励起スキーム。左側に 、右側に が示されています。縦軸は周波数（またはエネルギー）軸です。${\displaystyle \omega _{i}\gg \omega _{2}>\omega _{1}}$ ${\displaystyle \omega _{2}>\omega _{i}>\omega _{1}}$

二光子遷移は、基底状態から中間状態への励起、そして中間状態から励起状態への励起とは異なります。原子は2つの光子を同時に吸収し、初期状態と終状態の間を直接遷移します。2つの光子のうなり音は、二光子遷移（初期状態と終状態間の周波数差）と共鳴する必要があります。

$${\displaystyle {\begin{aligned}&|\omega _{L1}-\omega _{L2}|=\omega _{2}-\omega _{1}\\&\Delta =|\omega _{L1}-(\omega _{i}-\omega _{1})|\gg 0\end{aligned}}}$$

デルタは中間状態からの散乱率を決定します。デルタが大きいほど、コヒーレンス時間は長くなります。

二光子ラビ周波数は、次の式に戻って導出できる。

$${\displaystyle {\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {\Omega _{1i}c_{i}}{2}}e^{i\Delta t}\\i{\dot {c}}_{i}(t)&={\frac {\Omega _{1i}^{*}c_{1}}{2}}e^{-i\Delta t}\end{aligned}}}$$

これらは基底状態と中間状態の間の励起を記述する。我々は解を知っている。

$${\displaystyle c_{i}(t)={\frac {\Omega _{1i}\sin {\bigg (}{\frac {{\tilde {\Omega }}_{1i}t}{2}}{\bigg )}}{{\tilde {\Omega }}_{1i}}}}$$

ここで、は初期状態から中間状態への遷移における一般化ラビ周波数である。同様に、中間状態から最終状態への遷移については、以下の式が成り立つ。 ${\displaystyle {\tilde {\Omega }}_{1i}}$

$${\displaystyle {\begin{aligned}i{\dot {c}}_{i}(t)&={\frac {\Omega _{i2}c_{2}}{2}}e^{i\Delta t}\\i{\dot {c}}_{2}(t)&={\frac {\Omega _{i2}^{*}c_{i}}{2}}e^{-i\Delta t}\end{aligned}}}$$

さて、上の式に代入すると${\displaystyle c_{i}(t)}$ ${\displaystyle {\dot {c}}_{2}(t)}$

$${\displaystyle i{\dot {c}}_{2}(t)={\frac {\Omega _{i2}^{*}\Omega _{1i}\sin {\bigg (}{\frac {{\tilde {\Omega }}_{1i}t}{2}}{\bigg )}}{2{\tilde {\Omega }}_{1i}}}e^{-i\Delta t}}$$

係数は次に比例します:

$${\displaystyle c_{2}(t)\propto {\frac {\Omega _{i2}\Omega _{1i}}{2\Delta }}}$$

これは2光子ラビ周波数である。^{[ 1 ]}これは、および遷移の個々のラビ周波数の積を、中間状態からの離調で割ったものである。 ${\displaystyle |1\rangle \to |i\rangle }$ ${\displaystyle |i\rangle \to |2\rangle }$ ${\displaystyle |i\rangle }$

参照

• ラビサイクル
• 真空ラビ振動
• ラビ共鳴法

参考文献

1. フット、クリストファー（2005年）『原子物理学』ニューヨーク：オックスフォード大学出版局、p.123、ISBN 0198506961。