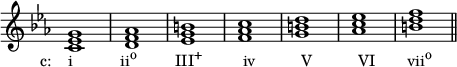ローマ数字分析

ハ長調におけるvi–ii–V–Iのコード進行。リードシートのコード名を用いると、これらのコードはAマイナー、Dマイナー、Gメジャー、Cメジャーと呼ばれる。^[1]

音楽理論において、ローマ数字分析は和音分析の一種であり、和音はローマ数字で表され、特定の音楽キー内での和音の度数と倍音機能をコード化します。

具体的な表記法は様々で、大文字の数字（例：I、IV、V）でメジャーコードを、小文字の数字（例：ii、iii、vi）でマイナーコードを表す理論家もいます。また、コードの品質に関わらず、すべてのコードに大文字の数字を使用する理論家もいます。^[2]（II、III、VIコードは常にマイナーコードであり、VIIコードは常に減音であるため、これ以上の区別は不要と考えられています。以下のメジャー・ダイアトニック・スケールの表を参照してください。）

ローマ数字は、楽曲の特定の調に依存せずに、楽曲の和声進行を記譜および分析するために使用できます。例えば、広く普及している12小節ブルース進行では、それぞれ第1度、第4度、第5度の音階に基づいて、トニック（I）、サブドミナント（IV）、ドミナント（V）のコードが用いられます。

歴史

ゴットフリート・ウェーバーによる、長音階と短音階の各度に用いられるローマ数字（左に三和音、右に七度）の説明。『音階芸術の理論』第2巻、45ページ。

ローマ数字分析は、和音は音符の一つ、つまりルート音で表し、名前を付けることができるという考えに基づいています（詳細は§ 歴史を参照）。このシステムは、ラモーの基音ベースの研究と著作から生まれたものです。

ローマ数字の最も初期の使用は、 1774 年にヨハン キルンベルガーの『ドイツの芸術家』の第 1 巻に見られます。^[3]その後間もなく、ゲオルグ ヨーゼフ フォーグラー修道院長は1778 年の『空軍音楽学校』で時折ローマ数字を使用しました。^[4]彼は著書『Handbuch zur』でもローマ数字について言及しました。 Harmonielehreは 1802 年に出版され、1806 年以降のいくつかの出版物ではローマ数字分析が採用されました。^[5]

ゴットフリート・ウェーバーの『音楽作曲理論』（1817-21）は、この手法を普及させたとよく言われる。より正確には、彼は長和音に大文字、短和音に小文字、減五度に上付き^{o 、長七度に破線7を用いる表記法を導入した（図参照）。 [6]}ウィーンの「度数理論」（Stufentheorie）の創始者とされるシモン・ゼヒターは、ローマ数字の使用を限定的に抑え、常に大文字を使用し、基本音はアルファベット表記やアラビア数字で表記することが多かった。^[7]シェーンベルクとシェンカーにこの理論を伝えたアントン・ブルックナーは、ウィーンでの授業ではローマ数字を使用しなかったようだ。^[8]

ローマ数字を体系的に使用した最初の著者は、ハインリヒ・シェンカーとアルノルド・シェーンベルクで、両者とも和声学の論文の中で使用しました。^[9]

一般的な数字

慣習期に由来する音楽理論では、ローマ数字は音階度やそれに基づく和音の指定によく用いられる。 ^[2]しかし、文脈によっては、キャレット付きのアラビア数字が音階度そのものの指定に用いられることもある（例：、、、…）。

教育テキストでよく使われる基本的なローマ数字分析記号を下の表に示します。^{[10] [11] : 71}

シンボル	意味	例
大文字のローマ数字	メジャートライアド	私
小文字のローマ数字	マイナートライアド	私
上付き文字^+	拡張三和音	私^+
上付き文字^o	減三和音	私^​
上付き数字	注記を追加	V7^​
2つ以上の数字( ^#-# )	連続して音符を追加（通常は中断）	^4～3節
上付き文字^#と^# #	最初の反転	私^6
	2番目の反転	私^6 4

以下に、C メジャー スケールの音符に基づいて構築された 7 つのルート ポジションの全音階三和音のローマ数字を示します。

さらに、『音楽理論と実践』によれば、「ベース音の上にシャープ、フラット、ナチュラルを示す必要がある場合がある」とある。^{[11] : 74}臨時記号は、上付き数字と下付き数字の下、上付き数字と下付き数字の前、またはスラッシュ（/）またはプラス記号（+）を使用して音程が上がっていることを示す（フラット調の♮または＃または＃）シャープ調の調号で。

二次コードはスラッシュで示されます (例: V/V)。

現代のシェンカー主義者は、シェンカー自身の用法に従って、すべてのモードのすべての度数に大文字の数字を使用することを好むことが多い。^[a]

ハインリヒ・シェンカー（1906年）による、J.S.バッハの無伴奏ヴァイオリンソナタ ハ長調 BWV1005のアレグロ・アッサイの13～15小節目の度数（Stufen ）のローマ数字分析。^[13]

反転

アラビア数字とラテン文字の両方を表すローマ数字分析の反転表記法。

ローマ数字は、コードの転回形を表すためにアラビア数字で補完されることがあります。このシステムは数字付き低音のシステムと似ており、アラビア数字はコードのベース音から上の特徴的な音程を表し、数字の3と5は通常省略されます。最初の転回形は数字の6で示されます（例：主音三和音の最初の転回形はI ⁶ですが、完全な転回形にはI 6が必要です）。⁶
₃）; 数字⁶
₄は第2転回形を表す（例：I⁶
₄転回7度和音も同様に、最も特徴的な音程、すなわち7度とルート音の間の2度音程を表す1つまたは2つのアラビア数字で表されます。V ⁷は属7度（例：G–B–D–F）です。V⁶
₅は第一転回形（B–D– F–G）であり、V⁴
₃その第2転回形（D– F–G –B）およびV⁴
₂またはV ²の3番目の転回形（F–G –B–D）。^{[11] ：79–80}

イギリスでは、ローマ数字とラテン文字を組み合わせて転回形を表す別のシステムが存在する。^[14]このシステムでは、「a」接尾辞は語根の位置、「b」は第一転回、「c」は第二転回を表す。しかし、「a」は語根の位置を表すためにほとんど使われない。⁵
₃アメリカの命名法では語根の位置を示すために使われることはほとんどない。^{[15] [検証失敗–議論を参照] [16] [17] [18]}

ジャズとポップスの数字

標準的な12小節ブルースのローマ数字分析

音楽理論、ジャズやポピュラー音楽向けのフェイクブックやリードシートでは、多くの曲や歌が調性に基づいて書かれており、すべてのコードには文字名と記号（例：C、G7、Dmなど）が与えられています^。一部のフェイクブックやリードシートでは、すべてのトライアドが大文字の数字で表され、その後にメジャーコードでない場合は記号が付きます（例：マイナーは「m」、ハーフディミニッシュは「^ø」、セブンスコードは「7」）。記号が付いていない大文字の数字はメジャーコードと解釈されます。ローマ数字を使用することで、リズムセクションの演奏者はバンドリーダーやリードシンガーが要求するあらゆる調で曲を演奏できます。伴奏者は、ローマ数字を特定の調で使用される特定のコードに翻訳します。

E メジャー キーでは、全音階コードは次のようになります。

• E ^maj7はI ^maj7（I ^∆7、または単にI）になります
• F ＃ m ⁷は II ^m7（または II ⁻⁷、 II ^min7、 IIm 、または II ⁻）になります
• G ＃ m ⁷は III ^m7（または III ⁻⁷、 III ^min7、 IIIm 、または III ⁻）になります。
• A ^maj7はIV ^maj7（IV ^∆7、または単にIVとも呼ばれる）になる
• B ⁷は V ⁷になります（または単に V、ジャズの文脈ではV ⁹または V ^{13 になることが多い）。}
• C ＃ m ⁷は VI ^m7（または VI ⁻⁷、 VI ^min7、 VIm 、または VI ⁻）となる。
• D ♯ ^ø7は VII ^ø7（または VII ^m7b5、 VII ^-7b5、または VII ^ø）になります

ポピュラー音楽やロック音楽では、長調の平行短調からコードを「借用」することがよく行われます。そのため、これらのジャンルでは、ホ長調では、ニ長調（または♭ VII）、ト長調（♭ III）、ハ長調（♭ VI）などのコードがよく使用されます。これらのコードはすべてホ短調から借用されています。同様に、短調でも平行長調からコードを「借用」することがあります。例えば、ホ短調では、4度音階で構築される全音階コードはIVm、つまりA短調です。しかし、実際には、ホ短調の多くの曲では、ホ長調から借用されたIV（A長調）が使用されています。しかし、短調で平行長調からコードを借用することは、それほど一般的ではありません。

V7またはVコード（Vドミナント7、またはVメジャー）の使用は、キーが長調か短調かを問わず、ほとんどのジャズやポップミュージックで一般的です。Vコードは短調の音階とは全音階的に一致しませんが、これらのスタイルで広く使用されているため、短調で使用することは通常「借用」とはみなされません。

全音階

メジャースケール

以下の表は、メジャースケールに基づいて構築されたコードのローマ数字を示しています。

スケール度	トニック	スーパートニック	中位数	サブドミナント	支配的な	下中音	リーディングトーン
慣例的な表記法	私	ii	iii	IV	V	6	7 ^o
代替表記	私	II	3	IV	V	6	VII [19]
コード記号	私はメジャー	2分	3分	IV メジャー	V Maj （またはV ^7）	VI分	VII dim (または VII ^o )

ハ長調では、これらのコードは

マイナースケール

以下の表は、ナチュラル・マイナー・スケールに基づいて構築されたコードのローマ数字を示しています。

スケール度	トニック	スーパートニック	中位数	サブドミナント	支配的な	下中音	サブトニック	リーディングトーン
慣例的な表記法	私	ii ^o	♭ III	iv	v	♭ VI	♭ VII	7 ^o
代替表記	私	ii	iii	iv	v	6	七
コード記号	私は分	II 薄暗い	♭ III Aug (または III Maj)	IV min （またはIV Maj）	V min （または V ^7）	♭ VI メジャー	♭ VII メジャー	VII dim (または VII ^o )

ハ短調（ナチュラルマイナー）では、これらのコードは

第七音階は、導音を形成するために半音上げることが非常に多く、属和音（V）は長和音（つまり、vマイナーではなくVメジャー） 、下音和音（vii）は減和音（つまり、 ♭ VIIではなくvii ^o）になります。このバージョンの短調スケールは、ハーモニック・マイナー・スケールと呼ばれます。これにより、作曲家は短調において、より強い終止の解決のために属和音（V）と属七和音（V7）の両方を利用でき、つまりVからiマイナーへと変化します。

モード

伝統的な記譜法では、7 つの現代旋法の 3 和音は次のようになります。

いいえ。	モード	トニック	スーパートニック	中位数	サブドミナント	支配的な	下中音	サブトニック/ リーディングトーン
1	イオニア語（主要）	私	ii	iii	IV	V	6	7 ^o
2	ドリアン	私	ii	♭ III	IV	v	vi ^o	♭ VII
3	フリギア	私	♭ II	♭ III	iv	v ^o	♭ VI	♭ vii
4	リディアン	私	II	iii	＃iv ^o​	V	6	七
5	ミクソリディアン	私	ii	iii ^o	IV	v	6	♭ VII
6	エオリアン（ナチュラルマイナー）	私	ii ^o	♭ III	iv	v	♭ VI	♭ VII
7	ロクリアン	私^​	♭ II	♭ iii	iv	♭ V	♭ VI	♭ vii

脚注

1. ストゥフェの記号として、ハ長調のローマ数字「I」は、長和音、短和音、第七和音、あるいはルートCによって制御される様々な音の組み合わせを表すことができます。また、同じローマ数字は、複数あるいは多数の和音を含む拡張パッセージの支配的な和声機能を表すこともできます。したがって、このシステムでは、1つの基本記号が構造的和声のあらゆる表現に適用され、数字付き低音の数字やその他の記号は基本型からの転回や逸脱を示します。…ローマ数字は、局所的な詳細を示すためではなく、より広範かつ分析的に、長調または短調のいずれかにおける和声機能を示すために使用できます。この方法は、両方の旋法における和音の質に関する十分な知識を前提としており、これは調号の認識と同じくらい基本的なスキルであると考えています。^[12]

参考文献

1. ウィリアム・G・アンドリュースとモリー・スクレイター（2000年）『西洋音楽資料集』第1部、227ページ。ISBN 1-55122-034-2。
2. ロジャー・セッションズ(1951). 『ハーモニック・プラクティス』 ニューヨーク: ハーコート・ブレース. LCCN  51-8476. p. 7.
3. ヨハン・フィリップ・キルンベルガー、Die Kunst des reinen Satzes、vol. I. ベルリンとケーニヒスベルク、デッカーとハルトゥング、1774 年、p. １５およびプレートはｐ． 19. ただし、キルンベルガーのローマ数字が目盛りの度数を表すのか、音程を表すのか（あるいはその両方）を表すのかは、完全には明らかではありません。
4. デイヴィッド・ダムシュローダー『ハーモニーを考える：分析の歴史的視点』ISBN 978-0-521-88814-1ケンブリッジ大学出版局、2008年、6ページ
5. Floyd K. Grave と Margaret G. Grave、「In Praise of Harmony: The Teachings of Abbé Georg Joseph Vogler」、Lincoln and London、University of Nebraska Press、1987 年、その他、pp. 70-71、169-170、および以下同様。
6. Gottfried Weber、Ver such einer geordneten Theorie der Tonsetzkunst、3d Edition、マインツ、ショット、1830–1832、vol. 2、44 ～ 63 ページ、§§ 151 ～ 158。
7. Simon Sechter、『Die Richtige Folge der Grundharmonien』、ライプツィヒ、ブライトコプフ ウント ヘルテル、全 3 巻、1853 ～ 1854 年。ローマ数字は 3 巻すべてに記載されています。
8. Anton Bruckner、 Vorlesungen über Harmonielehre und Kontrapunkt an der Universität Wien、E. Schwanzara ed.、Wien、Östrereichischer Bundesverlag、1950。 Robert E. Wason、ウィーン高調波理論、アルブレヒツベルガーからシェンカー、シェーンベルクまで、アナーバー、 UMIリサーチプレス、1982年。ISBN 0-8357-1586-867～84ページ。
9. ハインリヒ・シェンカー『 Harmonielehre』、シュトゥットガルト、ベルリン、コッタ、1906年；アルノルド・シェーンベルク『 Harmonielehre』、ウィーン、ユニバーサル、1911年。
10. エリック・テイラー (1989). 『AB音楽理論ガイド』第1巻. ロンドン: 英国王立音楽学校協会. pp.  60– 61. ISBN 1-85472-446-0。
11. ブルース・ベンワード、マリリン・ナディーン・セイカー (2003). 『音楽：理論と実践』 第1巻（第7版）. ボストン: マグロウヒル. ISBN 978-0-07-294262-0。
12. エドワード・アルドウェル、カール・シャクター、アレン・キャドワラダー (2011). 『ハーモニーとヴォイス・リーディング』（第4版）. シルマー, Cengage Learning. pp.  696– 697. ISBN 978-0-495-18975-6。
13. ハインリヒ・シェンカー、 Harmonielehre、シュトゥットガルト、ベルリン、コッタ、1906年、p. 186、例151。
14. ラブロック、ウィリアム (1981). 『音楽の基礎』ロンドン: ベル＆ハイマン. ISBN 0-7135-0744-6。
15. "musictheory.net". www.musictheory.net . 2020年11月29日閲覧。
16. Ben (2013年12月2日). 「コードの転回」.音楽理論アカデミー. 2020年12月6日閲覧。
17. ロブソン、エルシー・メイ（1960年代）『ハーモニー、メロディック・インヴェンション、オーケストラの楽器、音楽の形式』シドニー：ニコルソンズ。
18. Spearritt, Gordon (1995). Essential Music Theory . Melbourne: Allans Educational.
19. ジョン・メーガン(1989). 『音調とリズムの原理』 ジャズ・インプロヴィゼーション 第1巻（改訂増補版）. ニューヨーク: ワトソン・ガプティル. pp.  9– 16. ISBN 0-8230-2559-4。