フリップフロップ（電子機器）

SRラッチ（R1、R2 = 1  kΩ、R3、R4 = 10  kΩ）

電子工学において、フリップフロップとラッチは、状態情報を保存できる2つの安定状態を持つ回路、すなわち双安定マルチバイブレータです。この回路は、1つまたは複数の制御入力に印加される信号によって状態を変化させ、その状態（多くの場合、その論理和）を出力します。これは、シーケンシャルロジックにおける基本的な記憶素子です。フリップフロップとラッチは、コンピュータ、通信、その他多くのシステムで使用される デジタル電子システムの基本的な構成要素です。

フリップフロップとラッチは、1ビット（2進数）のデータを格納するデータ記憶素子として用いられます。2つの状態のうち、1つは「1」を、もう1つは「0」を表します。このようなデータ記憶は状態の記憶にも使用でき、このような回路は電子工学では順序論理と呼ばれます。有限状態機械（ステートマシン）で使用される場合、出力と次の状態は、現在の入力だけでなく、現在の状態（つまり、前の入力）にも依存します。また、パルスのカウントや、可変タイミングの入力信号を何らかの基準タイミング信号に同期させるためにも使用できます。

フリップフロップという用語は、歴史的には、ゲートを使用して1ビットのデータを格納するレベルトリガ（非同期、透過、または不透明）回路とエッジトリガ（同期、またはクロック）回路の両方を総称して指してきました。^{[ 1 ] [ 2 ]}現代の著者は、フリップフロップという用語をエッジトリガの記憶素子にのみ使用し、ラッチという用語をレベルトリガの記憶素子にのみ使用しています。 ^{[ 3 ] [ 4 ]}曖昧さを避けるために、「エッジトリガ」と「レベルトリガ」という用語が使用される場合があります。^{[ 5 ]}

レベル トリガー ラッチが有効になると透過的になりますが、エッジ トリガー フリップフロップの出力はクロック エッジ (正方向または負方向) でのみ変化します。

様々なタイプのフリップフロップとラッチが集積回路として提供されており、通常は1チップあたり複数の要素を備えています。例えば、74HC75は7400シリーズの4重透過型ラッチです。

歴史

1918年に出願されたエクルズとジョーダンのトリガーリレー特許の回路図。1つは正帰還経路を持つ増幅器のカスケードとして描かれ、もう1つは対称的なクロスカップルドペアとして描かれている。

最初の電子ラッチは1918年にイギリスの物理学者ウィリアム・エクルズとFWジョーダンによって発明された。^{[ 6 ] [ 7 ]}当初はエクルズ・ジョーダン・トリガー回路と呼ばれ、2つの能動素子（真空管）で構成されていた。^{[ 8 ]}この設計は1943年のイギリスの暗号解読コンピュータ「コロッサス」で使用されており^{[ 9 ]} 、このような回路やそのトランジスタ版は集積回路の導入後もコンピュータで一般的に使用されていたが、現在では論理ゲートで作られたラッチやフリップフロップも一般的になっている。^{[ 10 ] [ 11 ]}初期のラッチはトリガー回路やマルチバイブレータなどと呼ばれていた。

米国ジェット推進研究所の技師、P.L.リンドリーによると、以下に詳述するフリップフロップのタイプ（SR、D、T、JK）は、1954年にカリフォルニア大学ロサンゼルス校（UCLA）で行われたコンピュータ設計の講義でモンゴメリー・フィスターが初めて取り上げ、その後、彼の著書『デジタルコンピュータの論理設計』に登場した。^{[ 12 ] [ 13 ]}リンドリーは当時、ヒューズ・エアクラフト社でエルドレッド・ネルソンの下で働いていた。ネルソンは、両方の入力がオン（論理「1」）のときに状態が変化するフリップフロップにJKという用語を作り出した。その他の名前はフィスターによる造語である。これらは、以下に示す定義の一部と若干異なる。リンドリーは、ヒューズ・エアクラフト社で働いていた当時、この用語を作り出したエルドレッド・ネルソンからJKフリップフロップの話を聞いたと説明している。当時ヒューズ社で使用されていたフリップフロップはすべて、JKとして知られるようになったタイプであった。ネルソンは論理システムを設計する際に、フリップフロップの入力に次のように文字を割り当てた：#1: A & B、#2: C & D、#3: E & F、#4: G & H、#5: J & K。ネルソンは1953年に提出された特許出願で「j入力」と「k入力」という表記を使用した。 ^{[ 14 ]}

実装

バイポーラ接合トランジスタに基づく透明ラッチ回路

透過ラッチまたは非同期ラッチは、交差結合された反転素子の 1 組を中心に構築できます。実際の回路では、真空管、バイポーラ トランジスタ、電界効果トランジスタ、インバータ、反転論理ゲートなどが使用されています。

クロックド・フリップフロップは同期システム向けに特別に設計されており、専用のクロック信号（クロッキング、パルシング、またはストローブと呼ばれる）の遷移時を除き、入力を無視します。クロッキングにより、フリップフロップは遷移時の入力信号の値に基づいて出力信号を変化させるか、または保持します。フリップフロップの中には、クロックの 立ち上がりエッジで出力を変化させるものもあれば、立ち下がりエッジで出力を変化させるものもあります。

基本的な増幅段は反転増幅であるため、2段を連続的に（カスケード接続して）接続することで、必要な非反転増幅器を構成できます。この構成では、各増幅器は、他方の反転増幅器に対する能動的な反転帰還回路と見なすことができます。したがって、回路図は通常、対称的なクロスカップルドペアとして描かれますが、2段は非反転ループに接続されています（どちらの図も、Eccles-Jordan特許で初めて紹介されました）。

種類

フリップフロップとラッチは、SR（セット・リセット）、D（データ）、T（トグル）、JK （上記の歴史セクションを参照）という一般的なタイプに分類できます。特定のタイプの動作は、入力信号および／または現在の出力に基づいて「次の」出力（ Q _next）を導く特性方程式によって記述できます。 ${\displaystyle Q}$

非同期セット・リセットラッチ

静的ゲートを構成要素として使用する場合、最も基本的なラッチは非同期セットリセット (SR) ラッチです。

2つの入力SとRは、S=1とR=0の組み合わせで内部状態を1に設定し、S=0とR=1の組み合わせで内部状態を0にリセットすることができます。^{[注 1 ]}

SRラッチは、クロスカップルされたNORまたはNAND論理ゲートのペアで構成できます。格納されたビットはQでマークされた出力に現れます。

NAND、NOR、AND、ORは制御された演算と考えると分かりやすい。つまり、一方の入力が制御入力セットとして選択され、もう一方のビットが制御状態に応じて処理される入力として選択される。そして、これらのゲートはすべて、入力(x)を無視して定数値を出力する制御値と、入力を通過させる制御値（場合によっては補数）を持つ。

${\displaystyle {\begin{aligned}\operatorname {NAND} (x,0)&=1&\operatorname {NAND} (x,1)&={\bar {x}}\\\operatorname {NOR} (x,0)&={\bar {x}}&\operatorname {NOR} (x,1)&=0\\\operatorname {AND} (x,0)&=0&\operatorname {AND} (x,1)&={x}\\\operatorname {OR} (x,0)&=x&\operatorname {OR} (x,1)&=1\\\end{aligned}}}$

基本的に、これらはすべて、特定の値を設定するか、入力値を通過させるスイッチとして使用できます。

SR NORラッチ

クロスカップルされたNORゲートのペアから構成されるSRラッチのアニメーション。赤と黒はそれぞれ論理「1」と「0」を意味します。

アニメーション化されたSRラッチ。黒と白はそれぞれ論理「1」と「0」を意味します。

1. S = 1、R = 0: 設定
2. S = 0、R = 0: ホールド
3. S = 0、R = 1: リセット
4. S = 1、R = 1: 許可されません

制限された組み合わせ（D）から（A）に移行すると不安定な状態になります。

SR NORラッチは、図に示すように、2つの並列NORゲートで構成され、各NORの出力は、もう一方のNORの1つの入力にもファンアウトされます。これらの出力と入力の接続をフィードバック入力、または単にフィードバックと呼びます。残りの入力は、上で説明したように制御入力として使用します。この時点ではすべてが対称的であるため、出力がどの入力に接続されているかは問題ではないことに注意してください。ここで、残りの制御入力のどれをセットおよびリセットとして使用するかを選択することで対称性を破り、セット制御付きのNORゲートを「セットNOR」、リセット制御付きのNORを「リセットNOR」と呼ぶことができます。図では、セットNORが下、リセットNORが上にあります。リセットNORの出力は格納ビットQになり、セットNORの出力にはその補数Qが格納されます。

SR NORラッチの動作を導出するには、SとRを制御入力とみなし、上記の式から、制御1でセットおよびリセットNORを入力とすると出力が0に固定され、制御0でセットおよびリセットNORを入力とするとNOTゲートとして動作することに注意してください。これにより、SRラッチの動作を単純な条件として導出することが可能になります（例えば、各行に値を割り当てて、それらがどのように伝播するかを確認する代わりに）。

• RとSが両方ともゼロの場合、R NORとS NORはどちらも単に出力の補数となるフィードバックを課すだけです。これは、出力が互いに補数である限り満たされます。したがって、出力QとQは、Q=0でもQ=1でも、一定の状態に維持されます。
• S=1でR=0の場合、セットNORはQ =0を固定し、リセットNORはQ=1に適応します。Sがゼロに戻されると、値は上記のように維持されます。
• 同様に、R=1でS=0の場合、リセットNORはQ=0を固定し、セットNORはQ = 1を適応させます。Rを0に戻すと、状態は維持されます。
• R=S=1 の場合、NOR は両方の出力を 0 に固定しますが、これは補数値を格納する有効な状態ではありません。

SRラッチ動作^{[ 5 ]}

特性表				励起テーブル
S	R	Q次へ	アクション	質問	Q次へ	S	R
0	0	質問	保留状態	0	0	0	X
0	1	0	リセット	0	1	1	0
1	0	1	セット	1	0	0	1
1	1	X	許可されていません	1	1	X	0

注: X は「don't care」を意味します。つまり、0 または 1 のいずれかが有効な値です。

R = S = 1 の組み合わせは、両方の NOR ゲートがゼロを出力するため、論理方程式 Q = not Qが破れるため、制限組み合わせまたは禁制状態と呼ばれます。また、この組み合わせは、両方の入力が同時にローになる可能性のある回路（つまり、制限状態からホールド状態への遷移）には適していません。出力は準安定状態のままになり、ゲート間の伝播時間関係に応じて最終的に 1 または 0 に固定される可能性があります（競合状態）。

SR NORラッチの仕組み

制限された組み合わせを克服するには、入力にゲートを追加して、(S, R) = (1, 1)制限されていない組み合わせのいずれかに変換することができます。具体的には、次のようなゲートです。

• Q = 1 (1, 0) – S（優勢）ラッチと呼ばれる
• Q = 0 (0, 1) – R（優勢）ラッチと呼ばれる

これはほぼすべてのプログラマブル ロジック コントローラで実行されます。

• ホールド状態（0, 0） – Eラッチと呼ばれる

あるいは、制限された組み合わせで出力を切り替えることもできます。その結果、 JKラッチが生成されます。

SR ラッチの特性方程式は次のとおりです。

${\displaystyle Q_{\text{next}}={\bar {R}}Q+{\bar {R}}S}$ または^{[ 15 ]}${\displaystyle Q_{\text{next}}={\bar {R}}(Q+S).}$

ここで、A + Bは（AまたはB）を意味し、ABは（AかつB）を意味します。

別の表現は次のとおりです。

${\displaystyle Q_{\text{next}}=S+{\bar {R}}Q}$ ^{[ 16 ]}と${\displaystyle SR=0}$

SR NANDラッチ

クロスカップルドNANDゲートから構成されるSRラッチ

以下に示す回路は基本的なNANDラッチです。入力は通常、それぞれセット（S ） 、リセット（ R）として表されます。NAND入力は通常、ラッチ動作に影響を与えないように論理1でなければならないため、この回路では入力は反転（またはアクティブロー）されているとみなされます。

この回路はSR NORと同じフィードバック回路を使用していますが、NORゲートをNANDゲートに置き換えただけで、制御入力信号が変化した後でも論理状態を「記憶」して保持します。繰り返しになりますが、1制御のNANDは常に0を出力し、0制御のNANDはNOTゲートとして動作することに注意してください。S入力とR入力が両方ともハイの場合、フィードバックによってQ出力は前の状態に維持されます。どちらか一方が0の場合、出力ビットは0に固定され、もう一方はその補数に適応します。S = R =0のとき、無効状態が生成されます。

SRラッチ操作 S R アクション 0 0 Q = 1、Q = 1; 許可されません 0 1 Q = 1 1 0 Q = 0 1 1 変更なし; ランダム初期

SR NANDラッチのシンボル

SR AND-ORラッチ

SR AND-ORラッチ。薄緑は論理「1」、濃緑は論理「0」を表します。ラッチは現在ホールドモード（変化なし）です。

教育的な観点から見ると、クロスカップルされた部品（トランジスタ、ゲート、真空管など）のペアとして描かれたSRラッチは、初心者にとって理解しにくいことがよくあります。より分かりやすい説明としては、クロスカップルではなく、ラッチを単一のフィードバックループとして描くことが挙げられます。以下は、反転入力を持つANDゲートとORゲートで構成されたSRラッチです。反転入力はラッチの機能に必要ではなく、両方の入力をハイアクティブにするために必要なことに注意してください。

SR AND-ORラッチ操作

S	R	アクション
0	0	変更なし; ランダム初期
1	0	Q = 1
X	1	Q = 0

SR AND-ORラッチには、S = 1、R = 1が明確に定義されているという利点があります。上記のSR AND-ORラッチでは、R信号がS信号よりも優先されます。SをRよりも優先する必要がある場合は、出力QをANDゲートの出力ではなくORゲートの出力に接続することで実現できます。

SR AND-ORラッチは、両方のゲートを個別に説明できるため、理解しやすいです。これは、前述のANDとORの制御観点と同じです。SとRのどちらもセットされていない場合、ORゲートとANDゲートの両方が「ホールドモード」になります。つまり、入力を通過させ、出力はフィードバックループからの入力です。入力S = 1の場合、ORゲートはフィードバックループからのもう一方の入力に関係なく1を出力します（「セットモード」）。入力R = 1の場合、ANDゲートはフィードバックループからのもう一方の入力に関係なく0を出力します（「リセットモード」）。ANDゲートはORゲートの出力を入力とするため、RはSよりも優先されます。クロスカップルドゲートとして描かれたラッチは、一方のゲートの動作がもう一方のゲートと絡み合っているように見えるため、直感的に分かりにくい場合があります。標準的なNORラッチまたはNANDラッチもフィードバックループを使って再描画できますが、この場合、フィードバックループはフィードバックループ全体を通して同じ信号値を示しません。ただし、SR AND-OR ラッチには、反転した Q 出力が必要な場合に追加のインバータが必要になるという欠点があります。

SR AND-OR ラッチは、論理変換を使用して SR NOR ラッチに変換できることに注意してください。OR ゲートの出力と AND ゲートの 2 番目の入力を反転し、反転した Q 出力をこれら 2 つの追加インバータ間に接続します。ド・モルガンの法則によれば、両方の入力が反転された AND ゲートは NOR ゲートと同等になります。

JKラッチ

JKラッチはJKフリップフロップに比べて使用頻度ははるかに低いです。JKラッチは以下の状態表に従います。

JKラッチ真理値表

J	K	Q次へ	コメント
0	0	質問	変更なし
0	1	0	リセット
1	0	1	セット
1	1	質問	トグル

したがって、JKラッチは、11の入力の組み合わせが渡されると出力をトグルする（0と1の間で振動する）ように作られたSRラッチです。 ^{[ 17 ]} SRフリップフロップとは異なり、JKラッチの11の入力の組み合わせは、トグルを指示するクロックがないため、あまり役に立ちません。^{[ 18 ]}

ゲートラッチと条件付き透明性

ラッチは透過的に設計されています。つまり、入力信号の変化は出力を即座に変化させます。透過ラッチにロジックを追加することで、別の入力（「イネーブル」入力）がアサートされていないときに非透過、つまり不透明にすることができます。複数の透過ラッチが連続する場合、それらがすべて同時に透過的であれば、信号はそれらすべてを通過します。しかし、透過ハイラッチの後に透過ローラッチが続く場合（またはその逆）、状態と出力はクロックエッジでのみ変化し、いわゆるマスタースレーブフリップフロップを形成します。

ゲート式SRラッチ

NANDゲートSRラッチ。反転入力に注意してください。

ANDゲート（左）とNORゲート（右）から構成されたゲートSRラッチ回路図

ゲート付きSRラッチは、反転SRラッチに2段目のNANDゲートを追加することで作成できます。追加のNANDゲートは入力をさらに反転するため、SRラッチはゲート付きSRラッチになります（SRラッチは反転イネーブルを持つゲート付きSRラッチに変換されます）。

あるいは、SR ラッチに第 2 レベルの AND ゲートを追加することで、ゲート付き SR ラッチ(非反転イネーブル付き) を作成することもできます。

E がハイ（有効が真）の場合、信号は入力ゲートを通過してカプセル化されたラッチに渡されます。(0, 0) =ホールドを除くすべての信号の組み合わせは、(Q, Q ) 出力で直ちに再現されます。つまり、ラッチは透過的です。

E が低い場合 ( enable がfalse)、ラッチは閉じられ (不透明)、E が最後に高かったときの状態のままになります。

周期的なイネーブル入力信号は、ライトストローブと呼ばれることもあります。イネーブル入力がクロック信号である場合、ラッチはレベルセンシティブ（クロック信号のレベルに対して）であると言われます。これは、後述するフリップフロップのような エッジセンシティブとは対照的です。

ゲートSRラッチ操作 電気通信 アクション 0 アクションなし（保留状態） 1 非ゲートSRラッチと同じ

ゲートSRラッチのシンボル

ゲート式Dラッチ

このラッチは、ゲーテッドSRラッチの2つのアクティブな入力の組み合わせ（01と10）において、RがSの補数であるという事実を利用しています。入力NAND段は、データ入力信号を反転することにより、2つのD入力状態（0と1）を次のSRラッチのこれらの2つの入力組み合わせに変換します。イネーブル信号がロー状態の場合、非アクティブな「11」の組み合わせが生成されます。したがって、ゲーテッドDラッチは、1入力同期SRラッチと考えることができます。この構成により、制限された入力組み合わせの適用が防止されます。これは、トランスペアレントラッチ、データラッチ、または単にゲーテッドラッチとも呼ばれます。データ入力とイネーブル信号（クロックまたは制御と呼ばれることもあります）を備えています。 「トランスペアレント」という言葉は、イネーブル入力がオンの場合、信号が回路を介して入力Dから出力Qに直接伝播するという事実に由来しています。ゲーテッドDラッチは、クロックまたはイネーブル信号のレベルに対して レベルセンシティブでもあります。

透過ラッチは、通常、I/O ポートとして、または非同期システム、または同期 2 相システム ( 2 相クロックを使用する同期システム) で使用されます。同期 2 相システムでは、異なるクロック位相で動作する 2 つのラッチが、マスター スレーブ フリップフロップのようにデータの透過性を防ぎます。

下の真理値表は、イネーブル/クロック入力が0の場合、D入力は出力に影響を与えないことを示しています。E / Cがハイの場合、出力はDに等しくなります。

ゲートDラッチ真理値表 電気通信 D 質問 質問 コメント 0 X Q前 Q前 変更なし 1 0 0 1 リセット 1 1 1 0 セット

ゲート付きDラッチのシンボル

• 
  SR NANDラッチに基づくゲートDラッチ
• 
  SR NORラッチに基づくゲートDラッチ
• 
  アニメーション化されたゲート式Dラッチ。黒と白はそれぞれ論理「1」と「0」を意味します。

  1. D = 1、E = 1: セット
  2. D = 1、E = 0: ホールド
  3. D = 0、E = 0: ホールド
  4. D = 0、E = 1: リセット
• 
  パストランジスタロジックのゲートDラッチ。CD4042やCD74HC75集積回路に使用されているものと同様。

アールラッチ

古典的なゲートラッチ設計には、いくつか望ましくない特性があります。^{[ 19 ]}これらの設計では、デュアルレールロジックまたはインバータが必要です。入力から出力への伝播には最大3ゲート遅延かかる場合があります。また、入力から出力への伝播は一定ではなく、出力によっては2ゲート遅延かかるものもあれば、3ゲート遅延かかるものもあります。

設計者たちは代替手段を探した。^{[ 20 ]}成功した代替手段はアールラッチである。これは単一のデータ入力のみを必要とし、その出力には一定の2ゲート遅延がかかる。さらに、アールラッチの2つのゲートレベルは、場合によってはラッチを駆動する回路の最後の2つのゲートレベルとマージすることができる。これは、多くの一般的な計算回路が最後の2つのレベルとしてOR層とAND層を持っているためである。ラッチ機能をマージすることで、追加のゲート遅延なしでラッチを実装することができる。^{[ 19 ]}このマージはパイプライン型コンピュータの設計でよく利用されており、実際、もともとジョン・G・アールによってIBM System/360 Model 91でその目的で使用するために開発されたものである。^{[ 21 ]}

アールラッチはハザードフリーである。^{[ 22 ]}中間のNANDゲートを省略すると、論理演算量が少なくて済むため一般的に用いられる極性保持ラッチとなる。 ^{[ 22 ] [ 23 ]}しかし、これは論理ハザードの影響を受けやすい。クロック信号を意図的にスキューさせることで、このハザードを回避できる。^{[ 23 ]}

• 
  Earleラッチは相補的なイネーブル入力を使用します: イネーブルアクティブロー(E_L)とイネーブルアクティブハイ(E_H)
• 
  アニメーション化されたアールラッチ。黒と白はそれぞれ論理「1」と「0」を意味します。

  1. D = 1、E_H = 1: 設定
  2. D = 0、E_H = 1: リセット
  3. D = 1、E_H = 0: ホールド

Dフリップフロップ

Dフリップフロップシンボル

Dフリップフロップは広く用いられており、「データ」フリップフロップとして知られています。Dフリップフロップは、クロックサイクルの特定の部分（例えばクロックの立ち上がりエッジ）でD入力の値をキャプチャします。キャプチャされた値はQ出力となります。それ以外の時間では、出力Qは変化しません。^{[ 24 ] [ 25 ]} Dフリップフロップは、メモリセル、ゼロ次ホールド、または遅延線として見ることができます。^{[ 26 ]}

真理値表:

クロック	D	Q次へ
上昇エッジ	0	0
上昇エッジ	1	1
上昇しない	X	質問

（Xはdon't care条件を示し、信号が無関係であることを意味します）

IC内のほとんどのD型フリップフロップは、SRフリップフロップと同様に、セット状態またはリセット状態（D入力とクロック入力を無視）に強制的に設定できます。通常、S = R = 1という不正な状態はD型フリップフロップで解決されます。S = R = 0に設定すると、フリップフロップは上記のように動作します。その他のSおよびR設定の真理値表を以下に示します。

入力				出力
S	R	D	>	質問	質問
0	1	X	X	0	1
1	0	X	X	1	0
1	1	X	X	1	1

4ビットシリアル入力パラレル出力（SIPO）シフトレジスタ

これらのフリップフロップは、多くの電子機器に不可欠な要素であるシフトレジスタの基礎となるため、非常に有用です。DフリップフロップがD型「トランスペアレントラッチ」よりも優れている点は、D入力ピンの信号がフリップフロップにクロックが供給された瞬間にキャプチャされ、その後のD入力の変化は次のクロックイベントまで無視されることです。例外として、一部のフリップフロップには「リセット」信号入力があり、Qをリセット（ゼロに）します。このリセット信号はクロックと非同期または同期のいずれかになります。

上記の回路は、クロックのアクティブ遷移ごとにレジスタの内容を1ビット右にシフトします。入力Xは最左端のビット位置にシフトされます。

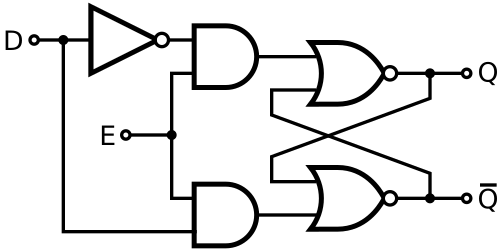
古典的なポジティブエッジトリガーDフリップフロップ

エッジトリガーDフリップフロップのいくつかの異なるタイプ

ポジティブエッジトリガーDフリップフロップ

セットとリセットを備えたポジティブエッジトリガーDフリップフロップ

この回路^{[ 27 ]}は、 SR NAND ラッチによって実装された 2 つのステージで構成されています。入力ステージ (左側の 2 つのラッチ) は、クロック信号とデータ信号を処理して、出力ステージ (右側の 1 つのラッチ) への正しい入力信号を確保します。クロックがローの場合、データ入力に関係なく、入力ステージの両方の出力信号がハイになります。出力ラッチは影響を受けず、前の状態を保存します。クロック信号がローからハイに変化すると、出力電圧の 1 つだけ (データ信号に依存) がローになり、出力ラッチをセット/リセットします。D = 0 の場合、下側の出力がローになり、D = 1 の場合、上の出力がローになります。クロック信号がハイのままである限り、これらの入力ステージ出力はデータ入力に関係なくその状態を維持し、出力ラッチを対応する状態に維持します。これは、クロックがハイの間、(出力ステージの) 入力論理 0 がアクティブのままであるためです。クロックがハイの間にデータ入力が変化しても、2 つの入力ステージラッチの状態は変化しません。したがって、出力ラッチの役割は、クロックが低い間のみデータを保存することです。

この回路はゲーテッドDラッチと密接な関連があり、どちらの回路もデータ入力信号を反転することで、2つのD入力状態（0と1）を出力SRラッチの2つの入力組み合わせ（01と10）に変換します（どちらの回路も単一のD信号を2つの相補的なS信号とR信号に分割します）。違いは、ゲーテッドDラッチではNAND論理ゲートが使用されるのに対し、ポジティブエッジトリガDフリップフロップではSR NANDラッチが使用されることです。これらのラッチの役割は、アクティブ出力を「ロック」して低電圧（論理ゼロ）を生成することです。したがって、ポジティブエッジトリガDフリップフロップは、ラッチ入力ゲートを備えたゲーテッドDラッチと考えることもできます。

マスタースレーブエッジトリガーDフリップフロップ

マスタースレーブ型のDフリップフロップ。イネーブル入力（通常はクロック）の立ち下がりエッジで応答します。

クロックの立ち上がりエッジでトリガーされるマスタースレーブDフリップフロップの実装

マスタースレーブ型Dフリップフロップは、2つのゲート付きDラッチを直列に接続し、一方のイネーブル入力を反転することで構成されます。マスターラッチがスレーブラッチの出力値Qを制御し、スレーブラッチがイネーブルされている間は常にスレーブラッチにその値を保持させるため、マスタースレーブと呼ばれます。スレーブラッチは常にマスターラッチから新しい値をコピーし、マスターラッチの値とクロック信号の変化に応じてのみ値を変更します。

ポジティブエッジトリガのマスター・スレーブDフリップフロップでは、クロック信号がロー（論理0）のとき、最初のDラッチ（マスターラッチ）の「イネーブル」（反転クロック信号）はハイ（論理1）になります。これにより、「マスター」ラッチはクロック信号がローからハイに遷移した際に入力値を保存できます。クロック信号がハイ（0から1）に遷移すると、最初のラッチの反転された「イネーブル」がロー（1から0）になり、マスターラッチへの入力値が「ロック」されます。ほぼ同時に、2番目のDラッチ（スレーブラッチ）の2回反転された「イネーブル」がクロック信号とともにローからハイ（0から1）に遷移します。これにより、クロックの立ち上がりエッジで「ロック」されたマスターラッチによってキャプチャされた信号が、「スレーブ」ラッチを通過できるようになります。クロック信号がロー（1 から 0）に戻ると、「スレーブ」ラッチの出力は「ロック」され、クロックの最後の立ち上がりエッジで確認された値が保持され、「マスター」ラッチは次の立ち上がりクロックエッジに備えて新しい値の受け入れを開始します。

回路の左端のインバータを取り除くと、クロック信号の 立ち下がりエッジでストローブするD型フリップフロップが作成されます。この真理値表は次のようになります。

D	質問	>	Q次へ
0	X	落下	0
1	X	落下	1

デュアルエッジトリガーDフリップフロップ

デュアルエッジトリガーDフリップフロップの実装

クロックの立ち上がりエッジと立ち下がりエッジで新しい値を読み取るフリップフロップは、デュアルエッジトリガ型フリップフロップと呼ばれます。このようなフリップフロップは、2つのシングルエッジトリガ型D型フリップフロップとマルチプレクサ、または2つのシングルエッジトリガ型D型フリップフロップと3つのXORゲートを使用して構築できます。

デュアルエッジトリガーDフリップフロップの回路記号

XORゲートを使用して実装されたデュアルエッジトリガーDフリップフロップ。マルチプレクサは使用しない。

エッジトリガーダイナミックDストレージ要素

リセット機能付きダイナミックエッジトリガーフリップフロップのCMOS IC実装

Dフリップフロップの効率的な機能的代替として、十分な頻度でクロックを供給できるダイナミック回路（情報を容量に記憶する回路）が考えられます。真のフリップフロップではありませんが、機能上はフリップフロップと呼ばれます。マスター・スレーブ型のDフリップフロップはクロックのエッジでトリガーされますが、各コンポーネントはクロックレベルによってトリガーされます。真のフリップフロップではないにもかかわらず「エッジトリガー型Dフリップフロップ」と呼ばれるこの回路は、マスター・スレーブの特性を備えていません。

エッジトリガーDフリップフロップは、ダイナミックロジックを用いた高速動作の統合システムでよく使用されます。これは、デバイスが遷移していない間、デジタル出力がデバイスの寄生容量に保存されることを意味します。この設計により、1つまたは複数の内部ノードを放電するだけでリセットが可能になります。一般的なダイナミックフリップフロップの種類は、真のシングルフェーズクロック（TSPC）型で、フリップフロップの動作を低消費電力かつ高速に実行します。ただし、ダイナミックフリップフロップは通常、静的または低クロック速度では動作しません。十分な時間があれば、リークパスによって寄生容量が十分に放電され、フリップフロップが無効な状態になる可能性があるためです。

Tフリップフロップ

T型フリップフロップの回路記号

T入力がハイの場合、Tフリップフロップはクロック入力がストローブされるたびに状態を変化（「トグル」）させます。T入力がローの場合、フリップフロップは前の値を保持します。この動作は特性方程式で記述されます。

${\displaystyle Q_{\text{next}}=T\oplus Q=T{\overline {Q}}+{\overline {T}}Q}$ （XOR演算子の展開）

これは真理値表で表すことができます。

Tフリップフロップ動作^{[ 28 ]}

特性表				励起テーブル
${\displaystyle T}$	${\displaystyle Q}$	${\displaystyle Q_{\text{next}}}$	コメント	${\displaystyle Q}$	${\displaystyle Q_{\text{next}}}$	${\displaystyle T}$	コメント
0	0	0	ホールド状態（クロックなし）	0	0	0	変更なし
0	1	1	ホールド状態（クロックなし）	1	1	0	変更なし
1	0	1	トグル	0	1	1	補体
1	1	0	トグル	1	0	1	補体

Tがハイに保持されると、トグル・フリップフロップはクロック周波数を2分周します。つまり、クロック周波数が4MHzの場合、フリップフロップから得られる出力周波数は2MHzになります。この「分周」機能は、様々なタイプのデジタルカウンタに応用されています。Tフリップフロップは、JKフリップフロップ（JピンとKピンが接続され、Tピンとして機能します）またはDフリップフロップ（T入力とQピンのXORがD入力を駆動します） _{を使用して構築することもできます。}

JKフリップフロップ

ポジティブエッジトリガーJKフリップフロップの回路記号

JKフリップフロップのタイミング図

JKフリップフロップは、J = K = 1 の状態を「フリップ」またはトグルコマンドとして解釈することで、SRフリップフロップ（J：セット、K：リセット）の動作を拡張します。具体的には、J = 1、K = 0 の組み合わせはフリップフロップをセットするコマンド、J = 0、K = 1 の組み合わせはフリップフロップをリセットするコマンド、J = K = 1 の組み合わせはフリップフロップをトグルするコマンド、つまり出力を現在の値の論理補数に変更するコマンドです。J = K = 0 に設定すると、現在の状態が維持されます。Dフリップフロップを合成するには、KをJの補数に設定するだけです（入力Jは入力Dとして機能します）。同様に、Tフリップフロップを合成するには、KをJに設定します。したがって、JKフリップフロップは、SRフリップフロップ、Dフリップフロップ、またはTフリップフロップとして動作するように構成できるため、汎用フリップフロップです。

JK フリップフロップの特性方程式は次のとおりです。

${\displaystyle Q_{\text{next}}=J{\overline {Q}}+{\overline {K}}Q}$

対応する真理表は次のようになります。

JKフリップフロップ演算^{[ 28 ]}

特性表				励起テーブル
J	K	コメント	Q次へ	質問	Q次へ	コメント	J	K
0	0	保留状態	質問	0	0	変更なし	0	X
0	1	リセット	0	0	1	セット	1	X
1	0	セット	1	1	0	リセット	X	1
1	1	トグル	質問	1	1	変更なし	X	0

タイミングの考慮

タイミングパラメータ

フリップフロップのセットアップ、ホールド、クロックから出力までのタイミングパラメータ

入力は、クロックの立ち上がりエッジ周辺の、アパーチャと呼ばれる期間、一定に保たれなければなりません。スイレンの葉の上でカエルの写真を撮ることを想像してください。^{[ 29 ]}カエルが水に飛び込むとします。カエルが水に飛び込む瞬間を写真に撮ると、カエルが水に飛び込むところがぼやけて写り、カエルがどの状態にあったかは分かりません。しかし、カエルがパッドの上に安定して座っている（または水の中に安定している）間に写真を撮れば、鮮明な画像が得られます。同様に、フリップフロップへの入力は、フリップフロップの アパーチャ期間中、一定に保たれなければなりません。

セットアップ時間とは、クロックによってデータが確実にサンプリングされるように、クロック イベント の前にデータ入力を一定に保持する必要がある最小時間です。

ホールド時間とは、クロックによってデータが確実にサンプリングされるように、クロック イベント 後にデータ入力が一定に保持される最小時間です。

アパーチャはセットアップ時間とホールド時間の合計です。この時間中、データ入力は一定に保たれなければなりません。^{[ 29 ]}

回復時間とは、クロックイベントの前に非同期セット入力またはリセット入力が非アクティブになっていなければならない最小時間であり、これによりデータがクロックによって確実にサンプリングされます。したがって、非同期セット入力またはリセット入力の回復時間は、データ入力のセットアップ時間とほぼ同じです。

リムーバルタイムとは、クロックイベント後に非同期セット入力またはリセット入力が非アクティブになっていなければならない最小時間であり、これによりデータがクロックによって確実にサンプリングされます。したがって、非同期セット入力またはリセット入力のリムーバルタイムは、データ入力のホールドタイムとほぼ同じです。

非同期入力（セット、リセット）に印加さ​​れる短いインパルスは、回復時間から除去時間までの期間内に完全に印加すべきではありません。そうしないと、フリップフロップが適切な状態に遷移するかどうかが全く予測できなくなります。また、非同期信号が回復時間から除去時間の間に一度だけ遷移した場合、フリップフロップは最終的に適切な状態に遷移しますが、同期入力信号に応じて、出力に非常に短いグリッチが発生する場合と発生しない場合があります。この後者の状況は、回路設計において重要な意味を持つ場合とそうでない場合があります。

セット信号とリセット信号 (およびその他の信号) は同期または非同期のいずれかであるため、セットアップ/ホールド時間または回復/削除時間のいずれかで特徴付けられ、同期性はフリップフロップの設計に大きく依存します。

大規模回路のタイミング検証では、非同期信号が同期信号よりも重要度が低い場合が多いため、セットアップ/ホールド時間とリカバリ/リムーバル時間を区別することがしばしば必要になります。この区別により、回路設計者はこれらの信号タイプごとに検証条件を個別に定義できるようになります。

準安定性

フリップフロップはメタスタビリティと呼ばれる問題を抱えている。これは、データとクロック、あるいはクロックとリセットといっ​​た2つの入力がほぼ同時に変化した場合に発生する可能性がある。適切なタイミング制約内で順序が明確でない場合、出力は予測不能な動作をし、いずれかの状態に落ち着くまでに通常よりも何倍も時間がかかったり、落ち着くまでに何度も振動したりすることさえある。理論上、落ち着くまでの時間は有限ではない。コンピュータシステムでは、このメタスタビリティによって、別の回路がその値を使用する前に状態が安定していない場合に、データの破損やプログラムのクラッシュが発生する可能性がある。特に、2つの異なる論理パスがフリップフロップの出力を使用する場合、一方のパスはそれを安定状態に解決していないにもかかわらず0と解釈し、もう一方のパスは1と解釈し、マシンを不整合な状態に陥らせる可能性がある。^{[ 30 ]}

フリップフロップのメタスタビリティは、クロックパルスの前後にそれぞれセットアップ時間（t _su）とホールド時間（t _h）と呼ばれる一定時間、データ入力と制御入力が有効かつ一定に保たれるようにすることで回避できます。これらの時間はデバイスのデータシートに記載されており、最新のデバイスでは通常、数ナノ秒から数百ピコ秒の範囲です。フリップフロップの内部構成によっては、セットアップ時間またはホールド時間をゼロ（あるいは負）に抑えたデバイスを構築できますが、両方を同時に満たすことはできません。

残念ながら、セットアップとホールドの基準を常に満たすことができるとは限りません。なぜなら、フリップフロップは設計者の制御外でいつでも変化する可能性のあるリアルタイム信号に接続される場合があるからです。この場合、設計者にできる最善の策は、回路に求められる信頼性に応じて、エラーの確率を一定のレベルまで低減することです。メタスタビリティを抑制する一つの手法は、2つ以上のフリップフロップをチェーン接続し、各フリップフロップの出力を次のフリップフロップのデータ入力に供給し、すべてのデバイスで共通のクロックを共有することです。この方法により、メタスタビリティの発生確率を無視できるレベルまで低減できますが、ゼロにすることはできません。直列接続されたフリップフロップの数が増えるにつれて、メタスタビリティの発生確率はゼロに近づきます。カスケード接続されるフリップフロップの数は「ランク付け」と呼ばれ、「デュアルランク」フリップフロップ（2つのフリップフロップを直列に接続）は一般的な状況です。

いわゆるメタステーブル耐性強化フリップフロップは、セットアップ時間とホールド時間を可能な限り短縮することで機能しますが、それでも問題を完全に排除することはできません。これは、メタステーブルが単なる回路設計の問題ではないためです。クロックとデータの遷移が時間的に近い場合、フリップフロップはどちらのイベントが最初に発生したかを判断しなければなりません。デバイスがどれだけ高速に製造されたとしても、入力イベントが非常に近いため、どちらが最初に発生したかを検出できない可能性が常にあります。したがって、完全にメタステーブル耐性のあるフリップフロップを構築することは論理的に不可能です。フリップフロップは、最大セトリング時間（特定の条件下でメタステーブル状態を維持できる最大時間）で特性評価されることがあります。この場合、最大許容メタステーブル時間よりも遅いクロックで動作するデュアルランクのフリップフロップは、非同期（外部など）信号に対して適切な調整を提供します。

伝播遅延

フリップフロップのもう一つの重要なタイミング値は、クロック出力遅延（データシートでよく使われる記号：t _CO）または伝播遅延（t _P）です。これは、クロックエッジからフリップフロップの出力が変化するまでの時間です。ハイからローへの遷移時間（t _{PHL ）は、ローからハイへの遷移時間（t PLH} ）と異なる場合があります。

シフトレジスタのように、同じクロックを共有するフリップフロップをカスケード接続する場合、先行するフリップフロップのt _{COが後続のフリップフロップのホールド時間（t h}）よりも長く、後続のフリップフロップの入力データがクロックのアクティブエッジに続いて適切に「シフトイン」されるようにすることが重要です。t COとt _{hの関係は、フリップフロップが物理的に同一であれば通常保証されます。さらに、正しく動作させるためには、クロック周期がt su}  + t _hの合計よりも大きくなければならないことは容易に確認できます。

一般化

フリップフロップは、少なくとも2つの方法で一般化できます。1-of-2ではなく1-of-Nにすること、そして2つ以上の状態を持つ論理に適応させることです。1-of-3エンコーディング、または多値3値論理などの特殊なケースでは、このような要素はフリップフラップフロップと呼ばれることがあります。^{[ 31 ]}

従来のフリップフロップでは、2つの相補出力のうち正確に1つだけがハイになります。これは、N個の出力を持ち、そのうち正確に1つだけがハイになる（あるいは、N個のうち正確に1つがローになる）メモリ素子に一般化できます。したがって、出力は常に1ホット（または1コールド）表現となります。構造は従来のクロスカップルドフリップフロップに似ており、各出力がハイになると、他のすべての出力が抑制されます。^{[ 32 ]}あるいは、出力ごとに1つのフリップフロップを使用し、一度に1つだけが真になるように追加回路を追加することで、従来型のフリップフロップを複数使用することもできます。^{[ 33 ]}

従来のフリップフロップのもう一つの一般化は、多値論理のためのメモリ素子である。この場合、メモリ素子は制御入力によって変化が誘発されるまで、論理状態のうちの1つだけを保持する。^{[ 34 ]}さらに、多値クロックも使用でき、新たなクロック遷移が可能となる。^{[ 35 ]}

注記

1. あるいは、2つの入力をそれぞれセット1とセット0と呼ぶこともできます。これにより、一部の混乱を避けることができます。「セット」という用語だけでは、セットする入力にビットを設定すると誤解される可能性があります。また、この命名により、以下の説明で、0と1を同時にセットしようとするとSRラッチが予期せぬ動作をすることが直感的に理解しやすくなります。

参照

• ラッチングリレー
• 低消費電力フリップフロップ
• パルス遷移検出器
• サンプルアンドホールド
• シュミットトリガー
• 静的ランダムアクセスメモリ

参考文献

1. 例えば、 Digital Equipment Corporationの Logic Handbook Flip Chip™ Modules 1969 版では、透過型 RS ラッチを「R/S フリップフロップ」と呼んでいます ( http://www.bitsavers.org/pdf/dec/handbooks/Digital_Logic_Handbook_1969.pdf 44 ページ)
2. Digital Equipment Corporation の Logic Handbook Flip Chip™ Modules 1969 版の別の例として、真理値表とともに「R/S フリップフロップ」と「クロック付き」の「R/S フリップフロップ」について説明されています。( http://www.bitsavers.org/pdf/dec/handbooks/Digital_Logic_Handbook_1969.pdf 8 ページ)
3. Pedroni, Volnei A. (2008). VHDLによるデジタルエレクトロニクスと設計. Morgan Kaufmann. p. 329. ISBN 978-0-12-374270-4。
4. ラッチとフリップフロップArchived 2016-10-05 at the Wayback Machine (EE 42/100 Lecture 24 from Berkeley) 「フリップフロップとラッチという用語は互換的に使用されることがあります...」
5. ロス, チャールズ H. ジュニア (1995). 「ラッチとフリップフロップ」.ロジック設計の基礎(第4版). PWS. ISBN 9780534954727。
6. GB 148582、エクルズ、ウィリアム・ヘンリー、ジョーダン、フランク・ウィルフレッド、「イオンリレーの改良」、1920年8月5日発行 
7. 参照:
   • エクルズ, WH; ジョーダン, FW (1919年9月19日). 「三電極熱電子真空管を用いたトリガーリレー」 . 『The Electrician』 , 83 : 298.
   • 転載： エクルズ, WH; ジョーダン, FW (1919年12月). 「3電極熱電子真空管を用いたトリガーリレー」 . 『ラジオ・レビュー』 . 1 (3): 143–6 .
   • エクルズ, WH; ジョーダン, FW (1919). 「3電極熱電子真空管を用いたトリガーリレー」英国科学振興協会第87回会議報告書: ボーンマス: 1919年9月9日～13日. pp.  271 ～ 22.の要約。
8. Pugh, Emerson W.; Johnson, Lyle R.; Palmer, John H. (1991). IBM 360および初期の370システム. MIT Press. p.  10. ISBN 978-0-262-16123-7。
9. Flowers, Thomas H. (1983), "The Design of Colossus" , Annals of the History of Computing , 5 (3): 249, doi : 10.1109/MAHC.1983.10079 , S2CID 39816473 , 2006年3月26日アーカイブ, 2015年6月16日取得 
10. ゲイツ、アール・D. (2000).エレクトロニクス入門（第4版）. デルマー・トムソン（Cengage）ラーニング. p. 299. ISBN 978-0-7668-1698-5。
11. Fogiel, Max; Gu, You-Liang (1998). 『エレクトロニクス問題解決ツール』第1巻（改訂版）. Research & Education Assoc. p. 1223. ISBN 978-0-87891-543-9。
12. Lindley, PL (1968年8月). 「1968年6月13日付の手紙」. EDN .
13. フィスター、モンゴメリー (1958). 『デジタルコンピュータの論理設計』 ワイリー社. p. 128. ISBN 9780608102658。
14. US 2850566、ネルソン、エルドレッド C.、「高速印刷システム」、1958 年 9 月 2 日公開、ヒューズ エアクラフト社に譲渡。 
15. Langholz, Gideon; Kandel, Abraham; Mott, Joe L. (1998). 『デジタルロジック設計の基礎』ワールドサイエンティフィック社 p. 344. ISBN 978-981-02-3110-1。
16. 「フリップフロップ行動の種類のまとめ」Wayback Machineで2018年4月19日にアーカイブ。2018年4月16日閲覧。
17. Hinrichsen, Diederich; Pritchard, Anthony J. (2006). 「例1.5.6 (R–SラッチとJ–Kラッチ)」 .数理システム理論I：モデリング、状態空間解析、安定性、ロバスト性. Springer. pp.  63– 64. ISBN 9783540264101。
18. ファーハット、ハッサン A. (2004).デジタルデザインとコンピュータ組織. 第1巻. CRC Press. p. 274. ISBN 978-0-8493-1191-8。
19. コッゲ、ピーター・M. (1981).パイプラインコンピュータのアーキテクチャ. マグロウヒル. pp.  25– 27. ISBN 0-07-035237-2。
20. Cotten, LW (1965). 「高速パイプラインシステムの回路実装」. 1965年11月30日～12月1日開催の秋季合同コンピュータ会議議事録、第1部 XX - AFIPS '65 (秋季、第1部) . pp.  489– 504. doi : 10.1145/1463891.1463945 . S2CID 15955626 . 
21. Earle, John G. (1965年3月). 「ラッチ式キャリーセーブ加算器」. IBM技術情報開示速報. 7 (10): 909–910 .
22. オモンディ、アモス・R. (1999).パイプライン型およびスーパースカラ型コンピュータのマイクロアーキテクチャ. シュプリンガー. pp.  40– 42. ISBN 978-0-7923-8463-2。
23. Kunkel, Steven R.; Smith, James E. (1986年5月). 「スーパーコンピュータにおける最適パイプライン」. ACM SIGARCH Computer Architecture News . 14 (2). ACM: 404–411 [406]. CiteSeerX 10.1.1.99.2773 . doi : 10.1145/17356.17403 . ISSN 0163-5964 . S2CID 2733845 .   
24. 「Dフリップフロップ」 2014年2月23日時点のオリジナルよりアーカイブ。2016年6月5日閲覧。
25. 「エッジトリガー・フリップフロップ」 。 2013年9月8日時点のオリジナルよりアーカイブ。2011年12月15日閲覧。
26. Eckert, J. (1953). 「デジタルコンピュータメモリシステムの概観」. Proceedings of the IRE . 41 (10): 1393–1406 . doi : 10.1109/JRPROC.1953.274316 .
27. SN7474 TI データシート
28. マノ, M. モリス; キム, チャールズ R. (2004). 『ロジックとコンピュータ設計の基礎』第3版. アッパーサドルリバー, ニュージャージー州, 米国: ピアソン・エデュケーション・インターナショナル. p. 283. ISBN 0-13-191165-1。
29. Harris, S; Harris, D (2016).デジタル設計とコンピュータアーキテクチャ - ARM版. Morgan Kaufmann, Waltham, MA. ISBN 978-0-12-800056-4。
30. Chaney, Thomas J.; Molnar, Charles E. (1973年4月). 「同期回路とアービタ回路の異常な動作」. IEEE Transactions on Computers . C-22 (4): 421– 422. doi : 10.1109/TC.1973.223730 . ISSN 0018-9340 . S2CID 12594672 .  
31. Don Knuth ( 1969)の著作とされることが多い（ Midhat J. Gazalé (2000) を参照）。番号: Ahmes から Cantor まで。プリンストン大学出版局。p. 57。ISBN 978-0-691-00515-7。（注：原文に「フリップフラップフロップ」という語句が出てくるのは、実際にはコンピューティング文献においてかなり以前から存在していた。例えば、 Bowdon, Edward K. (1960) など。トンネルダイオードを用いた「フリップフラップフロップ」の設計と応用（修士論文）。ノースダコタ大学。および Alexander, W. (1964年2月). 「三進法コンピュータ」 . Electronics and Power . 10 (2). IET: 36– 39. doi : 10.1049/ep.1964.0037 .
32. 「三進法の「フリップフラップフロップ」. 2009年1月5日時点のオリジナルよりアーカイブ。2009年10月17日閲覧。
33. US 6975152、Lapidus、Peter D.、「ワンホットバス上でグリッチレス操作をサポートするフリップフロップおよびその方法」、2005年12月13日公開、Advanced Micro Devices Inc.に譲渡。 
34. Irving, Thurman A.; Shiva, Sajjan G.; Nagle, H. Troy (1976年3月). 「多値ロジックのためのフリップフロップ」. IEEE Transactions on Computers . C-25 (3): 237– 246. doi : 10.1109/TC.1976.5009250 . S2CID 34323423 . 
35. Wu, Haomin; Zhuang Nan (1991年7月). 「三値エッジトリガーJKLフリップフロップの研究」. Journal of Electronics (China) . 8 (3): 268– 275. doi : 10.1007/BF02778378 . S2CID 61275953 . 

外部リンク

• FlipFlop Hierarchy Archived 2015-04-08 at the Wayback Machineは、インタラクティブなフリップフロップ回路を示しています。
• JKフリップフロップ
• デジタルエレクトロニクスにおけるフリップフロップ
• シャリフ、ケン（2022年8月）「X線CTスキャンを用いた1960年代のハイブリッド・フリップフロップ・モジュールのリバースエンジニアリング」