斜め格子

抽象代数学において、歪格子（ひずみ格子）は、格子の非可換な一般化である代数構造である。歪格子という用語は、格子の非可換な一般化全般を指すために用いられるが、1989年以降、主に以下の意味で用いられている。

意味

歪んだ格子とは、 meetとjoinと呼ばれる結合的でべき等な2項演算とを備えた集合Sであり、次の吸収法則の双対を検証する。 ${\displaystyle \wedge}$ ${\displaystyle \vee}$

${\displaystyle x\wedge (x\vee y)=x=(y\vee x)\wedge x}$ 、

${\displaystyle x\vee (x\wedge y)=x=(y\wedge x)\vee x}$ 。

および は結合性とべき等性を持つため、これらの恒等式は次のステートメントの双対を検証することと同等です。 ${\displaystyle \vee}$ ${\displaystyle \wedge}$

${\displaystyle x\vee y=x}$ の場合に限り、${\displaystyle x\wedge y=y}$

${\displaystyle x\wedge y=x}$ 場合、かつその場合に限ります。^{[ 1 ]}${\displaystyle x\vee y=y}$

歴史的背景

60年以上にわたり、格子の非可換変種は様々な動機から研究されてきた。その動機は、格子理論の概念的限界への関心であったり、論理やブール代数の非可換形式の探索であったり、環におけるべき等性の挙動であったりする。一般的に、非可換格子とは、とが結合的かつべき等な二項演算であり、吸収恒等式で結ばれており、何らかの形でが双対化することを保証する代数である。選択される正確な恒等式は根底にある動機に依存し、異なる選択によって異なる種類の代数が生じる。 ${\displaystyle (S;\wedge,\vee)}$ ${\displaystyle \wedge}$ ${\displaystyle \vee}$ ${\displaystyle \wedge}$ ${\displaystyle \vee}$

パスクアル・ジョーダンは、量子論理の疑問に触発され、 1949年の論文「Über Nichtkommutative Verbände」 [ ^{2 ]で}非可換格子の研究を開始し、吸収恒等式を選択した。

${\displaystyle x\wedge (y\vee x)=x=(x\wedge y)\vee x.}$

彼は、それらを満たす代数をSchrägverbändeと呼んだ。これらの恒等式を変形または拡張することで、ジョーダンらは様々な非可換格子を得た。ジョナサン・リーチの1989年の論文「環内の歪んだ格子」 [ ^{1 ]以来}、上で定義した歪んだ格子が主要な研究対象となってきた。これは、バンドに関する先行研究の結果によって助けられた。これは特に、多くの基本的性質に当てはまった。

基本的なプロパティ

自然半順序と自然準順序

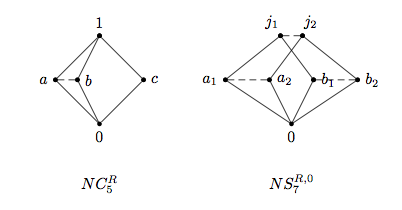
歪んだ格子 において、自然な半順序は 、あるいは双対的に 、で定義されます。の自然な前順序は 、あるいは双対的に 、で与えられます。と が格子上で一​​致する一方で、非可換な場合にはを適切に精緻化します。が、すなわち 、 あるいは双対的に 、および、で定義される自然同値性。 の分割のブロックが 格子順序付けされている場合、かつ 、となる場合のみに限ります。これにより、次のペアのような歪んだ格子のハッセ図を描くことができます。 ${\displaystyle S}$ ${\displaystyle y\leq x}$ ${\displaystyle x\wedge y=y=y\wedge x}$ ${\displaystyle x\vee y=x=y\vee x}$ ${\displaystyle S}$ ${\displaystyle y\preceq x}$ ${\displaystyle y\wedge x\wedge y=y}$ ${\displaystyle x\vee y\vee x=x}$ ${\displaystyle \leq }$ ${\displaystyle \preceq}$ ${\displaystyle \leq }$ ${\displaystyle \preceq}$ ${\displaystyle D}$ ${\displaystyle xDy}$ ${\displaystyle x\preceq y\preceq x}$ ${\displaystyle x\wedge y\wedge x=x}$ ${\displaystyle y\wedge x\wedge y=y}$ ${\displaystyle x\vee y\vee x=x}$ ${\displaystyle y\vee x\vee y=y}$ ${\displaystyle S/D}$ ${\displaystyle A>B}$ ${\displaystyle a\in A}$ ${\displaystyle b\in B}$ ${\displaystyle a>b}$

例えば、上の左側の図では、と が関連していることが破線で表現されています。斜線は、異なる-クラスの要素間の自然な半順序を示しています。要素、、 は、シングルトン-クラスを形成します。 ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle D}$ ${\displaystyle D}$ ${\displaystyle 1}$ ${\displaystyle c}$ ${\displaystyle 0}$ ${\displaystyle D}$

長方形の斜め格子

単一の -クラスからなる歪んだ格子は、長方格子と呼ばれます。これらは、等価な恒等式、 および によって特徴付けられます。長方歪んだ格子 は、次の構成を持つ歪んだ格子 と同型です (逆もまた同様です): 空でない集合 および が与えられたとき、およびを定義します。上の図で示されているように、歪んだ格子 の -クラス分割は、をその最大長方部分代数 に一意に分割したものです。さらに、はの最大格子像である誘導商代数と合同であり、したがってすべての歪んだ格子 は長方部分代数の格子になります。これは歪んだ格子 の Clifford–McLean の定理であり、Cliffordと McLean によってバンド に対して別々に初めて示されました。これは歪んだ格子 の最初の分解定理としても知られています。 ${\displaystyle D}$ ${\displaystyle x\wedge y\wedge x=x}$ ${\displaystyle y\vee x\vee y=y}$ ${\displaystyle x\vee y=y\wedge x}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle L\times R}$ ${\displaystyle (x,y)\vee (z,w)=(z,y)}$ ${\displaystyle (x,y)\wedge (z,w)=(x,w)}$ ${\displaystyle D}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle D}$ ${\displaystyle S/D}$ ${\displaystyle S}$ ${\displaystyle S}$

右手（左手）歪格子とキムラ因子分解

歪んだ格子が右手系であるとは、恒等写像または双対的にを満たす場合です。これらの恒等写像は本質的に、各- クラスで および が成り立つことを主張します。すべての歪んだ格子には、 と（または双対的にと）の場合に、合同性が で定義される一意の最大右手像があります。同様に、歪んだ格子が各 - クラスで と の場合、左手系です。また、歪んだ格子の最大左手像とは、合同性が に双対的に定義される像です。歪んだ格子の多くの例は、右手系または左手系です。合同写像の格子において、と は恒等写像 です。誘導エピモフィズムは、誘導エピモフィズムと の両方を介して因数分解されます。 を設定すると、で定義される準同型写像は、同型写像 を誘導します。これは、 をその最大右手像と左手像のファイバー積に キムラ因数分解したものです。${\displaystyle x\wedge y\wedge x=y\wedge x}$ ${\displaystyle x\vee y\vee x=x\vee y}$ ${\displaystyle x\wedge y=y}$ ${\displaystyle x\vee y=x}$ ${\displaystyle D}$ ${\displaystyle S}$ ${\displaystyle S/L}$ ${\displaystyle L}$ ${\displaystyle xLy}$ ${\displaystyle x\wedge y=x}$ ${\displaystyle y\wedge x=y}$ ${\displaystyle x\vee y=y}$ ${\displaystyle y\vee x=x}$ ${\displaystyle x\wedge y=x}$ ${\displaystyle x\vee y=y}$ ${\displaystyle D}$ ${\displaystyle S}$ ${\displaystyle S/R}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle R\vee L=D}$ ${\displaystyle R\cap L}$ ${\displaystyle \Delta }$ ${\displaystyle S\rightarrow S/D}$ ${\displaystyle S\rightarrow S/L}$ ${\displaystyle S\rightarrow S/R}$ ${\displaystyle T=S/D}$ ${\displaystyle k:S\rightarrow S/L\times S/R}$ ${\displaystyle k(x)=(L_{x},R_{x})}$ ${\displaystyle k*:S\sim S/L\times _{T}S/R}$ ${\displaystyle S}$

クリフォード・マクリーン定理と同様に、キムラ因数分解（または歪格子の第二分解定理）は、正則バンド（中吸収恒等式を満たすバンド）に対して初めて与えられました。実際、と はどちらも正則バンド演算です。上記の記号、、 は、もちろん基本的な半群論から来ています。^{[ 1 ] [ 3 ] [ 4 ] [ 5 ] [ 6 ] [ 7 ] [ 8 ] [ 9 ]}${\displaystyle xyxzx=xyzx}$ ${\displaystyle \wedge}$ ${\displaystyle \vee}$ ${\displaystyle D}$ ${\displaystyle R}$ ${\displaystyle L}$

歪格子の亜多様体

歪格子は多様体を形成します。長方形歪格子、左手系歪格子、右手系歪格子はすべて、歪格子の基本構造理論の中心となる亜多様体を形成します。以下にいくつか例を挙げます。

対称スキュー格子

歪んだ格子S が対称的である場合、任意の に対して であり、かつ である場合に限ります。したがって、このような歪んだ格子では交換の発生は一義的であり、互いに交換可能な元の部分集合は、交換可能な部分代数、すなわち部分格子を生成します。(これは一般に歪んだ格子には当てはまりません。) この部分多様体の等式基底は、Spinks ^{[ 10 ]}によって初めて示されました。およびです 。歪んだ格子の格子切断は、 の各-クラスが単一の元で出会うの部分格子です。したがって、 は格子の内部コピーであり、合成は同型です。 の対称な歪んだ格子はすべて、格子切断を許容します。^{[ 9 ]}対称であろうとなかろうと、格子断面を持つことは、 がおよびによってそれぞれ与えられるおよびの内部コピーを持つことを保証する。ここで、およびはにおけるおよび の合同類である。したがって、およびは同型である。^{[ 7 ]}これは、前述のキムラ図を双対化する埋め込みの可換図につながる。 ${\displaystyle x,y\in S}$ ${\displaystyle x\wedge y=y\wedge x}$ ${\displaystyle x\vee y=y\vee x}$ ${\displaystyle x\vee y\vee (x\wedge y)=(y\wedge x)\vee y\vee x}$ ${\displaystyle x\wedge y\wedge (x\vee y)=(y\vee x)\wedge y\wedge x}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle D}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle S/D}$ ${\displaystyle T\subseteq S\rightarrow S/D}$ ${\displaystyle |S/D|\leq \aleph _{0}}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle S/L}$ ${\displaystyle S/R}$ ${\displaystyle T[R]=\bigcup _{t\in T}R_{t}}$ ${\displaystyle T[L]=\bigcup _{t\in T}L_{t}}$ ${\displaystyle R_{t}}$ ${\displaystyle Lt}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle t}$ ${\displaystyle T}$ ${\displaystyle T[R]\subseteq S\rightarrow S/L}$ ${\displaystyle T[L]\subseteq S\rightarrow S/R}$

相殺的スキュー格子

歪格子は、 と が成り立ち、同様に と が成り立つとき、相殺的である。相殺的歪格子は対称であり、多様体を形成することが示される。格子とは異なり、相殺的である必要はなく、逆もまた同様である。 ${\displaystyle x\vee y=x\vee z}$ ${\displaystyle x\wedge y=x\wedge z}$ ${\displaystyle y=z}$ ${\displaystyle x\vee z=y\vee z}$ ${\displaystyle x\wedge z=y\wedge z}$ ${\displaystyle x=y}$

分配的歪格子

分配的歪格子は次の恒等式によって決定される。

${\displaystyle x\wedge (y\vee z)\wedge x=(x\wedge y\wedge x)\vee (x\wedge z\wedge x)}$ （D1）

${\displaystyle x\vee (y\wedge z)\vee x=(x\vee y\vee x)\wedge (x\vee z\vee x).}$ （D'1）

格子とは異なり、(D1)と(D'1)は一般には歪んだ格子に対しては同値ではないが、対称歪んだ格子に対しては同値である。^{[ 8 ] [ 11 ] [ 12 ]}条件(D1)は次のように強化することができる。

${\displaystyle x\wedge (y\vee z)\wedge w=(x\wedge y\wedge w)\vee (x\wedge z\wedge w)}$ （D2）

この場合、(D'1)は帰結である。歪格子が(D2)とその双対であるを満たすのは、それが分配格子と直角歪格子の積として因数分解できる場合のみである。後者の場合、(D2)は次のように強化できる。 ${\displaystyle S}$ ${\displaystyle x\vee (y\wedge z)\vee w=(x\vee y\vee w)\wedge (x\vee z\vee w)}$

${\displaystyle x\wedge (y\vee z)=(x\wedge y)\vee (x\wedge z)}$ そして。（D3） ${\displaystyle (y\vee z)\wedge w=(y\wedge w)\vee (z\wedge w)}$

(D3)は、それ自体では、対称性が追加された(D2)と同等である。^{[ 1 ]}したがって、(D1)、(D2)、(D3)とそれらの双対によってそれぞれ決定される6つの歪格子のサブ多様体が得られる。

法線スキュー格子

上で見たように、と は恒等式 を満たす。より強い恒等式 を満たす帯は正規帯と呼ばれる。歪んだ格子は、 を満たすとき正規歪んだ格子である。 ${\displaystyle \wedge}$ ${\displaystyle \vee}$ ${\displaystyle xyxzx=xyzx}$ ${\displaystyle xyzx=xzyx}$

${\displaystyle x\wedge y\wedge z\wedge x=x\wedge z\wedge y\wedge x.(N)}$

正規歪格子 の各元 a について、 { } またはそれと同等の { }で定義される集合はの部分格子であり、その逆も同様です。(したがって、正規歪格子は局所格子とも呼ばれます。) と が両方とも正規である場合、は格子と直角歪格子の積に同型に分割され、その逆も同様です。したがって、正規歪格子と分割歪格子はどちらも多様体を形成します。分布に戻ると、は分配正規歪格子の多様体を特徴付け、(D3) は対称分配正規歪格子の多様体を特徴付けます。 ${\displaystyle S}$ ${\displaystyle a\wedge S\wedge a}$ ${\displaystyle a\wedge x\wedge a|x\in S}$ ${\displaystyle x\in S|x\leq a}$ ${\displaystyle S}$ ${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle S}$ ${\displaystyle T\times D}$ ${\displaystyle T}$ ${\displaystyle D}$ ${\displaystyle (D2)=(D1)+(N)}$ ${\displaystyle (D2)}$

カテゴリカル歪格子

歪んだ格子は、剰余類一対一の空でない合成物が剰余類一対一であるとき、圏的である。圏的歪んだ格子は多様体を形成する。環内の歪んだ格子や正規歪んだ格子はこの多様体の代数の例である。[ ^{3 ] 、}をからへ取る剰余類一対一、を からへ取る剰余類一対一、をから へ取る剰余類一対一、最後にからへ取る剰余類一対一とする。歪んだ格子が圏的であるとは、常に等式 が成り立つこと、すなわち が成り立つこと、つまり が空でないときの合成部分一対一がの剰余類から の剰余類への剰余類一対一である場合である。すなわち である。分配的歪んだ格子はすべて圏的である。ただし対称歪んだ格子はそうではないかもしれない。ある意味では、それらは対称性と分配性の特性間の独立性を明らかにする。^{[ 1 ] [ 3 ] [ 5 ] [ 8 ] [ 9 ] [ 10 ] [ 12 ] [ 13 ]}${\displaystyle a>b>c}$ ${\displaystyle a\in A}$ ${\displaystyle b\in B}$ ${\displaystyle c\in C}$ ${\displaystyle \varphi }$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \psi }$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle \chi }$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle a}$ ${\displaystyle c}$ ${\displaystyle S}$ ${\displaystyle \psi \circ \varphi =\chi }$ ${\displaystyle \psi \circ \varphi }$ ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle (A\wedge b\wedge A)\cap (C\vee b\vee C)=(C\vee a\vee C)\wedge b\wedge (C\vee a\vee C)=(A\wedge c\wedge A)\vee b\vee (A\wedge c\wedge A)}$

歪んだブール代数

歪格子Sの零元とは、 Sの元0であって、すべての場合、あるいは双対的に、(0) ${\displaystyle x\in S,}$ ${\displaystyle 0\wedge x=0=x\wedge 0}$ ${\displaystyle 0\vee x=x=x\vee 0.}$

ブール歪格子は、0 を持つ対称で分配的な正規歪格子であり、各 に対してブール格子となる。このような歪格子Sが与えられたとき、差分演算子 \ は x \ y = で定義され、後者はブール格子^{[ 1 ]}で評価される。(D3) および (0) が存在する場合、\ は次の恒等式で特徴付けられる。 ${\displaystyle (S;\vee ,\wedge ,0),}$ ${\displaystyle a\wedge S\wedge a}$ ${\displaystyle a\in S.}$ ${\displaystyle x-x\wedge y\wedge x}$ ${\displaystyle x\wedge S\wedge x.}$

${\displaystyle y\wedge x\setminus y=0=x\setminus y\wedge y}$ および（SB） ${\displaystyle (x\wedge y\wedge x)\vee x\setminus y=x=x\setminus y\vee (x\wedge y\wedge x).}$

したがって、恒等式 (D3)、(0)、(SB) で特徴付けられる様々な歪ブール代数が得られる。原始歪ブール代数は、0 と単一の非 0 Dクラスから構成される。したがって、の場合、 、それ以外 の場合、 (0) を介して0 を長方形歪格子Dに付加した結果である。すべての歪ブール代数は原始代数の直積である。歪ブール代数は、ブール挙動の普遍代数における判別子多様体やその他の一般化の研究において重要な役割を果たす。 ^{[ 14 ] [ 15 ] [ 16 ] [ 17 ] [ 18 ] [ 19 ] [ 20 ] [ 21 ] [ 22 ] [ 23 ] [ 24 ]}${\displaystyle (S;\vee ,\wedge ,\,0)}$ ${\displaystyle x\setminus y=x}$ ${\displaystyle y=0}$ ${\displaystyle 0}$

リング内の斜め格子

を環とし 、内のすべてのべき等元からなる集合を とします。すべての集合およびに対して、 となります。 ${\displaystyle A}$ ${\displaystyle E(A)}$ ${\displaystyle A}$ ${\displaystyle x,y\in A}$ ${\displaystyle x\wedge y=xy}$ ${\displaystyle x\vee y=x+y-xy}$

明らかにですが、 も結合的です。 および の部分集合が で閉じている場合、は分配的かつ相殺的な歪んだ格子です。におけるこのような歪んだ格子を見つけるには、 のバンド、特に何らかの制約に関して最大​​のものを調べます。実際、 における右正則 (= ) であることに関して最大​​のすべての乗法バンドは、 においても閉じているため、右手歪んだ格子を形成します。一般に、 のすべての右正則バンドは、において右手歪んだ格子を生成します。 における左正則バンド (恒等式 を満たすバンド)についても双対的な注釈が成り立ちます。最大正則バンドは、定義されているように で閉じている必要はありません。反例は、乗法長方形バンドを使用すれば簡単に見つかります。ただし、これらの場合は が に簡約されて、双対長方形バンドを与えるため、によって定義されるの 3 次変形の下では閉じています。正則性の条件を正規性 に置き換えると、におけるすべての最大正規乗法バンドはについても閉じており、 はブール歪格子を形成する。自身が乗法について閉じている場合、それは正規バンドであり、したがってブール歪格子を形成する。実際、任意の歪ブール代数はこのような代数に埋め込むことができる。^{[ 25 ]} A が乗法単位元 を持つ場合、 が乗法的に閉じているという条件は、がブール代数を形成することを意味することがよく知られている。 環における歪格子は、引き続き良い例と動機付けの源となっている。^{[ 22 ] [ 26 ] [ 27 ] [ 28 ] [ 29 ]}${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle S\subseteq E(A)}$ ${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle (S,\wedge ,\vee )}$ ${\displaystyle E(A)}$ ${\displaystyle E(A)}$ ${\displaystyle ()}$ ${\displaystyle \vee }$ ${\displaystyle E(A)}$ ${\displaystyle E(A)}$ ${\displaystyle xyx=xy}$ ${\displaystyle E(A)}$ ${\displaystyle \vee }$ ${\displaystyle \vee }$ ${\displaystyle x\nabla y=x+y+yx-xyx-yxy}$ ${\displaystyle x\nabla y}$ ${\displaystyle yx}$ ${\displaystyle (xyzw=xzyw)}$ ${\displaystyle S}$ ${\displaystyle E(A)}$ ${\displaystyle \nabla }$ ${\displaystyle (S;\wedge ,\vee ,/,0)}$ ${\displaystyle x/y=x-xyx}$ ${\displaystyle E(A)}$ ${\displaystyle 1}$ ${\displaystyle E(A)}$ ${\displaystyle E(A)}$

プリミティブスキュー格子

ちょうど2つのDクラスからなる歪んだ格子は原始歪んだ格子と呼ばれる。に-クラスを持つ歪んだ格子が与えられたとき、任意の および に対して、部分集合 ${\displaystyle S}$ ${\displaystyle D}$ ${\displaystyle A>B}$ ${\displaystyle S/D}$ ${\displaystyle a\in A}$ ${\displaystyle b\in B}$

${\displaystyle A\wedge b\wedge A=}$ { } そして { }${\displaystyle u\wedge b\wedge u:u\in A}$ ${\displaystyle \subseteq B}$ ${\displaystyle B\vee a\vee B=}$ ${\displaystyle v\vee a\vee v:v\in B}$ ${\displaystyle \subseteq A}$

はそれぞれ、A の B における剰余類、およびB の A における剰余類と呼ばれます。これらの剰余類は、B と A を および で分割します。剰余類は常にその -類において直角部分代数です。さらに、半順序は、次式で定義される剰余類一対一を誘導します。 ${\displaystyle b\in A\wedge b\wedge A}$ ${\displaystyle a\in B\wedge a\wedge B}$ ${\displaystyle D}$ ${\displaystyle \geq }$ ${\displaystyle \varphi :B\vee a\vee B\rightarrow A\wedge b\wedge A}$

${\displaystyle \phi (x)=y}$ の場合 、およびの場合も同様です。 ${\displaystyle x>y}$ ${\displaystyle x\in B\vee a\vee B}$ ${\displaystyle y\in A\wedge b\wedge A}$

全体として、剰余類一対一は部分集合との間を記述します。また、異なる -クラスの元のペアに対してと を決定します。実際、 と が与えられたとき、との剰余類間のコスト一対一を とします。すると、 ${\displaystyle \geq }$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \vee }$ ${\displaystyle \wedge }$ ${\displaystyle D}$ ${\displaystyle a\in A}$ ${\displaystyle b\in B}$ ${\displaystyle \varphi }$ ${\displaystyle B\vee a\vee B}$ ${\displaystyle A}$ ${\displaystyle A\wedge b\wedge A}$ ${\displaystyle B}$

${\displaystyle a\vee b=a\vee \varphi -1(b),b\vee a=\varphi -1(b)\vee a}$ そして。 ${\displaystyle a\wedge b=\varphi (a)\wedge b,b\wedge a=b\wedge \varphi (a)}$

一般に、およびが与えられ、 および の場合、 の共通-剰余類に属し、の共通- 剰余類に属するのは、 の場合のみである。したがって、各剰余類一対一は、ある意味では、互いに平行なペア の最大の集合である。 ${\displaystyle a,c\in A}$ ${\displaystyle b,d\in B}$ ${\displaystyle a>b}$ ${\displaystyle c>d}$ ${\displaystyle a,c}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle b,d}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle a>b//c>d}$ ${\displaystyle a>b}$

すべての原始歪格子は、その左手および右手の最大原始像のファイバー積として因数分解されます。右手原始歪格子は次のように構成されます。 と を互いに素な空でない集合 と の分割とし、すべての と は同じ大きさを共有します。各ペアについて、からへの固定された一対一写像を取ります。 とをそれぞれ と と とします。ただし、 と が与えられた場合、とと をそれぞれ設定します。 ${\displaystyle S}$ ${\displaystyle S/R\times _{2}S/L}$ ${\displaystyle A=\cup _{i}A_{i}}$ ${\displaystyle B=\cup _{j}B_{j}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A_{i}}$ ${\displaystyle B_{j}}$ ${\displaystyle i,j}$ ${\displaystyle \varphi _{i},j}$ ${\displaystyle A_{i}}$ ${\displaystyle B_{j}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle x\wedge y=y}$ ${\displaystyle x\vee y=x}$ ${\displaystyle a\in A}$ ${\displaystyle b\in B}$

${\displaystyle a\vee b=a,b\vee a=a',a\wedge b=b}$ そして${\displaystyle b\wedge a=b'}$

ここで、および はのセルに属し、は のセルに属します。様々な は剰余類単射です。これは次の部分ハッセ図で示されます。ここで、矢印はおよびからの-出力とを示します。 ${\displaystyle \varphi _{i,j}(a')=b}$ ${\displaystyle \varphi _{i,j}(a)=b'}$ ${\displaystyle a'}$ ${\displaystyle A_{i}}$ ${\displaystyle a}$ ${\displaystyle b'}$ ${\displaystyle B_{j}}$ ${\displaystyle b}$ ${\displaystyle \varphi i,j}$ ${\displaystyle |A_{i}|=|B_{j}|=2}$ ${\displaystyle \varphi _{i,j}}$ ${\displaystyle \geq }$ ${\displaystyle A}$ ${\displaystyle B}$

左手系プリミティブスキュー格子は双対的な方法で構築されます。すべての右手系[左手系]プリミティブスキュー格子はこの方法で構築できます。^{[ 1 ]}

歪格子の剰余類構造

非直角歪格子はその最大原始歪格子で覆われる:における比較可能な-クラスが与えられると、の最大原始部分代数を形成し、におけるすべての-クラスはそのような部分代数に含まれる。これらの原始部分代数上の剰余類構造は、少なくともとが の下で比較可能な場合に、結果 と を決定するために組み合わされる。と は一般に剰余類とその全単射によって決定されるが、-比較可能な場合ほど直接的ではないことがわかる。特に、においてDクラスJが結合しDクラスと出会う2 つの比較不可能なDクラス A と Bが与えられると、A と B に関する J (または M) の 2 つの剰余類分解の間に興味深い関係が生じる。^{[ 3 ]}${\displaystyle S}$ ${\displaystyle D}$ ${\displaystyle A>B}$ ${\displaystyle S/D}$ ${\displaystyle A\cup B}$ ${\displaystyle S}$ ${\displaystyle D}$ ${\displaystyle S}$ ${\displaystyle x\vee y}$ ${\displaystyle x\wedge y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \preceq }$ ${\displaystyle x\vee y}$ ${\displaystyle x\wedge y}$ ${\displaystyle \preceq }$ ${\displaystyle M}$ ${\displaystyle S/D}$

したがって、歪んだ格子は、格子の頂点に置かれた長方歪んだ格子の剰余類アトラスと、それらの間の剰余類一対一と考えることができます。後者は、各剰余類一対一が対応する剰余類のペアを決定する長方代数間の部分同型として見ることができます。この見方は、本質的には歪んだ格子のハッセ図を与え、それは比較的小さい次数の場合には簡単に描くことができます。(上のセクション 3 の図を参照してください。)におけるDクラスの連鎖が与えられると、A から B、B から C、A から C の 3 つの剰余類一対一集合が与えられます。一般に、剰余類一対一と が与えられると、部分一対一の合成は空になる可能性があります。そうでない場合、 となる唯一の剰余類一対一が存在します。(繰り返しますが、はとにおける剰余類のペア間の一対一です。) この包含は厳密になる可能性があります。与えられた歪格子S上で、 Sが圏的であるとき、それは常に（ が与えられている）等式となる。この場合、各直方体D -クラス上の恒等写像と、適切に比較可能なD -クラス間の隣接する空単射を含めることで、直方体代数とそれらの間の剰余類単射の圏が得られる。第3節の簡単な例は圏的である。 ${\displaystyle A>B>C}$ ${\displaystyle S/D}$ ${\displaystyle \varphi :A\rightarrow B}$ ${\displaystyle \psi :B\rightarrow C}$ ${\displaystyle \psi \varphi }$ ${\displaystyle \chi :A\rightarrow C}$ ${\displaystyle \psi \varphi \subseteq \chi }$ ${\displaystyle \chi }$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle \psi \varphi \neq \emptyset }$

参照

• 半群論
• 格子理論

参考文献

1. リーチ、J、「リング内の斜め格子」、アルジェブラ・ユニバーサリス、26（1989）、48-72
2. Jordan、P. Uber Nichtkommutative Verbände、Arch.数学。 2 (1949)、56–59。
3. Leech, J, 斜め格子理論の最近の発展、セミグループフォーラム、52(1996)、7-24。
4. Leech, J.、「魔方陣、有限平面、単純準格子」、Ars Combinatoria 77(2005)、75-96。
5. Leech, J, 斜め格子の幾何学、セミグループフォーラム、52(1993)、7-24。
6. Leech, J, 正規歪格子、セミグループフォーラム、44(1992)、1-8。
7. Cvetko-Vah, K, 歪格子の内部分解、Communications in Algebra、35 (2007)、243-247
8. Cvetko-Vah, K. Spinksの定理の新しい証明、Semigroup Forum 73 (2006), 267-272。
9. Laslo, G および Leech, J、「非可換格子上のグリーン関係」、Acta Sci. Math. (Szeged)、68 (2002)、501-533。
10. Spinks, M, 非可換格子理論における自動演繹、技術レポート3/98、モナッシュ大学、GSCIT、1998
11. Spinks, M, 非可換格子理論における自動演繹、技術レポート3/98、モナッシュ大学ギップスランドコンピューティング情報技術学部、1998年6月
12. Spinks, M, 歪格子の中分布性について、Semigroup Forum 61 (2000), 341-345。
13. ツヴェトコ＝ヴァ、カリン ;キニヨン、M. ;リーチ、J. ; Spinks、M.スキュー格子におけるキャンセル。注文28 (2011)、9-32。
14. Bignall, RJ、「準原始多様体と普遍代数の成分」、博士論文、南オーストラリア州フリンダース大学、1976 年。
15. Bignall, RJ、「非可換多値論理」、Proc. 21st International Symposium on Multiple-valued Logic、1991年、IEEE Computer Soc. Press、49-54。
16. Bignall, RJ および J Leech、「Skew Boolean algebras and discriminator variety」、Algebra Universalis、33 (1995)、387-398。
17. Bignall, RJおよびM Spinks、「命題的スキューブール論理」、Proc. 26th International Symposium on Multiple-valued Logic、1996年、IEEE Computer Soc. Press、43-48。
18. Bignall、RJ および M Spinks、 Implicative BCS-algebra subreducts of skew Boolean algebras、Scientiae Mathematicae Japonicae、58 (2003)、629-638。
19. Bignall, RJ および M Spinks、「バイナリ識別器多様体について (I): 暗黙的 BCS 代数」、 International Journal of Algebra and Computation、近日公開予定。
20. Cornish, WH, ブール歪代数, Acta Math. Acad. Sci. Hung. , 36 (1980), 281-291.
21. Leech, J, 歪んだブール代数、Algebra Universalis、27(1990)、497-506。
22. LeechとSpinks、一般化ブール代数から生成されたSkewブール代数、Algebra Universalis 58 (2008)、287-302、307-311。
23. Spinks, M、「Pre-BCK代数理論への貢献」、モナッシュ大学学位論文、2002年。
24. Spinks, M および R Veroff、「歪んだブール命題計算の公理化」、J. Automated Reasoning、37 (2006)、3-20。
25. Cvetko-Vah, K, 行列環内の斜め格子、Algebra Universalis 53 (2005), 471-479。
26. Cvetko-Vah, K, リング内の純粋な斜め格子、 Semigroup Forum 68 (2004), 268-279。
27. Cvetko-Vah、K、Pure ∇-bands、セミグループ フォーラム71 (2005)、93-101。
28. Cvetko-Vah、K、リング内のスキュー格子、論文、リュブリャナ大学、2005 年。
29. Cvetko-Vah, K and J Leech, 環のバンドにおける∇演算の結合性, Semigroup Forum 76 (2008), 32-50