大きな欠片二菱十二面体
| 大きな欠片二菱十二面体 | |
|---|---|
 | |
| タイプ | 均一な星型多面体 |
| 要素 | F = 204、E = 360 V = 60 (χ = −96) |
| 側面の顔 | 120{3}+60{4}+24{5/2} |
| コクセター図 | {{{スキルリング・コクセター}}} |
| ウィトフ記号 | | (3/2) 5/3 (3) 5/2 |
| 対称群 | 私はh、[5,3]、*532 |
| 索引参照 | U -、C -、W - |
| 二重多面体 | グレートディスナブディロンビドデカクロン |
| 頂点図形 |  (5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/ 2 (5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/ 2 |
| バウアーズの頭字語 | ギディスドリッド |

幾何学において、大不等辺二菱十二面体(スキリング図形とも呼ばれる)は、縮退した均一な星型多面体である。
1970年、プリズムと反プリズムの無限族を除いて、均一な多面体はわずか75種類しか存在しないことが証明されました。ジョン・スキリングは、辺が単一でなければならないという条件を緩和することで、もう一つの退化した例、すなわち、大きな不連続な二菱形十二面体を発見しました。[ 1 ]より正確には、彼は面の集合が2つの連結した集合に分割されない限り、各辺で任意の偶数個の面が接することを許容しました。幾何学的に実現すると、4つの面が接する二重辺がいくつか存在するため、厳密には均一な多面体ではなく、むしろ退化した均一な多面体と見なされます。
辺の数は曖昧です。なぜなら、基礎となる抽象多面体には360本の辺がありますが、幾何学的実現ではそのうち120組の辺が同じ像を持つため、幾何学的実現では単辺が120本、4面が交わる二重辺が120本、合計240本の辺を持つことになります。抽象多面体のオイラー標数は-96です。幾何学的実現における一致する辺の組を単辺とみなすと、多面体の辺は240本となり、オイラー標数は24となります。
頂点図形には、モデルの中心を通る 4 つの正方形の面があります。
これは、大二菱十二面体と20 個の八面体の化合物の排他的論理和(ブレンド)として構築できます。
関連する多面体
大きな二菱形十二面体と同じ辺の配置ですが、三角形の面の集合が異なります。頂点と辺は、20個の八面体または20個の四半六面体からなる均一な複合体とも共通です。180個の辺は、大きなスナブ十二二面体と共通です。
 凸包 凸包 |  グレートスナブ・ドデカシドデカヘドロン グレートスナブ・ドデカシドデカヘドロン | 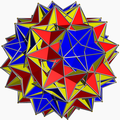 大二菱形十二面体 大二菱形十二面体 |
 大きな欠片二菱十二面体 大きな欠片二菱十二面体 |  20個の八面体の複合体 20個の八面体の複合体 |  20個の四半六面体の複合体 20個の四半六面体の複合体 |
二重多面体

大不等辺二菱形十二面体の双対は大不等辺二菱形十二面体と呼ばれる。これは非凸無限等面体多面体である。
マグナス・ヴェニンガーの『双対モデル』に登場する視覚的に同一の大二菱形十二面体と同様に、この図形は、モデルの中心を通る交差する無限の柱状体で表現され、製作者にとって都合の良い特定の点で切断されている。ヴェニンガーは、これらの図形が「無限への星状化」と呼ばれる新しい種類の星状多面体の一種であると示唆した。しかし、彼はまた、その構成が通常の定義に従わないため、厳密には多面体ではないことも認めている。
ギャラリー
 伝統的な詰め物 伝統的な詰め物 |  モジュロ2充填 モジュロ2充填 |
参照
参考文献
- スキルリング、ジョン(1975)「均一多面体の完全集合」、王立協会哲学論文集A、278(1278):111– 135、Bibcode:1975RSPTA.278..111S、doi:10.1098/rsta.1975.0022、JSTOR 74475。
- ワイスタイン、エリック W. 「大二菱形十二面体」。MathWorld 。
- ウェッブ、ロバート (2001). 「大菱形十二面体(「ミラーの怪物」)」ステラ.
外部リンク
- 多面体からのスキルリング図形ジム・マクニール
- ジョージ・W・ハート著『仮想多面体』より「大ディスナブ二菱十二面体」