小型複二十面体
 |
| 小型複合二十面体 | |
|---|---|
 | |
| 種類 | 均一な星型多面体 |
| 要素 | F = 32、E = 60 (30x2) V = 12 (χ = −16) |
| 面と辺 | 20{3}+12{5} |
| コクセター図 |     |
| ウィトフ記号 | 5 | 3/2 5 |
| 対称群 | I h , [5,3], *532 |
| 索引参照 | U -、C -、W - |
| 双多面体 | 小型複二十面体 |
| 頂点図形 | 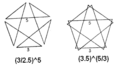 (3 / 2.5) 5 (3.5) 5/3 (3 / 2.5) 5 (3.5) 5/3 |
| バウアーズの頭字語 | シド |
幾何学において、小型複素二十面体(イコシドデカヘドロンは)退化した均一な星型多面体です。辺が2倍になっているため、退化しています。星型は32面(20の三角形と12の五角形)、60(2倍)の辺、12の頂点、4つの共有面を持ちます。位相多面体として、これらの面は2つの重なり合う辺として扱われます
多数の異なる頂点図形から、小さく複雑な二十面体を構築できます。
非常によく似た図形が、大星型十二面体の幾何学的切断として現れます。五芒星の面は二重に巻かれた五角形 ({5/2} --> {10/2}) となり、内部は五角形の平面となり、各頂点で交わる 3 つの点は三角形となり、外部は三角形の平面となります。
複合体として
小型複二十面体は、すべての頂点が正確で辺が一致する二十面体{3,5}と大十二面体{5,5/2}の複合体と見ることができます。小型複二十面体は二十面体に似ています。なぜなら、大十二面体は二十面体の中に完全に収まっているからです
 |  |  |
| 二十面体 | 大十二面体 | 複合 |
2次元における類似体は、正五角形{5}(イコサヘドロンをn次元五角形多面体として表す)と正五芒星{5/2}(n次元星型)の合成体となる。これらの形状は、3次元における類似体が辺を共有するのと同様に、頂点を共有する。
 |  |  |
| 五角形 | 五芒星形 | 複合 |
参照
参考文献
- コクセター、ハロルド・スコット・マクドナルド;ロンゲット=ヒギンズ、MS;ミラー、JCP (1954)、「均一多面体」、ロンドン王立協会哲学論文集。シリーズA。数学および物理科学、246 (916): 401– 450、Bibcode : 1954RSPTA.246..401C、doi : 10.1098/rsta.1954.0003、ISSN 0080-4614、JSTOR 91532、MR 0062446、S2CID 202575183(表6、退化した症例)
- Weisstein, Eric W. 「小型複素二十面体」MathWorld。
- Klitzing, Richard. 「3D均一多面体 x3/2o5o5*a - cid」。

