ソナー信号処理

水中音響信号処理

ソナーシステムは、一般的に水中で距離測定や探知に使用されます。アクティブソナーは、音響信号、つまり音波を水中に発信します。音は目標物に反射し、ソナートランスデューサーにエコーを返します。アクティブソナーとは異なり、パッシブソナーは独自の信号を発信しないため、軍艦には有利です。しかし、パッシブソナーは、他のパッシブリスニングデバイスと組み合わせて使用しないと、物体の距離を測定できません。音源の三角測量には、複数のパッシブソナーデバイスを使用する必要があります。アクティブソナーであれパッシブソナーであれ、反射信号に含まれる情報は、技術的な信号処理なしでは使用できません。混合信号から有用な情報を抽出するには、生の音響データを転送するためのいくつかの手順が実行されます。

アクティブソナー

アクティブソナーの場合、信号処理システム中に 6 つのステップが必要です。

信号生成

信号パルスを生成するための典型的なアナログ実装は、発振器と電圧制御発振器（VCO）であり、その後に変調器が接続されます。振幅変調は、パルスの包絡線に重み付けを行い、信号スペクトルを伝送に適した搬送周波数まで変換するために使用されます。

まず、ソナーシステムでは、音圧場はと表すことができます。この場関数は、時間と空間座標の4つの変数を含みます。したがって、フーリエ変換によれば、周波数領域では^[1] $s(t,{\vec {r}})$ $t$ ${\vec {r}}=(x,y,z)$

${\begin{aligned}s(w,{\vec {k}})&=\iiiint s(t,{\vec {r}})\cdot e^{-j(wt-{\vec {k}}{\vec {r}})}d{\vec {x}}\,dt,\\{\vec {k}}&=(k_{x},k_{y},k_{z}),\\s(t,{\vec {r}})&=\iiiint s(w,{\vec {k}})\cdot e^{j(wt-{\vec {k}}{\vec {r}})}d{\vec {k}}\,dw,\end{aligned}}$

式中のは時間周波数、は空間周波数です。任意の4次元信号は要素信号の線形結合によって生成できるため、を要素信号と定義することがよくあります。明らかに、の方向は波の伝播方向を示し、波の速度は $w$ ${\vec {k}}$ $s(t,{\vec {r}})=e^{-j(wt-{\vec {k}}{\vec {r}})},$ ${\vec {k}}$

$v={\frac {w}{|{\vec {k}}|}}$

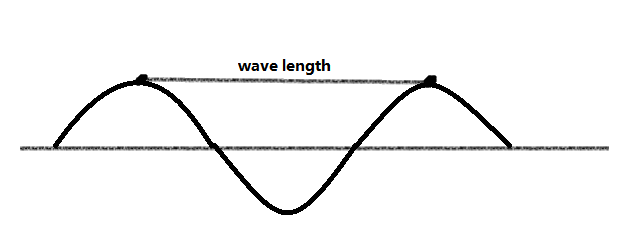
波長は $\lambda ={\frac {2\pi }{|{\vec {k}}|}}$

時間的サンプリング

現代社会において、デジタルコンピュータはデータ分析の高速化と効率化に大きく貢献しています。そのため、アナログ信号を時間領域でサンプリングし、デジタル信号に変換することが必要になります。この処理は、デジタル変換デバイス、ダイナミックレンジコントローラ、そしてデジタル変換デバイスの3つのデバイスによって実現されます。

簡略化のため、サンプリングは等間隔で行われる。サンプリングされた信号から信号を再構成した後に生じる歪み（周波数領域におけるエイリアシング）を防ぐには、より高速なサンプリングレートでサンプリングする必要がある。アナログ信号の情報量を良好に保持できるサンプリングレートは、ナイキスト・シャノンのサンプリング定理に従う。サンプリング周期をTとすると、時間的サンプリング後の信号は $s(t,{\vec {r}})$

$r(t)=r(nT)=s({\vec {r}},nT)$ n は整数です。

空間サンプリングとビームフォーミング

ソナーシステムにおいて良好なシステム性能を得るには、適切なセンサーアレイとビームフォーマーを備えることが非常に重要です。音響場に関する情報を推測するには、空間と時間の両方で音場をサンプリングする必要があります。時間サンプリングについては、前のセクションで既に説明しました。センサーアレイは空間領域をサンプリングし、ビームフォーマーはセンサーの出力を特殊な方法で統合することで、システムの検出性能と推定性能を向上させます。ビームフォーマーへの入力は時系列データであり、ビームフォーマーの出力は別の時系列データまたはフーリエ係数データです。

$r_{i}(t)=s({\vec {x}}_{i},t)$

${\vec {x}}_{i}=(x_{i},0,0)=(iD,0,0)$

希望する方向については、を設定します。 ${\vec {k}}={\vec {k}}_{0}$ $t_{i}={\frac {{\vec {k}}_{0}}{w}}{\vec {x}}_{i}$

ビームフォーミングは、特定の方向に伝播する信号成分を分離するために適用できるフィルタリングの一種です。図は、最も単純なビームフォーマーである重み付け遅延加算ビームフォーマーを示しています。これは、受信機またはセンサーのアレイによって実現できます。各三角形は、空間領域でサンプリングするセンサーです。空間サンプリング後、サンプル信号は重み付けされ、結果はすべての重み付けされた信号を加算したものです。空間に分散されたM個のセンサーアレイを想定し、番目のセンサーが位置に配置され、そのセンサーによって受信される信号がで示されるとします。したがって、ビームフォーミング後の信号は $i$ $x_{i}(i=0,1,...,M-1)$ $r_{i}(t)$

$b(t)={\frac {1}{M}}\sum _{i=0}^{i=M-1}{w_{i}r_{i}(t-t_{i})}$

バンドシフト

アクティブソナーとパッシブソナーでは、後続処理に必要なハードウェアとソフトウェアの複雑さを軽減するために、バンドシフトが採用されています。例えば、アクティブソナーでは、受信信号は通常約2kHzの非常に狭い周波数帯域に収まっており、中心周波数は通常約50kHzの高周波数です。受信信号を100kHzのナイキスト周波数でサンプリングする必要がないように、受信信号をベースバンドに復調し、その後、複素包絡線を2kHzでのみサンプリングする方が効率的です。

フィルタリングとスムージング

現代のソナーシステムでは、フィルタとスムージングが広く使用されています。サンプリング後、信号はアナログ信号から離散時間信号に変換されるため、デジタルフィルタが考慮されることになります。さらに、一部のフィルタは時間可変または適応型ですが、ほとんどのフィルタは線形シフト不変です。ソナー信号プロセッサで使用されるデジタルフィルタは、波形のフィルタリングによる周波数成分の調整と、波形のスムージングによるノイズの影響の低減という2つの主要な機能を実行します。デジタルフィルタには、FIRフィルタと無限インパルス応答（IIR）フィルタの2種類があります。FIRフィルタの入出力関係は次のとおりです。

$y(n)=\sum _{k=0}^{N-1}{h(k)x(nk)}$ （1-D）

$y(n1,n2)=\sum _{k_{1}=0}^{M_{1}-1}\sum _{k_{2}=0}^{M_{2}-1}{h(k_{1},k_{2})x(n_{1}-k_{1},n_{2}-k_{2})}$ （2次元）

IIRフィルタの入出力関係は

$y(n)=\sum _{k=0}^{N-1}{a_{k}x(nk)}+\sum _{k=0}^{M-1}{b_{k}y(nk)}$ （1-D）

$y(n_{1},n_{2})=\sum _{r_{1}=0}^{N_{1}-1}\sum _{r_{2}=0}^{N_{2}-1}{a(r_{1},r_{2})x(n_{1}-r_{1},n_{2}-r_{2})}-\sum _{l_{1}=0}^{M_{1}-1}\sum _{l_{2}=0}^{M_{2}-1}{b(l_{1},l_{2})y(l_{1},l_{2})}$ （2次元）

FIRフィルタとIIRフィルタはそれぞれ長所と短所があります。第一に、FIRフィルタを実装する場合、ソナープロセッサの計算要件はより厳しくなります。第二に、IIRフィルタでは線形位相を得るのが常に難しいため、FIRフィルタはIIRフィルタよりも安定しています。さらに、FIRフィルタはウィンドウ処理を用いてより容易に設計できます。

意思決定処理

一言で言えば、ソナーの目的は、音響空間時間場から情報とデータを抽出し、それらを設計・規定されたプロセスに組み込むことで、様々なケースを一つの固定パターンに適用できるようにすることです。この目的を実現するために、ソナーシステムの最終段階は以下の機能で構成されています。

検出:ソナー検出により、ターゲットの周囲にノイズがあるかどうかを判断します。
分類:ソナー分類は検出されたターゲット信号を区別します。
パラメータ推定と追跡:ソナーにおける推定は、すでに検出されたターゲットの位置特定と関連することがよくあります。
正規化: 正規化は、検出統計のノイズのみの応答を可能な限り均一にすることです。
表示処理:表示処理は、ソナーシステムの操作性とデータ管理の問題に対処します。

参照

参考文献

^ Mazur, Martin. ソナー信号処理(PDF) . ペンシルベニア州立大学応用研究研究所. p. 14.

ウィリアム・C・ナイト. ソナーのためのデジタル信号処理. IEEE PROCEEDINGS. Vol-69. No-11, 1981年11月
ホセイン・ペイヴァンディ。ソナーシステムと水中信号処理：古典的アプローチと現代的アプローチ。科学応用電気通信大学、テヘラン。

[1] Mazur, Martin. ソナー信号処理(PDF) . ペンシルベニア州立大学応用研究研究所. p. 14.