対称的減少転位

数学において、関数の対称減少再配置とは、対称かつ減少する関数であり、そのレベルセットは元の関数と同じサイズである。^[1]

集合の定義

測定可能な集合が与えられたとき、の対称的な再配置をと呼ぶ。この再配置は原点を中心とする球体であり、その体積（ルベーグ測度）は集合 の体積と同じである。${\displaystyle A,}$ ${\displaystyle \mathbb {R} ^{n},}$ ${\displaystyle A,}$ ${\displaystyle A^{*},}$ ${\displaystyle A.}$

同等の定義は、 単位球の体積は どこであり、単位球の体積はどこである。$${\displaystyle A^{*}=\left\{x\in \mathbb {R} ^{n}:\,\omega _{n}\cdot |x|^{n}<|A|\right\},}$$ ${\displaystyle \omega _{n}}$ ${\displaystyle |A|}$ ${\displaystyle A.}$

関数の定義

非負で測定可能な実数値関数の並べ替えは、（ に対して） 準位集合が有限測度を持つ場合、 となる。 ここで は集合の指示関数を表す。 つまり、 の値は、 の対称並べ替えの半径が に等しい高さを与える。この定義には、次のような動機がある。任意 の非負関数に対して恒等式が成り立つため、上記の定義は、恒等式が成り立つことを強制する唯一の定義である。 ${\displaystyle f}$ ${\displaystyle f^{-1}(y)}$ ${\displaystyle y\in \mathbb {R} _{\geq 0}}$ $${\displaystyle f^{*}(x)=\int _{0}^{\infty }\mathbb {I} _{\{y:f(y)>t\}^{*}}(x)\,dt,}$$ ${\displaystyle \mathbb {I} _{A}}$ ${\displaystyle A.}$ ${\displaystyle f^{*}(x)}$ ${\displaystyle t}$ ${\displaystyle \{y:f(y)>t\}}$ ${\displaystyle x.}$ $${\displaystyle g(x)=\int _{0}^{\infty }\mathbb {I} _{\{y:g(y)>t\}}(x)\,dt,}$$ ${\displaystyle g,}$ ${\displaystyle \mathbb {I} _{A}^{*}=\mathbb {I} _{A^{*}}}$

プロパティ

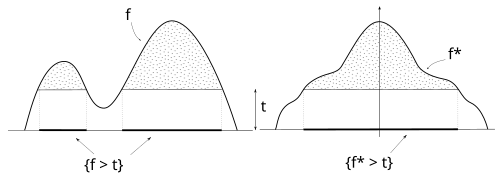
関数とその対称的な減少の再配置により、レベル セットの測定が保存されます。

この関数は対称な減少関数であり、そのレベルセットは のレベルセットと同じ測度を持ち、 ${\displaystyle f^{*}}$ ${\displaystyle f,}$ $${\displaystyle |\{x:f^{*}(x)>t\}|=|\{x:f(x)>t\}|.}$$

が関数である 場合${\displaystyle f}$ ${\displaystyle L^{p},}$ $${\displaystyle \|f\|_{L^{p}}=\|f^{*}\|_{L^{p}}.}$$

ハーディ・リトルウッド不等式は成り立ち、 $${\displaystyle \int fg\leq \int f^{*}g^{*}.}$$

さらに、ポリア・シェゲー不等式が成り立つ。これは、もし、そしてならば、 ${\displaystyle 1\leq p<\infty }$ ${\displaystyle f\in W^{1,p}}$ $${\displaystyle \|\nabla f^{*}\|_{p}\leq \|\nabla f\|_{p}.}$$

対称的な減少再配置は順序を保存し、距離を減少させる。つまり 、 ${\displaystyle L^{p}}$ $${\displaystyle f\leq g{\text{ implies }}f^{*}\leq g^{*}}$$ $${\displaystyle \|f-g\|_{L^{p}}\geq \|f^{*}-g^{*}\|_{L^{p}}.}$$

アプリケーション

ポリア・シェゲー不等式は、極限の場合、等周不等式 を生じます。また、調和関数とのいくつかの関係を用いて、レイリー・ファーバー・クラーン不等式 を証明することもできます。 ${\displaystyle p=1,}$

非対称減少転位

を、すべての非負の実数上の関数として定義することもできます。^[2]をσ 有限測度空間とし 、を有限（つまり、実数）値μ-aeのみを取る測定可能な関数とします（ただし、「-ae」は、-測度ゼロの集合を除く可能性があることを意味します）。分布関数を規則によって 定義します。これで、の減少並べ替え（または、場合によっては非増加並べ替え）を規則によって 関数として 定義できます。 このバージョンの減少並べ替えは非負の実数上でのみ定義されているため、対称ではないことに注意してください。ただし、対称バージョンとして上記に挙げたのと同じプロパティの多くを継承します。 ${\displaystyle f^{*}}$ ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle (E,\mu )}$ ${\displaystyle f:E\to [-\infty ,\infty ]}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle \mu _{f}:[0,\infty ]\to [0,\infty ]}$ $${\displaystyle \mu _{f}(s)=\mu \{x\in E:\vert f(x)\vert >s\}.}$$ ${\displaystyle f}$ ${\displaystyle f^{*}:[0,\infty )\to [0,\infty ]}$ $${\displaystyle f^{*}(t)=\inf\{s\in [0,\infty ]:\mu _{f}(s)\leq t\}.}$$

• ${\displaystyle f}$ およびは等測定可能であり、つまり同じ分布関数を持ちます。${\displaystyle f^{*}}$
• ハーディ・リトルウッド不等式は成り立ち、${\displaystyle \int _{E}|fg|\;d\mu \leq \int _{0}^{\infty }f^{*}(t)g^{*}(t)\;dt.}$
• ${\displaystyle \vert f\vert \leq \vert g\vert }$ ${\displaystyle \mu }$ -aeは${\displaystyle f^{*}\leq g^{*}.}$
• ${\displaystyle (af)^{*}=|a|f^{*}}$ すべての実数について${\displaystyle a.}$
• ${\displaystyle (f+g)^{*}(t_{1}+t_{2})\leq f^{*}(t_{1})+g^{*}(t_{2})}$ すべての人のために${\displaystyle t_{1},t_{2}\in [0,\infty ).}$
• ${\displaystyle |f_{n}|\uparrow |f|}$ ${\displaystyle \mu }$ -aeは${\displaystyle f_{n}^{*}\uparrow f^{*}.}$
• ${\displaystyle \left(\vert f\vert ^{p}\right)^{*}=(f^{*})^{p}}$ すべての正の実数に対して${\displaystyle p.}$
• ${\displaystyle \|f\|_{L_{p}(E)}=\|f^{*}\|_{L_{p}[0,\infty )}}$ すべての正の実数に対して${\displaystyle p.}$
• ${\displaystyle \|f\|_{L_{\infty }(E)}=f^{*}(0).}$

（非対称）減少再配置関数は、再配置不変なバナッハ関数空間の理論において頻繁に登場する。特に重要なのは以下の点である。

ルクセンブルグの表現定理。共鳴測度空間上の再配置不変なバナッハ関数ノルムを とすると、 有限値-aeであるすべての非負可測関数に対してとなるような（おそらく一意ではない）再配置不変な関数ノルムが存在する。${\displaystyle \rho }$ ${\displaystyle (E,\mu ).}$ ${\displaystyle {\overline {\rho }}}$ ${\displaystyle [0,\infty )}$ ${\displaystyle \rho (f)={\overline {\rho }}(f^{*})}$ ${\displaystyle f:E\to [0,\infty ]}$ ${\displaystyle \mu }$

上記の定理のすべての用語（つまり、バナッハ関数ノルム、再配置不変バナッハ関数空間、共鳴測度空間）の定義は、Bennett と Sharpley の本のセクション 1 と 2 に記載されていることに注意してください（以下の参考文献を参照）。

参照

• 等周不等式 – 任意の閉曲線に適用可能な幾何学的不等式
• レイヤーケーキの表現 – 数学における概念
• レイリー・ファーバー・クラーン不等式 – 幾何波動現象
• リース転位不等式
• ソボレフ空間 – 数学における関数のベクトル空間
• セゲー不等式 – 数学的解析における概念Pages displaying short descriptions of redirect targets

参考文献

1. リーブ、エリオット、ロス、マイケル(2001).解析. 大学院数学研究科. 第14巻 (第2版).アメリカ数学会. ISBN 978-0821827833。
2. ベネット、コリン、シャープリー、ロバート (1988).演算子の補間. ISBN 978-0-120-88730-9。