3ギャップ定理

円上の点間の距離について

数学において、三ギャップ定理、三距離定理、あるいはシュタインハウス予想とは、円上にn個の点を、開始点からθ、2 θ、3 θ 、… の角度で配置した場合、円周上の隣接する位置にある点のペア間の距離は最大で 3 つしかないというものである。距離が 3 つある場合、そのうち最大の距離は常に他の 2 つの距離の合計に等しい。[1] θがπの有理倍でない限り、少なくとも 2 つの異なる距離が存在する。

この結果はヒューゴ・シュタインハウスによって予想され、1950年代にヴェラ・T・ソス、ヤーノシュ・スラーニ [hu]、スタニスワフ・シフィエルチコフスキによって証明されました。その後、他の人々によってさらなる証明が加えられました。三ギャップ定理の応用としては、植物の成長や音楽の調律システムの研究、鏡面反射された正方形内での光の反射理論などがあります。

声明

三ギャップ定理は、円上の点を用いて幾何学的に述べることができる。この形では、円上に点を始点から の角度で配置した場合、円周上の隣接する位置にある点のペア間の距離は最大で 3 つになる、と述べている。これと同等でより代数的な形は、実数の倍数の小数部に関するものである。これは、任意の正の実数と整数について、数の小数部が単位区間を最大で 3 つの異なる長さの部分区間に分割することを述べている。この 2 つの問題は、単位区間と円周との線形対応、および実数と角度との対応のもとで同等である。[2] [3] [4] n {\displaystyle n} θ 、 2 θ 、 … 、 n θ {\displaystyle \theta ,2\theta ,\dots ,n\theta } α {\displaystyle \alpha} n {\displaystyle n} α 、 2 α 、 … 、 n α {\displaystyle \alpha,2\alpha,\dots,n\alpha} α {\displaystyle \alpha} θ ＝ 2 π α {\displaystyle \theta =2\pi \alpha }

アプリケーション

植物の成長

連続する葉が黄金角によって区切られている植物の茎の端面図

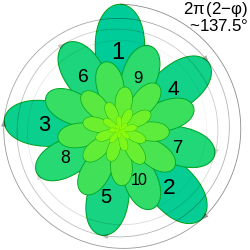
植物の茎における葉の配置である葉序の研究では、多くの植物の茎において、後続の葉が前の葉に対して黄金角（約137.5°）だけ回転していることが観察されています。この角度は、植物の葉が太陽光を集める力を最大化すると考えられています。[5]このように成長した植物の茎を真横から見ると、この真横から見たときの周期的な順序で連続する2枚の葉の間には、最大で3つの異なる角度が見られます。[6]

フェルマー螺旋(中央)に沿った黄金角で間隔をあけられた点は、他の角度の場合よりも均一に間隔をあけられています。

たとえば、図では、これら 3 つの角度のうち最大の角度は、葉 3 と 6 の間、葉 4 と 7 の間、葉 5 と 8 の間に 3 回出現しています。2 番目に大きな角度は、葉 6 と 1 の間、葉 9 と 4 の間、葉 7 と 2 の間、葉 10 と 5 の間、葉 8 と 3 の間に 5 回出現しています。また、最小の角度は、葉 1 と 9 の間、葉 2 と 10 の間の 2 回だけ出現しています。3 種類の異なる隙間があるという現象は、成長パターンが一定の回転角度を使用するという事実のみに依存しており、この角度と黄金比の関係には依存していません。同じ現象は、黄金比だけでなく、他のどの回転角度でも発生します。ただし、この成長パターンの他の特性は黄金比に依存しています。たとえば、黄金比が近似しにくい数であるという事実は、フェルマーの螺旋に沿ってこの角度で間隔を空けられた点(植物の成長のいくつかのモデルのように) がDelone 集合を形成することを意味します。直感的に言えば、これはそれらが均等に間隔をあけられていることを意味します。[7]

音楽理論

ピタゴラス音律の音を半音円の点として表す。辺は音律を構成する完全五度を示す。連続する点の間の2つの長い間隔は半音を表し、十二音円が閉じない短い間隔はピタゴラスコンマである。

音楽理論では、音程は2 つの楽音間の周波数の比率を表します。音程は、2 つの小さな整数の比率である場合に一般的に協和または調和的であると見なされます。たとえば、オクターブは比率 2:1 に対応し、完全五度は比率 3:2 に対応します。[8] 2 つの音は、オクターブの整数だけ異なる場合に一般的に同等であると見なされます。この同等性は、半音円で幾何学的に表すことができます。半音円の点は同等の音のクラスを表します。数学的には、この円は複素平面内の単位円として記述でき、特定の音を表すこの円上の点は、周波数を複素数にマッピングすることで取得できます。比率のある音程は、この円上の点の間の角度に対応します。つまり、2 つの楽音は、円上の 2 つの点がこの角度だけ異なるときに、特定の音程だけ異なります。たとえば、次の式では、オクターブに対応する角度として (全円) が得られます。 3/2は2の有理数乗ではないので、完全5度を表す半音円上の角度は の有理数倍ではなく、同様にオクターブ以外の一般的な音楽音程は有理数角に対応しません。[9] ν {\displaystyle \nu} 経験 ⁡ （ 2 π 私 ログ 2 ⁡ ν ） {\textstyle \exp(2\pi i\log _{2}\nu )} ρ {\displaystyle \rho } 2 π ログ 2 ⁡ ρ {\displaystyle 2\pi \log _{2}\rho } 2 π {\displaystyle 2\pi } 2 π {\displaystyle 2\pi }

調律システムとは、音楽の作曲や演奏に使われる音の集まりです。例えば、ピアノで一般的に使われる平均律は、半音円上に等間隔に配置された 12 の音からなる調律システムです。他の調律システムでは、音を等間隔に配置しず、特定の音程の連続する倍数として音を生成します。その一例がピタゴラス音律で、これはこのようにして 5 度圏で完全 5 度の連続する倍数として生成される 12 の音から構成されます。半音円上で完全 5 度が作る無理角は円の 7/12 に近いため、ピタゴラス音律の 12 の音は、同じように円のちょうど 7/12 の角度を使用して生成できる平均律の 12 の音に近いですが、同じではありません。[10]平均律の音はちょうど円の1/12の角度で間隔が空けられていますが、ピタゴラス音律の音は、円の1/12に近いけれども正確には円の1/12ではない2つの異なる角度の音程で区切られており、2つの異なるタイプの半音を表しています。[11]ピタゴラス音律をさらに完全5度拡張して13音にすると、その音の間の音程のシーケンスには、3番目のはるかに短い音程、ピタゴラスコンマが含まれます。[12]

この文脈において、三間隙定理は、このようにして単一の音程の連続する倍数によって生成されるあらゆる調律体系を記述するために用いることができる。これらの調律体系の中には（平均律のように）、最も近い音のペアを隔てる音程が1つしかないものもあれば、（ピタゴラス音律のように）音を隔てる音程が2つしかないものもあるが、三間隙定理は、音を隔てる音程は常に最大で3つであることを意味する。[13] [14]

鏡面反射

フィボナッチ語 （スターム語の例）には、長さ 3 の部分列が 4 つあります（左から右の順）：010、100、001、101。

シュトゥルム語とは、無理数傾きの直線に沿って始まる、鏡面正方形内の光線の水平反射と垂直反射の列を表す2つの記号（例えば「H」と「V」）の無限列である。同様に、同じ列は、開始線が交差する整数グリッドの水平線と垂直線の列を表す。このような列に共通する特性の1つは、任意の正の整数nに対して、長さnの連続する部分列が正確にn + 1個存在することである。各部分列は特定の頻度で無限に出現し、3ギャップ定理によれば、これらのn + 1個の部分列は最大で3つの異なる頻度で出現する。頻度が3つある場合、最大の頻度は他の2つの頻度の合計と等しくなければならない。この結果の証明の一つは、開始ラインのy切片（法1）を、シーケンスの最初のn要素が同じであるn + 1個のサブインターバルに分割し、この分割に3ギャップ定理を適用することである。[15] [16]

歴史と証明

3ギャップ定理はヒューゴ・シュタインハウスにより予想され、その最初の[17]証明は1950年代後半にヴェラ・T・ソス[18]、ヤノシュ・スラーニ [hu]、[19]、スタニスワフ・シフィエルチコフスキ[20]によりなされました。その後の研究者らは追加の証明を発表し、[21]この結果を高次元に一般化し[22] [23] [24] [25]、連分数[ 4 ] [26] 、リーマン多様体の対称性と測地線[27]、エルゴード理論[28]、平面格子の空間[3]などのトピックに関連付けました。Mayero (2000)はRocq（当時はCoq）対話型定理証明器を使用して証明を形式化しました。[2]

次の簡単な証明は、Frank Liang によるものです。θ を、円上の θ の連続する倍数として点の集合を生成する回転角とします。ギャップを、与えられた集合の 2 つの隣接する点の間に延びる円弧 A と定義し、ギャップの端点が、 θの倍数のシーケンスの中で、他の同じ長さのギャップよりも後に現れる場合、そのギャップは固定ギャップであると定義します。この定義から、すべてのギャップは固定ギャップと同じ長さであることがわかります。 A が固定ギャップである場合、A + θはギャップではありません。なぜなら、同じ長さであり、1 ステップ後になるからです。これが発生する唯一の方法は、Aの端点の 1 つがθの倍数のシーケンスの最後の点になるか(つまり、A + θの対応する端点がない)、指定された点の 1 つがA + θ内にあり、ギャップにならないことです。ある点がA + θ内に収まるのは、それがθの倍数の列の最初の点である場合のみです。そうでなければ、その前の点がA内に収まるため、 Aがギャップであるという仮定に矛盾します。したがって、固定ギャップは最大で3つ、つまり最後の点の両側に2つ、そして最初の点（もしそれが列の一部であったとしたら）の前の点が収まる1つのギャップが存在することになります。固定ギャップは最大で3つなので、ギャップの長さも最大で3つになります。[29] [30]

リャンの証明はさらに、ギャップ長がちょうど3つある場合、最長のギャップ長は他の2つのギャップ長の合計となることを示している。なぜなら、この場合、最初の点を含む回転コピーA + θは、その点によって2つの小さなギャップに分割され、それが他の2つのギャップとなるからである。 [29] [30]リャンはより一般的な結果である「距離定理」も証明している。これによれば、円周上の異なる等差数列の和は、最大で異なるギャップ長を持つ。[29] 3ギャップ定理において、 θ /2 πが近似困難な数である場合に限り、3つのギャップ間の比には一定の上限が存在する。[7] 3 d {\displaystyle 3d} d {\displaystyle d} 3 d {\displaystyle 3d}

密接に関連しているが、より古い定理として「三ギャップ定理」とも呼ばれるものがあり、Aが任意の円弧である場合、Aに含まれるθの倍数の整数列は、列の値の間に最大3つのギャップの長さを持つというものである。繰り返しになるが、ギャップの長さが3つある場合、そのうちの1つは他の2つのギャップの長さの和である。[31] [32]

参照

参考文献

  1. ^ Allouche, Jean-Paul; Shallit, Jeffrey (2003)、「2.6 3距離定理」、Automatic Sequences: Theory, Applications, Generalizations、ケンブリッジ大学出版局、pp.  53– 55、ISBN 9780521823326
  2. ^ ab Mayero, Micaela (2000), 「3ギャップ定理（シュタインハウス予想）」, Types for Proofs and Programs: International Workshop, TYPES'99, Lökeberg, Sweden, June 12–16, 1999, Selected Papers , Lecture Notes in Computer Science, vol. 1956, Springer, pp.  162– 173, arXiv : cs/0609124 , doi :10.1007/3-540-44557-9_10, ISBN 978-3-540-41517-6、S2CID  3228597
  3. ^ ab Marklof, Jens; Strömbergsson, Andreas (2017)、「3ギャップ定理と格子空間」、アメリカ数学月刊誌、124 (8): 741– 745、arXiv : 1612.04906、doi :10.4169/amer.math.monthly.124.8.741、hdl :1983/b5fd0feb-e42d-48e9-94d8-334b8dc24505、JSTOR  10.4169/amer.math.monthly.124.8.741、MR  3706822、S2CID  119670663
  4. ^ ab van Ravenstein, Tony (1988)、「3ギャップ定理（シュタインハウス予想）」、オーストラリア数学会誌、シリーズA、45 (3): 360– 370、doi : 10.1017/S1446788700031062、MR  0957201
  5. ^ アダム、ジョン・A.（2011）、数学的自然散策、プリンストン大学出版、  pp.35-41、ISBN 9781400832903
  6. ^ van Ravenstein, Tony (1987)、「数列と葉序」、オーストラリア数学会報、36 (2): 333、doi : 10.1017/s0004972700026605
  7. ^ ab 秋山 茂樹 (2020年3月)、「スパイラルデローン集合と3距離定理」、非線形性、33 (5): 2533– 2540、arXiv : 1904.10815、Bibcode :2020Nonli..33.2533A、doi :10.1088/1361-6544/ab74ad、S2CID  129945118
  8. ^ Haack, Joel K. (1999)、「テリー・ライリーの音楽に用いられる純正律の数学」、Sarhangi, Reza (編)、『Bridges: Mathematical Connections in Art, Music, and Science』、サウスウェスタン大学、ウィンフィールド、カンザス州: Bridges Conference、pp.  101– 110、ISBN 0-9665201-1-4
  9. ^ Baroin, Gilles; Calvet, André (2019)、「Visualizing temperaments: squaring the circle?」、Montiel, Mariana; Gomez-Martin, Francisco; Agustín-Aquino, Octavio A. (eds.), Mathematics and Computation in Music: 7th International Conference, MCM 2019, Madrid, Spain, June 18–21, 2019, Proceedings , Lecture Notes in Computer Science, vol. 11502, Springer International Publishing, pp.  333– 337, doi :10.1007/978-3-030-21392-3_27, ISBN 978-3-030-21391-6、S2CID  184482714
  10. ^ ケアリー、ノーマン; クランプリット、デイヴィッド (1989年10月)、「整形式スケールの側面」、ミュージック・セオリー・スペクトラム、11 (2): 187– 206、doi :10.2307/745935、JSTOR  745935
  11. ^ Strohm, Reinhard; Blackburn, Bonnie J.編 (2001) 『中世後期における音楽の概念と実践』第3巻第1部、新オックスフォード音楽史、オックスフォード大学出版局、252ページ、ISBN 9780198162056
  12. ^ ベンソン、ドナルド・C.（2003）、A Smoother Pebble：数学的探究、オックスフォード大学出版局、p.51、ISBN 9780198032977
  13. ^ ケアリー、ノーマン（2007）「整形式音階と対整形式音階における一貫性と同一性」、数学と音楽ジャーナル、1（2）：79-98、doi：10.1080/17459730701376743、S2CID  120586231
  14. ^ 成島照美（2017）「微分音とアーヴ・ウィルソンの調律システム：倍音スペクトルのマッピング」ラウトレッジ音楽理論研究、ラウトレッジ、  90～ 91頁、ISBN 9781317513421
  15. ^ ロテール、M. (2002)、「スターム語」、語の代数的組合せ論、ケンブリッジ：ケンブリッジ大学出版局、pp.  40– 97、ISBN 978-0-521-81220-7、Zbl  1001.68093ロテールは、単語の長さが一定であるという性質を、定義の帰結としてではなく、シュトゥルム語の定義として用いている。この性質とここで述べた定義の同値性については、定理2.1.13（p. 51）を参照のこと。これらの単語の3つの頻度については、定理2.2.37（p. 73）を参照のこと。 d + 1 {\displaystyle d+1} d {\displaystyle d}
  16. ^ アレッサンドリ、パスカル; Berthé、Valérie (1998)、「単語に関する 3 つの距離定理と組み合わせ論」、L'Enseignement mathématique、44 ( 1–2 ): 103–132、MR  1643286特にセクション2.1「回転の符号化の複雑さと頻度」を参照
  17. ^ ヘインズ、アラン; Marklof、Jens (2020)、「均一ダイナミクスによる高次元の Steinhaus および Slater 問題」、高等師範科学誌、53 (2): 537–557、arXiv : 1707.04094、doi :10.24033/asens.2427、MR  4094564、S2CID  67851217、この驚くべき事実の最初の証明は、1957 年に Sós によって、1958 年に Surányi によって、そして 1959 年に Świerczkowski によって出版されました。
  18. ^ Sós, VT (1958), 「数列の分布 mod 1 について」, Ann. Univ. Sci. Budapest, Eötvös Sect. Math. , 1 : 127– 134 n α {\displaystyle n\alpha }
  19. ^ Surányi、J. (1958)、「Über die Anordnung der Vielfachen einer reelen Zahl mod 1」、Ann.大学科学。ブダペスト、エトヴェシュ支部数学。、1：107～ 111
  20. ^ Świerczkowski, S. (1959)、「円周上の円弧の連続設定について」、Fundamenta Mathematicae、46 (2): 187–189、doi : 10.4064/fm-46-2-187-189、MR  0104651
  21. ^ これらの証明は Marklof & Strömbergsson (2017) によって簡単に調査および分類されており、以下の証明の分類とその多くの参照はそこから引用されています。
  22. ^ ハルトン、ジョン・H.（1965）、「数列の分布」、ケンブリッジ哲学協会数学紀要、61（3）：665-670、doi：10.1017/S0305004100039013、MR  0202668、S2CID  123400321 { n ξ } （ n ＝ 0 、 1 、 2 、 … ） {\displaystyle \{n\xi \}\,(n=0,\,1,\,2,\,\ldots )}
  23. ^ シュヴァリエ、ニコラス（2007）、「巡回群と3距離定理」、カナダ数学ジャーナル、59（3）：503–552、doi：10.4153 / CJM-2007-022-3、MR  2319157、S2CID  123011205
  24. ^ Vijay, Sujith (2008)、「ユークリッド距離は11個あれば十分」、Journal of Number Theory、128 (6): 1655– 1661、arXiv : math/0609536、doi : 10.1016/j.jnt.2007.08.016、MR  2419185、S2CID  119655772
  25. ^ Bleher, Pavel M.; Homma, Youkow; Ji, Lyndon L.; Roeder, Roland KW; Shen, Jeffrey D. (2012)「円周上の最近傍距離：多次元の場合」、Journal of Statistical Physics、146 (2): 446– 465、arXiv : 1107.4134、Bibcode :2012JSP...146..446B、doi :10.1007/s10955-011-0367-8、MR  2873022、S2CID  99723
  26. ^ スレーター、ノエル・B. (1967)、「シーケンスのギャップとステップ」、ケンブリッジ哲学協会数学紀要、63 (4): 1115– 1123、doi :10.1017/S0305004100042195、MR  0217019、S2CID  121496726 n θ モッド 1 {\displaystyle n\theta {\bmod {1}}}
  27. ^ イアン・ビリンジャー; Schmidt、Benjamin (2008)、「3 つのギャップ定理とリーマン幾何学」、Geometriae Dedicata、136 : 175–190、arXiv : 0803.1250、doi :10.1007/s10711-008-9283-8、MR  2443351、S2CID  6389675
  28. ^ Haynes, Alan; Koivusalo, Henna ; Walton, James; Sadun, Lorenzo (2016)、「カットセットと射影セットにおけるパッチのギャップ問題と頻度」(PDF)、ケンブリッジ哲学協会数学紀要、161 (1): 65– 85、Bibcode :2016MPCPS.161...65H、doi :10.1017/S0305004116000128、MR  3505670、S2CID  55686324
  29. ^ abc Liang, Fr​​ank M. (1979)、「距離定理の簡潔な証明」、離散数学、28 (3): 325– 326、doi : 10.1016/0012-365X(79)90140-7、MR  0548632 3 d {\displaystyle 3d}
  30. ^ ab Shiu, Peter (2018)、「3ギャップ定理への脚注」、アメリカ数学月刊誌、125 (3): 264– 266、doi :10.1080/00029890.2018.1412210、MR  3768035、S2CID  125810745
  31. ^ Slater, NB (1950)、「 整数の分布」、ケンブリッジ哲学協会数学紀要、46 (4): 525– 534、doi :10.1017/S0305004100026086、MR  0041891、S2CID  120454265 北 {\displaystyle N} θ 北 < ϕ {\displaystyle \theta N<\phi }
  32. ^ Florek, K. ( 1951)、「Une remarque sur la répartition des nombres 」、Colloquium Mathematicum、2 : 323–324 n ξ （ モッド ⁡ 1 ） {\displaystyle n\xi \,(\operatorname {mod} 1)}
「https://en.wikipedia.org/w/index.php?title=Three-gap_theorem&oldid=1311884606」より取得