原始ピタゴラス数列の樹形図

整数直角三角形の数学的木

原始ピタゴラス数列の樹木とは、各ノードが原始ピタゴラス数列を表し、各原始ピタゴラス数列が正確に1つのノードで表される数学的な樹木です。このような樹木のうち、バーグレンの樹木とプライスの樹木では、樹木の根は $(3, 4, 5)の数列であり、各ノードは$ 線形変換によって生成された正確に3つの子を持ちます。

ピタゴラス数列は、3つの正の整数 $a$ 、 $b$ 、 $c$ の集合であり、それぞれ直角三角形の2辺と斜辺になることができるという性質を持ち、したがって方程式を満たす。この数列は、 $a$ 、 $b$ 、 $c$ の最大公約数が1である場合にのみ原始的であると言われる。原始ピタゴラス数列では、 $a$ 、 $b$ 、 $cは$ 互いに素でもある。すべての原始ピタゴラス数列の集合は、自然な形で根付き木、具体的には3分木の構造を持つ。これは1934年にB. Berggrenによって初めて発見された。^[1] $a^{2}+b^{2}=c^{2}$

FJMバーニングは^{[2] 、3つの}行列のいずれかが

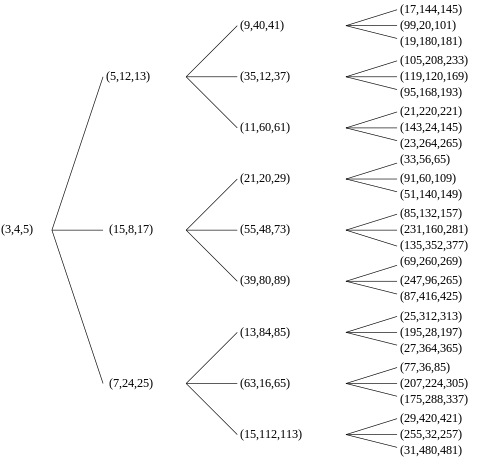
{\begin{array}{lcr}A={\begin{bmatrix}1&-2&2\\2&-1&2\\2&-2&3\end{bmatrix}}&B={\begin{bmatrix}1&2&2\\2&1&2\\2&2&3\end{bmatrix}}&C={\begin{bmatrix}-1&2&2\\-2&1&2\\-2&2&3\end{bmatrix}}\end{array}}

の右側に、ピタゴラス数列を形成する列ベクトルを乗じると、結果は、異なるピタゴラス数列を成分とする別の列ベクトルになります。最初の数列が原始数列であれば、結果の数列も原始数列です。したがって、各原始ピタゴラス数列には 3 つの「子」があります。すべての原始ピタゴラス数列は、このようにして数列 $(3, 4, 5)$ から派生し、同じ原始数列が複数回出現することはありません。結果は、ルートノードに $(3, 4, 5)$ がある無限三分木としてグラフィカルに表現できます(右側の典型的な木を参照)。この木は、1970 年の A. Hall ^[3]と 1990 年の AR Kanga ^{[4]の論文にも登場しました。2008 年に VE Firstov は、このような三分木は 3 つしか存在せず、Berggren のツリーに似ていますが、最初のノード} $(4, 3, 5)$ から始まるツリーを明示的に与えることを一般化しました。^[5]

証明

完全に原始的なピタゴラス数列の存在

$最初のノードに(3, 4, 5)$ が存在するような原始ピタゴラス数列から始めて、生成される各数列がピタゴラス数列と原始数列の両方であることを示すことにより、ツリーに原始ピタゴラス数列しか含まれず、それ以外は何も含まれていないことが帰納的に示されます。

ピタゴラスの性質の保存

上記のいずれかの行列、たとえば $A を$ 、ピタゴラスの性質 $a$ $2$ $+$ $b$ $2$ $=$ $c$ $2$ を持つ3 つ組 $(a, b, c) T$ に適用して新しい 3 つ組 $($ $d$ $,$ $e$ $,$ $f$ $)$ $T$ $=$ $A$ $($ $a$ $,$ $b$ $,$ $c$ $)$ $T$ を取得した場合、この新しい 3 つ組もピタゴラスの性質を持ちます。これは、 $d$ 、 $e$ 、 $fをそれぞれ$ $a$ 、 $b$ 、 $c$ の 3 つの項の合計として書き出し、それぞれを 2乗し、 $c$ $2$ $=$ $a$ $2$ $+$ $b$ $2を代入して$ $f$ $2$ $=$ $d$ $2$ $+$ $e$ $2$ を取得することで確認できます。これは $Aだけでなく、$ $B$ と $C$ にも当てはまります。

原始性の保存

行列 $A$ 、 $B$ 、 $C$ はすべてユニモジュラです。つまり、整数要素のみを持ち、行列式は ±1 です。したがって、その逆行列もユニモジュラであり、特に整数要素のみを持ちます。そのため、それらのいずれか、たとえば $A$ を原始ピタゴラス数列 $(a 、 b 、 c) T$ $に適用して別の数列(d 、 e 、 f) T$ を取得すると、 $(d 、 e 、 f) T = A (a 、 b 、 c) T$ となり、したがって $(a 、 b 、 c) T = A -1 (d 、 e 、 f) T$ $となります。 d$ 、 $e$ 、 $f$ のうちの任意の 2 つ (したがって 3 つすべて) が任意の素因数を共有している場合、この最後の式により、その素因数は $a$ 、 $b$ 、 $c$ のそれぞれも割り切れます。したがって、 $a$ 、 $b$ 、 $c が$ 互いに素であるならば、 $d$ 、 $e$ 、 $f$ も互いに素でなければなりません。これは $A$ だけでなく、 $B$ と $C$ にも当てはまります。

あらゆる原始ピタゴラス数列が正確に1回ずつ存在する

木にはあらゆる原始ピタゴラス数列が 1 つしか含まれないことを示すには、そのような数列に対して、木を通って開始ノード $(3, 4, 5)$ に戻る経路が 1 つだけ存在することを示せば十分です。これは、ユニモジュラー逆行列 $A -1$ 、 $B -1$ 、 $C -1$ をそれぞれ任意の原始ピタゴラス数列 $(d 、 e 、 f)に適用することで確認できます。上記の推論により原始性とピタゴラスの性質が保持され、$ $(3, 4, 5)$ より大きい数列に対しては、逆遷移行列の 1 つが、すべて正の要素 (およびより小さい斜辺) を持つ新しい数列を生成することに注意してください。帰納法により、この新しい有効な数列自体から、より小さい有効な数列が 1 つ生成され、これが続きます。潜在的な斜辺がどんどん小さくなるという有限性により、最終的に $(3, 4, 5) に$ 到達します。これは、ステップを逆にすることで $(3, 4, 5)から到達できるため、$ $(d, e, f)$ が実際にツリー内に出現することを証明しています。また、 $($ $d$ $,$ $e$ $,$ $f$ $)から$ $(3, 4, 5)$ へのパスは 1 つしかないため、一意に出現します。

プロパティ

$行列A$ を使用した変換を $(a 、 b 、 c) = (3、 4、 5)$ から繰り返し実行すると、特徴 $b + 1 = c$ が保持されます。行列 $Bは$ $(3、 4、 5)$ から $a - b = \pm1$ を保持し、行列 $Cは$ $(3、 4、 5)$ から $a$ $+ 2 =$ $c$ の特徴を保持します。

この樹形の幾何学的解釈は、各ノードに存在する外接円に関係する。任意の親三角形の3つの子三角形は、親三角形から内接円の半径を「継承」する。つまり、親三角形の外接円の半径が次の世代の内接円の半径となる。^[6]^{: p.7} 例えば、親三角形 $(3, 4, 5)の外接円の半径はそれぞれ2、3、6である。これらは、3つの子三角形$ $(5, 12, 13)$ 、 $(15, 8, 17)$ 、 $(21, 20, 29)$ の内接円の半径と正確に一致する。

初期条件として使用される任意のピタゴラスの三つ組から $A$ または $C$ のいずれかを繰り返し適用すると、 $a$ 、 $b$ 、 $c$ のいずれかのダイナミクスは、 $x$ のダイナミクスとして表現できます。

x_{n+3}-3x_{n+2}+3x_{n+1}-x_{n}=0\,

これは行列の共通特性方程式に基づいている

\lambda^{3}-3\lambda^{2}+3\lambda-1=0.\,

$B$ を繰り返し適用すると、 $a$ 、 $b$ 、 $c$ のいずれかのダイナミクスは $x$ のダイナミクスとして表現できます。

x_{n+3}-5x_{n+2}-5x_{n+1}+x_{n}=0,\,

$これはB$ の特性方程式を模倣したものである。^[7]

さらに、3つの行列のいずれかを任意の回数、任意の順序で掛け合わせることで、無数の3階単変数差分方程式を見つけることができます。例えば、行列 $D = CB は$ 、1ステップでツリーから2ノード（横に、次に下に）移動します。D の特性方程式は、 $Dによって形成される非$ $網羅$ 的なツリー内の $a$ 、 $b$ 、または $c$ のいずれかの3階ダイナミクスのパターンを提供します。

ツリーを生成する代替方法

2つのパラメータを使用する

この木のダイナミクスに対する別のアプローチ^[8]は、すべての原始ピタゴラス数列を生成するための標準的な公式に依存しています。

a=m^{2}-n^{2},\,

b=2mn,\,

c=m^{2}+n^{2},\,

ただし、 $m > n > 0$ かつ $m$ と $n は$ 互いに素で、かつ奇偶性が逆である（つまり、両方が奇数ではない）。ペア $(m, n)$ は、列ベクトルとして表現されるものを以下のいずれかの式で前置して乗算することで反復処理できる。

{\begin{array}{lcr}{\begin{bmatrix}2&-1\\1&0\end{bmatrix}},&{\begin{bmatrix}2&1\\1&0\end{bmatrix}},&{\begin{bmatrix}1&2\\0&1\end{bmatrix}},\end{array}}

それぞれの木は不等式、互いに素であること、そして逆偶奇性を保持します。結果として得られる三分木は、 $(2, 1)から始まり、そのような$ $(m, n)$ のペアをすべて1つずつ含み、 $(a, b, c)$ の三つ組に変換すると、上記の木と同一になります。

あるいは、ルートノードを $(m, n)=(3,1)から始めることもできます。$ ^[9]すると $、$ 行列の乗算で不等式と互いに素な関係が保たれ、 $m$ と $nはどちらも奇数のままです。対応する原始ピタゴラス数列は$ $、$ $a = (m2 - n2)/2$ 、 $b = mn$ 、 $c = (m2 + n2)/2$ となります。この木は、 $a$ と $b$ $が$ $入れ替わっただけの$ 同じ原始ピタゴラス数列を生成します。

1つのパラメータを使用する

このアプローチは、半角のタンジェントから任意の原始ピタゴラス数列を生成するための標準的な公式に依存しています。具体的には、 $t = n / m = b / (a + c)$ と記述します。ここで、 $tは長さ$ $b$ の辺と反対側の内角の半分のタンジェントです。ツリーのルートノードは $t$ $= 1/2$ で、これは原始ピタゴラス数列 $(3, 4, 5)のノードです。値が$ $t$ であるノードの場合、その 3 つの子は $1 / (2 -$ $t$ $)$ 、 $1 / (2 +$ $t$ $)$ 、および $t$ $/ (1 + 2$ $t$ $)です。このような値$ $t$ に関連付けられた原始ピタゴラス数列を見つけるには、 $(1 -$ $t$ $2$ $、 2$ $t$ $、 1 +$ $t$ $2$ $)$ を計算し、3 つの値すべてにその分母の最小公倍数を掛けます。 (あるいは、 $t$ $=$ $n$ $/$ $m を$ 最小の分数として書き、前のセクションの式を使用します。) 代わりに $t$ $= 1/3 の値を持つルートノードは、$ $a$ と $b$ の値が入れ替わった、同じ基本ピタゴラス数列のツリーを生成します。

別の木

あるいは、プライスが発見した3つの異なる行列を使うこともできる。^[6]

{\begin{array}{lcr}A'={\begin{bmatrix}2&1&-1\\-2&2&2\\-2&1&3\end{bmatrix}}\,,&B'={\begin{bmatrix}2&1&1\\2&-2&2\\2&-1&3\end{bmatrix}}\,,&C'={\begin{bmatrix}2&-1&1\\2&2&2\\2&1&3\end{bmatrix}}\,.\end{array}}

$セット{A 、 B 、 C}$ によって生成される 3 つの子と、セット ${A' 、 B' 、 C'}$ によって生成される子は同じではありませんが、各セットはすべての基本トリプルを個別に生成します。

たとえば、 $[5, 12, 13]を$ 親として使用すると、3つの子のセットが2つ得られます。

{\begin{array}{ccc}&\left[5,12,13\right]&\\A&B&C\\\left[45,28,53\right]&\left[55,48,73\right]&\left[7,24,25\right]\end{array}}\quad \quad \quad \quad \quad {\begin{array}{ccc}{}&\left[5,12,13\right]&{}\\A'&B'&C'\\\left[9,40,41\right]&\left[35,12,37\right]&\left[11,60,61\right]\end{array}}

注釈と参考文献

^ B. Berggren、「Pytagoreiska trianglar」（スウェーデン語）、Elementa: Tidskrift för elementär matematik、fysik och kemi 17 (1934)、129–139。根付き木については6ページをご覧ください。
^ Barning、FJM (1963)、「Over pythagorese en bijna-pythagorese driehoeken en een Generatieprocesmet behulp van unimodulaire matrices」(オランダ語)、Math.セントラムアムステルダム空軍ズイベレウィスク。 ZW-011: 37、https://ir.cwi.nl/pub/7151
^ A. Hall、「ピタゴラスの三つ組の系譜」、The Mathematical Gazette、第54巻、第390号、1970年12月、377～379ページ。
^ Kanga, AR、「ピタゴラスの三つ組の家系図」『数学とその応用研究所紀要』 26、1990年1月/2月、15-17ページ。
^ Firstov, VE (2008). 「原始対の特殊行列変換半群とピタゴラス数列の系譜」. Mat. Zametki . 84 (2): 281– 299. doi : 10.4213/mzm4074 .
^ ab Price, H. Lee (2008). 「ピタゴラスの樹：新種」. arXiv : 0809.4324 [math.HO].
^ ミッチェル、ダグラス W.、「92.60 に関するフィードバック」、Mathematical Gazette 93、2009 年 7 月、358–9 ページ。
^ サンダース、ロバート・A.; ランドール、トレバー（1994年7月）「ピタゴラスの三つ組の系図再考」、数学ガゼット、78 : 190–193、doi :10.2307/3618576、JSTOR 3618576、S2CID 125749577 。
^ ミッチェル、ダグラス W.、「すべての原始ピタゴラス数列の代替特性評価」、数学ガゼット85、2001年7月、273-275。

外部リンク

結び目を切る原始ピタゴラス三つ組の基礎となる三元木
フランク・R・バーンハート、H・リー・プライス、「ピタゴラスの庭、再考」、オーストラリア上級数学ジャーナル2012年1月; 26(1):29-40.[1]
ワイスタイン、エリック・W.「ピタゴラスの三つ組」。MathWorld。

[1] B. Berggren、「Pytagoreiska trianglar」（スウェーデン語）、Elementa: Tidskrift för elementär matematik、fysik och kemi 17 (1934)、129–139。根付き木については6ページをご覧ください。

[2] Barning、FJM (1963)、「Over pythagorese en bijna-pythagorese driehoeken en een Generatieprocesmet behulp van unimodulaire matrices」(オランダ語)、Math.セントラムアムステルダム空軍ズイベレウィスク。 ZW-011: 37、https://ir.cwi.nl/pub/7151

[3] A. Hall、「ピタゴラスの三つ組の系譜」、The Mathematical Gazette、第54巻、第390号、1970年12月、377～379ページ。

[4] Kanga, AR、「ピタゴラスの三つ組の家系図」『数学とその応用研究所紀要』 26、1990年1月/2月、15-17ページ。

[5] Firstov, VE (2008). 「原始対の特殊行列変換半群とピタゴラス数列の系譜」. Mat. Zametki . 84 (2): 281– 299. doi : 10.4213/mzm4074 .

[Price-6] Price, H. Lee (2008). 「ピタゴラスの樹：新種」. arXiv : 0809.4324 [math.HO].

[7] ミッチェル、ダグラス W.、「92.60 に関するフィードバック」、Mathematical Gazette 93、2009 年 7 月、358–9 ページ。

[8] サンダース、ロバート・A.; ランドール、トレバー（1994年7月）「ピタゴラスの三つ組の系図再考」、数学ガゼット、78 : 190–193、doi :10.2307/3618576、JSTOR 3618576、S2CID 125749577 。

[9] ミッチェル、ダグラス W.、「すべての原始ピタゴラス数列の代替特性評価」、数学ガゼット85、2001年7月、273-275。