プレートの振動

固定された正方形板の振動モード

板の振動は、より一般的な機械振動の問題の特殊なケースです。板の運動を支配する方程式は、板の寸法の1つが他の2つよりもはるかに小さいため、一般的な3次元物体の方程式よりも単純です。これにより、2次元板理論は、板状物体の実際の3次元運動を非常によく近似することができます。^[1]

プレートの運動を記述するために開発された理論はいくつかある。最も一般的に使用されているのは、キルヒホッフ・ラブ理論^[2]とウフライアンド・ミンドリン理論^{[3]である。 [ 4] 後者の理論については、}エリシャコフ^[5]が詳細に論じている。これらの理論によって予測される支配方程式の解は、自由条件および強制条件下におけるプレート状物体の挙動についての洞察を与える。これには、波の伝播、プレート内の定在波および振動モードの研究が含まれる。プレートの振動に関するトピックは、ライサ^{[6] 、 [7]}ゴントケビッチ^[8]ラオ^[9]ゼーデル^[10]ユ^[11]ゴーマン^{[12] [13]}ラオ^{[14]の著書で扱われている。}

キルヒホッフ・ラブプレート

キルヒホッフ・ラブ板の力学を支配する方程式は

${\displaystyle {\begin{aligned}N_{\alpha \beta ,\beta }&=J_{1}~{\ddot {u}}_{\alpha }\\M_{\alpha \beta ,\alpha \beta }+q(x,t)&=J_{1}~{\ddot {w}}-J_{3}~{\ddot {w}}_{,\alpha \alpha }\end{aligned}}}$

ここで、はプレートの中央表面の面内変位、はプレートの中央表面の横方向（面外）変位、は（上向き）の横方向荷重であり、合力とモーメントは次のように定義されます。 ${\displaystyle u_{\alpha }}$ ${\displaystyle w}$ ${\displaystyle q}$ ${\displaystyle x_{3}}$

${\displaystyle N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}\quad {\text{and}}\quad M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}\,.}$

板の厚さはであり、結果は面内応力の加重平均として定義されていることに注意されたい。支配方程式の導関数は次のように定義される。 ${\displaystyle 2h}$ ${\displaystyle \sigma _{\alpha \beta }}$

${\displaystyle {\dot {u}}_{i}:={\frac {\partial u_{i}}{\partial t}}~;~~{\ddot {u}}_{i}:={\frac {\partial ^{2}u_{i}}{\partial t^{2}}}~;~~u_{i,\alpha }:={\frac {\partial u_{i}}{\partial x_{\alpha }}}~;~~u_{i,\alpha \beta }:={\frac {\partial ^{2}u_{i}}{\partial x_{\alpha }\partial x_{\beta }}}}$

ここで、ラテン添字は1から3まで、ギリシャ添字は1から2までです。繰り返し添字の和は暗黙的に求められます。座標は面外ですが、座標と座標は面内です。厚さが均一で質量密度が均一な均一な板の場合、${\displaystyle x_{3}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle 2h}$ ${\displaystyle \rho }$

${\displaystyle J_{1}:=\int _{-h}^{h}\rho ~dx_{3}=2\rho h\quad {\text{and}}\quad J_{3}:=\int _{-h}^{h}x_{3}^{2}~\rho ~dx_{3}={\frac {2}{3}}\rho h^{3}\,.}$

等方性キルヒホッフ・ラブ板

等方性かつ均質な板の場合、応力-ひずみ関係は

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}\,.}$

ここで、は面内ひずみ、は材料の ポアソン比である。キルヒホッフ・ラブ板のひずみ-変位関係は、${\displaystyle \varepsilon _{\alpha \beta }}$ ${\displaystyle \nu }$

${\displaystyle \varepsilon _{\alpha \beta }={\frac {1}{2}}(u_{\alpha ,\beta }+u_{\beta ,\alpha })-x_{3}\,w_{,\alpha \beta }\,.}$

したがって、これらの応力に対応する合成モーメントは

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}w_{,11}\\w_{,22}\\w_{,12}\end{bmatrix}}}$

面内変位を無視すると、支配方程式は次のように簡約される。 ${\displaystyle u_{\alpha \beta }}$

${\displaystyle D\nabla ^{2}\nabla ^{2}w=q(x,t)-2\rho h{\ddot {w}}\,}$

ここで、板の曲げ剛性である。厚さが均一な板の場合、 ${\displaystyle D}$ ${\displaystyle 2h}$

${\displaystyle D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\,.}$

上記の式は別の表記法でも表すことができます。

${\displaystyle \mu \Delta \Delta w-{\hat {q}}+\rho w_{tt}=0\,.}$

固体力学では、板はしばしば2次元弾性体としてモデル化され、その位置エネルギーは、板が平面構成からどのように曲げられるかによって決まり、どのように伸ばされるかによって決まる（ドラムヘッドのような膜の場合、これは当てはまりません）。このような状況では、振動する板は振動するドラムに類似した方法でモデル化できます。しかし、結果として得られる偏微分方程式は、平衡位置からの板の垂直変位wについて、 wのラプラシアンの2乗を含む2次ではなく4次であり、その質的挙動は円形膜ドラムとは根本的に異なります。

等方性板の自由振動

自由振動の場合、外力qはゼロであり、等方性板の支配方程式は次のように簡約される。

${\displaystyle D\nabla ^{2}\nabla ^{2}w=-2\rho h{\ddot {w}}}$

または

${\displaystyle \mu \Delta \Delta w+\rho w_{tt}=0\,.}$

この関係は、板の曲率を考慮することで別の方法で導くことができる。^[15]板の 位置エネルギー密度は板の変形の仕方に依存し、板の平均曲率とガウス曲率もそれに依存する。小さな変形の場合、平均曲率はw（板の運動平衡からの垂直変位）を用いてwのラプラシアンΔwとして表され、ガウス曲率はモンジュ・アンペール演算子w _xx w _yy − wで表される。 ²
_xy板の全位置エネルギーΩは、したがって次の式で表される。

${\displaystyle U=\int _{\Omega }[(\Delta w)^{2}+(1-\mu )(w_{xx}w_{yy}-w_{xy}^{2})]\,dx\,dy}$

全体的に重要でない正規化定数は別として、μは材料の特性に依存する定数です。

運動エネルギーは次のような積分で与えられる。

${\displaystyle T={\frac {\rho }{2}}\int _{\Omega }w_{t}^{2}\,dx\,dy.}$

ハミルトンの原理は、 wが全エネルギーT + Uの変化に対して定常点であることを主張する。結果として得られる偏微分方程式は

${\displaystyle \rho w_{tt}+\mu \Delta \Delta w=0.\,}$

円形プレート

自由に振動する円板の場合、円筒座標におけるラプラシアンは次の形をとる。 ${\displaystyle w=w(r,t)}$

${\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)\,.}$

したがって、厚さのある円板の自由振動の支配方程式は ${\displaystyle 2h}$

${\displaystyle {\frac {1}{r}}{\frac {\partial }{\partial r}}\left[r{\frac {\partial }{\partial r}}\left\{{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)\right\}\right]=-{\frac {2\rho h}{D}}{\frac {\partial ^{2}w}{\partial t^{2}}}\,.}$

拡大すると、

${\displaystyle {\frac {\partial ^{4}w}{\partial r^{4}}}+{\frac {2}{r}}{\frac {\partial ^{3}w}{\partial r^{3}}}-{\frac {1}{r^{2}}}{\frac {\partial ^{2}w}{\partial r^{2}}}+{\frac {1}{r^{3}}}{\frac {\partial w}{\partial r}}=-{\frac {2\rho h}{D}}{\frac {\partial ^{2}w}{\partial t^{2}}}\,.}$

この方程式を解くには、変数分離の考え方を用い、次のような解を仮定する。

${\displaystyle w(r,t)=W(r)F(t)\,.}$

この仮定の解を支配方程式に代入すると、

${\displaystyle {\frac {1}{\beta W}}\left[{\frac {d^{4}W}{dr^{4}}}+{\frac {2}{r}}{\frac {d^{3}W}{dr^{3}}}-{\frac {1}{r^{2}}}{\frac {d^{2}W}{dr^{2}}}+{\frac {1}{r^{3}}}{\frac {dW}{dr}}\right]=-{\frac {1}{F}}{\cfrac {d^{2}F}{dt^{2}}}=\omega ^{2}}$

ここでは定数、 である。右辺の方程式の解は ${\displaystyle \omega ^{2}}$ ${\displaystyle \beta :=2\rho h/D}$

${\displaystyle F(t)={\text{Re}}[Ae^{i\omega t}+Be^{-i\omega t}]\,.}$

左辺の式は次のように書ける。

${\displaystyle {\frac {d^{4}W}{dr^{4}}}+{\frac {2}{r}}{\frac {d^{3}W}{dr^{3}}}-{\frac {1}{r^{2}}}{\frac {d^{2}W}{dr^{2}}}+{\frac {1}{r^{3}}}{\cfrac {dW}{dr}}=\lambda ^{4}W}$

ここで、この固有値問題の、板に適切な 一般解は次の式で表される。${\displaystyle \lambda ^{4}:=\beta \omega ^{2}}$

${\displaystyle W(r)=C_{1}J_{0}(\lambda r)+C_{2}I_{0}(\lambda r)}$

ここで、は0次の第一種ベッセル関数、は0次の第一種修正ベッセル関数である。定数と定数は境界条件から決定される。半径が で円周が固定された板の場合、境界条件は以下の通りである。 ${\displaystyle J_{0}}$ ${\displaystyle I_{0}}$ ${\displaystyle C_{1}}$ ${\displaystyle C_{2}}$ ${\displaystyle a}$

${\displaystyle W(r)=0\quad {\text{and}}\quad {\cfrac {dW}{dr}}=0\quad {\text{at}}\quad r=a\,.}$

これらの境界条件から、

${\displaystyle J_{0}(\lambda a)I_{1}(\lambda a)+I_{0}(\lambda a)J_{1}(\lambda a)=0\,.}$

この方程式を解くと（根は無限に存在する）、モード周波数を求めることができる。また、変位は次のように表すことができる。 ${\displaystyle \lambda _{n}}$ ${\displaystyle \omega _{n}=\lambda _{n}^{2}/{\sqrt {\beta }}}$

${\displaystyle w(r,t)=\sum _{n=1}^{\infty }C_{n}\left[J_{0}(\lambda _{n}r)-{\frac {J_{0}(\lambda _{n}a)}{I_{0}(\lambda _{n}a)}}I_{0}(\lambda _{n}r)\right][A_{n}e^{i\omega _{n}t}+B_{n}e^{-i\omega _{n}t}]\,.}$

与えられた周波数において、上式の和の最初の項はモード形状を与えます。フーリエ成分の直交性を利用することで、適切な境界条件と係数を用いて初期条件から の値を見つけることができます。 ${\displaystyle \omega _{n}}$ ${\displaystyle C_{n}}$ ${\displaystyle r=0}$ ${\displaystyle A_{n}}$ ${\displaystyle B_{n}}$

• 
  モードn = 1
• 
  モードn = 2

長方形のプレート

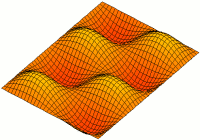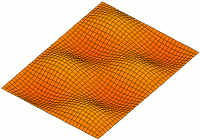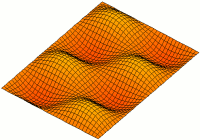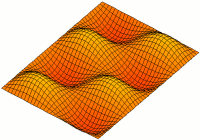
長方形板の振動モード。

-平面に寸法があり、 -方向に厚さがある長方形板を考えます。板の自由振動モードを求めます。 ${\displaystyle a\times b}$ ${\displaystyle (x_{1},x_{2})}$ ${\displaystyle 2h}$ ${\displaystyle x_{3}}$

次のような変位場を仮定する。

${\displaystyle w(x_{1},x_{2},t)=W(x_{1},x_{2})F(t)\,.}$

それから、

${\displaystyle \nabla ^{2}\nabla ^{2}w=w_{,1111}+2w_{,1212}+w_{,2222}=\left[{\frac {\partial ^{4}W}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}W}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}W}{\partial x_{2}^{4}}}\right]F(t)}$

そして

${\displaystyle {\ddot {w}}=W(x_{1},x_{2}){\frac {d^{2}F}{dt^{2}}}\,.}$

これらを支配方程式に代入すると、

${\displaystyle {\frac {D}{2\rho hW}}\left[{\frac {\partial ^{4}W}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}W}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}W}{\partial x_{2}^{4}}}\right]=-{\frac {1}{F}}{\frac {d^{2}F}{dt^{2}}}=\omega ^{2}}$

ここでは定数である。なぜなら、左辺は に独立しているが、右辺は に独立しているからである。右辺から、 ${\displaystyle \omega ^{2}}$ ${\displaystyle t}$ ${\displaystyle x_{1},x_{2}}$

${\displaystyle F(t)=Ae^{i\omega t}+Be^{-i\omega t}\,.}$

左側から、

${\displaystyle {\frac {\partial ^{4}W}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}W}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}W}{\partial x_{2}^{4}}}={\frac {2\rho h\omega ^{2}}{D}}W=:\lambda ^{4}W}$

どこ

${\displaystyle \lambda ^{2}=\omega {\sqrt {\frac {2\rho h}{D}}}\,.}$

上式は重調和固有値問題なので、次のようなフーリエ展開解を求める。

${\displaystyle W_{mn}(x_{1},x_{2})=\sin {\frac {m\pi x_{1}}{a}}\sin {\frac {n\pi x_{2}}{b}}\,.}$

この解は、単純に支持されたエッジを持つ自由に振動する長方形板の境界条件を満たしていることがわかります。

${\displaystyle {\begin{aligned}w(x_{1},x_{2},t)=0&\quad {\text{at}}\quad x_{1}=0,a\quad {\text{and}}\quad x_{2}=0,b\\M_{11}=D\left({\frac {\partial ^{2}w}{\partial x_{1}^{2}}}+\nu {\frac {\partial ^{2}w}{\partial x_{2}^{2}}}\right)=0&\quad {\text{at}}\quad x_{1}=0,a\\M_{22}=D\left({\frac {\partial ^{2}w}{\partial x_{2}^{2}}}+\nu {\frac {\partial ^{2}w}{\partial x_{1}^{2}}}\right)=0&\quad {\text{at}}\quad x_{2}=0,b\,.\end{aligned}}}$

この解を重調和方程式に代入すると、

${\displaystyle \lambda ^{2}=\pi ^{2}\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)\,.}$

前の式と比較すると、無限の数の解が存在することが分かります。 ${\displaystyle \lambda ^{2}}$

${\displaystyle \omega _{mn}=\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right){\sqrt {\frac {D\pi ^{4}}{2\rho h}}}\,.}$

したがって、プレート方程式の一般解は

${\displaystyle w(x_{1},x_{2},t)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\sin {\frac {m\pi x_{1}}{a}}\sin {\frac {n\pi x_{2}}{b}}\left(A_{mn}e^{i\omega _{mn}t}+B_{mn}e^{-i\omega _{mn}t}\right)\,.}$

との値を求めるには、初期条件とフーリエ成分の直交性を用います。例えば、 ${\displaystyle A_{mn}}$ ${\displaystyle B_{mn}}$

${\displaystyle w(x_{1},x_{2},0)=\varphi (x_{1},x_{2})\quad {\text{on}}\quad x_{1}\in [0,a]\quad {\text{and}}\quad {\frac {\partial w}{\partial t}}(x_{1},x_{2},0)=\psi (x_{1},x_{2})\quad {\text{on}}\quad x_{2}\in [0,b]}$

私たちは、

${\displaystyle {\begin{aligned}A_{mn}&={\frac {4}{ab}}\int _{0}^{a}\int _{0}^{b}\varphi (x_{1},x_{2})\sin {\frac {m\pi x_{1}}{a}}\sin {\frac {n\pi x_{2}}{b}}dx_{1}dx_{2}\\B_{mn}&={\frac {4}{ab\omega _{mn}}}\int _{0}^{a}\int _{0}^{b}\psi (x_{1},x_{2})\sin {\frac {m\pi x_{1}}{a}}\sin {\frac {n\pi x_{2}}{b}}dx_{1}dx_{2}\,.\end{aligned}}}$

参考文献

1. Reddy, JN, 2007,弾性プレートとシェルの理論と分析、CRC Press、Taylor and Francis。
2. AEH Love、「弾性殻の微小自由振動と変形について」、王立協会哲学訳（ロンドン）、1888年、第A巻、第17号、p.491–549。
3. Uflyand, Ya. S.,1948, 梁と板の横振動による波動伝播, PMM: Journal of Applied Mathematics and Mechanics, Vol. 12, pp. 287-300 (ロシア語)
4. Mindlin, RD 1951, 回転慣性とせん断が等方性弾性板の曲げ運動に及ぼす影響、ASME応用力学ジャーナル、第18巻、pp. 31–38
5. Elishakoff, I., 2020, Timoshenko-Ehrenfest Beam and Uflyand-Mindlin Plate Theories Handbook , World Scientific, Singapore, ISBN 978-981-3236-51-6
6. Leissa, AW, 1969, プレートの振動, NASA SP-160, ワシントンD.C.: 米国政府印刷局
7. Leissa、AW および Qatu、MS、2011、連続システムの振動、ニューヨーク: Mc Graw-Hill
8. Gontkevich, VS, 1964, Natural Vibrations of Plates and Shells, Kiev: “Naukova Dumka” Publishers, 1964 (ロシア語); (英訳: Lockheed Missiles & Space Co., Sunnyvale, CA)
9. ラオ、SS、連続システムの振動、ニューヨーク：ワイリー
10. Soedel, W., 1993, Vibrations of Shells and Plates, New York: Marcel Dekker Inc., (第2版)
11. Yu, YY, 1996, 弾性板の振動, ニューヨーク: Springer
12. Gorman, D., 1982, 長方形板の自由振動解析, アムステルダム: Elsevier
13. Gorman, DJ, 1999, 重ね合わせ法による板の振動解析、シンガポール：World Scientific
14. ラオ、JS、1999年、「ダイナミクス・オブ・プレート」、ニューデリー：ナロサ出版社
15. クーラント、リチャード；ヒルベルト、デイヴィッド（1953）『数理物理学の方法』第1巻、インターサイエンス出版社、ニューヨーク、NY、MR  0065391

参照

• 曲げ
• 板の曲げ
• クラドニ図形
• 微小ひずみ理論
• キルヒホッフ・ラブプレート理論
• 線形弾性
• ミンドリン・ライスナープレート理論
• プレート理論
• 応力（力学）
• 応力結果
• 構造音響