台形

台形（アメリカ英語）台形（イギリス英語）
台形または台形
タイプ四角形
エッジと頂点4
エリア12（1つの+b）h{\displaystyle {\tfrac {1}{2}}(a+b)h}
プロパティ凸状

幾何学において、台形（とらぺそどう、台形とも表記、北米英語では / ˈ t r æ p ə z ɔɪ d / ）、イギリス英語ではトラペジウム（台形とも表記、トラペジウムとも表記、英語では/ t r ə ˈ p iː z i ə m /） [ 1 ] [ 2 ]は、少なくとも1組の平行な辺を持つ四辺形である。

平行な辺は台形の底辺と呼ばれます。 [ 3 ]他の2辺は脚[ 3 ]または側面と呼ばれます。台形が平行四辺形である場合、底辺と脚の選択は任意です。

ユークリッド幾何学において、台形は通常、凸四辺形とみなされますが、交差する場合もあります。図形ABCDが凸台形であれば、ABDCは交差台形です。この記事で紹介する計量公式は、凸台形にも適用されます。

定義

台形は排他的または包括的に定義できる。排他的定義では、台形とは正確に 1組の平行辺を持ち、もう 1 組の向かい合う辺が平行ではない四辺形である。ひし形、長方形、正方形などの平行四辺形は台形とはみなされない。[ 4 ] [ 5 ]包括的定義では、台形とは少なくとも1 組の平行辺を持つ四辺形である。 [ 6 ]包括的分類法では、定義は階層的である。正方形は長方形とひし形の一種であり、長方形またはひし形は平行四辺形の一種であり、すべての平行四辺形は台形の一種である。[ 7 ]台形は平行四辺形以外の四辺形として定義することもできる。この定義も排他的であり、ユークリッドの『原論』で使用されている。

専門の数学者や中等教育の幾何学の教科書では、幾何学の定理の記述や証明が簡略化されるため、ほとんどの場合、包括的な定義と分類が好まれます。[ 8 ]初等中等教育では、長方形と平行四辺形の定義もほとんどの場合包括的ですが、台形については排他的な定義がよく見られます。[ 9 ] [ 10 ]この記事では、包括的な定義を使用し、平行四辺形を台形の特別な種類と見なします。（四辺形§分類を参照 ）

混乱を避けるため、いくつかの文献では、正確に1組の平行辺を持つ台形を表すために「適切な台形」という用語を使用しています。これは、他の数学的対象における「適切な」という単語の用法に似ています。 [ 11 ] [ 12 ]

語源

古代ギリシャ幾何学のユークリッドの『原論』（紀元前300年頃）では、四辺形は 正方形、長方形（正方形ではない長方形）、（正方形ではない）菱形、菱形（菱形ではない長方形ではない平行四辺形）、台形（τραπέζιον、文字通り「台形」）の3つのカテゴリーに分類されていました。台形は、前述のカテゴリーに含まれない四辺形です。[ 13 ]

新プラトン主義の哲学者プロクロス（紀元5世紀半ば）は、より豊富な範疇を備えたユークリッドの注釈書を著し、その著作をポセイドニオス（紀元前 100年頃）に帰した。この体系では、四辺形は平行四辺形または非平行四辺形のいずれかである。平行四辺形自体は、正方形、長方形（正方形ではない長方形）、菱形、または菱形（菱形でも長方形でもない）のいずれかである。非平行四辺形は、ちょうど1組の平行辺を持つ台形（二等辺三角形（等しい辺を持つ）または不等辺三角形（不等辺三角形）のいずれか）である。あるいは、平行辺を持たない台形（τραπεζοειδή、文字通り「テーブルのような」）である。[ 13 ] [ 14 ]

1795年のハットンの定義

アメリカ英語を除くすべてのヨーロッパ言語は、プロクロスの台形と台形の意味に従っています。[ 15 ]しかし、イギリス英語では19世紀のほとんどの期間、意味が逆でした。1795年、チャールズ・ハットンが出版した影響力のある数学辞典で、2つの用語が説明なしに入れ替わったため、広範囲にわたる矛盾が生じました。ハットンの変更はイギリス英語では1875年頃に元に戻されましたが、アメリカ英語では現在まで維持されています。[ 13 ] 19世紀後半のアメリカの幾何学の教科書では、台形は平行な辺を持たないもの、台形はちょうど1組の平行辺を持つもの、平行四辺形は2組の向かい合う平行辺を持つものと定義しています。[ 3 ] [ 16 ]イギリスとアメリカで台形と台形 の意味が矛盾しているため混乱を避けるため、平行な辺を持たない四辺形は不規則な四辺形と呼ばれることがあります。[ 17 ]

特殊なケース

台形の特殊なケース。オレンジ色の図形は平行四辺形としても分類されます。

等脚台形は、底角が同じ大きさの台形です。[ 18 ] [ 19 ]結果として、2 つの脚の長さも等しく、鏡映対称性があります。[ 20 ]これは、長方形としての鋭角台形または直角台形で可能です。鋭角台形とは、長い方の底辺に 2 つの隣接する鋭角がある台形で、等脚台形は鋭角台形の一例です。等脚台形には、3 辺台形と呼ばれる特殊なケースがあり、これは、2 つの台形の脚の長さが台形の上部の底辺と等しい台形であることを意味します。[ 21 ]等脚台形は、交差した四辺形の一種である逆平行四辺形の凸包です。あらゆる反平行四辺形は、2つの平行な辺を2つの対角線に置き換えることによって、このような台形から形成されます。[ 22 ]

一方、鈍角台形は、各底辺に鋭角と鈍角がそれぞれ1つずつあります。例としては、鋭角が等しい平行四辺形が挙げられます。 [ 21 ]

直角台形は、隣接する2つの直角を持つ台形です。直角台形の特殊な例として、3つの直角三角形で形成されるものがあります[ 23 ]。これはジェームズ・ガーフィールドがピタゴラスの定理を証明するために用いました[ 24 ]。

接線台形は内接円を持つ台形です。

存在の条件

4つの長さa、c、b、dは、 aとbが平行である非平行四辺形台形の連続する辺を構成できるのは、[ 25 ]の場合のみである。

|d−c|<|b−1つの|<d+c。{\displaystyle \displaystyle |dc|<|ba|<d+c.}

のときは四辺形は平行四辺形であるが、のときは（台形ではない）外接四辺形である。[ 26 ]d−c＝b−1つの＝0{\displaystyle dc=ba=0}|d−c|＝|b−1つの|≠0{\displaystyle |dc|=|ba|\neq 0}

特徴づけ

一般的な台形:平行な辺: 脚付き : 対角線: 中央線: 高さ: 1つの、b{\displaystyle a,\,b}1つの<b{\displaystyle a<b}c、d{\displaystyle c,\,d}q、p{\displaystyle q,\,p}メートル{\displaystyle m}h{\displaystyle h}
対角線によって形成される対向三角形を持つ台形S、T{\displaystyle S,\,T}

凸四辺形が与えられた場合、次の特性は同等であり、それぞれ四辺形が台形であることを意味します。

  • 2 つの隣接する角度は補角であり、合計すると 180度になります。
  • 辺と対角線の間の角度は、反対側の辺と同じ対角線の間の角度に等しくなります。
  • 対角線は互いに同じ比率で切断されます（この比率は平行な辺の長さ間の比率と同じです）。
  • 対角線は四辺形を4つの三角形に分割し、そのうちの1組の向かい合う三角形は面積が等しい。[ 27 ]
  • 一方の対角線によって形成される２つの三角形の面積の積は、もう一方の対角線によって形成される２つの三角形の面積の積に等しい。[ 28 ]
  • 対角線によって形成される4つの三角形のうち、向かい合う2つの三角形の面積SとTは次の式を満たす。
K＝S+T、{\displaystyle {\sqrt {K}}={\sqrt {S}}+{\sqrt {T}},}
ここでKは四辺形の面積である。[ 29 ]
  • 台形の２つの対角線の中点と対角線の交点は同一直線上にある。[ 30 ]
  • 四辺形ABCDの角は[ 31 ]を満たす。罪⁡あ罪⁡C＝罪⁡B罪⁡D。{\displaystyle \sin A\sin C=\sin B\sin D.}
  • 隣接する2つの角度の余弦の合計は0になり、他の2つの角度の余弦も0になります。[ 31 ]
  • 隣接する2つの角度のコタンジェントの合計は0になり、他の隣接する2つの角度のコタンジェントの合計も0になります。[ 32 ]
  • 一つの二中線は四辺形を面積の等しい二つの四辺形に分割する。[ 32 ]
  • 向かい合う２辺の中点を結ぶ二中線の長さの２倍は、他の辺の長さの合計に等しい。[ 33 ]

さらに、次の特性は同等であり、それぞれ対辺aとbが平行であることを意味します。

  • 連続する辺a、c、b、dと対角線p、qは次式を満たす[ 34 ]
p2+q2＝c2+d2+21つのb。{\displaystyle p^{2}+q^{2}=c^{2}+d^{2}+2ab.}
  • 対角線の中点間の距離vは次の式を満たす[ 35 ]
v＝|1つの−b|2。{\displaystyle v={\frac {|ab|}{2}}.}

プロパティ

胴体中央部と高さ

台形の中線は、台形の脚の中点を結ぶ線分である。台形の底辺と平行であり、その長さmは台形の底辺aと底辺bの長さの平均に等しい。 [ 36 ] [ 19 ] [ 37 ] [ 6 ]

メートル＝1つの+b2。{\displaystyle m={\frac {a+b}{2}}.}

台形の中線は、2 つの双中線のうちの 1 つです(もう 1 つの双中線は台形を等しい面積に分割します)。

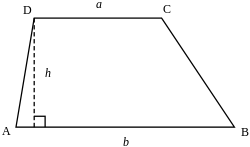
高さ（または高度）は、底辺間の垂直距離です。 [ 3 ] 2つの底辺の長さが異なる場合（a ≠ b）、台形の高さhは、その4辺の長さから次の式で決定できます[ 38 ]

h＝（p−21つの）（p−2b）（p−2b−2d）（p−2b−2c）2|b−1つの|{\displaystyle h={\frac {\sqrt {(p-2a)(p-2b)(p-2b-2d)(p-2b-2c)}}{2|ba|}}}

ここで、cとd はそれぞれ脚の長さ、 です。 p＝1つの+b+c+d{\displaystyle p=a+b+c+d}

エリア

台形の面積は、中線（2つの底辺の平均）と高さの積で与えられます。 ここで、とは底辺の長さ、 は高さ（これらの辺の間の垂直距離）です。[ 39 ]この方法は、インドの古典時代にアーリヤバタの『アーリヤバティーヤ』（第2.8節）で使用され、三角形を、平行な辺の1つが点に縮んだ退化した台形と見なすことで、特別なケースとして三角形の面積のよく知られた公式が得られました。 K{\displaystyle K}K＝12（1つの+b）h{\displaystyle K={\tfrac {1}{2}}(a+b)h}1つの{\displaystyle a}b{\displaystyle b}h{\displaystyle h}

7世紀のインドの数学者バースカラ1世は、連続する辺が、、、::である台形の面積について次の公式を導き出しました。 ここで、とが平行で、です。[ 40 ]この公式は、 より対称的なバージョンに因数分解することができます[ 38 ]1つの{\displaystyle a}c{\displaystyle c}b{\displaystyle b}d{\displaystyle d}K＝12（1つの+b）c2−14（（b−1つの）+c2−d2b−1つの）2{\displaystyle K={\frac {1}{2}}(a+b){\sqrt {c^{2}-{\frac {1}{4}}\left((ba)+{\frac {c^{2}-d^{2}}{ba}}\right)^{2}}}}1つの{\displaystyle a}b{\displaystyle b}b>1つの{\displaystyle b>a}

K＝1つの+b4|b−1つの|（−1つの+b+c+d）（1つの−b+c+d）（1つの−b+c−d）（1つの−b−c+d）。{\displaystyle K={\frac {a+b}{4|ba|}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+cd)(ab-c+d)}}.}

平行な辺の 1 つが点 ( a = 0とします) に縮小すると、この式は三角形の面積に関する ヘロンの式になります。

ヘロンの式によく似た、面積に関する別の式は[ 38 ]である。

K＝1つの+b|b−1つの|（s−b）（s−1つの）（s−b−c）（s−b−d）{\displaystyle K={\frac {a+b}{|ba|}}{\sqrt {(sb)(sa)(sbc)(sbd)}}}

ここで、 は台形の半周長です。(この公式はBrahmaguptaの公式に似ていますが、台形は円周ではない(円に内接しない)可能性がある点で異なります。この公式は、一般的な四辺形に対するBretschneiderの公式の特殊なケースでもあります。) s＝12（1つの+b+c+d）{\displaystyle s={\tfrac {1}{2}}(a+b+c+d)}

ブレトシュナイダーの公式から、

K＝（1つのb2−1つの2b−1つのd2+bc2）（1つのb2−1つの2b−1つのc2+bd2）4（b−1つの）2−（c2+d2−1つの2−b24）2。{\displaystyle K={\sqrt {{\frac {\left(ab^{2}-a^{2}b-ad^{2}+bc^{2}\right)\left(ab^{2}-a^{2}b-ac^{2}+bd^{2}\right)}{4(ba)^{2}}}-\left({\frac {c^{2}+d^{2}-a^{2}-b^{2}}{4}}\right)^{2}}}.}

平行な辺を結ぶ二中線は面積を二等分します。より一般的には、中線の中点を通り、底辺と平行で、底辺と交わる線は面積を二等分します。また、一方の辺の両端ともう一方の辺の中点を結ぶ三角形も面積の半分となります。[ 41 ]

対角線

対角線の長さは、 が短底、が長底、が台形の脚である。[ 42 ]p＝1つのb2−1つの2b−1つのc2+bd2b−1つの、q＝1つのb2−1つの2b−1つのd2+bc2b−1つの、{\displaystyle {\begin{aligned}p&={\sqrt {\frac {ab^{2}-a^{2}b-ac^{2}+bd^{2}}{ba}}},\\q&={\sqrt {\frac {ab^{2}-a^{2}b-ad^{2}+bc^{2}}{ba}}},\end{aligned}}}1つの{\displaystyle a}b{\displaystyle b}c{\displaystyle c}d{\displaystyle d}

台形を対角線ACとBD（右図参照）で4つの三角形に分割し、Oで交差させると、 AODの面積はBOCの面積に等しく、 AODとBOCの面積の積はAOBとCODの面積の積に等しくなります。隣接する三角形の面積の比は、平行な辺の長さの比と同じです。[ 38 ]△{\displaystyle \triangle }△{\displaystyle \triangle }△{\displaystyle \triangle }△{\displaystyle \triangle }△{\displaystyle \triangle }△{\displaystyle \triangle }

⁠ ⁠ をℓ{\displaystyle \ell}、対角線の交点を通り、各辺に1つの端点を持つ底辺に平行な線分の長さとすると、 ⁠ ⁠ℓ{\displaystyle \ell}は底辺の長さの調和平均である。 [ 43 ]

1ℓ＝12（11つの+1b）。{\displaystyle {\frac {1}{\ell}}={\frac {1}{2}}\left({\frac {1}{a}}+{\frac {1}{b}}\right).}

平行でない延長された辺の交点と対角線の交点を通る線は、各底辺を二等分する。[ 44 ]

その他の特性

面積の中心（均一な薄板の質量の中心）は、平行な辺の中点を結ぶ線分上にあり、長辺bから垂直な距離xのところに位置し、 [ 45 ]で与えられる。

×＝h3（21つの+b1つの+b）。{\displaystyle x={\frac {h}{3}}\left({\frac {2a+b}{a+b}}\right).}

面積の中心は、この部分を（短辺から長辺にかけて）の比率で分割します[ 46 ]：p.862

1つの+2b21つの+b。{\displaystyle {\frac {a+2b}{2a+b}}.}

角Aと角Bの二等分線がPで交差し、角Cと角Dの二等分線がQで交差する場合、[ 44 ]

P質問＝|あD+BC−あB−CD|2。{\displaystyle PQ={\frac {|AD+BC-AB-CD|}{2}}.}

アプリケーション

数値積分における台形則
ニューヨーク市のメトロポリタン美術館にあるデンドゥール神殿
トウダイグサに描かれた台形の前胸背板の例
オンタリオ州道502号線

微積分学では、関数の定積分は、積分区間を小さな均一区間に 分割し、各区間における関数の値をその端点における値の平均として近似することにより、離散和として数値的に近似することができる。 ここで、 は区間の数、、、 である。図的に言えば、これは関数のグラフの下の領域を台形の集合で近似することに相当するため、この方法は台形定理と呼ばれる。[ 47 ]f（×）{\displaystyle f(x)}∫1つのbf（×）d×≈∑け＝1北12（f（×け−1）+f（×け））Δ×、{\displaystyle \int _{a}^{b}f(x)\,dx\approx \sum _{k=1}^{N}{\tfrac {1}{2}}{\bigl (}f(x_{k-1})+f(x_{k}){\bigr )}\Delta x,}北{\displaystyle N}×0＝1つの{\displaystyle x_{0}=a}×北＝b{\displaystyle x_{N}=b}Δ×＝（b−1つの）/北{\displaystyle \Delta x=(b-a)/N}

長方形を、一方の軸を中心に置き、もう一方の軸を中心としない位置から遠近法で見ると、等脚台形に見えます。アーチ型のキーストーンが一般的に台形であることから、この効果はキーストーン効果と呼ばれます。例えば、長方形の建物の正面を、直線レンズを用いて地上から正面から撮影すると、建物の像は等脚台形になります。このような写真には、長方形の形状を復元するために「キーストーン変換」が適用される場合があります。ビデオプロジェクターでは、投影前に記録された画像にこのようなキーストーン変換を適用することがあり、平面スクリーンに投影された画像は歪みがありません。

真上から見たカンピドリオ広場。

台形のドアや窓はインカでは標準的なスタイルだったが、同地域の以前の文化でも使われていたことがわかっており、必ずしもインカに起源を持つわけではない。[ 48 ] [ 49 ]ムーア建築の特徴である胸壁である アルメナは台形である。[ 50 ] ミケランジェロがカンピドリオ広場を再設計した際（右の写真参照）、台形が楕円を囲むように取り入れられ、地上レベルで短縮して見ると正方形が円を囲んでいるような効果を生み出した。[ 51 ]映画撮影法では台形を逆に利用して、カメラの視点から過剰な短縮効果を生み出し、映画スタジオの部屋に、セットの物理的な奥行きよりも大きな奥行きがあるという錯覚を与えている。[ 52 ]台形はカリガリズム の視覚的歪みを生み出すのにも使われた。[ 52 ]運河や排水溝は一般的に台形の断面を持っています。

生物学、特に形態学や分類学では、台形や台形型などの用語は特定の器官や形態を説明する際によく使われます。[ 53 ]

台形は図形記号として用いられることがあります。回路図では、台形はマルチプレクサの記号として用いられます。[ 54 ]等脚台形は道路標識の形状にも用いられ、例えばカナダのオンタリオ州の幹線道路ではその形状が用いられています。[ 55 ]

非ユークリッド幾何学

球面幾何学や双曲幾何学では、四辺形の内角の合計は 360° にはなりませんが、台形、平行四辺形、長方形に類似した四辺形を定義することはでき、さらにユークリッド幾何学では区別されない新しいタイプの四辺形もいくつかあります。

球面台形または双曲台形は、2 つの対辺 (脚) を持ち、各脚の隣接する 2 つの角度の合計が同じ量になる四辺形です。他の 2 辺は底辺です。[ 56 ]ユークリッド幾何学と同様に、特殊な例として、脚が等しい (各底辺に隣接する角度も等しい) 二等辺台形、2 組の向かい合った等しい角度と 2 組の向かい合った等しい辺を持つ平行四辺形、2 組の向かい合った等しい角度と 4 組の等しい辺を持つひし形、4 つの等しい (直角ではない) 角度と 2 組の向かい合った等しい辺を持つ長方形、4 つの等しい (直角ではない) 角度と 4 組の等しい辺を持つ正方形があります。

長方形を2辺の中点を通る線で半分に切ると、得られる2つのピースはそれぞれ2つの直角を持つ二等辺台形となり、サッケリ四辺形と呼ばれます。長方形を2つの対辺の中点を通る線で4等分すると、得られる4つのピースはそれぞれ3つの直角を持つ四辺形となり、ランベルト四辺形と呼ばれます。ユークリッド幾何学では、サッケリ四辺形とランベルト四辺形は単なる長方形です。

台形数の例: 15 = 4 + 5 + 6

台形数とは、 2つ以上の1より大きい正の整数を連続して足し合わせて台形パターンを形成する正の整数の集合である。 [ 57 ]

交差ラダー問題とは、直角台形の対角線の長さと垂直辺から対角線の交点までの距離が与えられたときに、直角台形の平行な辺間の距離を求める問題である。[ 58 ]

参照

注記

  1. ^ 「台形 – 数学用語の定義 – Math Open Reference」 www.mathopenref.com . 2024年5月15日閲覧。
  2. ^ガーディナー、アンソニー・D.、ブラッドリー、クリストファー・J. (2005). 『平面ユークリッド幾何学：理論と問題点』 英国数学財団. p. 34. ISBN 9780953682362。
  3. ^ a b c dホプキンス 1891、33ページ。
  4. ^ Usiskin & Griffin 2008、29ページ 。
  5. ^アルシーナ & ネルセン 2020、p.  90．
  6. ^ a bリンゲンバーグ、ローレンス・A. (1977). 「平面上の座標」.大学幾何学. REクリーガー出版社. pp.  161– 162. ISBN 9780882755458。
  7. ^アルシーナ & ネルセン 2020、p.  89 .
  8. ^ Usiskin & Griffin 2008、32ページ 。
  9. ^ Craine, Timothy V.; Rubenstein, Rheta N. (1993). 「幾何学学習を促進する四辺形階層」.数学教師. 86 (1): 30– 36. doi : 10.5951/MT.86.1.0030 . JSTOR 27968085 . 
  10. ^ポポヴィッチ、ゴルヤナ (2012). 「この台形とは一体誰なのか？」.中学校における数学教育. 18 (4): 196– 199. doi : 10.5951/mathteacmiddscho.18.4.0196 . JSTOR 10.5951/mathteacmiddscho.18.4.0196 . ResearchGate : 259750174 . 
  11. ^ミション、ジェラール・P. 「歴史と命名法」 。 2023年6月9日閲覧。
  12. ^ビーム、ジョン・K. (2006). 『幾何学のつながり：中学校教師のための数学』 . 教師のための数学コースにおけるつながり. ピアソン・プレンティス・ホール. p. 57. ISBN 9780131449268。
  13. ^ a b cマレー、ジェームズ (1926). 「トラペジウム」 . 『歴史原理に基づく新英語辞典：主に哲学協会収集資料に基づく』 . 第10巻. オックスフォード大学クラレンドン出版. p. 286. また「トラペゾイド」pp. 286–287も参照.
  14. ^モロー、グレン・R.編 (1970).プロクロス：ユークリッド原論第一巻注釈. プリンストン大学出版局. §§169–174, pp. 133–137 .
  15. ^コンウェイ、バーギエル、グッドマン・ストラウス2016、286ページ 。
  16. ^ホッブズ 1899、66ページ。
  17. ^デイヴィス、チャールズ(1873). 『数学の性質と効用』ニューヨーク: AS Barnes & Company. p. 35.
  18. ^ダッジ 2012、82ページ。
  19. ^ a bポサマンティエ, アルフレッド・S.; バニスター, ロバート・L. (2014). 「台形」.幾何学、その要素と構造：第2版. ドーバー数学ブックス（第2版）. クーリエ社. §7.7, pp. 282–287. ISBN 9780486782164。
  20. ^ホプキンス 1891、34ページ。
  21. ^ a bアルシーナ & ネルセン 2020、p.  90–91。
  22. ^アルシーナ & ネルセン 2020、p.  212 .
  23. ^アルシーナ & ネルセン 2020、p.  91．
  24. ^ジェームズ、ガーフィールド(1876)。 「ポンス・アシノルム」。ニューイングランド教育ジャーナル。3 (14): 161. ISSN 2578-4145。JSTOR 44764657。  
  25. ^ Ask Dr. Math (2008)、「辺の長さのみで台形の面積を求める」。
  26. ^ヨセフソン 2013、35ページ。
  27. ^ヨセフソン 2013、提案5。
  28. ^ Josefsson 2013、Thm. 6.
  29. ^ Josefsson 2013、Thm. 8.
  30. ^ヨセフソン 2013、Thm. 15。
  31. ^ a bヨセフソン 2013、p. 25。
  32. ^ a bヨセフソン 2013、p. 26。
  33. ^ヨセフソン 2013、31ページ。
  34. ^ヨセフソン 2013、コリント11。
  35. ^ Josefsson 2013、Thm. 12。
  36. ^ホッブズ 1899、58ページ。
  37. ^ダッジ2012、117ページ 。
  38. ^ a b c d Weisstein, Eric W.「台形」。MathWorld 。
  39. ^ダッジ2012、84ページ 。
  40. ^ Puttaswamy, TK (2012). 『近代以前のインド数学者の数学的業績』 エルゼビア. p. 156. ISBN 978-0-12-397913-1。
  41. ^ホプキンス 1891、95ページ。
  42. ^アルシーナ & ネルセン 2020、p.  96．
  43. ^スキデル、アキバ (1977). 「調和平均：ノモグラフといくつかの問題点」.数学教師. 70 (1): 30– 34. doi : 10.5951/MT.70.1.0030 . JSTOR 27960699 . 
    ホーエン、ラリー (1984). 「加重平均の幾何学的解釈」 . 2年制大学数学ジャーナル. 15 (2): 135– 139. doi : 10.1080/00494925.1984.11972762 (2025年7月1日停止).{{cite journal}}: CS1 maint: DOI inactive as of July 2025 (link)
  44. ^ a b Owen Byer、Felix Lazebnik、Deirdre Smeltzer、「ユークリッド幾何学の方法」、アメリカ数学会、2010年、55ページ。
  45. ^ 「一般的な台形の重心、面積、慣性モーメント、極モーメント、回転半径」www.efunda.com . 2024年5月15日閲覧。
  46. ^アポストル、トム M.ムナツァカニアン、マミコン A. (2004 年 12 月)。「外接円の図形」（PDF）。アメリカ数学月刊誌。111 (10): 853–863 .土井: 10.2307/4145094。JSTOR 4145094 。2016 年 4 月 6 日に取得。 
  47. ^ヴァールバーグ、デール E.;パーセル、エドウィン J.リグドン、スティーブン E. (2007)。微積分学(第 9 版)。ピアソン・プレンティス・ホール。 p. 264.ISBN​ 978-0131469686。
  48. ^ 「マチュピチュ 失われたインカの都市 – インカの幾何学」gogeometry.com . 2018年2月13日閲覧。
  49. ^ Hyslop, John (2014).インカの定住計画. テキサス大学出版局. p. 54. ISBN 9780292762640。
  50. ^ Curl 1999、p.19、アルメナ。
  51. ^カール 1999 年、p. 486、ミケランジェロ・ブオナローティ。
  52. ^ a bラミレス 2012、84頁。
  53. ^ John L. Capinera (2008年8月11日). Encyclopedia of Entomology . Springer Science & Business Media. pp. 386, 1062, 1247. ISBN 978-1-4020-6242-1。
  54. ^ダニエルズ、ジェリー (1996). 『デジタルデザイン ゼロから1へ』 ジョン・ワイリー・アンド・サンズ. p. 203. ISBN 978-0-471-12447-4。
  55. ^アルシーナ & ネルセン 2020、p.  93．
  56. ^ペトロフ、FV（2009年）。Вписанные четырёхугольники и трапеции в абсолютной геометрии[絶対幾何における周期的な四角形と台形] (PDF)。マテマチェスコエ・プロスヴェシェニエ。トレティア・セリヤ（ロシア語）。13 : 149–154 .
  57. ^ゲーマー, カールトン; ローダー, デイビッド W.; ワトキンス, ジョン J. (1985). 「台形数」.数学マガジン. 58 (2): 108–110 . doi : 10.2307/2689901 . JSTOR 2689901 . 
  58. ^アルシーナ & ネルセン (2020)、p.  102 .

参考文献

  • アルシーナ、クラウディ、ネルセン、ロジャー（2020年） 『四辺形の宝庫』アメリカ数学協会。ISBN 978-1-4704-5312-1。
  • コンウェイ、ジョン・H.、バーギエル、ハイディ、グッドマン＝ストラウス、チャイム (2016). 『物の対称性』CRC Press. ISBN 978-1-4398-6489-0。
  • カール、ジェームズ・スティーブンス（1999年）『建築辞典』オックスフォード大学出版局、ISBN 9780198606789。
  • ドッジ、クレイトン・W. (2012). 『ユークリッド幾何学と変換』 ドーバー数学ブックス. クーリエ社. ISBN 9780486138428。
  • ホッブス、チャールズ・オースティン (1899). 『平面幾何学の原初』 . A. ラヴェル・アンド・カンパニー.
  • ホプキンス、ジョージ・アーヴィング (1891). 『平面幾何学マニュアル』 . DC Heath & Company.
  • Josefsson, Martin (2013). 「台形の特徴付け」(PDF) . Forum Geometricorum . 13 : 23–35 . 2013年6月16日時点のオリジナル(PDF)からのアーカイブ。
  • ウスィスキン、ザルマン、グリフィン、ジェニファー (2008). 『四辺形の分類：定義の研究』インフォメーション・エイジ・パブリッシング. pp.  49– 52, 63– 67.
  • ラミレス、フアン・アントニオ（2012年）「建築と欲望：映画構成の特徴」『スクリーンのための建築：ハリウッド黄金時代のセットデザインの批評的研究』ジョン・F・マクファーランド・モフィット訳。ISBN 9780786469307。

さらに読む

無料辞書のウィクショナリーで台形を調べてください。
「 https://en.wikipedia.org/w/index.php?title=台形&oldid =1331659771」より取得