クランク・ニコルソン法

数値解析において、クランク・ニコルソン法は、熱方程式や類似の偏微分方程式を数値的に解くために使用される有限差分法である。^{[ 1 ]}これは時間に関して2次の方法である。時間に関して暗黙的であり、暗黙的ルンゲ・クッタ法として記述でき、数値的に安定である。この方法は、1940年代にジョン・クランクとフィリス・ニコルソンによって開発された。 ^{[ 2 ]}

拡散方程式（および他の多くの方程式）では、クランク・ニコルソン法は無条件に安定であることが示されています。^{[ 3 ]}しかし、時間ステップと熱拡散率の積と空間ステップの2乗の比が大きい場合（通常、フォン・ノイマン安定性解析によれば1/2より大きい）、近似解には（減衰する）擬似振動が含まれる可能性があります。このため、大きな時間ステップや高い空間分解能が必要な場合は、精度は劣るものの、安定しており振動の影響を受けない後退オイラー法がよく使用されます。 ${\displaystyle \Delta t}$ ${\displaystyle \Delta x^{2}}$

原理

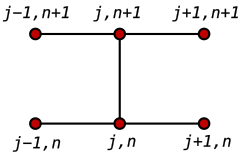
1次元問題のためのCrank-Nicolsonステンシル

クランク・ニコルソン法は台形則に基づいており、時間に関して2次の収束を示す。線形方程式の場合、台形則は暗黙的中点法（ガウス・ルジャンドル暗黙的ルンゲ・クッタ法の最も単純な例）と等価であり、幾何学的積分器としての性質も持つ。例えば、1次元において、偏微分方程式が $${\displaystyle {\frac {\partial u}{\partial t}}=F\left(u,x,t,{\frac {\partial u}{\partial x}},{\frac {\partial ^{2}u}{\partial x^{2}}}\right).}$$

およびをおよびについて評価すると、クランク・ニコルソン法の方程式は、における前進オイラー法とにおける後退オイラー法を組み合わせたものになります（ただし、後退オイラー法の方程式は解に暗黙的に依存するため、この方法自体はこれら 2 つの方法の単なる平均 ではないことに注意してください）。${\displaystyle u(i\Delta x,n\Delta t)=u_{i}^{n}}$ ${\displaystyle F_{i}^{n}=F}$ ${\displaystyle i,n}$ ${\displaystyle u_{i}^{n}}$ ${\displaystyle n}$ ${\displaystyle n+1}$

${\displaystyle {\frac {u_{i}^{n+1}-u_{i}^{n}}{\Delta t}}=F_{i}^{n}\left(u,x,t,{\frac {\partial u}{\partial x}},{\frac {\partial ^{2}u}{\partial x^{2}}}\right)}$	フォワードオイラー
${\displaystyle {\frac {u_{i}^{n+1}-u_{i}^{n}}{\Delta t}}=F_{i}^{n+1}\left(u,x,t,{\frac {\partial u}{\partial x}},{\frac {\partial ^{2}u}{\partial x^{2}}}\right)}$	逆オイラー
${\displaystyle {\frac {u_{i}^{n+1}-u_{i}^{n}}{\Delta t}}={\frac {1}{2}}\left[F_{i}^{n+1}\left(u,x,t,{\frac {\partial u}{\partial x}},{\frac {\partial ^{2}u}{\partial x^{2}}}\right)+F_{i}^{n}\left(u,x,t,{\frac {\partial u}{\partial x}},{\frac {\partial ^{2}u}{\partial x^{2}}}\right)\right]}$	クランク・ニコルソン

これは暗黙法であることに注意してください。つまり、時間的にの「次の」値を得るには、代数方程式系を解く必要があります。偏微分方程式が非線形の場合、離散化も非線形となり、時間を進めると非線形代数方程式系を解くことになりますが、線形化も可能です。多くの問題、特に線形拡散問題では、代数問題は三角行列であり、三角行列アルゴリズムを用いて効率的に解くことができます。このアルゴリズムは、通常の完全行列の場合とは対照的に、高速で直接解を与えます。ここで は行列のサイズを示します。 ${\displaystyle u}$ ${\displaystyle {\mathcal {O}}(N)}$ ${\displaystyle {\mathcal {O}}(N^{3})}$ ${\displaystyle N}$

例: 1D拡散

クランク・ニコルソン法は拡散問題によく適用されます。例えば、線形拡散の場合、

${\displaystyle {\frac {\partial u}{\partial t}}=a{\frac {\partial ^{2}u}{\partial x^{2}}},}$

右辺に 有限差分空間離散化を適用すると、クランク・ニコルソン離散化は次のようになる。

${\displaystyle {\frac {u_{i}^{n+1}-u_{i}^{n}}{\Delta t}}={\frac {a}{2(\Delta x)^{2}}}\left((u_{i+1}^{n+1}-2u_{i}^{n+1}+u_{i-1}^{n+1})+(u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n})\right)}$

または、 ${\displaystyle r={\frac {a\Delta t}{2(\Delta x)^{2}}}}$

${\displaystyle -ru_{i+1}^{n+1}+(1+2r)u_{i}^{n+1}-ru_{i-1}^{n+1}=ru_{i+1}^{n}+(1-2r)u_{i}^{n}+ru_{i-1}^{n}.}$

方程式の右側の項が既知であることを考えると、これは三重対角問題であり、よりコストのかかる逆行列演算よりも三重対角行列アルゴリズムを使用することで効率的に解くことができます。 ${\displaystyle u_{i}^{n+1}}$

次のような準線形方程式（これは最小限の例であり、一般的なものではありません）

${\displaystyle {\frac {\partial u}{\partial t}}=a(u){\frac {\partial ^{2}u}{\partial x^{2}}},}$

は非線形代数方程式系となり、上記のように簡単に解くことはできません。しかし、 の古い値、つまりの代わりに を用いることで、問題を線形化できる場合があります。また、明示的な方法を用いて を推定し、安定性を維持できる場合もあります。${\displaystyle a}$ ${\displaystyle a_{i}^{n}(u)}$ ${\displaystyle a_{i}^{n+1}(u)}$ ${\displaystyle a_{i}^{n+1}(u)}$

例: 定常流れにおける移流を伴う1D拡散、複数チャネル接続

これは、定常流下の河川や小川で汚染問題が発生しているものの、情報が1次元でしか得られない場合に、多くの目的で使用されるソリューションです。多くの場合、この問題は1次元の問題に簡略化され、それでも有用な情報が得られます。

ここでは、水中の溶質汚染物質の濃度をモデル化します。この問題は3つの部分から構成されます。既知の拡散方程式（定数 ）、移流成分（速度場によってシステムが空間的に進化することを意味します）（定数 ）、そして縦方向チャネル間の横方向相互作用（）です。 ${\displaystyle D_{x}}$ ${\displaystyle U_{x}}$ ${\displaystyle k}$

${\displaystyle {\frac {\partial C}{\partial t}}=D_{x}{\frac {\partial ^{2}C}{\partial x^{2}}}-U_{x}{\frac {\partial C}{\partial x}}-k(C-C_{N})-k(C-C_{M}),}$

1

ここで、 は汚染物質の濃度であり、下付き文字のと は前のチャネルと次のチャネルに対応します。 ${\displaystyle C}$ ${\displaystyle N}$ ${\displaystyle M}$

クランク・ニコルソン法（位置、時間を表す）は、PDE の各要素を次のように変換します。 ${\displaystyle i}$ ${\displaystyle j}$

${\displaystyle {\frac {\partial C}{\partial t}}\Rightarrow {\frac {C_{i}^{j+1}-C_{i}^{j}}{\Delta t}},}$

2

${\displaystyle {\frac {\partial ^{2}C}{\partial x^{2}}}\Rightarrow {\frac {1}{2(\Delta x)^{2}}}\left((C_{i+1}^{j+1}-2C_{i}^{j+1}+C_{i-1}^{j+1})+(C_{i+1}^{j}-2C_{i}^{j}+C_{i-1}^{j})\right),}$

3

${\displaystyle {\frac {\partial C}{\partial x}}\Rightarrow {\frac {1}{2}}\left({\frac {(C_{i+1}^{j+1}-C_{i-1}^{j+1})}{2(\Delta x)}}+{\frac {(C_{i+1}^{j}-C_{i-1}^{j})}{2(\Delta x)}}\right),}$

4

${\displaystyle C\Rightarrow {\frac {1}{2}}(C_{i}^{j+1}+C_{i}^{j}),}$

5

${\displaystyle C_{N}\Rightarrow {\frac {1}{2}}(C_{Ni}^{j+1}+C_{Ni}^{j}),}$

6

${\displaystyle C_{M}\Rightarrow {\frac {1}{2}}(C_{Mi}^{j+1}+C_{Mi}^{j})。}$

7

ここで、代数を簡略化するために次の定数を作成します。

${\displaystyle \lambda ={\frac {D_{x}\,\Delta t}{2\,\Delta x^{2}}},}$

${\displaystyle \alpha ={\frac {U_{x}\,\Delta t}{4\,\Delta x}},}$

${\displaystyle \beta ={\frac {k\,\Delta t}{2}},}$

（2）, （3）, （4）, （5）, （6）, （7）,を（1 ）に代入する。そして、新しい時刻項を左辺（）に、現在の時刻項を右辺（） に代入して、${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \lambda }$ ${\displaystyle j+1}$ ${\displaystyle j}$

${\displaystyle -\beta C_{Ni}^{j+1}-(\lambda +\alpha )C_{i-1}^{j+1}+(1+2\lambda +2\beta )C_{i}^{j+1}-(\lambda -\alpha )C_{i+1}^{j+1}-\beta C_{Mi}^{j+1}={}}$

${\displaystyle \qquad \beta C_{Ni}^{j}+(\lambda +\alpha )C_{i-1}^{j}+(1-2\lambda -2\beta )C_{i}^{j}+(\lambda -\alpha )C_{i+1}^{j}+\beta C_{Mi}^{j}.}$

最初のチャネルをモデル化するには、次のチャネル（ ）とのみ接触できることが分かるので、式は次のように簡略化される。 ${\displaystyle M}$

${\displaystyle -(\lambda +\alpha )C_{i-1}^{j+1}+(1+2\lambda +\beta )C_{i}^{j+1}-(\lambda -\alpha )C_{i+1}^{j+1}-\beta C_{Mi}^{j+1}={}}$

${\displaystyle \qquad {}+(\lambda +\alpha )C_{i-1}^{j}+(1-2\lambda -\beta )C_{i}^{j}+(\lambda -\alpha )C_{i+1}^{j}+\beta C_{Mi}^{j}.}$

同様に、最後のチャネルをモデル化するには、それが前のチャネル（ ）とのみ接触できることに気づくので、式は次のように簡略化されます。 ${\displaystyle N}$

${\displaystyle -\beta C_{Ni}^{j+1}-(\lambda +\alpha )C_{i-1}^{j+1}+(1+2\lambda +\beta )C_{i}^{j+1}-(\lambda -\alpha )C_{i+1}^{j+1}={}}$

${\displaystyle \qquad \beta C_{Ni}^{j}+(\lambda +\alpha )C_{i-1}^{j}+(1-2\lambda -\beta )C_{i}^{j}+(\lambda -\alpha )C_{i+1}^{j}.}$

この線形方程式を解くには、まずチャネルの先頭に境界条件を与える必要があることがわかります。

${\displaystyle C_{0}^{j}}$ : 現在の時間ステップにおけるチャネルの境界条件、

${\displaystyle C_{0}^{j+1}}$ : 次の時間ステップにおけるチャネルの境界条件、

${\displaystyle C_{N0}^{j}}$ : 前のチャネルから現在の時間ステップで解析されたチャネルまでの境界条件、

${\displaystyle C_{M0}^{j}}$ : 現在の時間ステップで解析されたチャネルの次のチャネルの境界条件。

チャネルの最後のセル（）では、最も都合の良い条件は断熱条件となるので、 ${\displaystyle z}$

${\displaystyle \left.{\frac {\partial C}{\partial x}}\right|_{x=z}={\frac {C_{i+1}-C_{i-1}}{2\,\Delta x}}=0.}$

この条件は、（ヌル値に関係なく）次の場合にのみ満たされます。

${\displaystyle C_{i+1}^{j+1}=C_{i-1}^{j+1}.}$

3チャネル、5ノード（初期境界条件を含む）の場合について、この問題を（行列形式で）解いてみましょう。これを線形システム問題として表現します。

${\displaystyle \mathbf {AA} \,\mathbf {C^{j+1}} =\mathbf {BB} \,\mathbf {C^{j}} +\mathbf {d} ,}$

どこ

${\displaystyle \mathbf {C^{j+1}} ={\begin{bmatrix}C_{11}^{j+1}\\C_{12}^{j+1}\\C_{13}^{j+1}\\C_{14}^{j+1}\\C_{21}^{j+1}\\C_{22}^{j+1}\\C_{23}^{j+1}\\C_{24}^{j+1}\\C_{31}^{j+1}\\C_{32}^{j+1}\\C_{33}^{j+1}\\C_{34}^{j+1}\end{bmatrix}},\quad \mathbf {C^{j}} ={\begin{bmatrix}C_{11}^{j}\\C_{12}^{j}\\C_{13}^{j}\\C_{14}^{j}\\C_{21}^{j}\\C_{22}^{j}\\C_{23}^{j}\\C_{24}^{j}\\C_{31}^{j}\\C_{32}^{j}\\C_{33}^{j}\\C_{34}^{j}\end{bmatrix}}.}$

ここで、 AAとBB は4 つの異なるサブ配列で構成される配列である必要があることを認識する必要があります(この例では 3 つのチャネルのみが考慮されていますが、これは上記で説明した主要部分をカバーしていることに注意してください)。

${\displaystyle \mathbf {AA} ={\begin{bmatrix}AA1&AA3&0\\AA3&AA2&AA3\\0&AA3&AA1\end{bmatrix}},\quad \mathbf {BB} ={\begin{bmatrix}BB1&-AA3&0\\-AA3&BB2&-AA3\\0&-AA3&BB1\end{bmatrix}},}$

上記の要素は次の配列に対応し、さらにゼロで満たされた4×4の配列が追加されます。AAとBBのサイズは12×12であることに注意してください。

${\displaystyle \mathbf {AA1} ={\begin{bmatrix}(1+2\lambda +\beta )&-(\lambda -\alpha )&0&0\\-(\lambda +\alpha )&(1+2\lambda +\beta )&-(\lambda -\alpha )&0\\0&-(\lambda +\alpha )&(1+2\lambda +\beta )&-(\lambda -\alpha )\\0&0&-2\lambda &(1+2\lambda +\beta )\end{bmatrix}},}$

${\displaystyle \mathbf {AA2} ={\begin{bmatrix}(1+2\lambda +2\beta )&-(\lambda -\alpha )&0&0\\-(\lambda +\alpha )&(1+2\lambda +2\beta )&-(\lambda -\alpha )&0\\0&-(\lambda +\alpha )&(1+2\lambda +2\beta )&-(\lambda -\alpha )\\0&0&-2\lambda &(1+2\lambda +2\beta )\end{bmatrix}},}$

${\displaystyle \mathbf {AA3} ={\begin{bmatrix}-\beta &0&0&0\\0&-\beta &0&0\\0&0&-\beta &0\\0&0&0&-\beta \end{bmatrix}},}$

${\displaystyle \mathbf {BB1} ={\begin{bmatrix}(1-2\lambda -\beta )&(\lambda -\alpha )&0&0\\(\lambda +\alpha )&(1-2\lambda -\beta )&(\lambda -\alpha )&0\\0&(\lambda +\alpha )&(1-2\lambda -\beta )&(\lambda -\alpha )\\0&0&2\lambda &(1-2\lambda -\beta )\end{bmatrix}},}$

${\displaystyle \mathbf {BB2} ={\begin{bmatrix}(1-2\lambda -2\beta )&(\lambda -\alpha )&0&0\\(\lambda +\alpha )&(1-2\lambda -2\beta )&(\lambda -\alpha )&0\\0&(\lambda +\alpha )&(1-2\lambda -2\beta )&(\lambda -\alpha )\\0&0&2\lambda &(1-2\lambda -2\beta )\end{bmatrix}}.}$

ここでのdベクトルは境界条件を保持するために使用されます。この例では12×1ベクトルです。

${\displaystyle \mathbf {d} ={\begin{bmatrix}(\lambda +\alpha )(C_{10}^{j+1}+C_{10}^{j})\\0\\0\\0\\(\lambda +\alpha )(C_{20}^{j+1}+C_{20}^{j})\\0\\0\\0\\(\lambda +\alpha )(C_{30}^{j+1}+C_{30}^{j})\\0\\0\\0\end{bmatrix}}.}$

任意の時点での濃度を求めるには、次の式を繰り返す必要があります。

${\displaystyle \mathbf {C^{j+1}} =\mathbf {AA} ^{-1}(\mathbf {BB} \,\mathbf {C^{j}} +\mathbf {d} ).}$

例: 2D拡散

均一な直交座標格子上の2次元に拡張する場合も、導出は同様であり、結果は三重対角方程式ではなく帯対角方程式の系となる可能性がある。2次元熱方程式は

${\displaystyle {\frac {\partial u}{\partial t}}=a\,\nabla ^{2}u,}$

${\displaystyle {\frac {\partial u}{\partial t}}=a\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\right)}$

は、クランク・ニコルソン離散化によって解くことができる。

${\displaystyle {\begin{aligned}u_{i,j}^{n+1}={}&u_{i,j}^{n}+{\frac {1}{2}}{\frac {a\Delta t}{(\Delta x)^{2}}}{\big [}(u_{i+1,j}^{n+1}+u_{i-1,j}^{n+1}+u_{i,j+1}^{n+1}+u_{i,j-1}^{n+1}-4u_{i,j}^{n+1})\\&+(u_{i+1,j}^{n}+u_{i-1,j}^{n}+u_{i,j+1}^{n}+u_{i,j-1}^{n}-4u_{i,j}^{n}){\big ]},\end{aligned}}}$

正方格子が使用されると仮定すると、 となる。この式は、項を並べ替え、 CFL数を使用することでいくらか簡略化できる。${\displaystyle \Delta x=\Delta y}$

${\displaystyle \mu ={\frac {a\,\Delta t}{(\Delta x)^{2}}}.}$

クランク・ニコルソン数値計算法では、CFL数が小さいことは安定性には必要ではないが、数値精度には必要である。この計算法は次のように書ける。

${\displaystyle (1+2\mu )u_{i,j}^{n+1}-{\frac {\mu }{2}}\left(u_{i+1,j}^{n+1}+u_{i-1,j}^{n+1}+u_{i,j+1}^{n+1}+u_{i,j-1}^{n+1}\right)}$

${\displaystyle \qquad =(1-2\mu )u_{i,j}^{n}+{\frac {\mu }{2}}\left(u_{i+1,j}^{n}+u_{i-1,j}^{n}+u_{i,j+1}^{n}+u_{i,j-1}^{n}\right).}$

このような線形システムを解くのはコストがかかる。そのため、数値偏微分方程式を解くために、交互方向陰解法を実装することができる。この場合、一方の次元は暗黙的に扱い、もう一方の次元は割り当てられた時間ステップの半分については明示的に扱い、残りの半分についてはその逆の処理を行う。この戦略の利点は、陰解法では三角行列アルゴリズムのみを解くだけで済むことである。真のクランク・ニコルソン解とADI近似解の精度の差は オーダーであり、したがって十分に小さい時間ステップであれば無視できる。^{[ 4 ]}${\displaystyle O(\Delta t^{4})}$

非線形問題に対するクランク・ニコルソン

クランク・ニコルソン法は暗黙的なため、一般に厳密な解を得ることは不可能です。解に収束させるためには、反復法を用いるべきです。ニュートン法を用いて予測値を収束させるという選択肢もありますが、これにはヤコビアンを計算する必要があります。数値流体力学や数値相対論のような高次元系では、このヤコビアンを計算することは不可能な場合があります。

ヤコビアンフリーの代替法として、固定点反復法があります。 がシステムの速度である場合、クランク・ニコルソン予測は写像の固定点になります。写像反復法が収束しない場合は、 をパラメータ化した写像 （ ）の方が挙動が良好になる可能性があります。展開された形では、更新式は次のようになります。 ${\displaystyle f}$ ${\displaystyle \Phi (x)=x_{0}+{\frac {h}{2}}\left[f(x_{0})+f(x)\right].}$ ${\displaystyle x^{(i+1)}=\Phi (x^{(i)})}$ ${\displaystyle \Theta (x,\alpha )=\alpha x+(1-\alpha )\Phi (x)}$ ${\displaystyle \alpha \in (0,1)}$

${\displaystyle x^{i+1}=\alpha x^{i}+(1-\alpha )\left[x_{0}+{\frac {h}{2}}\left(f(x_{0})+f(x^{i})\right)\right],}$

ここで、 は現在の推定値であり、は前のタイムステップです。 ${\displaystyle x^{i}}$ ${\displaystyle x_{i-1}}$

高次元システムの場合でも、このマップの反復は驚くほど速く収束します。

渦度形式におけるナビエ・ストークス方程式の数値解。この場合、クランク・ニコルソン法の固定点反復法を収束させるのに必要であった。${\displaystyle \alpha =7/8}$

金融数学への応用

熱方程式（金融数学では拡散方程式と呼ばれることが多い）を用いて他の多くの現象をモデル化できるため、クランク・ニコルソン法はそれらの分野にも適用されてきた。^{[ 5 ]}特に、ブラック・ショールズ・オプション価格設定モデルの微分方程式は熱方程式に変換できるため、 クランク・ニコルソン法を用いてオプション価格設定の数値解を得ることができる。

金融におけるこの重要性は、オプション価格設定問題が標準的な仮定を超えて拡張された場合（例えば、配当金の変動を組み込んだ場合）、閉形式では解くことができないが、この手法を用いることで解けるという点にある。しかし、最終条件が滑らかでない場合（ほとんどの金融商品で発生する）、数値振動が抑制されないため、クランク・ニコルソン法は不十分である。バニラオプションの場合、これは行使価格付近でガンマ値の振動を引き起こす。したがって、特別な減衰初期化手順（例えば、完全暗黙差分法）が必要となる。

参照

• 金融数学
• 台形則

参考文献

1. タンサー・セベシ (2002)。対流熱伝達。スプリンガー。ISBN 0-9668461-4-1。
2. Crank, J. ; Nicolson, P. (1947). 「熱伝導型偏微分方程式の解の数値的評価のための実用的手法」.ケンブリッジ哲学協会数学紀要. 43 (1): 50– 67. Bibcode : 1947PCPS...43...50C . doi : 10.1017/S0305004100023197 . S2CID 16676040 . 
3. Thomas, JW (1995).数値偏微分方程式：有限差分法. 応用数学テキスト. 第22巻. ベルリン、ニューヨーク: Springer-Verlag . ISBN 978-0-387-97999-1。例3.3.2は、Crank-Nicolsonが に適用された場合に無条件に安定であることを示しています。${\displaystyle u_{t}=au_{xx}}$
4. 「多次元放物型問題」（PDF） .コンピュータサイエンス学科. RPI . 2016年5月29日閲覧。
5. Wilmott, P.; Howison, S.; Dewynne, J. (1995). 『金融デリバティブの数学：学生のための入門』ケンブリッジ大学出版局. ISBN 0-521-49789-2金融デリバティブの数学 ウィルモット。

外部リンク

• 科学者とエンジニアのための数値偏微分方程式テクニック、オープンアクセスの数値偏微分方程式の講義とコード
• 移流方程式にクランク・ニコルソン法を適用し実装する方法の例