散逸ソリトン

散逸ソリトン（DS ）は、非線形空間的に拡張された散逸系において自己組織化のメカニズムによって生じる安定な孤立局在構造（ソリトン）である。これらは、保存系における古典的なソリトン概念の拡張と考えることができる。別名として、オートソリトン、スポット、パルスなどがある。

束縛状態の形成といった古典粒子の挙動に類似した側面に加え、DSはエネルギー保存則や運動量保存則の制約を受けずに、散乱、生成、消滅といった興味深い挙動を示す。内部自由度の励起により、動的に安定化された固有速度、あるいは形状の周期的な振動が生じる可能性がある。

歴史的発展

ソリトン概念の起源

DSは古くから実験的に観測されてきました。 ヘルムホルツ^{[ 1 ]}は1850年に神経パルスの伝播速度を測定しました。1902年にはレーマン^{[ 2 ]}が長いガス放電管に局所的な陽極点が形成されることを発見しました。しかし、「ソリトン」という用語はもともと別の文脈で生まれました。その出発点は、1834年にラッセルが「孤立水波」を実験的に検出したことでした。 ^{[ 3 ]} これらの観察は、 1870年頃にレイリー^{[ 4 ]}とブシネスク^{[ 5 ]}による理論的研究のきっかけとなり、最終的に1895年にコルテウェグとド・フリースによってそのような波の近似的な記述が示されました。この記述は今日、（保存則的な） KdV方程式として知られています 。^{[ 6 ]}

このような背景から、1965年にザブスキーとクラスカル^{[ 7 ]}によって「ソリトン」という用語が造語されました。彼らはKdV方程式のよく局所化された孤立解を研究し、これらの物体をソリトンと名付けました。彼らは特に、1次元空間にソリトンが存在することを実証しました。例えば、ソリトンは2つの異なるサイズと速度を持つ一方向に伝播するパルスの形で存在し、衝突前後で数、形状、サイズが同じであるという注目すべき特性を示します。

ガードナーら^{[ 8 ]}は KdV方程式を解くための 逆散乱法を導入し、この方程式が完全に積分可能であることを証明した。1972年にザカロフとシャバット^{[ 9 ]}は別の積分可能な方程式を発見し、最終的に逆散乱法が方程式の全クラス（例えば 非線形シュレーディンガー方程式や サイン・ゴルドン方程式）に適用可能であることが証明された。1965年から1975年頃にかけて、ソリトンという用語を、逆散乱法を用いて解ける保存的非線形偏微分方程式のパルス状孤立解にのみ用いるという共通の合意が得られた。

弱散逸系と強散逸系

古典ソリトンに関する知識が増えるにつれて、技術的な応用の可能性が見えてきた。現在最も有望視されているのは、データ伝送を目的とした ガラスファイバーを介した光ソリトンの伝送である。保存システムとは対照的に、ファイバー内のソリトンはエネルギーを散逸し、これは中時間および長時間スケールでは無視できない。しかし、古典ソリトンの概念は、短時間スケールではエネルギーの散逸を無視できるという意味で依然として使用できる。中時間スケールでは小さなエネルギー損失を摂動として考慮する必要があり、長時間スケールではソリトンの振幅は減衰し、最終的には消滅する。^{[ 10 ]}

しかしながら、孤立構造を生成でき、その形成と安定化に散逸が重要な役割を果たす様々なタイプのシステムが存在する。これらのDSの特定のタイプに関する研究は長年行われてきたが（例えば、1952年のホジキンとハクスリーの研究で最高潮に達した神経パルスの研究を参照）、1990年以降、研究量は大幅に増加した（例えば、^[ 12 ^{] [} 13 ] [ 14 ] [ 15 ] を参照^{）。考えられる理由としては、実験装置と解析}技術の改善、および数値計算用のより強力なコンピュータの利用可能性が挙げられる。今日では、強い散逸システムの孤立構造に対して散逸ソリトンという用語を使用するのが一般的である。

実験観察

今日、DSは様々な実験装置で使用されています。例としては、

• ガス放電システム：放電空間に閉じ込められたプラズマ。この空間は主放電長に比べて横方向に長いことが多い。DSは電極間の電流フィラメントとして発生し、高抵抗バリアを備えたDCシステム^{[ 16 ]} 、誘電体バリアを備えたACシステム^{[ 17 ]}、陽極スポット^{[ 18 ]}、金属電極を備えた遮蔽放電^{[ 19 ]で見られる。}

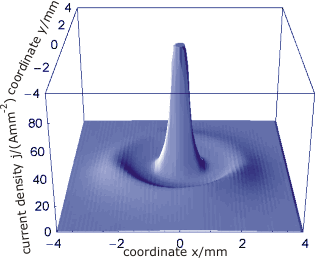
• 高抵抗障壁を有する平面直流ガス放電システムで実験的に観測されたDS
• 
  振動テールのない平均電流密度分布。
• 
  振動する裾を持つ平均電流密度分布。

• 半導体システム：ガス放電に似ていますが、ガスの代わりに半導体材料が2つの平面または球状の電極の間に挟まれています。例としては、SiおよびGaAsのpinダイオード^{[ 20 ]}、n-GaAs ^{[ 21 ]}、Siのp ⁺ −n ⁺ −p−n ^{− [ 22 ]}、ZnS:Mn構造などがあります。^{[ 23 ]}
• 非線形光学システム：高強度光線が非線形媒質と相互作用する。典型的には、媒質は光線の伝播時間に比べてかなり遅い時間スケールで反応する。多くの場合、出力は単一ミラーフィードバックまたはフィードバックループを介して入力システムにフィードバックされる。DSは、光線の伝播方向に直交する2次元平面上の明るい点として発生することがあるが、偏光などの他の効果を利用することもできる。DSは、飽和吸収体^{[ 24 ]}、 [ ²⁵ ]縮退光パラメトリック発振器（DOPO）^{[ 26 ]}液晶ライトバルブ（LCLV）^{[ 27 ]}アルカリ蒸気システム^{[ 28 ]}フォトリフラクティブ媒質[ ^{29 ]および半導体微小共振器[ 29 ]で観測されている}。
• DSのベクトル特性を考慮すると、ベクトル散逸ソリトンは、飽和吸収体を介して受動モード同期されたファイバーレーザーでも観測される可能性がある^{[ 30 ]。}
• さらに、SESAMを用いて受動モード同期された全正常分散光ファイバレーザーにおいて、多波長散逸ソリトンが観測された。共振器の複屈折に依存して、レーザー内で安定な単波長、二波長、三波長散逸ソリトンが形成されることが確認された。その発生メカニズムは、散逸ソリトンの性質に遡ることができる。^{[ 31 ]}
• 化学システム：一次元または二次元反応器、あるいは触媒表面を介して実現されるDSは、濃度または温度の上昇を伴うパルス（多くの場合、伝播するパルス）として現れる。代表的な反応としては、ベロウソフ・ジャボチンスキー反応^{[ 32 ]}、フェ^{ロシアン化物・ヨウ素酸・亜硫酸塩反応、水素[ 33 ]}、CO ^{[ 34 ] 、鉄[ 35} ]の酸化反応などがある。神経パルス^{[ 11 ]}や片頭痛のオーラ波^{[ 36 ]}もこのクラスのシステムに属する。
• 振動媒体：垂直に振られた粒状媒体^{[ 37 ]} 、コロイド懸濁液^{[ 38 ]}、ニュートン流体^{[ 39 ]}は、調和的または低調和的に振動する物質の塊を生成し、これは通常オシロンと呼ばれます。
• 流体力学システム：DSの最も顕著な実現例は、二成分液体中の伝導背景状態における対流ロールの領域である。 ^{[ 40 ]}もう1つの例は、油で満たされた回転円筒管内を引きずる膜である。^{[ 41 ]}
• 電気ネットワーク：非線形の電流-電圧特性を持つ結合した細胞の大規模な1次元または2次元配列。^{[ 42 ]} DSは細胞を流れる電流が局所的に増加することを特徴とします。

驚くべきことに、上記の多くの系におけるDSのダイナミクスは、微視的な違いにもかかわらず、現象論的には類似しています。典型的な観察例としては、（固有の）伝播、散乱、束縛状態およびクラスターの形成、勾配のドリフト、相互浸透、生成、消滅、そして高次不安定性などが挙げられます。

理論的説明

DSを示すシステムのほとんどは、非線形偏微分方程式によって記述されます 。離散差分方程式や セルオートマトンも用いられます。これまで、第一原理に基づくモデリングとそれに続く実験と理論の定量的な比較はほとんど行われておらず、微視的および巨視的な時間・空間スケール間の大きな乖離のために深刻な問題を引き起こすこともあります。多くの場合、より大規模な実験システムにおける本質的な物理過程を反映した、簡略化されたプロトタイプモデルが研究されています。これらの中には、

• 反応拡散系は化学システム、ガス放電、半導体などに用いられる。^{[ 43 ]}異なる反応物の濃度を表す状態ベクトルq ( x ,  t )の変化は、拡散と局所反応によって決定される。

${\displaystyle \partial _{t}{\boldsymbol {q}}={\underline {\boldsymbol {D}}}\,\Delta {\boldsymbol {q}}+{\boldsymbol {R}}({\boldsymbol {q}}).}$

よく見られる例としては、2成分のフィッツヒュー・ナグモ型活性剤・阻害薬システムが挙げられる。

${\displaystyle \left({\begin{array}{c}\tau _{u}\,\partial _{t}u\\\tau _{v}\,\partial _{t}v\end{array}}\right)=\left({\begin{array}{cc}d_{u}^{2}&0\\0&d_{v}^{2}\end{array}}\right)\left({\begin{array}{c}\Delta u\\\Delta v\end{array}}\right)+\left({\begin{array}{c}\lambda uu^{3}-\kappa _{3}v+\kappa _{1}\\uv\end{array}}\right).}$

定常DSは、DS中心部での物質生成、尾部への拡散輸送、そして尾部における物質の減少によって生成される。伝播するパルスは、先端部での生成と後端での減少によって生じる。^{[ 44 ]}その他の効果としては、DSの周期的な振動（「ブリージング」）^{[ 45 ] [ 46 ]}束縛状態^{[ 47 ]}衝突、合体、生成、消滅^{[ 48 ]などが見られる。}

• 複素スカラーq ( x ,  t )に対するギンツブルグ・ランダウ型方程式は、非線形光学系、プラズマ、ボーズ・アインシュタイン凝縮、液晶、粒状媒体などを記述するために使用される。^{[ 49 ]}よく見られる例としては、三次五次亜臨界ギンツブルグ・ランダウ方程式がある。

${\displaystyle \partial_{t}q=(d_{r}+id_{i})\,\Delta q+\ell_{r}q+(c_{r}+ic_{i})|q|^{2}q+(q_{r}+iq_{i})|q|^{4}q.}$

DSの形成に至るメカニズムを理解するために、エネルギーρ = | q | ²を考慮すると、連続方程式を導くことができる。

${\displaystyle {\begin{aligned}&\partial _{t}\rho +\nabla \cdot {\boldsymbol {m}}=S=d_{r}(q\,\Delta q^{\ast }+q^{\ast }\,\Delta q)+2\ell _{r}\rho +2c_{r}\rho ^{2}+2q_{r}\rho ^{3}\\&{\text{with }}{\boldsymbol {m}}=2d_{i}\operatorname {Im} (q^{\ast }\nabla q).\end{aligned}}}$

これにより、エネルギーは一般的にDSの側面で生成され、中心へ輸送され、場合によっては尾部へ輸送されてそこで枯渇することがわかる。力学現象としては、1次元で伝播するDS ^{[ 50 ]} 、 2次元で伝播するクラスター^{[ 51 ]} 、束縛状態と渦ソリトン^{[ 52 ]} 、そして「爆発するDS」^{[ 53 ]などが挙げられる。}

• スウィフト・ホーエンベルグ方程式は、非線形光学、および炎や電気対流などの粒状媒質の力学において用いられる。スウィフト・ホーエンベルグ方程式は、ギンツブルグ・ランダウ方程式の拡張とみなすことができる。これは次のように書ける。

${\displaystyle \partial_{t}q=(s_{r}+is_{i})\,\Delta^{2}q+(d_{r}+id_{i})\,\Deltaq+\ell_{r}q+(c_{r}+ic_{i})|q|^{2}q+(q_{r}+iq_{i})|q|^{4}q.}$

d _r > 0の場合、本質的にはギンツブルグ・ランダウ方程式と同じメカニズムになります。^{[ 54 ]} d _r < 0の場合 、実スウィフト・ホーエンベルグ方程式では、同次状態とチューリングパターンの間に双安定性が見られます。DSは、同次背景上の定常で局所的なチューリング領域です。^{[ 55 ]}これは複素スウィフト・ホーエンベルグ方程式にも当てはまりますが、伝播するDSや相互作用現象も可能であり、合体や相互浸透が観測されます。^{[ 56 ]}

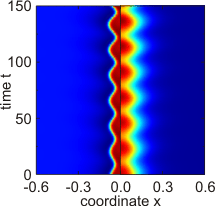
• 1つの空間次元における上記のモデル方程式の数値解としてDSのダイナミクスと相互作用を示す時空間プロット
• 
  活性剤u (左半分) と抑制剤v (右半分)を含む 2 成分反応拡散システムの溶液としての単一の「呼吸」 DS 。
• 
• 

粒子の性質と普遍性

様々な系における散逸ソリトンは、普遍的な粒子のような性質を示す。後者を理解し記述するためには、散逸ソリトンの位置、速度、振幅といったゆっくりと変化する秩序パラメータに対する「粒子方程式」を、場の記述におけるすべての高速変数を断熱的に消去することで導出することが考えられる。この手法は線形系では知られているが、非線形モデルでは高速モードと低速モードの結合により数学的な問題が生じる。^{[ 57 ]}

低次元の力学系と同様に、定常散逸ソリトンの超臨界分岐に対しては、本質的に系の対称性に依存する特徴的な正規形が見られる。例えば、対称的な定常散逸ソリトンから本質的に伝播する散逸ソリトンへの遷移に対しては、ピッチフォーク正規形が見られる。

${\displaystyle {\dot {\boldsymbol {v}}}=(\sigma -\sigma _{0}){\boldsymbol {v}}-|{\boldsymbol {v}}|^{2}{\boldsymbol {v}}}$

散逸ソリトンの速度vについて^{[ 58 ]} 、 σは分岐パラメータ、σ0は分岐点を表す_。 「呼吸する」散逸ソリトンへの分岐については、ホップ正規形が求められる。

${\displaystyle {\dot {A}}=(\sigma -\sigma _{0})A-|A|^{2}A}$

振動の振幅Aについてである。 ^{[ 46 ]} DSの重なりが大きすぎない限り、 「弱い相互作用」を扱うことも可能である。 ^{[ 59 ]}このようにして、実験と理論の比較が容易になる。^{[ 60 ] [ 61 ]} 逆散乱理論は完全な解析解を与えるため、上記の問題は古典ソリトンに対しては発生しないことに注意されたい。

参照

• クラポティス
• コンパクトサポートを持つソリトンであるコンパクトトン
• ファイバーレーザー
• 異常波は関連現象かもしれない
• グラフェン
• 非線形シュレーディンガー方程式
• 非線形システム
• オシロン
• 微分不可能なピークを持つソリトン、ピーコン
• Qボール、非位相的ソリトン
• サイン・ゴルドン方程式
• 離散媒質中の孤立波^{[ 62 ]}
• ソリトン（光学）
• ソリトン（位相的）
• 神経インパルス伝播のソリトンモデル
• 位相量子数
• ベクトルソリトン

参考文献

列をなして

1. ヘルムホルツ、H. (1850)。「ネルヴェンの中で、動物を攻撃する動物と死の要塞を守るための軍事行動」。解剖学、生理学、医学のアーカイブ(ドイツ語)。57：276
2. リーマン、O. (1902)。「Gasentladungen in weiten Gefässen」。Annalen der Physik (ドイツ語)。312 (1)。ワイリー: 1–28。土井: 10.1002/andp.19013120102。ISSN 0003-3804。 
3. JSラッセル、英国科学振興協会第14回会議報告書（1845年）：311
4. レイリー, JW (1876). 「XXXII. 波について」.ロンドン、エディンバラ、ダブリン哲学雑誌・科学ジャーナル. 1 (4). Informa UK Limited: 257– 279. doi : 10.1080/14786447608639037 . ISSN 1941-5982 . 
5. ブシネスク、J. (1871)。「流体力学 - ソリティアと翻訳による発光液体の理論、運河の長方形による宣伝」。Comptes rendus hebdomadaires des séances de l'Académie des Sciences (フランス語)。72：755
6. Korteweg, DJ; de Vries, G. (1895). 「XLI. 長方形の運河を進む長波の形状変化と新しいタイプの長定常波について」 .ロンドン、エディンバラ、ダブリン哲学雑誌・科学ジャーナル. 39 (240). Informa UK Limited: 422– 443. doi : 10.1080/14786449508620739 . ISSN 1941-5982 . 
7. Zabusky, NJ; Kruskal, MD (1965年8月9日). 「無衝突プラズマにおける「ソリトン」の相互作用と初期状態の再帰」 . Physical Review Letters . 15 (6). アメリカ物理学会: 240–243 . Bibcode : 1965PhRvL..15..240Z . doi : 10.1103/physrevlett.15.240 . ISSN 0031-9007 . 
8. Gardner, Clifford S.; Greene, John M.; Kruskal, Martin D.; Miura, Robert M. (1967年11月6日). 「Korteweg-de Vries方程式の解法」. Physical Review Letters . 19 (19). American Physical Society: 1095–1097 . Bibcode : 1967PhRvL..19.1095G . doi : 10.1103/physrevlett.19.1095 . ISSN 0031-9007 . 
9. Zakharov, VE; Shabat, AB (1975). 「逆散乱問題法による数理物理学の非線形方程式の積分法 I」.関数解析とその応用. 8 (3). Springer Science and Business Media: 226– 235. doi : 10.1007/bf01075696 . ISSN 0016-2663 . S2CID 120856178 .  
10. Kivshar, YS; Agrawal, GP (2003).光ソリトン：ファイバーからフォトニック結晶へ. アムステルダム・ボストン: アカデミック・プレス. ISBN 978-0-12-410590-4. OCLC  162129411 .
11. Hodgkin, AL; Huxley, AF (1952年8月28日). 「膜電流の定量的記述と神経伝導および興奮への応用」 . The Journal of Physiology . 117 (4). Wiley: 500–544 . doi : 10.1113/jphysiol.1952.sp004764 . ISSN 0022-3751 . PMC 1392413. PMID 12991237 .   
12. Kerner, BS; Osipov, VV (1994).オートソリトン：自己組織化と乱流の問題への新たなアプローチ. ドルドレヒト・ボストン: Kluwer Academic. p. 53. ISBN 978-0-7923-2816-2. OCLC  30157395 .
13. Bode, M.; Purwins, H.-G. (1995). 「反応拡散系におけるパターン形成 - 物理系における散逸ソリトン」. Physica D: 非線形現象. 86 ( 1– 2). Elsevier BV: 53– 63. Bibcode : 1995PhyD...86...53B . doi : 10.1016/0167-2789(95)00087-k . ISSN 0167-2789 . 
14. Christov, CI; Velarde, MG (1995). 「散逸ソリトン」. Physica D: 非線形現象. 86 ( 1– 2). Elsevier BV: 323– 347. Bibcode : 1995PhyD...86..323C . doi : 10.1016/0167-2789(95)00111-g . ISSN 0167-2789 . 
15. Akhmediev, Nail; Ankiewicz, Adrian 編 (2005).散逸ソリトン. 物理学講義ノート. 第661巻. ベルリン、ハイデルベルク: Springer Berlin Heidelberg. doi : 10.1007/b11728 . ISBN 978-3-540-23373-2. ISSN  0075-8450 . S2CID  218646243 .
16. Radehaus, Ch.; Dirksmeyer, T.; Willebrand, H.; Purwins, H.-G. (1987). 「高インピーダンス電極を用いたガス放電システムにおけるパターン形成」. Physics Letters A. 125 ( 2– 3 ). Elsevier BV: 92– 94. Bibcode : 1987PhLA..125...92R . doi : 10.1016/0375-9601(87)90128-9 . ISSN 0375-9601 . 
17. Brauer, I.; Bode, M.; Ammelt, E.; Purwins, H.-G. (2000年4月1日). 「周期駆動ガス放電システムにおける移動点対：相互作用による集団運動」. Physical Review Letters . 84 (18). American Physical Society: 4104– 4107. Bibcode : 2000PhRvL..84.4104B . doi : 10.1103/physrevlett.84.4104 . ISSN 0031-9007 . PMID 10990621 .  
18. Rubens, Sidney M.; Henderson, JE (1940年8月1日). 「グロー放電における陽極点の特性と機能」. Physical Review . 58 (5). アメリカ物理学会: 446–457 . Bibcode : 1940PhRv...58..446R . doi : 10.1103/physrev.58.446 . ISSN 0031-899X . 
19. 那須野 悟 (2003). 「発光ガス放電点の踊る「原子」と「分子」」.カオス：非線形科学の学際的ジャーナル. 13 (3). AIP Publishing: 1010– 1013. Bibcode : 2003Chaos..13.1010N . doi : 10.1063/1.1604271 . ISSN 1054-1500 . PMID 12946194 .  
20. Jäger, D.; Baumann, H.; Symanczyk, R. (1986). 「シリコンpinダイオードにおける電流フィラメント形成による空間構造の実験的観測」. Physics Letters A. 117 ( 3). Elsevier BV: 141– 144. Bibcode : 1986PhLA..117..141J . doi : 10.1016/0375-9601(86)90021-6 . ISSN 0375-9601 . 
21. メイヤー、KM;パリシ、J.ヒューベナー、RP (1988)。 「GaAsにおける自己生成多芯電流パターンのイメージング」。物理学のためのツァイシュリフト B。71 (2)。 Springer Science and Business Media: 171–178。Bibcode : 1988ZPhyB..71..171M。土井：10.1007/bf01312786。ISSN 0722-3277。S2CID 121227300。  
22. Niedernostheide, F.-J.; Arps, M.; Dohmen, R.; Willebrand, H.; Purwins, H.-G. (1992年6月1日). 「pnpn半導体デバイスにおける空間的および時空間的パターン」. Physica Status Solidi B (ドイツ語). 172 (1). Wiley: 249–266 . Bibcode : 1992PSSBR.172..249N . doi : 10.1002/pssb.2221720123 . ISSN 0370-1972 . 
23. Beale, Marc (1993). 「直流薄膜ZnS:Mnエレクトロルミネッセンスデバイスにおける均一かつフィラメント状の輸送」. Philosophical Magazine B. 68 ( 5). Informa UK Limited: 573– 594. Bibcode : 1993PMagB..68..573B . doi : 10.1080/13642819308220144 . ISSN 1364-2812 . 
24. Taranenko, VB; Staliunas, K.; Weiss, CO (1997年7月1日). 「空間ソリトンレーザー：自己像共振器内に飽和吸収体を有するレーザーの局所構造」. Physical Review A. 56 ( 2). American Physical Society: 1582–1591 . Bibcode : 1997PhRvA..56.1582T . doi : 10.1103/physreva.56.1582 . ISSN 1050-2947 . 
25. Taranenko, VB; Staliunas, K.; Weiss, CO (1998年9月14日). 「縮退光パラメトリック混合におけるパターン形成と局所構造」. Physical Review Letters . 81 (11). American Physical Society: 2236– 2239. Bibcode : 1998PhRvL..81.2236T . doi : 10.1103/physrevlett.81.2236 . ISSN 0031-9007 . 
26. Schreiber, A.; Thüring, B.; Kreuzer, M.; Tschudi, T. (1997). 「非線形光フィードバックシステムにおける孤立構造の実験的研究」. Optics Communications . 136 ( 5– 6). Elsevier BV: 415– 418. Bibcode : 1997OptCo.136..415S . doi : 10.1016/s0030-4018(96)00722-5 . ISSN 0030-4018 . 
27. Schäpers, B.; Feldmann, M.; Ackemann, T.; Lange, W. (2000年7月24日). 「光学パターン形成システムにおける局所構造の相互作用」. Physical Review Letters . 85 (4). American Physical Society: 748– 751. Bibcode : 2000PhRvL..85..748S . doi : 10.1103/physrevlett.85.748 . ISSN 0031-9007 . PMID 10991389 .  
28. Denz, Cornelia ; Schwab, Michael ; Weilnau, Carsten (2003).光屈折光学における横方向パターン形成. Springer Tracts in Modern Physics. 第188巻. ベルリン、ハイデルベルク: Springer Berlin Heidelberg. doi : 10.1007/b13583 . ISBN 978-3-540-02109-4. ISSN  0081-3869 .
29. バーランド、ステファン;トレディチェ、ホルヘ R.ブランビッラ、マッシモ。ルギアト、ルイージ A.バル、サルバドール。他。 （2002年）。 「半導体マイクロキャビティ内のピクセルとしてのキャビティソリトン」。自然。419 (6908)。 Springer Nature: 699– 702。Bibcode : 2002Natur.419..699B。土井：10.1038/nature01049。ISSN 0028-0836。PMID 12384692。S2CID 4404010。   
30. Zhang, H.; Tang, DY; Zhao, LM; Wu, X.; Tam, HY (2009年1月6日). 「正の正の空洞分散を持つ分散管理空洞ファイバーレーザーにおける散逸ベクトルソリトン」 . Optics Express . 17 (2). The Optical Society: 455–60 . Bibcode : 2009OExpr..17..455Z . doi : 10.1364/oe.17.000455 . ISSN 1094-4087 . PMID 19158858 .  
31. Zhang, H.; Tang, DY; Wu, X.; Zhao, LM (2009年7月20日). 「エルビウムドープファイバーレーザーの多波長散逸ソリトン動作」 . Optics Express . 17 (15). The Optical Society: 12692–7 . arXiv : 0907.1782 . Bibcode : 2009OExpr..1712692Z . doi : 10.1364/oe.17.012692 . ISSN 1094-4087 . PMID 19654674 .  
32. Hamik, Chad T.; Manz, Niklas; Steinbock, Oliver (2001). 「1,4-シクロヘキサンジオンとベロウソフ−ジャボチンスキー反応における異常分散と引力パルス相互作用†」. The Journal of Physical Chemistry A. 105 ( 25). American Chemical Society: 6144– 6153. doi : 10.1021/jp010270j . ISSN 1089-5639 . 
33. Lane, Samuel L.; Luss, Dan (1993年2月8日). 「ニッケルリングにおける水素酸化中の回転温度パルス」. Physical Review Letters . 70 (6). American Physical Society: 830– 832. Bibcode : 1993PhRvL..70..830L . doi : 10.1103/physrevlett.70.830 . ISSN 0031-9007 . PMID 10054214 .  
34. Rotermund, HH; Jakubith, S.; von Oertzen, A.; Ertl, G. (1991年6月10日). 「表面反応におけるソリトン」. Physical Review Letters . 66 (23). American Physical Society: 3083– 3086. Bibcode : 1991PhRvL..66.3083R . doi : 10.1103/physrevlett.66.3083 . ISSN 0031-9007 . PMID 10043694 .  
35. 鈴木 良治, 生物理学, 9 (1976): 115
36. Dahlem, Markus A.; Hadjikhani, Nouchine (2009年3月1日). Ben-Jacob, Eshel (編). 「片頭痛のオーラ：弱感受性皮質における粒子状波の退縮」 . PLOS ONE . 4 (4) e5007. Public Library of Science. Bibcode : 2009PLoSO...4.5007D . doi : 10.1371 / journal.pone.0005007 . ISSN 1932-6203 . PMC 2659426. PMID 19337363 .   
37. Umbanhowar, Paul B.; Melo, Francisco; Swinney, Harry L. (1996). 「垂直振動する顆粒層における局所励起」. Nature . 382 (6594). Springer Nature: 793– 796. Bibcode : 1996Natur.382..793U . doi : 10.1038/382793a0 . ISSN 0028-0836 . S2CID 4338010 .  
38. Lioubashevski, O.; Hamiel, Y.; Agnon, A.; Reches, Z.; Fineberg, J. (1999年10月18日). 「垂直振動コロイド懸濁液中の振動子と伝播する孤立波」. Physical Review Letters . 83 (16). American Physical Society: 3190– 3193. Bibcode : 1999PhRvL..83.3190L . doi : 10.1103/physrevlett.83.3190 . ISSN 0031-9007 . 
39. Lioubashevski, O.; Arbell, H.; Fineberg, J. (1996年5月20日). 「駆動表面波における散逸的孤立状態」. Physical Review Letters . 76 (21). American Physical Society: 3959– 3962. Bibcode : 1996PhRvL..76.3959L . doi : 10.1103/physrevlett.76.3959 . ISSN 0031-9007 . PMID 10061156 .  
40. Ahlers, Guenter (1991). 「パターン形成システムの実験」. Physica D: 非線形現象. 51 ( 1– 3). Elsevier BV: 421– 443. Bibcode : 1991PhyD...51..421A . doi : 10.1016/0167-2789(91)90249-9 . ISSN 0167-2789 . 
41. Melo, F.; Douady, S. (1993年11月15日). 「孤立波から時空間的間欠性による静的パターンへ」. Physical Review Letters . 71 (20). アメリカ物理学会: 3283–3286 . Bibcode : 1993PhRvL..71.3283M . doi : 10.1103/physrevlett.71.3283 . ISSN 0031-9007 . PMID 10054934 .  
42. J. Nagumo et al.、Proc.研究所ラジオエンジン。エレクトロ。 50 (1962): 2061
43. Purwins, H.-G.; Bödeker, HU; Liehr, AW (2004). 「反応拡散系における散逸ソリトン」.散逸ソリトン. 物理学講義ノート. 第661巻. ベルリン、ハイデルベルク: Springer Berlin Heidelberg. pp.  267– 308. doi : 10.1007/10928028_11 . ISBN 978-3-540-23373-2。
44. Meron, Ehud (1992). 「興奮性媒体におけるパターン形成」. Physics Reports . 218 (1). Elsevier BV: 1– 66. Bibcode : 1992PhR...218....1M . doi : 10.1016/0370-1573(92)90098-k . ISSN 0370-1573 . 
45. Niedernostheide, F.-J.; Dohmen, R.; Willebrand, H.; Schulze, H.-J.; Purwins, H.-G. (1992). 「特性電気特性を持つ非線形物理システムにおけるパターン形成」.非線形性と無秩序性. Springer Proceedings in Physics. 第67巻. ベルリン、ハイデルベルク: Springer Berlin Heidelberg. pp.  282– 309. doi : 10.1007/978-3-642-84774-5_29 . ISBN 978-3-642-84776-9. ISSN  0930-8989 .
46. Gurevich, SV; Amiranashvili, Sh.; Purwins, H.-G. (2006年11月1日). 「3成分反応拡散系における呼吸散逸ソリトン」. Physical Review E. 74 ( 6) 066201. アメリカ物理学会. Bibcode : 2006PhRvE..74f6201G . doi : 10.1103/physreve.74.066201 . ISSN 1539-3755 . PMID 17280133 .  
47. Or-Guil, Michal; G. Kevrekidis, Ioannis; Bär, Markus (2000). 「励起性媒質中のパルスの安定束縛状態」. Physica D: 非線形現象. 135 ( 1– 2). Elsevier BV: 154– 174. Bibcode : 2000PhyD..135..154O . doi : 10.1016/s0167-2789(99)00136-0 . ISSN 0167-2789 . 
48. Schenk, CP; Or-Guil, M.; Bode, M.; Purwins, H.-G. (1997年5月12日). 「二次元領域における三成分反応拡散系における相互作用パルス」. Physical Review Letters . 78 (19). American Physical Society: 3781– 3784. Bibcode : 1997PhRvL..78.3781S . doi : 10.1103/physrevlett.78.3781 . ISSN 0031-9007 . 
49. Aranson, Igor S.; Kramer, Lorenz (2002年2月4日). 「複素ギンツブルグ・ランダウ方程式の世界」. Reviews of Modern Physics . 74 (1). American Physical Society: 99–143 . arXiv : cond-mat/0106115 . Bibcode : 2002RvMP...74...99A . doi : 10.1103/revmodphys.74.99 . ISSN 0034-6861 . S2CID 53142414 .  
50. Afanasjev, VV; Akhmediev, N.; Soto-Crespo, JM (1996年1月1日). 「五次複素ギンツブルグ-ランダウ方程式の局所解の3つの形式」. Physical Review E. 53 ( 2). American Physical Society: 1931– 1939. Bibcode : 1996PhRvE..53.1931A . doi : 10.1103/physreve.53.1931 . hdl : 10261/60458 . ISSN 1063-651X . PMID 9964456 .  
51. Rosanov, NN; Fedorov, SV; Shatsev, AN (2006). 「弱結合二次元空洞ソリトンクラスターの運動」. Journal of Experimental and Theoretical Physics . 102 (4). Pleiades Publishing: 547– 555. Bibcode : 2006JETP..102..547R . doi : 10.1134/s1063776106040030 . ISSN 1063-7761 . S2CID 59290663 .  
52. Crasovan, L.-C.; Malomed, BA; Mihalache, D. (2000年12月20日). 「2次元ギンツブルグ-ランダウ方程式における安定な渦ソリトン」. Physical Review E. 63 ( 1) 016605. アメリカ物理学会. Bibcode : 2000PhRvE..63a6605C . doi : 10.1103/physreve.63.016605 . ISSN 1063-651X . PMID 11304376 .  
53. Soto-Crespo, JM; Akhmediev, N.; Ankiewicz, A. (2000年10月2日). 「散逸系における脈動ソリトン、クリーピングソリトン、および噴出ソリトン」. Physical Review Letters . 85 (14). American Physical Society: 2937–2940 . Bibcode : 2000PhRvL..85.2937S . doi : 10.1103/physrevlett.85.2937 . hdl : 10261/54305 . ISSN 0031-9007 . PMID 11005972 .  
54. Soto-Crespo, JM; Akhmediev, Nail (2002年12月18日). 「複素五次Swift-Hohenberg方程式でモデル化された受動モード同期レーザーにおける複合ソリトンと2パルス生成」. Physical Review E. 66 ( 6) 066610. アメリカ物理学会. Bibcode : 2002PhRvE..66f6610S . doi : 10.1103/physreve.66.066610 . hdl : 10261/60258 . ISSN 1063-651X . PMID 12513432 .  
55. 坂口秀次; Brand, Helmut R. (1996). 「五次スウィフト・ホーエンベルグ方程式の任意長さにおける安定な局所解」. Physica D: 非線形現象. 97 ( 1– 3). Elsevier BV: 274– 285. Bibcode : 1996PhyD...97..274S . doi : 10.1016/0167-2789(96)00077-2 . ISSN 0167-2789 . 
56. 坂口秀次; Brand, Helmut R. (1998). 「五次複素Swift-Hohenberg方程式の局所パターン」. Physica D: 非線形現象. 117 ( 1–4 ). Elsevier BV: 95–105 . Bibcode : 1998PhyD..117...95S . doi : 10.1016/s0167-2789(97)00310-2 . ISSN 0167-2789 . 
57. フリードリヒ、ルドルフ (2005). 「パターン形成理論における群論的手法」 .非線形および無秩序システムの集団ダイナミクス. ベルリン/ハイデルベルク: シュプリンガー・フェアラーク. pp.  61–84 . doi : 10.1007/3-540-26869-3_4 . ISBN 3-540-21383-X。
58. Bode, M (1997). 「不均一パラメータ分布を持つ反応拡散系におけるフロント分岐」. Physica D: 非線形現象. 106 ( 3–4 ). Elsevier BV: 270–286 . Bibcode : 1997PhyD..106..270B . doi : 10.1016/s0167-2789(97)00050-x . ISSN 0167-2789 . 
59. Bode, M.; Liehr, AW; Schenk, CP; Purwins, H.-G. (2002). 「散逸ソリトンの相互作用：三成分反応拡散系における局所構造の粒子状挙動」. Physica D: 非線形現象. 161 ( 1– 2). Elsevier BV: 45– 66. Bibcode : 2002PhyD..161...45B . doi : 10.1016/s0167-2789(01)00360-8 . ISSN 0167-2789 . 
60. Bödeker, HU; Röttger, MC; Liehr, AW; Frank, TD; Friedrich, R.; Purwins, H.-G. (2003年5月28日). 「平面ガス放電系における散逸ソリトンのノイズ被覆ドリフト分岐」. Physical Review E. 67 ( 5) 056220. アメリカ物理学会. Bibcode : 2003PhRvE..67e6220B . doi : 10.1103/physreve.67.056220 . ISSN 1063-651X . PMID 12786263 .  
61. Bödeker, HU; Liehr, AW; Frank, TD; Friedrich, R; Purwins, HG (2004年6月15日). 「散逸ソリトンの相互作用則の測定」 . New Journal of Physics . 6 (1). IOP Publishing: 62. Bibcode : 2004NJPh....6...62B . doi : 10.1088/1367-2630/6/1/062 . ISSN 1367-2630 . 
62. 「検出不可能な波を検出」 Live Science、2005年6月14日。

書籍と概要記事

• N. Akhmediev と A. Ankiewicz, Dissipative Solitons , Lecture Notes in Physics, Springer, Berlin (2005)
• N. Akhmediev と A. Ankiewicz,散逸ソリトン：光学から生物学・医学へ, Lecture Notes in Physics, Springer, Berlin (2008)
• H.-G. Purwins他, Advances in Physics 59 (2010): 485 doi : 10.1080/00018732.2010.498228
• AW Liehr:反応拡散系における散逸ソリトン。メカニズム、ダイナミクス、相互作用。Springer Synergeticsシリーズ第70巻、Springer、ベルリン・ハイデルベルク、2013年、ISBN 978-3-642-31250-2