心電図学の今後の課題

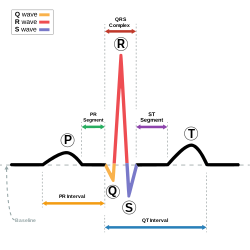
リアルな心拍のシミュレーション。

心電図で見た人間の心臓の正常な洞調律の模式図。

心電図学の前進課題は、体表面を通して心臓の電気的活動を研究するための計算的かつ数学的なアプローチである。 ^{[ 1 ]}この研究の主な目的は、虚血や心筋梗塞などの心臓病変の診断や医薬品介入の試験において重要な臨床的意義を持つ心電図（ECG）を計算的に再現することである。その重要な機能と比較的小さい侵襲性を考慮すると、心電図検査法は臨床診断検査として頻繁に利用されている。したがって、体内の心臓の挙動を数学的にモデル化することを意味するECGを計算的に再現することに進むのは自然な流れである。^{[ 1 ]}

ECG のフォワード モデルの 3 つの主要部分は次のとおりです。

• 心臓の電気活動のモデル。
• 心臓外領域を表す胴体内部の電位の拡散のモデル。
• いくつかの特定の心臓と胴体の結合状態。^{[ 2 ]}

したがって、心電図を得るためには、数学的な心臓電気モデルと、体幹部内の電気伝播を記述する受動導体内の拡散モデルを組み合わせる必要がある。^{[ 1 ]}

結合モデルは通常、偏微分方程式で表される3次元モデルです。このようなモデルは、解の空間発展については有限要素法、解の時間発展については有限差分法を含む半暗黙的数値スキームを用いて解かれます。しかし、このような手法、特に3次元シミュレーションでは、計算コストが非常に高くなります。そのため、例えば心臓の電気活動を胴体の問題とは独立して解くような簡略化されたモデルがしばしば検討されます。現実的な結果を得るためには、心臓と胴体の3次元解剖学的にリアルなモデルを使用する必要があります。^{[ 1 ]}

もう一つの単純化の方法は、 3つの常微分方程式からなる動的モデルである。^{[ 3 ]}

心臓組織モデル

心臓の電気的活動は、細胞膜を横切るイオンの流れ、すなわち細胞内と細胞外の空間間のイオンの流れによって引き起こされ、心筋に沿って興奮波が形成され、それが心臓の収縮と、循環器系を通して血液を送り出す心臓のポンプ作用を調整します。したがって、心臓の電気的活動のモデル化は、微視的レベルでのイオンの流れのモデル化と、巨視的レベルでの筋線維に沿った興奮波の伝播のモデル化に関連しています。^{[ 1 ] [ 4 ]}

マクロレベルの数学モデルにおいては、ウィレム・アイントホーフェンとアウグストゥス・ワラーが、固定点の周りを回転する双極子の概念モデルを用いて心電図を定義し、その誘導軸への投影によって誘導記録が決定された。その後、アイントホーフェンの四肢誘導I、II、IIIを理論的根拠として、前額面における心臓活動の2次元再構成が可能になった。 ^{[ 5 ]} その後、回転する心臓双極子は不十分とみなされ、胴体の境界領域内を移動する多極音源に置き換えられた。これらの音源を定量化する手法の主な欠点は、詳細が欠如していることであるが、心臓現象を現実的にシミュレートする上で非常に重要である。^{[ 4 ]}

一方、ミクロモデルは、単一細胞の挙動を表現し、それらの電気的特性を考慮してそれらを接続しようとする。^{[ 6 ] [ 7 ] [ 8 ]}これらのモデルは、特に再突入や体表面電位などの大規模な現象では、細胞の集合的な挙動が個々の細胞の挙動よりも重要であることを考慮すると、捉えるべき異なるスケールに関連したいくつかの課題を提示する。^{[ 4 ]}

心臓の電気活動をモデル化する3つ目の選択肢は、いわゆる「ミドルアウト・アプローチ」です。これは、モデルに低レベルの詳細と高レベルの詳細の両方を組み込むアプローチです。このオプションでは、連続体セルと呼ばれるセルブロックの挙動を考慮するため、スケールや詳細に関する問題を回避できます。得られたモデルはバイドメインモデルと呼ばれ、しばしばその簡略化であるモノドメインモデルに置き換えられます。^{[ 4 ]}

バイドメインモデル

心電図の順問題で考慮される領域と表記法を記述した、人間の胴体の様式化された表現。心臓とその周囲の人間の胴体を表す2つの分離された領域とその境界が考慮されている。

二領域モデルの基本的な仮定は、心臓組織が2つの抵抗性導電連続媒体に分割され、細胞膜を介して互いに接続されているものの分離されているというものである。これらの媒体は細胞内領域と細胞外領域と呼ばれ、前者は細胞組織、後者は細胞間の空間を表す。^{[ 2 ] [ 1 ]}

イオン電流の動的モデルを含むバイドメインモデルの標準的な定式化は、以下の通りである^{[ 2 ]。} ここで、およびはそれぞれ膜電位と細胞外電位、 はイオン電流であり、これはいわゆるゲーティング変数（細胞レベルのイオン挙動を考慮）にも依存する。はドメインに印加される外部電流である。さらに、およびは細胞内および細胞外の導電テンソル、は細胞膜の表面積と体積の比、は単位面積あたりの膜容量である。ここで、ドメインは心筋を表す^{[ 2 ] 。}$${\displaystyle {\begin{cases}\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla u_{e})=A_{m}\left(C_{m}{\dfrac {\partial V_{m}}{\partial t}}+I_{\text{ion}}(V_{m},w)\right)+I_{\text{app}}&{\text{in }}\Omega _{H}\\\nabla \cdot \left(({\boldsymbol {\sigma }}_{i}+{\boldsymbol {\sigma }}_{e})\nabla u_{e}\right)+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})=0&{\text{in }}\Omega _{H}\\{\frac {\partial w}{\partial {t}}}+g(V_{m},w)=0&{\text{in }}\Omega _{H}\end{cases}}}$$ ${\displaystyle V_{m}}$ ${\displaystyle u_{e}}$ ${\displaystyle I_{\text{イオン}}}$ ${\displaystyle w}$ ${\displaystyle I_{\text{app}}}$ ${\displaystyle {\boldsymbol {\sigma }}_{i}}$ ${\displaystyle {\boldsymbol {\sigma }}_{e}}$ ${\displaystyle A_{m}}$ ${\displaystyle C_{m}}$ ${\displaystyle \Omega _{H}}$

このバージョンのバイドメインモデルの境界条件は、心臓の外側に細胞内電位の流れがないという仮定によって得られます。つまり、 は 心臓領域の境界を表し、は の外向きの単位法線です。^{[ 2 ]}$${\displaystyle {\boldsymbol {\sigma }}_{i}\nabla V_{m}\cdot \mathbf {n} +{\boldsymbol {\sigma }}_{i}\nabla u_{e}\cdot \mathbf {n} =0\quad \quad {\text{on }}\Sigma }$$ ${\displaystyle \Sigma =\partial \Omega _{H}}$ ${\displaystyle \mathbf {n} }$ ${\displaystyle \Sigma }$

モノドメインモデル

モノドメインモデルは、いくつかの非生理学的な仮定にもかかわらず、少なくとも膜電位に関しては現実的な電気生理学的現象を表現できるバイドメインモデルを単純化したものである。^{[ 2 ] [ 1 ]}${\displaystyle V_{m}}$

標準的な定式化は次の偏微分方程式であり、その唯一の未知数は膜電位である。 ここで、は細胞内と細胞外の導電テンソルを関連付けるパラメータである。^{[ 2 ]}${\displaystyle V_{m}}$ $${\displaystyle \chi C_{m}{\frac {\partial V_{m}}{\partial t}}-\nabla \cdot \left({\boldsymbol {\sigma }}_{i}{\frac {\lambda }{1+\lambda }}\nabla V_{m}\right)+\chi I_{\text{ion}}=I_{\text{app}}\quad \quad {\text{in }}\Omega _{H}}$$ ${\displaystyle \lambda }$

このモデルに用いられる境界条件は^{[ 9 ]である。}$${\displaystyle \left({\boldsymbol {\sigma }}_{i}\nabla V_{m}\right)\cdot \mathbf {n} =0\quad \quad {\text{on }}\partial \Omega _{H}.}$$

胴体組織モデル

心電図の順問題では、胴体は受動導体とみなされ、そのモデルは準静的仮定の下でマクスウェル方程式から導くことができる。 ^{[ 1 ] [ 2 ]}

標準的な定式化は、1つの未知スカラー場、すなわち胴体電位を含む偏微分方程式で構成される。基本的に、胴体モデルは次の一般化ラプラス方程式で表される。 ここで、は導電率テンソル、は心臓、すなわち人間の胴体を囲む領域である。^{[ 2 ]}${\displaystyle u_{T}}$ $${\displaystyle \nabla \cdot ({\boldsymbol {\sigma }}_{T}\nabla u_{T})=0\quad \quad {\text{in }}\Omega _{T},}$$ ${\displaystyle {\boldsymbol {\sigma }}_{T}}$ ${\displaystyle \Omega _{T}}$

導出

双領域モデルに関しては、いくつかの仮定を置いた上で、マクスウェル方程式と連続方程式から胴体モデルを導くことができる。まず、体内の電気・磁気活動は低レベルで発生するため、準静的仮定を用いることができる。したがって、人体は受動導体とみなすことができ、容量性、誘導性、伝搬性といった効果は無視できる。^{[ 1 ]}

準静的仮定の下では、マクスウェル方程式は^{[ 1 ]} であり 、連続方程式は^{[ 1 ]である。}$${\displaystyle {\begin{cases}\nabla \cdot \mathbf {E} &={\frac {\rho }{\epsilon _{0}}}\\\nabla \times \mathbf {E} &=0\\\nabla \cdot \mathbf {B} &=0\\\nabla \times \mathbf {B} &=\mu _{0}\mathbf {J} \end{cases}}}$$ $${\displaystyle \nabla \cdot \mathbf {J} =0.}$$

回転角がゼロなので、電界はスカラー電位場の勾配、すなわち胴体電位 によって表すことができる。

${\displaystyle \mathbf {E} =-\nabla u_{T}}$

1

ここで負の符号は、電流が電位の高い領域から低い領域へ流れることを意味します。^{[ 1 ]}

そして、全電流密度は伝導電流と他の異なる印加電流によって表すことができ、連続方程式から^{[ 1 ]}

${\displaystyle \nabla \cdot \mathbf {J} =\nabla \cdot (\mathbf {J} _{\text{app}}+{\boldsymbol {\sigma }}_{T}\mathbf {E} )=0}$

2

次に、（１）を（２） に代入すると、$${\displaystyle \nabla \cdot ({\boldsymbol {\sigma }}_{T}\nabla u_{T})=\nabla \cdot \mathbf {J} _{\text{app}}=I_{v}}$$

ここで、単位体積あたりの電流である。^{[ 1 ]}${\displaystyle I_{v}}$

最後に、心臓以外には胴体内に電流源がないので、単位体積あたりの電流はゼロに設定することができ、胴体内の拡散問題の標準的な定式化を表す一般化ラプラス方程式を与える^{[ 1 ]。}$${\displaystyle \nabla \cdot ({\boldsymbol {\sigma }}_{T}\nabla u_{T})=0\quad \quad {\text{in }}\Omega _{T}.}$$

境界条件

境界条件は、胴体を取り囲む媒体、すなわち体周囲の空気の特性を考慮します。一般的に、空気は導電率がゼロであるため、電流は胴体の外側に流れません。これは次の式で表されます^{[ 1 ]。}$${\displaystyle {\boldsymbol {\sigma }}_{T}\nabla u_{T}\cdot \mathbf {n} _{T}=0\quad \quad {\text{on }}\Gamma _{T}}$$

ここで、は胴体に対する単位外向きの法線であり、は胴体境界、つまり胴体表面である。^{[ 1 ] [ 2 ]}${\displaystyle \mathbf {n} _{T}}$ ${\displaystyle \Gamma _{T}}$

胴体の伝導率

通常、胴体は等方性導電率を持つと考えられており、これは電流があらゆる方向に同じように流れることを意味します。しかし、胴体は空虚な均質な包体ではなく、異なる導電率を持つ様々な器官を含んでおり、これらは実験的に得ることができます。骨と肺を考慮した胴体の導電率パラメータの簡単な例を次の表に示します。^{[ 2 ]}

胴体の導電率の値。^{[ 2 ]}

${\displaystyle \sigma _{T}^{\text{lungs}}}$	${\displaystyle \sigma _{T}^{\text{bones}}}$	${\displaystyle \sigma _{T}^{\text{remaining regions}}}$
（秒/センチメートル）	（秒/センチメートル）	（秒/センチメートル）
${\displaystyle 2.4\times 10^{-4}}$	${\displaystyle 4\times 10^{-5}}$	${\displaystyle 6\times 10^{-4}}$

心臓胴体モデル

電気活動モデルと体幹モデル間の結合は、心外膜、すなわち心臓と体幹の界面における適切な境界条件によって実現される。^{[ 1 ] [ 2 ]}

心臓-胴体モデルは、2つの領域間の完全な電気伝達が考慮される場合は完全に結合することができ、心臓の電気モデルと胴体モデルがそれらの間の限定されたまたは不完全な情報交換で別々に解かれる場合は結合を解除することができます。^{[ 2 ]}

心臓と胴体の完全結合モデル

心臓と体幹の完全な結合は、心臓と体幹の間に完全な電気伝達条件を課すことによって達成される。これは、細胞外電位と体幹電位の関係を確立する以下の2つの式を考慮することで実現される^{[ 2 ]。} これらの式は、心外膜を横切る電位と電流の両方の連続性を保証する^{[ 2 ] 。}$${\displaystyle {\begin{aligned}u_{e}&=u_{T}&{\text{on }}\Sigma \\({\boldsymbol {\sigma }}_{e}\nabla u_{e})\cdot \mathbf {n} _{e}&=-({\boldsymbol {\sigma }}_{T}\nabla u_{T})\cdot \mathbf {n} _{T}\quad &{\text{on }}\Sigma .\end{aligned}}}$$

これらの境界条件を用いることで、心臓の電気活動についてバイドメインモデルとモノドメインモデルのいずれかを考慮した、2つの異なる完全結合心臓-体幹モデルを得ることができる。数値的な観点から見ると、2つのモデルは計算コストが非常に高く、計算コストは​​同程度である。^{[ 2 ]}

代替境界条件

心臓と体幹の間の完全な電気的結合を表す境界条件は、最もよく用いられ、古典的なものである。しかし、心臓と体幹の間には心膜が存在する。心膜は二重壁の袋状の組織であり、その中には漿液が含まれており、これが電気伝導に特有の影響を及ぼす。心膜の静電容量 と抵抗効果を考慮すると、この効果を考慮した代替境界条件は以下のように定式化できる^{[ 10 ]。}${\displaystyle C_{p}}$ ${\displaystyle R_{p}}$ $${\displaystyle {\begin{aligned}R_{p}{\boldsymbol {\sigma }}_{e}\nabla u_{e}\cdot \mathbf {n} &=R_{p}C_{p}{\frac {\partial (u_{T}-u_{e})}{\partial t}}+(u_{T}-u_{e})\quad \quad &{\text{on }}\Sigma \\{\boldsymbol {\sigma }}_{e}\nabla u_{e}\cdot \mathbf {n} &={\boldsymbol {\sigma }}_{T}\nabla u_{T}\cdot \mathbf {n} \quad \quad &{\text{on }}\Sigma \end{aligned}}}$$

二領域モデルによる定式化

心臓の電気活動の2領域モデルを考慮した、完全に結合した心臓-胴体モデルの完全な形は^{[ 2 ]} であり 、最初の4つの方程式は2領域モデル、イオンモデル、胴体モデルを表す偏微分方程式であり、残りの方程式は2領域モデルと胴体モデルの境界条件とそれらの間の結合条件を表しています。^{[ 2 ]}$${\displaystyle {\begin{cases}\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla u_{e})=A_{m}\left(C_{m}{\dfrac {\partial V_{m}}{\partial t}}+I_{\text{ion}}(V_{m},w)\right)+I_{\text{app}}&{\text{in }}\Omega _{H}\\[1ex]\nabla \cdot \left(({\boldsymbol {\sigma }}_{i}+{\boldsymbol {\sigma }}_{e})\nabla u_{e}\right)+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})=0&{\text{in }}\Omega _{H}\\[1ex]{\dfrac {\partial w}{\partial {t}}}+g(V_{m},w)=0&{\text{in }}\Omega _{H}\\[1ex]\nabla \cdot ({\boldsymbol {\sigma }}_{T}\nabla u_{T})=0&{\text{in }}\Omega _{T}\\[1ex]({\boldsymbol {\sigma }}_{i}\nabla V_{m})\cdot \mathbf {n} +({\boldsymbol {\sigma }}_{i}\nabla u_{e})\cdot \mathbf {n} =0&{\text{on }}\Sigma \\[1ex]u_{e}=u_{T}&{\text{on }}\Sigma \\[1ex]({\boldsymbol {\sigma }}_{e}\nabla u_{e})\cdot \mathbf {n} =({\boldsymbol {\sigma }}_{T}\nabla u_{T})\cdot \mathbf {n} &{\text{on }}\Sigma \\[1ex]({\boldsymbol {\sigma }}_{T}\nabla u_{T})\cdot \mathbf {n} =0&{\text{on }}\Gamma _{T}\end{cases}}}$$

モノドメインモデルによる定式化

心臓の電気活動に関するモノドメインモデルを考慮した、心臓-体幹完全結合モデルは、バイドメイン問題よりも複雑である。実際、結合条件は体幹電位と細胞外電位を関連付けるが、これはモノドメインモデルでは計算されない。したがって、バイドメインモデルの2番目の式も（モノドメインモデルが導出されたのと同じ仮定の下で）用いる必要があり、以下の式が得られる：^{[ 2 ]}$${\displaystyle \nabla \cdot \left(({\boldsymbol {\sigma }}_{i}+{\boldsymbol {\sigma }}_{e})\nabla u_{e}\right)+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})=0\quad \quad {\text{in }}\Omega _{H}.}$$

この方法では、結合条件を変更する必要がなく、完全な心臓胴体モデルは2つの異なるブロックで構成されます。^{[ 2 ]}

• まず、通常の境界条件を持つモノドメインモデルを解く必要があります。$${\displaystyle {\begin{cases}\chi C_{m}{\dfrac {\partial V_{m}}{\partial t}}-\nabla \cdot \left({\boldsymbol {\sigma }}_{i}{\dfrac {\lambda }{1+\lambda }}\nabla V_{m}\right)+\chi I_{\text{ion}}=I_{\text{app}}&{\text{in }}\Omega _{H}\\[1ex]\left({\boldsymbol {\sigma }}_{i}\nabla V_{m}\right)\cdot \mathbf {n} =0&{\text{on }}\partial \Omega _{H}.\end{cases}}}$$
• 次に、細胞外電位、胴体モデル、結合条件の計算を含む結合モデルを解く必要があります。$${\displaystyle {\begin{cases}\nabla \cdot \left(({\boldsymbol {\sigma }}_{i}+{\boldsymbol {\sigma }}_{e})\nabla u_{e}\right)+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})=0&{\text{in }}\Omega _{H}\\\nabla \cdot ({\boldsymbol {\sigma }}_{T}\nabla u_{T})=0&{\text{in }}\Omega _{T}\\{\boldsymbol {\sigma }}_{T}\nabla u_{T}\cdot \mathbf {n} =0&{\text{on }}\Gamma _{T}\\u_{e}=u_{T}&{\text{on }}\Sigma \\({\boldsymbol {\sigma }}_{e}\nabla u_{e})\cdot \mathbf {n} =({\boldsymbol {\sigma }}_{T}\nabla u_{T})\cdot \mathbf {n} &{\text{on }}\Sigma \end{cases}}}$$

心臓と胴体の分離モデル

心臓と胴体の完全結合モデルは非常に詳細なモデルであるが、解くには計算コストもかかる。^{[ 2 ]}心臓が心臓から完全に電気的に分離されているとみなす、いわゆる非結合仮定によって単純化が可能になる。 ^{[ 2 ]}数学的には、電流が心外膜を通って心臓から胴体へ流れることができないと仮定することで、この仮定が成立する。つまり、^{[ 2 ]}$${\displaystyle {\boldsymbol {\sigma }}_{e}\nabla u_{e}\cdot \mathbf {n} =0\quad \quad {\text{on }}\Sigma .}$$

この方程式を完全結合モデルの境界条件に適用すると、2つの非結合心臓-胴体モデルを得ることができ、電気モデルを胴体モデルとは別に解くことで計算コストを削減することができる。^{[ 2 ]}

二領域モデルによる心臓-胴体分離モデル

心臓の電気活動を表現するためにバイドメインを使用する、完全に結合した心臓-胴体モデルの非結合バージョンは、2つの別々の部分で構成されています。^{[ 2 ]}

• 分離された形態のバイドメインモデル$${\displaystyle {\begin{cases}\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla u_{e})=A_{m}\left(C_{m}{\dfrac {\partial V_{m}}{\partial t}}+I_{\text{ion}}(V_{m},w)\right)+I_{\text{app}}&{\text{in }}\Omega _{H}\\\nabla \cdot \left(({\boldsymbol {\sigma }}_{i}+{\boldsymbol {\sigma }}_{e})\nabla u_{e}\right)+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})=0&{\text{in }}\Omega _{H}\\{\dfrac {\partial w}{\partial {t}}}+g(V_{m},w)=0&{\text{in }}\Omega _{H}\\({\boldsymbol {\sigma }}_{i}\nabla V_{m})\cdot \mathbf {n} +({\boldsymbol {\sigma }}_{i}\nabla u_{e})\cdot \mathbf {n} =0&{\text{on }}\Sigma \\{\boldsymbol {\sigma }}_{e}\nabla u_{e}\cdot \mathbf {n} =0&{\text{on }}\Sigma .\end{cases}}}$$
• 標準的な定式化における胴体拡散モデル、ポテンシャル連続条件付き$${\displaystyle {\begin{cases}\nabla \cdot ({\boldsymbol {\sigma }}_{T}\nabla u_{T})=0&{\text{in }}\Omega _{T}\\{\boldsymbol {\sigma }}_{T}\nabla u_{T}\cdot \mathbf {n} =0&{\text{on }}\Gamma _{T}\\u_{T}=u_{e}&{\text{on }}\Sigma \\\end{cases}}}$$

モドメインモデルを用いた心臓-胴体分離モデル

モノドメインモデルを用いた心臓-胴体完全結合モデルの場合と同様に、対応する非結合モデルにおいても細胞外電位を計算する必要がある。この場合、3つの異なる独立した問題を解く必要がある。^{[ 2 ]}

• 通常の境界条件を持つモノドメインモデル:$${\displaystyle {\begin{cases}\chi C_{m}{\dfrac {\partial V_{m}}{\partial t}}-\nabla \cdot \left({\boldsymbol {\sigma }}_{i}{\dfrac {\lambda }{1+\lambda }}\nabla V_{m}\right)+\chi I_{\text{ion}}=I_{\text{app}}&{\text{in }}\Omega _{H}\\[1ex]\left({\boldsymbol {\sigma }}_{i}\nabla V_{m}\right)\cdot \mathbf {n} =0&{\text{on }}\partial \Omega _{H}.\end{cases}}}$$
• 細胞内電流の流れを規定しない心外膜上の境界条件で細胞外電位を計算する問題：$${\displaystyle {\begin{cases}\nabla \cdot \left(({\boldsymbol {\sigma }}_{i}+{\boldsymbol {\sigma }}_{e})\nabla u_{e}\right)+\nabla \cdot ({\boldsymbol {\sigma }}_{i}\nabla V_{m})=0&{\text{in }}\Omega _{H}\\[1ex]({\boldsymbol {\sigma }}_{i}+{\boldsymbol {\sigma }}_{e})\nabla u_{e}\cdot \mathbf {n} =-({\boldsymbol {\sigma }}_{i}\nabla V_{m})\cdot \mathbf {n} &{\text{on }}\Sigma \end{cases}}}$$
• 心外膜におけるポテンシャル連続境界条件を備えた胴体拡散モデル：$${\displaystyle {\begin{cases}\nabla \cdot ({\boldsymbol {\sigma }}_{T}\nabla u_{T})=0&{\text{in }}\Omega _{T}\\{\boldsymbol {\sigma }}_{T}\nabla u_{T}\cdot \mathbf {n} =0&{\text{on }}\Gamma _{T}\\u_{T}=u_{e}&{\text{on }}\Sigma \\\end{cases}}}$$

心電図計算

心電図における胸部誘導

心臓-体幹完全結合モデルまたは非結合モデルを解くことで、人体体幹のあらゆる点、特に体幹表面全体において心臓が生成する電位を求めることができます。体幹上の電極位置を定義することで、それらの点における電位の時間変化を求めることができます。そして、例えば12の標準誘導に基づいて、以下の式^{[ 2 ]}を用いて心電図を計算することができます。 ここで、およびは電極の標準位置です。^{[ 2 ]}$${\displaystyle {\begin{cases}\mathrm {I} &=u_{T}(L)-u_{T}(R)\\\mathrm {II} &=u_{T}(F)-u_{T}(R)\\\mathrm {III} &=u_{T}(F)-u_{T}(L)\\\mathrm {aVR} &={\frac {3}{2}}(u_{T}(R)-u_{w})\\\mathrm {aVL} &={\frac {3}{2}}(u_{T}(L)-u_{w})\\\mathrm {aVF} &={\frac {3}{2}}(u_{T}(F)-u_{w})\\\mathrm {V} _{i}&=u_{T}(V_{i})-u_{w}\quad i=1,\dots ,6\end{cases}}}$$ ${\displaystyle u_{W}=(u_{T}(L)+u_{T}(R)+u_{T}(F))/3}$ ${\displaystyle L,R,F,\{V_{i}\}_{i=1}^{6}}$

数値解析法

心臓-胴体モデルは、未知数が空間と時間の両方の関数である偏微分方程式で表現されます。これらは、通常、常微分方程式系で表されるイオンモデルと結合されます。これらの問題の解法には、様々な数値計算法が用いられます。通常、空間離散化には有限要素法が、時間離散化には半暗黙差分法が用いられます。^{[ 1 ] [ 2 ]}

心臓-体幹非結合モデルは、心臓の電気モデルを体幹モデルとは独立して解くことができるため、数値解析的に扱うのが最も容易です。そのため、それぞれに古典的な数値解析手法を適用できます。つまり、バイドメインモデルとモノドメインモデルは、例えば時間離散化のための後退微分公式を用いて解くことができます。一方、細胞外電位と体幹電位を計算する問題は、時間に依存しないため、有限要素法のみを適用することで容易に解くことができます。^{[ 1 ] [ 2 ]}

一方、心臓-胴体完全結合モデルはより複雑であり、より洗練された数値モデルが必要となる。例えば、心臓挙動の電気的シミュレーションにバイドメインモデルを用いる心臓-胴体完全結合モデルは、ディリクレ-ノイマン領域分割法などの領域分割手法を用いて解くことができる。 ^{[ 2 ] [ 11 ]}

幾何学的な胴体モデル

最も多くの臓器を含む3次元胴体モデル。^{[ 12 ]}

完全結合モデルまたは非結合モデルを用いて心電図をシミュレーションするには、人体胴体の3次元再構成が必要です。今日では、MRIやCTなどの診断画像技術は、人体の解剖学的部位を詳細に再構成し、適切な胴体形状を得るのに十分な精度の画像を提供できます。例えば、Visible Human Data ^{[ 13 ]}は、骨格構造や筋肉を含む内臓まで詳細に再現された3次元胴体モデルを作成するための有用なデータセットです。^{[ 1 ]}

心電図の動的モデル

たとえ結果が非常に詳細であったとしても、3次元モデルを解くのは通常非常にコストがかかります。簡略化の方法として、3つの常微分方程式を結合した力学モデルがあります。^{[ 3 ]}

心拍の準周期性は、平面上の吸引リミットサイクルを囲む3次元軌道によって再現される。心電図の主要なピークであるP波、Q波、R波、S波、T波は、固定角度で表され、以下の3つの常微分方程式を与える^{[ 3 ] 。}${\displaystyle (x,y)}$ ${\displaystyle \theta _{P},\theta _{Q},\theta _{R},\theta _{S}{\text{ and }}\theta _{T}}$

$${\displaystyle {\begin{aligned}x'&=\alpha z-\omega y\\[1ex]y'&=\alpha y+\omega x\\[1ex]z'&=\textstyle -\sum _{i\in \{P,Q,R,S,T\}}a_{i}\Delta \theta _{i}{\text{exp}}\left(-{\Delta \theta _{i}^{2}}/{2b_{i}^{2}}\right)-(z-z_{0})\end{aligned}}}$$ と、、${\textstyle \alpha =1-{\sqrt {x^{2}+y^{2}}}}$ ${\displaystyle \Delta \theta _{i}=(\theta -\theta _{i}){\bmod {(}}2\pi )}$ ${\displaystyle \theta ={\text{atan}}2(y,x)}$

これらの方程式は、常微分方程式のルンゲ・クッタ法のような古典的な数値アルゴリズムで簡単に解くことができます。^{[ 3 ]}

参照

• モノドメインモデル
• バイドメインモデル
• 心電図検査

参考文献

1. , Andrew J.; Buist, Martin L.; Cheng, Leo K. (2005).心臓の電気的活動の数学的モデル化：細胞から体表面へ、そして再び細胞へ. World Scientific. ISBN 978-981-256-373-6。
2. 、ムリエル;カゾー、セルジュ。フェルナンデス、ミゲル A.ジェルボー、ジャン・フレデリック。ゼムゼミ、ネジブ（2009年12月24日）。「心電図の数学的モデリング: 数値研究」(PDF)。生体医工学年報。38 (3): 1071–1097。土井: 10.1007/s10439-009-9873-0。PMID 20033779。S2CID 10114284。  
3. McSharry, PE; Clifford, GD; Tarassenko, L.; Smith, LA (2003年3月). 「合成心電図信号を生成するための動的モデル」. IEEE Transactions on Biomedical Engineering . 50 (3): 289– 294. CiteSeerX 10.1.1.65.2929 . doi : 10.1109/TBME.2003.808805 . PMID 12669985. S2CID 544816 .   
4. Lines, GT; Buist, ML; Grottum, P.; Pullan, AJ; Sundnes, J.; Tveito, A. (2002年7月1日). 「心臓電気生理学における順問題のための数学モデルと数値解析法」. Computing and Visualization in Science . 5 (4): 215– 239. doi : 10.1007/s00791-003-0101-4 . S2CID 123211416 . 
5. アイントホーフェン、ウォーラー (1903)。「生理機能における心電図記録、心電図検査、毛細血管電気計の検査」。プフルーガーズ アーカイブ。99 ( 9–10 ): 472–480 .土井: 10.1007/BF01811855。S2CID 10400303。 
6. Henriquez, CS; Plonsey, R. (1987). 「単一心筋線維における抵抗性不連続性による波形と速度への影響」Med . Biol. Eng. Comput . 25 (4): 428– 438. doi : 10.1007/BF02443364 . PMID 3450994. S2CID 3038844 .  
7. Muller-Borer, BJ; Erdman, DJ; Buchanan, JW (1994). 「解剖学的にモデル化された心室組織における電気的結合とインパルス伝播」. IEEE Trans. Biomed. Eng . 41 (5): 445– 454. doi : 10.1109/10.293219 . PMID 8070804. S2CID 14407776 .  
8. Hren, R.; Nenonen, J.; Horacek, BM (1998). 「ペースメーカ活性化時の心外膜電位マップのシミュレーションは心筋線維構造を反映する」Annals of Biomedical Engineering . 26 (6): 1022– 1035. doi : 10.1114/1.73 . PMID 9846940. S2CID 9978399 .  
9. キーナー、ジェームズ; スネイド、ジェームズ (2009).数理生理学 2009: システム生理学 II (第2改訂版). シュプリンガー. ISBN 978-1-4939-3709-7。
10. Boulakia, Muriel; Fernández, Miguel A.; Gerbeau, Jean-Frédéric; Zemzemi, Nejib (2007). 「心電図の数値シミュレーションに向けて」.心臓の機能イメージングとモデリング. コンピュータサイエンス講義ノート. Vol. 4466. Springer. pp.  240– 249. doi : 10.1007/978-3-540-72907-5_25 . ISBN 978-3-540-72906-8。
11. Fernández, Miguel A.; Zemzemi, Nejib (2010年7月1日). 「計算心臓電気生理学およびECG数値シミュレーションにおける分離型時間進行スキーム」(PDF) . Mathematical Biosciences . 226 (1 ) : 58– 75. doi : 10.1016/j.mbs.2010.04.003 . ISSN 0025-5564 . PMID 20416327. S2CID 8792966 .   
12. アナ・フェレール;セバスチャン、ラファエル。サンチェス・キンタナ、ダミアン。ロドリゲス、ホセ F.ゴドイ、エドゥアルド J.マルティネス、ローラ。サイズ、ハビエル（2015年11月2日）。「心房活性化のシミュレーションのための人間の心房と胴体の詳細な解剖学的および電気生理学的モデル」。プロスワン。10 (11) e0141573。ビブコード: 2015PLoSO..1041573F。土井：10.1371/journal.pone.0141573。ISSN 1932-6203。PMC 4629897。PMID 26523732。   
13. Spitzer, V.; Ackerman, MJ; Scherzinger, AL; Whitlock, D. (1996年3月1日). 「目に見える人間の男性：技術報告」 .米国医療情報学会誌. 3 (2): 118– 130. doi : 10.1136/jamia.1996.96236280 . PMC 116294. PMID 8653448 .