Kobon三角形の問題

3本、4本、5本の直線で生成されるKobon三角形

数学における未解決問題

線を並べると、重なり合わない三角形がいくつ形成されますか?${\displaystyle k}$

数学におけるさらなる未解決問題

コーボン三角形問題は、藤村コーボン（1903-1983）によって初めて提唱された組合せ幾何学における未解決問題である。この問題は、 k本の直線の配列上に辺が重ならない三角形の個数N ( k )の最大値を求めるものである。この問題の変種では、ユークリッド平面ではなく射影平面が考慮され、三角形が配列の他のどの直線とも交差しないことが求められる。^{[ 1 ]}

既知の上限

田村三郎は、直線で実現できる重なり合わない三角形の数は最大で であることを証明しました。G. ClémentとJ. Baderは、が6を法として0または2と合同な場合、この上限は達成できないことをより強く証明しました。 ^{[ 2 ]}したがって、これらの場合、三角形の最大数は最大で1つ少なくなります。同じ上限は、床関数を使用せずに、次のように 同等に述べることができます${\displaystyle k}$ ${\displaystyle \lfloor k(k-2)/3\rfloor }$ ${\displaystyle k}$ $${\displaystyle {\begin{cases}{\frac {1}{3}}k(k-2)&{\text{k\equiv 3.5{\pmod {6}}の場合;\\{\frac {1}{3}}(k+1)(k-3)&{\text{k\equiv 0.2{\pmod {6}}の場合;\\{\frac {1}{3}}(k^{2}-2k-2)&{\text{k\equiv 1.4{\pmod {6}}の場合.\end{cases}}}$$

が3、4、5、6、7、8、9、13、15、17、19、21、23、25、27、29、31、または33の場合、この数の三角形を生み出す解が知られています。^{[ 3 ] [ 4 ] [ 5 ]} k = 10、11、12 の場合、既知の最良の解は、この上限より1つ少ない三角形の数に達します。 ${\displaystyle k}$

さらに、偶数値の上限も改善できる。^{[ 4 ]}この上限は10、12、16で達成できる。^{[ 3 ]}${\displaystyle k}$ ${\displaystyle \lfloor k(k-7/3)/3\rfloor }$

k = 11の上限は長い間到達不可能であると考えられていましたが、2025年にパブロ・サフチュクがSATソルバーを用いて正しいことが示されました。^{[ 6 ]}

既知の構成

以下の境界が知られています。

k	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21		23		25		27		29		31		33	OEIS
N ( k )に関する田村の上限	1	2	5	8	11	16	21	26	33	40	47	56	65	74	85	96	107	120	133		161		191		225		261		299		341	A032765
田村の改良[ 2 ] [ 4 ] [ 6 ]	1	2	5	7	11	15	21	25	32	38	47	54	65	72	85	94	107	117	133		161		191		225		261		299		341	-
最もよく知られている解決策	1	2	5	7	11	15	21	25	32	38	47	53	65	72	85	93	107	116	133		161		191		225		261		299		341	A006066

射影平面において

五芒星を形成する5本の直線と、その下に1本の水平線を引いた線は、7つの三角形を形成します。そのうち5本は五芒星に、残りの2本は五芒星の角から発する2対の光線によって形成されます。下の水平線を射影平面の無限遠直線まで移動させると、五芒星から発する5対の光線はすべて、それと三角形を形成します。

射影平面における問題のバージョンでは、より多くの三角形が許容されます。このバージョンでは、与えられた直線の1つとして無限遠直線を含めるのが便利です。これにより、三角形は3つの形で現れます。

• 残りの線分の間には、3つの有限線分で囲まれた通常の三角形があり、
• 共通の頂点で交わる2本の直線と無限遠点の線分で囲まれた三角形、および
• 有限の線分と、無限遠直線上の頂点で交わる 2 本の平行光線によって囲まれた三角形。

たとえば、5 本の有限の線で五芒星を形成し、無限遠の 6 番目の線を合わせると、10 個の三角形ができます。五芒星の中に 5 つ、さらに 5 つが光線のペアで囲まれています。

D. ForgeとJL Ramirez Alfonsinは、射影平面における直線と三角形（ の最大値）の配置（ ）から、特定の追加特性を持つ直線と三角形（これも最大値）の別の解（同じ追加特性を持つ）へと移行する方法を提示した。彼らが指摘するように、この方法は、前述の6本の直線と10個の三角形の射影配置から始めることができ、直線の数が ${\displaystyle k>3}$ ${\displaystyle {\tfrac {1}{3}}k(k-1)}$ ${\displaystyle k>3}$ ${\displaystyle K=2k-1}$ ${\displaystyle {\tfrac {1}{3}}K(K-1)}$

6、11、21、41、81、...。

このように、射影的な場合には、最適解が知られている直線の数は無限に存在する。^{[ 1 ]}

擬似直線配置において

ユークリッド平面上の三角形に関する従来の問題は、しばしば2つの部分に分けられます。擬似直線の配置における同値問題と、最適な三角形数を持つ擬似直線配置の伸縮性の問題です。擬似直線を扱う場合、パップスの定理やデザルグの定理のような規則に違反することを心配することなく、純粋な組合せ論と群論を活用できます。^{[ 4 ] [ 7 ]}

擬似直線配置は、直線配置と組み合わせ的に等価である場合に伸縮可能であると言われます。つまり、各直線が交差する順序を維持しながら各直線をまっすぐにすることができますが、実数の存在理論では伸縮可能な配置と伸縮不可能な配置を区別することは完全です。 ^{[ 8 ] [ 9 ]}

例

• 
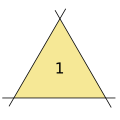
  3本の線、1つの三角形
• 
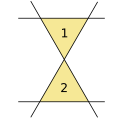
  4本の線、2つの三角形
• 
  5本の線、5つの三角形
• 
  6本の線、7つの三角形
• 
  7本の線、11個の三角形

19本の線、107個の三角形	21本の線、133個の三角形

参照

• ロバーツの三角形定理、直線が形成できる三角形の最小数に関するもの${\displaystyle n}$

参考文献

1. Forge, D.; Ramírez Alfonsín, JL (1998)、「実射影平面における直線配置」、離散および計算幾何学、20 (2): 155– 161、doi : 10.1007/PL00009373。
2. 「G. ClémentとJ. Bader. Kobon三角形の数のより厳しい上限。草稿版、2007年」(PDF) 。 2017年11月11日にオリジナル(PDF)からアーカイブ。2008年3月3日閲覧
3. エド・ペッグ・ジュニアによる数学ゲーム
4. Bartholdi, Nicolas; Blanc, Jérémy; Loisel, Sébastien (2008) 「三角形の最大数を含む、および三角形の最大数を含む線と擬似線の単純な配置について」 (PDF)、Goodman, Jacob E.、Pach, János、Pollack, Richard (編)、「離散幾何学および計算幾何学に関する調査: ユタ州スノーバードで 2006 年 6 月 18 ～ 22 日に開催された第 3 回 AMS–IMS–SIAM 合同夏季研究会議「離散幾何学および計算幾何学 - 20 年後」の議事録、Contemporary Mathematics、vol. 453、プロビデンス、ロードアイランド：アメリカ数学会、pp.  105– 116、arXiv：0706.0723、doi：10.1090/conm/453/08797、ISBN${\displaystyle \mathbb {P} ^{2}}$ ${\displaystyle \mathbb {R}^{2}}$  978-0-8218-4239-3、MR  2405679
5. A006066
6. Savchuk, Pavlo (2025). 「テーブルエンコーディング、SATソルビング、ヒューリスティックストレートニングによる最適なKobon三角形配置の構築」arXiv : 2507.07951 [ math.CO ].
7. フェルスナー, ステファン; グッドマン, ジェイコブ E. (2017). 「擬似線配置」(PDF) .離散幾何学および計算幾何学ハンドブック(第3版). チャップマン・アンド・ホール/CRC. ISBN 9781315119601。
8. Shor, PW (1991)、「擬似直線の伸縮性はNP困難である」、Gritzmann, P.、Sturmfels, B. (編)、『応用幾何学と離散数学：Victor Klee記念論文集』、DIMACSシリーズ、離散数学と理論計算機科学、第4巻、プロビデンス、ロードアイランド州：アメリカ数学会、pp.  531– 554
9. Schaefer, Marcus (2010)、「いくつかの幾何学的および位相的問題の複雑性」(PDF)、グラフ描画、第17回国際シンポジウム、GS 2009、シカゴ、イリノイ州、米国、2009年9月、改訂論文、Lecture Notes in Computer Science、vol. 5849、Springer-Verlag、pp.  334– 344、doi : 10.1007/978-3-642-11805-0_32、ISBN 978-3-642-11804-3、2021年6月26日にオリジナルからアーカイブ（PDF） 、 2024年10月16日閲覧

外部リンク

• ヨハネス・バーダー、「コボンの三角形」