帰納的推論

帰納的推論とは、議論の結論が演繹的な確実性ではなく、せいぜいある程度の確率で裏付けられる様々な推論方法を指します。前提が正しいとすれば結論が確実となる演繹的推論（数学的帰納法など）とは異なり、帰納的推論は、提示された証拠を前提とすれば、せいぜい蓋然性の高い結論を導き出します。[ 1 ]

種類

帰納的推論の種類には、一般化、予測、統計的三段論法、類推、因果推論などがあります。また、結果の捉え方にも違いがあります

帰納的一般化

一般化（より正確には、帰納的一般化）は、標本に関する前提から母集団に関する結論へと進みます。[ 2 ]この標本から得られた観察結果は、より広い母集団に投影されます。[ 2 ]

サンプルの割合 Q には属性 A があります。
したがって、人口の割合 Q は属性 A を持ちます。

たとえば、壺の中に黒または白のボールが 20 個入っているとします。それぞれのボールの個数を推定するために、サンプルとして4 個のボールが取り出され、そのうち 3 個は黒、1 個は白です。帰納的に一般化すると、壺の中には 15 個の黒ボールと 5 個の白ボールがあるということになります。しかし、これは壺 (母集団)の中の各色のボールの実際の個数に関する 17 通りの可能性のうちの 1 つに過ぎません。もちろん、黒ボールが 19 個で白ボールが 1 個だけだった可能性もあれば、黒ボールが 3 個で白ボールが 17 個だった可能性もあれば、その中間の混合だった可能性もあります。それぞれの分布が黒ボールと白ボールの実際の個数である確率は、ベイズ推論(分布についての事前仮定を観測サンプルで更新する) や最尤推定(MLE) (観測サンプルを与えられた場合に最も可能性の高い分布を識別する) などの手法を使用して推定できます。

前提が結論をどの程度裏付けるかは、標本集団の人数、母集団の人数、そして標本が母集団をどの程度代表しているか（静的な母集団であれば、無作為標本を採取することで実現できる）によって決まる。標本が母集団をどの程度代表しているかは、個々の観察に用いられる手順の信頼性によって決まるが、これは必ずしも静的な母集団から無作為な要素を採取するほど単純ではなく、それ自体も必ずしも単純ではない。母集団に対する標本サイズが大きいほど、また標本が母集団をよりよく代表するほど、一般化は強くなる。性急な一般化と偏った標本は、一般化の誤謬である。

統計的一般化

統計的一般化とは、統計的に代表的な標本を用いて母集団に関する結論を推論する帰納的議論の一種です。例：

調査対象となったかなりの数の有権者の無作為抽出サンプルのうち、66%が法案Zを支持し​​ている。
したがって、有権者の約 66% が法案 Z を支持しています。

この指標は、選択プロセスが真にランダムであり、サンプル内で考慮されている特性を持つ項目の数が多い場合、明確に定義された誤差範囲内で高い信頼性があります。これは容易に定量化できます。前の議論と次の議論を比較してください。「私の読書クラブのメンバー10人のうち6人はリバタリアンです。したがって、約60%の人がリバタリアンです。」この議論は、サンプルがランダムではなく、サンプルサイズが非常に小さいため、説得力がありません。

統計的一般化は統計的予測[ 3 ]や標本予測[ 4 ]とも呼ばれる。

逸話的一般化

逸話的一般化とは、統計的ではないサンプルを用いて母集団に関する結論を推論する帰納的議論の一種です。[ 5 ]言い換えれば、一般化は逸話的証拠に基づいています。例えば：

今のところ、今年、彼の息子のリトルリーグチームは10試合中6試合勝っている。
したがって、シーズンの終わりまでに、彼らは約 60% の試合に勝つことになります。

この推論は統計的な一般化よりも信頼性が低く（したがって、性急な一般化の誤謬に陥る可能性が高い）、第一に、サンプルとなる事象がランダムではないこと、第二に、数式に還元できないことがその理由である。統計的に言えば、将来起こるであろうパフォーマンスに影響を与える状況を知り、測定し、計算する方法は存在しない。哲学的なレベルでは、この議論は、将来の事象の作用が過去を反映するという前提に依存している。言い換えれば、自然の均一性、つまり経験的データ自体からは導き出せない未証明の原理を当然のこととしている。この均一性を暗黙のうちに前提とする議論は、それらを哲学的精査に初めてかけた哲学者にちなんで、ヒューム的と呼ばれることがある。 [ 6 ]

予測

帰納的予測は、他の事例のサンプルから、将来、現在、または過去の事例についての結論を導き出します。帰納的一般化と同様に、帰納的予測は、現象の特定の事例からなるデータセットに依存します。しかし、帰納的予測は、一般的な記述で結論付けるのではなく、単一の事例が他の事例と共有する（または共有しない）属性を持つ（または持たない）確率に関する具体的な記述で結論付けます。[ 7 ]

グループ G の観察対象メンバーのうち、属性 A を持つメンバーの割合 Q です。
したがって、次に観察されたときにグループ G の他のメンバーが属性 A を持つ確率は Q に相当します。

統計的三段論法

統計的三段論法は、集団についての一般化から個人についての結論へと進みます

集団 P の既知のインスタンスの割合 Q には属性 A があります。
個人IはPの別のメンバーです。
したがって、Qに対応する確率で、IはAを持っていることになります。

例えば：

エクセルシオール予備校の卒業生の90%は大学に進学します
ボブはエクセルシオール予備校の卒業生です。
したがって、ボブはおそらく大学に進学するでしょう。

これは統計的三段論法である。[ 8 ]ボブが大学に進学するかどうかは確実ではないものの、（それ以上の情報がなければ）この結果の正確な確率は完全に保証されている。統計的三段論法には、「偶然」と「逆偶然」という2つの「ディクト・シンプリシターの誤謬」が起こり得る。

類推による議論

類推推論のプロセスは、2つ以上のものの共通の性質に注目し、それに基づいてそれらがさらに何らかの性質を共有していると推論することを含みます。[ 9 ]

P と Q は、特性 a、b、c に関して類似しています。
オブジェクト P にはさらなる特性 x があることが観察されています。
したがって、Q にはおそらくプロパティ x もあります。

類推的推論は常識、科学、哲学、法律、人文科学の分野で非常に頻繁に用いられますが、補助的な方法としてのみ受け入れられる場合もあります。より洗練されたアプローチは事例に基づく推論です。[ 10 ]

鉱物 A と鉱物 B はどちらも火成岩であり、多くの場合石英の脈を含んでおり、南アメリカの古代の火山活動の地域でよく見られます。
鉱物Aも、ジュエリーに彫刻するのに適した柔らかい石です。
したがって、鉱物 B はおそらく、宝飾品に彫刻するのに適した柔らかい石であると考えられます。

これは類推帰納法であり、ある点において類似しているものは、他の点においても類似している可能性が高いとされています。この帰納法は、哲学者ジョン・スチュアート・ミルが著書『論理体系』の中で詳細に考察しており、「（無関係であると知られていない）あらゆる類似性は、そうでなければ存在するであろう以上の、結論を支持するある程度の確率を与えることは疑いの余地がない」と述べています。[ 11 ]ミルの方法を参照。

一部の思想家は、類推帰納法は事象を支配する一定の均一性を前提とするため、帰納的一般化のサブカテゴリーであると主張しています。類推帰納法では、2つの石に共通するとされる特徴の関連性について、補助的な検討が必要です。前述の例において、両方の石が初期のスペイン人探検家の記録に記載されているという前提が付け加えられたとしても、この共通の属性は石とは無関係であり、それらの類似性の可能性には寄与しません。

類推の落とし穴は、特徴が恣意的に選ばれてしまう可能性があることです。物体は驚くほど類似している一方で、並置された二つのものが、類推では特定されていない、大きく異なる別の特徴をそれぞれ持っている場合があります。したがって、関連する比較をすべて行わなければ、類推は誤った結果をもたらす可能性があります。

因果推論

因果推論とは、結果の発生条件に基づいて、可能性のある、あるいは確からしい因果関係について結論を導き出すことです。2つの事柄の相関関係に関する前提は、それらの間の因果関係を示唆する可能性がありますが、因果関係の正確な形を確立するには、追加の要因を確認する必要があります

方法

帰納的一般化に至るために使用される2つの主要な方法は、列挙帰納法と消去帰納法です。[ 12 ] [ 13 ]

列挙的帰納法

列挙帰納法は、一般化を、それを支持する事例の数に基づいて構築する帰納的方法である。支持する事例の数が多いほど、結論は強くなる。[ 12 ] [ 13 ]

最も基本的な形式の列挙帰納法は、特定の事例からすべての事例を推論するものであり、したがって無制限の一般化である。[ 14 ] 100羽の白鳥を観察し、そのすべてが白い場合、「すべての白鳥は白い」という形式の蓋然的な普遍的定言命題を推論するかもしれない。この推論形式の前提は、たとえ正しくても結論の真理性を含意しないため、これは帰納的推論の一種である。結論は真である可能性があり、おそらく真であると考えられるかもしれないが、偽である可能性もある。列挙帰納法は科学的方法の伝統的なモデルにおいて極めて重要な役割を果たすため、列挙帰納法の正当性と形式に関する問題は科学哲学において中心的な問題となっている。

これまでに発見されたすべての生命体は細胞で構成されています。
したがって、すべての生命体は細胞で構成されています。

これは列挙帰納法であり、単純帰納法または単純予測帰納法とも呼ばれます。これは帰納的一般化のサブカテゴリです。日常の実践では、これはおそらく最も一般的な帰納法の形式です。前の議論では、結論は魅力的ですが、証拠をはるかに超えた予測を行っています。まず、現在までに観察された生命体から将来のケースがどうなるかがわかると仮定しています。これは均一性への訴えです。次に、すべてという結論は大胆な主張です。1つの反対の例が議論をくじきます。そして最後に、確率のレベルを数学的な形式で定量化することは問題があります。[ 15 ]どのような基準で、地球上の既知の生命のサンプルをすべての（可能性のある）生命と比較するのでしょうか。中間圏や小惑星に浮遊する微生物など、細胞を持つ新しい生物を発見したとします。この補強証拠が追加されたことで、主題の命題の確率評価を引き上げる義務が生じるのでしょうか。この質問に「はい」と答えるのが一般的に合理的とみなされており、多くの人にとってこの「はい」は合理的であるだけでなく、反駁の余地もありません。では、この新たなデータは私たちの確率評価をどの程度変えるべきなのでしょうか？ここでコンセンサスは崩れ去り、代わりに、数値化の有無にかかわらず、確率について首尾一貫して議論できるのかという疑問が生じます。

これまで発見されたすべての生命体は細胞で構成されています。
したがって、次に発見される生命体は細胞で構成されるでしょう。

これは弱い形の列挙帰納法である。「すべて」を単なる一つの例に切り捨て、はるかに弱い主張をすることで、結論の確率をかなり高めている。それ以外は、強い形と同じ欠点がある。つまり、標本母集団はランダムではなく、数量化の手法も難しい。

排除的帰納法

排除的帰納法は、変分帰納法とも呼ばれ、フランシス・ベーコンによって初めて提唱された帰納法です。[ 16 ]一般化は、それを支持する事例の多様性に基づいて構築されます。列挙的帰納法とは異なり、排除的帰納法は、結論を支持する事例の数ではなく、結論を支持する様々な種類の事例に基づいて推論します。事例の多様性が増えるにつれて、それらの事例に基づく結論の可能性のうち、矛盾すると特定され排除されるものが増えます。これにより、様々な事例と一致する結論の強度が増します。この文脈において、確信度は、矛盾すると特定され排除された事例の数の関数です。この確信度は、主張が矛盾すると判断するn個の理由が特定され、そのうちi個が証拠または議論によって排除された場合のベーコン確率（「n個中i個」と読みます）として表されます。[ 16 ]

議論を攻撃する方法は3つあります。これらは、反駁、貶め、そして貶め（defeaters）と呼ばれ、反証可能推論の文献では「貶め」として知られています。反駁は反例を提示することで、貶めは証拠の妥当性に疑問を投げかけることで、貶めは貶め、そして貶めは推論が正しいのに結論が間違っている状況を指摘することで、貶めは貶めます。貶めを特定し、それが誤りであることを証明することで、このアプローチは信頼を築きます。[ 16 ]

このタイプの帰納法では、疑似実験などの異なる方法論が用いられることがあり、疑似実験では、対立する仮説を検証し、可能であれば排除する。[ 17 ]また、考えられる可能性を排除するために、異なる証拠テストが用いられることもある。[ 18 ]

排除的帰納法は科学的方法にとって非常に重要であり、観察や実験と矛盾する仮説を排除するために使用されます。[ 12 ] [ 13 ]これは、因果関係の実際の観察例ではなく、考えられる原因に焦点を当てています。[ 19 ]

排除的帰納法は、すべての妥当な競合仮説を特定してからそれらを排除する必要があるという点でも批判されてきた。サルモンは、既存の代替仮説を除外した後でも新たな説明が出現する可能性があるため、この要件は科学の実践ではほとんど達成できないと指摘しており、この方法が提供できる確実性は限られている。[ 20 ]トレッティも同様に、排除的戦略は、複数の異なる仮説が同じ証拠と適合し続ける可能性があるという、より広範な不確定性の問題に直面していると主張している。そのため、可能性の空間が既に明確に定義されていない限り、排除は不完全となる。[ 21 ]

歴史

古代哲学

紀元前300年代、アリストテレスは個別的なものから普遍的なものへの移行として、ギリシャ語の「epagogé（エパゴゲ）」を使用し、キケロはそれをラテン語の「inductio（インダクション）」に翻訳しました。[ 22 ]

アリストテレスと逍遥学派

アリストテレスの『後分析論』は、自然哲学と社会科学における帰納的証明の方法を網羅しています。『後分析論』の第一巻では、証明の性質と科学、そしてその要素について、定義、分類、第一原理の直観的推論、個別的証明と普遍的証明、肯定的証明と否定的証明、科学と意見の違いなどについて解説しています。

ピュロン主義

古代ピュロン主義者は、帰納法の問題を指摘した最初の西洋哲学者でした。彼らによれば、帰納法は普遍的な命題を真実として受け入れることを正当化できないということです。[ 22 ]

古代医学

古代ギリシャ医学の経験主義学派は、推論の方法としてエピローグ主義を採用しました。「エピローグ主義」とは、理論に基づかない方法であり、大げさな一般化をすることなく、因果関係の主張を行うことの結果を考慮しながら、事実の蓄積を通して歴史を考察します。 [ 23 ]エピローグ主義は、目に見える明白な事柄の領域内で完全に行われる推論であり、観察不可能なものを持ち出そうとはしません

古代ギリシャ医学のドグマティック学派は推論の方法としてアナロギズムを採用した。[ 24 ]この方法は、観察されたものから観察できない力までを類推して推論するものである。

近世哲学

1620年、近世哲学者フランシス・ベーコンは、単なる経験と列挙的帰納法のみの価値を否定した。彼の帰納主義の方法論によれば、自然界の構造と因果関係を明らかにする緻密かつ多様な観察は、列挙的帰納法と結びついて初めて、現在の経験の範囲を超えた知識を得ることができるとされた。したがって、帰納主義は列挙的帰納法を構成要素として必要とした。

デイヴィッド・ヒューム

経験主義者デイヴィッド・ヒュームの1740年の立場は、列挙帰納法には論理的根拠どころか、合理的な根拠もないというものでした。帰納法は理性ではなく本能の産物であり、心の習慣であり、日々の生活の要件であると考えました。太陽の運動などの観察は、自然の均一性の原理と組み合わせることで、確実と思われる結論を導き出すことができますが、帰納法の問題は、自然の均一性が論理的に有効な原理ではないという事実から生じました。したがって、演繹的に合理的であると擁護することはできませんでしたが、自然の均一性が過去を正確に記述してきたため、未来も正確に記述する可能性が高いという事実を理由に帰納的に合理的であると擁護することもできませんでした。なぜなら、それは帰納的な議論であり、帰納法こそが正当化されるべきものであるため、循環論法だからです

ヒュームが初めて自然の均一性を支持する演繹的議論の妥当性と帰納的議論の循環性との間のジレンマについて書いて以来、演繹と帰納という単なる2つの推論モード間のこの想定された二分法は、アブダクションまたはアブダクション的推論として知られる第3の推論モードの発見によって異論を唱えられてきた。アブダクションまたはアブダクション的推論は、1886年にチャールズ・サンダース・パースによって初めて定式化され提唱され、彼はそれを「仮説による推論」と呼んだ。[ 25 ] 最善の説明への推論は、1965年にギルバート・ハーマンによって初めて「アブダクション的推論」と認識されたため、しばしば、しかし議論の余地はあるものの、アブダクションと同義として扱われるが、彼のアブダクションの定義は、パースの定義とわずかに異なる。[ 26 ] いずれにせよ、もしアブダクションが他の二つから合理的に独立した第三の推論様式であるならば、自然の均一性はアブダクションによって合理的に正当化されるか、あるいはヒュームのジレンマはよりトリレンマに近いものとなる。ヒュームはまた、観測不可能なものについての確実性に到達するために列挙的帰納法と理性を適用すること、特に関係性のある側面を修正することで特定の結果が防止されるか生じるかという事実から因果関係を推論することに懐疑的であった。

イマヌエル・カント

ヒュームの著作のドイツ語訳によって「独断的な眠り」から覚めたカントは、形而上学の可能性を説明しようとした。1781年、カントの『純粋理性批判』は、経験主義とは異なる知識への道として合理主義を紹介した。カントは言明を2種類に分類した。 分析的言明は、その用語と意味の配置によって真となるため、分析的言明はトートロジー（同義語）にすぎず、必然的に真となる論理的真理にすぎない。一方、総合的言明は、事実の状態、偶然性を指す意味を持つ。カントの『純粋理性批判』は、デカルトやライプニッツのような合理主義哲学者と、ロックやヒュームのような経験主義哲学者の両方に対して、知識を得るためには精神（概念）の寄与と感覚（直観）の寄与の両方が必要であるという主張を貫いている。カントにとって、知識そのものは、私たちが知覚できるもの（現象）に限定されるが、単なる思考の対象（「物自体」）は、知覚することが不可能であるため、原理的に知ることができない。

カントは、感覚データを組織化し、空間と時間（現象）におけるオブジェクトの経験を可能にする独自のカテゴリーが心の中になければならないという推論から、自然の均一性はアプリオリな真理であると結論した。 [ 20 ]偶然ではなく必然的に真で ある総合的な命題のクラスは、アプリオリに総合的であった。カントはこうして形而上学とニュートンの万有引力の法則の両方を救った。我々の認識を超えるものは「我々には何もない」という議論に基づいて、[ 27 ]彼は科学的実在論を放棄した。認識は知覚と思考能力の協力によって生じる（超越論的観念論）というカントの立場は、ドイツ観念論の運動を生み出した。 ヘーゲルの絶対観念論はその後、ヨーロッパ大陸とイギリスで栄えた。

後期近代哲学

実証主義は、アンリ・ド・サン＝シモンによって発展させ、1830年代に彼のかつての教え子であるオーギュスト・コントによって広められ、後期近代科学哲学の最初であった。フランス革命の余波で、社会の破滅を恐れたコントは、形而上学に反対した。コントによれば、人類の知識は宗教から形而上学、そして科学へと進化し、数学から天文学、物理学、化学、生物学、社会学へとこの順序で流れ、ますます複雑な領域を記述してきた。社会の知識はすべて科学的になり、神学や形而上学の問いには答えられなくなった。コントは、利用可能な経験に基づいているため、列挙帰納法は信頼できると考えた。彼は、人類社会を改善するための正しい方法として、形而上学的真理ではなく科学を用いるべきだと主張した。

コントによれば、科学的方法は予測を立て、それを確認し、神学や形而上学によって反駁できない法則（肯定的陳述）を述べる。経験は自然の均一性を実証することによって列挙帰納法を正当化するものとみなして、[ 20 ]イギリスの哲学者ジョン・スチュアート・ミルはコントの実証主義を歓迎したが、科学法則は想起または修正されやすいと考え、ミルもコントの『人間の宗教』には関与しなかった。コントは科学法則をすべての知識の反駁できない基盤として扱うことに自信を持ち、著名な科学者を称える教会は、社会学（コントが造語）を通じて人類の社会福祉のために科学を適用するために公衆の意識を利他主義に集中させるべきだと信じた。

1830年代から1840年代にかけて、コントとミルが科学哲学の主導的な存在であった一方で、ウィリアム・ヒューウェルは列挙的帰納法がそれほど説得力がないと考え、帰納主義が優勢であったにもかかわらず、「重ね帰納法」を提唱した。[ 21 ]ヒューウェルは、「帰納法 という用語の特異な意味を認識すべきである」と主張した。「事実に重ねて帰納される概念が存在する」、つまり「あらゆる帰納的推論において新たな概念が発明される」ということである。概念の創造は見落とされやすく、ヒューウェル以前にはほとんど認識されていなかった。[ 21 ]ヒューウェルは次のように説明した。

「我々は事実に新たな概念を重ね合わせることで事実を結びつけるが、この概念は一度導入され適用されると、事実と不可分に結びつき、必然的に事実に内包されているとみなされる。概念によって一旦事実が心の中で結び付けられると、人々はもはや、事実が結び付けられる前の、ばらばらで支離滅裂な状態にそれらを容易に戻すことはできない。」[ 21 ]

これらの「過剰誘導」的説明には欠陥があるかもしれないが、ヒューウェルがコンシリエンス（共感覚）と呼んだもの、すなわち複数の領域における帰納的一般化を同時に予測する能力を示すことで、その正確性が示唆される。ヒューウェルによれば、この能力によって説明の真偽が証明されるという。おそらく、科学を帰納主義的方法論と見なす当時の一般的な見解に合わせるためか、ヒューウェルは「帰納法」に数章を割き、帰納法には規則がなく訓練も不可能であるにもかかわらず、「帰納の論理」という表現を時折用いた。[ 21 ]

1870年代、プラグマティズムの創始者であるC.S.パースは、演繹的推論が数学的証明として基礎づけられることを広範な研究によって明らかにしました（ゴットロープ・フレーゲも独立して同様の研究を行いました）。パースは帰納法を認めていましたが、常に第三の推論の種類を主張し、それをアブダクション、レトロダクション、仮説、推定などと呼びました。[ 28 ] 後の哲学者たちは、パースのアブダクションなどを最善の説明への推論（IBE）と呼びました。[ 29 ]

現代哲学

バートランド・ラッセル

ジョン・メイナード・ケインズはヒュームの帰納法の問題を浮き彫りにし、その解答、あるいは彼が到達しうる限りの解決法として論理的確率を提示した。 [ 30 ]バートランド・ラッセルはケインズの『確率論』が帰納法の最良の研究であるとし、ジャン・ニコの『帰納法の論理的問題』やRBブレイスウェイトによる1925年10月号の『マインド』誌上のケインズの著作評と併せて読めば、「帰納法について知られていることのほとんど」を網羅できると考えた。ただし、この主題は「技術的で難解であり、かなりの数学を必要とする」ものであった。[ 31 ] 20年後、ラッセルはケインズに倣い、列挙的帰納法を「独立した論理原理」とみなした。[ 32 ] [ 33 ] [ 34 ] ラッセルは以下を発見した。

ヒュームの懐疑主義は、帰納原理の拒絶に完全に基づいている。因果関係に適用される帰納原理は、AがBを伴って、あるいはBに続いて起こることが非常に多い場合、次にAが観察される機会にも、Bが伴って、あるいはBに続いて起こる可能性が高い、と述べている。この原理が妥当であるためには、十分な数の事例によって、その確率が確実性に大きく近づかなければならない。この原理、あるいはこの原理を導き出す他の原理が真であるならば、ヒュームが拒絶する偶発的な推論は、確実性を与えるという点ではなく、実用上十分な確率を与えるという点において、妥当である。この原理が真でないならば、特定の観察から一般的な科学法則を導き出そうとするあらゆる試みは誤りであり、経験主義者にとってヒュームの懐疑主義は避けられない。もちろん、この原理自体は、観察された均一性から循環論法なしに推論することはできない。なぜなら、そのような推論を正当化するためには、この原理が必要とされるからである。したがって、この原理は、あるいは…でなければならない。経験に基づかない独立した原理から演繹される。この点において、ヒュームは純粋経験主義は科学の十分な基盤ではないことを証明した。しかし、この一つの原理が認められれば、他のすべては、我々の知識はすべて経験に基づいているという理論に従って進むことができる。これは純粋経験主義からの重大な逸脱であり、経験主義者でない者は、なぜ一つの逸脱が認められるなら他の逸脱は禁じられるのかと問うかもしれない。しかし、これらはヒュームの議論によって直接提起された疑問ではない。これらの議論が証明しているのは――そして私はその証明に反論することはできないと思うが――帰納法は独立した論理原理であり、経験からも他の論理原理からも演繹することができず、この原理なしには科学は不可能であるということなのだ。[ 34 ]

ギルバート・ハーマン

1965年の論文で、ギルバート・ハーマンは、列挙的帰納法は自律的な現象ではなく、単に最善の説明への推論（IBE）の隠された結果であると説明しました。[ 29 ] IBEは、 C・S・パースのアブダクション と同義です。[ 29 ]科学的実在論 を支持する多くの科学哲学者は、IBEは科学者が自然に関するほぼ真の科学理論を展開する方法であると主張してきました。[ 35 ]

演繹的推論との比較

議論の用語

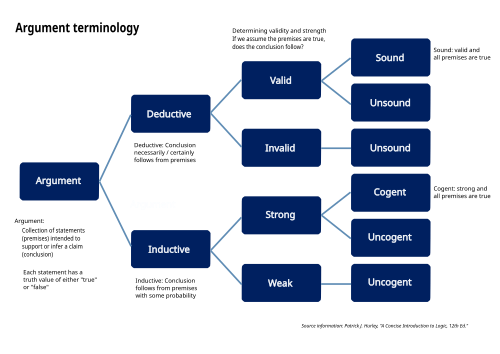
帰納的推論は、演繹的推論とは対照的に、前提がすべて真であっても結論が偽となる可能性を許容する議論の一形態である。 [ 36 ]演繹的推論と帰納的推論のこの違いは、演繹的議論と帰納的議論を説明する際に用いられる用語に反映されている。演繹的推論において、議論の前提が真であると仮定すれば、結論も必ず真となる場合、その議論は「妥当」である。議論が妥当であり、前提も真であれば、その議論は「健全」である。一方、帰納的推論において、議論の前提は結論が必ず真となることを決して保証することはできない。むしろ、議論の前提が真であると仮定すれば、結論がおそらく真となる場合、その議論は「強い」と言える。議論が強く、前提が真であると考えられる場合、その議論は「説得力がある」と言われる。[ 37 ]より形式的には、帰納的議論の結論は「蓋然性が高い」「もっともらしい」「可能性が高い」「合理的」「正当化される」などと言われることはあっても、「確実」や「必然的」などと言われることは決してない。論理は蓋然性から確実性への橋渡しをしない。

ある程度の臨界確率を通して確実性を得ることの無益さは、コイン投げの例で説明できます。誰かがコインが表か裏かを試したとします。コインを10回投げると、10回とも表が出ます。この時点で、表が出ていると信じる強い理由があります。何と言っても、10回連続で表が出る確率は0.000976、つまり1000分の1未満です。そして、100回投げた後、すべて表が出ました。これでコインが表であることは「事実上」確実となり、コインがおそらく表であるということは「真実」であるとみなすことができます。それでも、次に投げたときに裏が出る可能性を論理的にも経験的にも排除することはできません。何度連続して表が出ても、この事実は変わりません。もし機械にコインを何度も投げ続けるようにプログラムすれば、ある時点で100回連続で表が出ることになるでしょう。時が満ちれば、あらゆる組み合わせが現れるでしょう。

公平なコインで10回中10回表が出る可能性は極めて低い（この結果がコインに偏りがあるように見える原因となっている）という点についてですが、表と裏が連続して出る確率はどれも同じくらい低い（例えばHHTTHTHHHT）にもかかわらず、 10回投げるたびに必ず発生するという事実に驚く人は多いでしょう。つまり、 10回投げた結果はすべて、10回中10回表が出る確率と同じで、0.000976です。表と裏の連続を記録しておけば、どのような結果であっても、まさにその連続の確率は0.000976でした。

前提が与えられれば結論が必然的に導かれる場合、その議論は演繹的である。つまり、前提が真であれば結論も必ず真である。例えば、10回連続で表が出た後、コインがおそらく両面であるとみなされるための統計的基準を満たしていると推論するかもしれない。この結論は、次にコインを投げて裏が出ても反証にならない。

演繹的結論がその前提から正当に導かれる場合、それは有効です。そうでなければ、それは無効です（議論が無効であるということは、その結論が偽であるということではなく、前提のせいで正しい結論が得られないというだけのことです）。以下の例を見れば、前提と結論の関係は、結論の真理性が既に前提に暗黙的に含まれているということがわかるでしょう。独身者は独身であると私たちが言うから、つまり私たちがそう定義したからです。ソクラテスは死ぬべき存在です。なぜなら、私たちが彼を死ぬべき存在の集合に含めたからです。有効な演繹的議論の結論は、その真理性が厳密に論理的関係の問題であるため、既に前提に含まれています。結論は前提以上のことを言うことはできません。一方、帰納的前提は事実と証拠からその内容を引き出し、それに応じて結論は事実に基づく主張または予測を行います。その信頼性は証拠に比例して変化します。帰納は世界について何か新しいことを明らかにしようとします。帰納は前提に含まれる 以上のことを言おうとしていると言えるでしょう。

帰納的議論と演繹的議論の違いをより明確に理解するために、「これまで見てきたすべての長方形は4つの直角を持っているので、次に見る長方形も4つの直角を持つだろう」という表現は意味をなさないことを考えてみましょう。これは論理関係を事実であり発見可能なものとして扱い、したがって可変で不確実なものとして扱うことになります。同様に、演繹的に言えば、「すべてのユニコーンは飛ぶことができる。私にはチャーリーという名前のユニコーンがいる。したがってチャーリーは飛ぶことができる」という表現は許容されるかもしれません。この演繹的議論が妥当なのは、論理関係が成り立っているからであり、その事実の妥当性には関心がないからです。

帰納的推論の結論は本質的に不確実である。それは、前提が与えられた場合、何らかの証拠理論に従って結論がどの程度「信頼できる」かという点のみを扱う。例としては、多値論理、デンプスター・シェーファー理論、ベイズの定理などの推論規則を伴う確率論などが挙げられる。演繹的推論とは異なり、帰納的推論は結論を導くために閉領域に渡る普遍性に依存しないため、認識論的不確実性がある場合にも適用可能である（ただし、これには技術的な問題が生じる可能性がある。例えば、確率の第二公理は閉世界仮定である）。[ 38 ]

これら2種類の議論のもう一つの決定的な違いは、現実のような非公理的または経験的なシステムでは演繹的な確実性は不可能であり、そのようなシステムの（確率的）知識への主な手段として帰納的推論が残されるという点である。[ 39 ]

「 Aが真ならば、 B、C、Dも真となる」という仮定のもと、演繹の例としては「 Aは真であるから、 B、C、Dも真であると演繹できる」が挙げられます。帰納の例としては「B、C、Dが真であると観察されるから、Aも真である可能性がある」が挙げられます。Aは、 B、C、Dが真であることの合理的な説明となります。

例えば：

十分に大きな小惑星の衝突は非常に大きなクレーターを形成し、非鳥類型恐竜を絶滅に追い込む可能性のある厳しい衝突冬を引き起こします
メキシコ湾には、非鳥類型恐竜が絶滅した時期に非常に近い時期に作られた非常に大きなクレーターがあることがわかっています。
したがって、この衝突によって非鳥類型恐竜が絶滅した理由を説明できる可能性がある。

しかし、大量絶滅の原因が小惑星によるものだという説明は必ずしも正しいわけではないことに注意すべきである。地球の気候に影響を与える可能性のある他の出来事も、非鳥類型恐竜の絶滅と同時期に起こっている。例えば、インドのデカン高原の形成時に発生した火山ガス（特に二酸化硫黄）の放出などである。

帰納的議論のもう一つの例:

私たちが知るすべての生物は、存在するために液体の水に依存しています。
したがって、もし新しい生物的生命体が発見されたら、その存在はおそらく液体の水に依存することになるでしょう。

この議論は、新たな生物が発見されるたびに展開することができ、そのたびに正しい結論に至ったであろう。しかし、将来、液体の水を必要としない生物が発見される可能性は依然として存在する。その結果、この議論は次のように述べられるだろう。

私たちが知るすべての生物は、存在するために液体の水に依存しています。
したがって、すべての生物は、存在するために液体の水に依存していると考えられます。

「誤った」統計的三段論法の典型的な例は、ジョン・ヴィッカースによって提示されました。

私たちが見た白鳥はすべて白色でした。
したがって、私たちはすべての白鳥が白いことを「知っています」。

この結論は、当時知られていた白鳥の個体数が実際にはすべての白鳥を代表するものではなかったため、成り立たない。より合理的な結論は、適用可能な慣習に従えば、少なくとも短期的には、イングランドの白鳥はすべて白色であると 合理的に期待できる、というものである。

簡潔に言えば、演繹は確実性／必然性に関するものであり、帰納は確率に関するものである。[ 8 ]いかなる主張も、これら2つの基準のいずれかに当てはまる。推論分析におけるもう一つのアプローチは様相論理であり、これは可能とみなされる事柄の間の確率とは無関係に、必然性と 可能性の区別を扱う。

帰納的推論の哲学的定義は、個別的な事例からより広範な一般化へと​​単純に進行するよりも、より微妙なニュアンスを帯びています。むしろ、帰納的論理的議論の前提は、結論に対するある程度の支持（帰納的確率）を示唆するものの、結論を必然的に含意するものではありません。つまり、前提は真理を示唆するものの、それを保証することはありません。このように、一般的な言明から個別の事例（例えば、統計的三段論法）へと移行する可能性があります。

ここで述べる帰納的推論の定義は、実際には演繹的推論の一種である数学的帰納法とは異なることに注意されたい。数学的帰納法は、再帰的に定義された集合の性質の厳密な証明を提供するために使用される。[ 40 ]数学的帰納法の演繹的性質は、有限個の事例に基づく列挙的帰納法の手順（例えば、網羅的証明）の場合とは対照的に、非有限個の事例に基づくことに由来する。数学的帰納法と網羅的証明はどちらも完全帰納法の例である。完全帰納法は、仮面を被せられたタイプの演繹的推論である。

帰納法の問題

帰納的推論の不健全性は、ピュロン主義の哲学者セクストゥス・エンピリコスにまで遡る哲学者たちによって指摘されてきたが[ 41 ] 、帰納の問題に対する古典的な哲学的批判は、スコットランドの哲学者デイヴィッド・ヒュームによってなされた。[ 42 ]帰納的推論の使用は相当な成功を収めているものの、その適用の正当性は疑問視されてきた。このことを認識したヒュームは、我々の心は比較的限られた経験から、一見正しいように見えても実際には確実とはほど遠い結論を導き出すことが多いという事実を強調した。演繹では、結論の真理値は前提の真理性に基づく。しかし、帰納では、結論が前提に依存するかどうかは常に不確実である。例えば、すべてのワタリガラスは黒いと仮定しよう。黒いワタリガラスが多数いるという事実は、この仮定を裏付けている。しかし、白いワタリガラスがいることが発見されると、この仮定は無効になる。したがって、「すべてのカラスは黒い」という一般的な規則は、決して確実なものではない。ヒュームはさらに、帰納的推論を正当化することは不可能であると主張した。これは、帰納的に正当化できないため、帰納的に正当化するしかないからである。この議論は循環論法であるため、ヒュームは自身のフォークを用いて、帰納法の使用は論理的に正当化できないと結論付けた。[ 43 ]

ヒュームは、たとえ帰納法が信頼できないと証明されたとしても、我々は依然としてそれに頼らざるを得ないと述べた。そのため、ヒュームは厳格な懐疑主義の立場ではなく、帰納法の必然性を認める常識に基づく実践的懐疑主義を主張した。 [ 44 ]バートランド・ラッセルは、毎朝欠かさず餌を与えられ、帰納法の法則に従った鶏が、この餌やりは農夫に喉を切られるまでずっと続くと結論づけるという物語で、ヒュームの懐疑主義を説明した。[ 45 ]

1963年、カール・ポパーは「帰納法、すなわち多くの観察に基づく推論は神話である。それは心理学的事実でも、日常生活の事実でも、科学的手続きの一つでもない」と書いた。[ 46 ] [ 47 ] ポパーの1972年の著書『客観的知識』は、第1章が帰納法の問題に捧げられており、「私は主要な哲学的問題、すなわち帰納法の問題を解決したと思う」という一文で始まる。[ 47 ]ポパーの図式では、列挙的帰納法は、問題転換の際に推測と反駁の段階によって生み出される「一種の錯覚」である。[ 47 ]想像 力の飛躍である暫定的な解決策は即興であり、それを導く帰納法の規則を欠いている。[ 47 ] 結果として得られる制限のない一般化は演繹的であり、すべての説明的考察の必然的な帰結である。[ 47 ] しかし、ポパーの仮説的解決策は一般的に受け入れられず、論争は続いた。[ 48 ]

ドナルド・A・ギリーズは、帰納的推論に関連する推論のルールは科学に圧倒的に欠けていると主張し、ほとんどの科学的推論は「人間の創意工夫と創造力によって考え出された推測を伴うものであり、決して機械的な方法で推論されたり、厳密に指定されたルールに従って推論されたりしたものではない」と述べています。 [ 49 ]ギリーズはまた、「 AIの機械学習プログラム」という稀な反例を示しています。[ 49 ]

バイアス

帰納的推論は、結論が最新の知識と予測に基づいているため、仮説構築とも呼ばれます。演繹的議論と同様に、バイアスは帰納的議論の適切な適用を歪め、推論者が手がかりに基づいて最も論理的な結論を導き出すことを妨げる可能性があります。これらのバイアスの例としては、 利用可能性ヒューリスティック、確証バイアス、 予測可能世界バイアスなどが挙げられます

利用可能性ヒューリスティックは、推論者が容易に入手可能な情報に主に依存するようにすると考えられています。人々は、周囲の世界で容易にアクセスできる情報に頼る傾向があります。例えば、調査で様々な原因で死亡した人の割合を推定するよう求められた場合、ほとんどの回答者は、病気や交通事故といった、周囲の世界でそれほど重視されていないため、個人にとって技術的に「アクセスしにくい」原因ではなく、テロ、殺人、飛行機事故といった、メディアで最も頻繁に取り上げられている原因を選択します。

確証バイアスは、仮説を否定するよりも肯定しようとする自然な傾向に基づいています。研究により、人々は既知の仮説を反証しようとするよりも、それらの仮説とより一致する問題の解決策を探す傾向があることが示されています。実験では、被験者はしばしば、確立された仮説に適合する答えを求める質問をし、それによってそれらの仮説を確証します。例えば、サリーは社交的な人物であるという仮説が立てられた場合、被験者は当然、サリーが実際に社交的な人物であることを裏付けるような答えを導き出す質問をすることで、その前提を確証しようとします。

予測可能世界バイアスは、秩序が全く、あるいは特定の抽象レベルで存在することが証明されていない状況で、秩序を知覚する傾向に根ざしている。例えば、ギャンブルは予測可能世界バイアスの最も一般的な例の一つである。ギャンブラーはしばしば、結果に単純で明白なパターンを見ていると思い込み、目撃したことに基づいて結果を予測できると信じ始める。しかし実際には、これらのゲームの結果は予測が難しく、非常に複雑な性質を持っている。一般的に、人々は自分の信念や経験を説明したり正当化したりするために、ある種の単純な秩序を求める傾向があり、秩序に対する自分の知覚が真実とは全く異なる可能性があることに気づくのはしばしば難しい。[ 50 ]

ベイズ推論

ベイズ推論は信念理論というよりは帰納論理であり、どの信念が先験的に合理的であるかを決定するのではなく、証拠が提示された際に我々が持つ信念をどのように合理的に変更すべきかを決定する。まず、可能性の網羅的なリスト、それぞれの可能性の明確な確率的特徴づけ（尤度の観点から）、そしてそれらの正確な 事前確率（例えば、過去の経験からの論理または帰納に基づく）を検討する。そして証拠に直面した際には、ベイズ論理を用いて与えられた仮説に対する信念の強さを正確に調整し、「事後確率」候補を導き出す。この際、新たな証拠が我々の仮定を疑う具体的な理由をどの程度与えるかは考慮しない。そうでなければ、安定した状況に達するまで、必要に応じて可能性とその特徴づけの検討を見直し、繰り返すことが望ましい。[ 51 ]

帰納的推論

1960年頃、レイ・ソロモンオフは普遍帰納的推論の理論を創始しました。これは、観察に基づく予測理論であり、例えば、与えられた一連の記号に基づいて次の記号を予測する理論です。これは、アルゴリズム情報理論とベイズ理論の枠組みを組み合わせた形式的な帰納的枠組みです。普遍帰納的推論は確固たる哲学的基盤に基づいており、「ある程度複雑な環境や現実世界の環境を扱うには不十分なツールのように思われる」[ 52 ]。そして、数学的に形式化されたオッカムの剃刀と見なすことができます。この理論の基本的な要素は、 アルゴリズム的確率とコルモゴロフ複雑性の概念です

帰納的推論では通常、可算なサイズを持つ仮説クラスが考慮される。最近の進歩[ 53 ]により、帰納的推論の必要十分条件が確立された。すなわち、仮説クラスがオンライン学習可能クラスの可算な和集合である場合に限り、有限の誤差境界が保証される。注目すべきは、この条件により、仮説クラスが非可算なサイズであっても、この枠組み内で学習可能であり続けることができる点である。

参照

参考文献

  1. ^ Copi, IM; Cohen, C.; Flage, DE (2006). Essentials of Logic (Second ed.). Upper Saddle River, NJ: Pearson Education. ISBN 978-0-13-238034-8。
  2. ^ a bゴヴィア、トゥルーディ (2013). 『議論の実践的研究 強化版 第7版』 ボストン、マサチューセッツ州：Cengage Learning. p. 283. ISBN 978-1-133-93464-6。
  3. ^シャウムのアウトライン、論理学、第2版。ジョン・ノルト、デニス・ロハティン、アーチル・ヴァルジ著。マグロウヒル、1998年、223ページ
  4. ^シャウムのアウトライン、論理学、230ページ
  5. ^ジョンソン、デール・D.、ジョンソン、ボニー、ネス、ダニエル、ファレンガ、スティーブン・J. (2005). 『教師教育の矮小化：認定制度の逼迫』 ロウマン＆リトルフィールド. pp.  182–83 . ISBN 9780742535367。
  6. ^論理学入門。ゲンスラー、280ページ
  7. ^ロメイーン、JW (2004). 「仮説と帰納的予測：衝突データに関する例を含む」 ( PDF) . Synthese . 141 (3): 333–64 . doi : 10.1023/B:SYNT.0000044993.82886.9e . JSTOR 20118486. S2CID 121862013. 2020年10月24日時点のオリジナルからのアーカイブ(PDF) . 2020年8月22日閲覧  
  8. ^ a b論理学入門、ハリー・J・ゲンスラー、ラトレッジ、2002年、p. 268
  9. ^バロネット、スタン (2008). 『論理学』 アッパーサドルリバー、ニュージャージー州: ピアソン・プレンティス・ホール. pp.  321–25 .
  10. ^類推による推論の詳細については、 Juthe, 2005 （Wayback Machineで2009年3月6日にアーカイブ）を参照してください。
  11. ^論理体系。ミル 1843/1930。333ページ
  12. ^ a b cハンター、ダン（1998年9月）「単一事例の荒野は存在しない：法における帰納的推論」法教育ジャーナル48（3）：370-72。
  13. ^ a b c J.M., Bochenski (2012). Caws, Peter (ed.). The Methods of Contemporary Thought . Springer Science & Business Media. pp.  108– 09. ISBN 978-94010357812020年6月5日閲覧
  14. ^チャーチル、ロバート・ポール (1990). 『論理学入門』（第2版）. ニューヨーク: セント・マーチンズ・プレス. p. 355. ISBN 978-0-312-02353-9. OCLC  21216829 .典型的な列挙的帰納法では、前提として共通の性質を持つと観察された個体を列挙し、結論として同じ集団のすべての個体がその性質を持つと主張します。
  15. ^シャウムのアウトライン、論理学、pp. 243–35
  16. ^ a b cグッドイナフ, ジョン・B.、ウェインストック, チャールズ・B.、クライン, アリ・Z. (2013). 「エリミネーティブ・インダクション：システムの信頼性を論じるための基礎」. 2013 第35回国際ソフトウェア工学会議 (ICSE) . pp.  1161– 1164. doi : 10.1109/ICSE.2013.6606668 . ISBN 978-1-4673-3076-3– IEEE経由
  17. ^ロブ・ホッペ、ウィリアム・N・ダン (2001).環境政策分析における知識、権力、参加. Transaction Publishers. p. 419. ISBN 978-1-4128-2721-8。
  18. ^シュム、デイビッド・A. (2001). 『確率的推論の証拠的基礎』エバンストン、イリノイ州：ノースウェスタン大学出版局、32ページ。ISBN 0-8101-1821-1。
  19. ^ホッジ、ジョナサン、ホッジ、マイケル、ジョナサン・セッションズ、ラディック、グレゴリー (2003). 『ケンブリッジ・コンパニオン・トゥ・ダーウィン』ケンブリッジ：ケンブリッジ大学出版局.  174ページ. ISBN 0-521-77197-8。
  20. ^ a b cウェズリー・C・サーモン、「自然の均一性」、 2018年8月18日アーカイブ、Wayback Machine、哲学と現象学的研究、1953年9月; 14 (1):39–48、[39]
  21. ^ a b c d e Roberto Torretti, The Philosophy of Physics (Cambridge: Cambridge University Press , 1999), 219–21 Archived 9 May 2022 at the Wayback Machine [216] Archived 9 May 2022 at the Wayback Machine .
  22. ^ a bステファノ・ガッテイ『カール・ポパーの科学哲学：基盤なき合理性』（ニューヨーク：ラウトレッジ、2009年）、第2章「科学と哲学」、28～30頁。
  23. ^タレブ、ナシム・ニコラス（2010年）『ブラック・スワン：第二版：極めてあり得ない脆弱性の影響』ランダムハウス出版、ニューヨーク、199、302、383頁。ISBN 978-0812973815。
  24. ^ガレノス『医学経験論』、24ページ
  25. ^ Plutynski, Anya (2011). 「アブダクションの4つの問題：簡潔な歴史」 . HOPOS: 国際科学哲学史協会誌. 1 (2): 227– 248. doi : 10.1086/660746 . S2CID 15332806. 2023年4月11日時点のオリジナルよりアーカイブ。2022年4月16日閲覧。 
  26. ^マコーリフ、ウィリアム・HB (2015). 「アブダクションはどのようにして最善の説明への推論と混同されたのか？」 .チャールズ・S・パース協会紀要. 51 (3): 300– 319. doi : 10.2979/trancharpeirsoc.51.3.300 . ISSN 0009-1774 . JSTOR 10.2979/trancharpeirsoc.51.3.300 . S2CID 43255826. 2022年4月16日時点のオリジナルよりアーカイブ。2022年4月16日閲覧。   
  27. ^参照：カント『イマヌエル』（1787年）。『純粋理性批判』pp. B132。
  28. ^ Roberto Torretti, The Philosophy of Physics (Cambridge: Cambridge University Press , 1999)、 226頁Archived 9 May 2022 at the Wayback Machine、 228–29頁Archived 9 May 2022 at the Wayback Machine。
  29. ^ a b cテッド・ポストン「基礎主義」Wayback Machineで2019年9月26日にアーカイブ、§ b「適切な推論の理論」、§§ iii「リベラル帰納主義」、インターネット哲学百科事典、2010年6月10日（最終更新）：厳密な帰納主義は、認識論的に基本的な信念からの演繹的推論では対応できない、世界についてのある種の推論的知識が我々にはあるという考えに基づいています。厳密な帰納主義の利点については、ごく最近議論が巻き起こっています。一部の哲学者は、列挙的帰納のモデルに当てはまらない、他の非演繹的推論の形態があると主張しています。C.S . パースは「アブダクション」または「最善の説明への推論」と呼ばれる推論の形態について説明しています。この形式の推論は、説明的考察を用いて信念を正当化します。例えば、2人の学生がコピーしたと推論します。利用可能なデータに対する最良の説明だからという理由で、3人目からの回答を受け入れるとします。彼らはそれぞれ同じ間違いを犯しており、2人は3人目から見てその通りでした。あるいは、より理論的な文脈では、ブラウン運動に対する最良の説明だから、非常に小さな観測不可能な粒子が存在すると推論します。列挙帰納法とは異なる、最良の説明への推論形式の正当性を認める見解を「リベラル帰納主義」と呼ぶことにします。リベラル帰納主義の擁護については、ギルバート・ハーマンの古典的な論文（1965年）を参照してください。ハーマンは、列挙帰納法は最良の説明への推論の偽装された形式にすぎないとする、リベラル帰納主義の強力なバージョンを擁護しています。
  30. ^デイヴィッド・アンドリュース『ケインズとイギリスのヒューマニストの伝統：市場の道徳的目的』（ニューヨーク：ラウトレッジ、2010年）、 63～65頁。
  31. ^ラッセル、バートランド (1927). 『哲学概論』 ロンドンおよびニューヨーク: アレン・アンド・アンウィン.バートランド・ラッセル著『バートランド・ラッセル基本著作集』（ニューヨーク：ラウトレッジ、2009年）「推論の妥当性」157～164ページ、159ページの引用。2022年5月9日アーカイブ、Wayback Machineにて。
  32. ^ラッセル 1948年、396～450頁。harvnb エラー: ターゲットなし: CITEREFRussell1948 (ヘルプ)
  33. ^ Gregory Landini, Russell (New York: Routledge, 2011)、p. 230。Wayback Machineで2022年5月9日にアーカイブ。
  34. ^ a bバートランド・ラッセル『西洋哲学史』（ロンドン：ジョージ・アレン・アンド・アンウィン、1945年 / ニューヨーク：サイモン・アンド・シュスター、1945年）、673-74頁。
  35. ^ Stathis Psillos、「ヴァン・フラーセンのアブダクション推論批判について」 2018年8月18日アーカイブ、 Philosophical Quarterly 、 1996年1月; 46 (182):31–47、[31]。
  36. ^ジョン・ヴィッカーズ『帰納法の問題』、Wayback Machineで2014年4月7日にアーカイブ。スタンフォード哲学百科事典。
  37. ^ Herms, D. 「科学研究における仮説検定の論理的根拠」(PDF) 。 2009年3月19日時点のオリジナル(PDF)からアーカイブ。 2005年7月24日閲覧。
  38. ^ Kosko, Bart (1990). 「あいまいさ対確率」. International Journal of General Systems . 17 (1): 211–40 . Bibcode : 1990IJGS...17..211K . doi : 10.1080/03081079008935108 .
  39. ^ 「カントの理性に関する説明」スタンフォード哲学百科事典：カントの理性に関する説明スタンフォード大学形而上学研究所、2018年。2015年12月8日時点のオリジナルよりアーカイブ。 2015年11月27日閲覧。
  40. ^ Chowdhry, KR (2015). 『離散数学構造の基礎（第3版）』 PHI Learning Pvt. Ltd. p. 26. ISBN 978-81203507482016年12月1日閲覧
  41. ^セクストゥス・エンピリクス『ピュロン主義の概要』、 RGバリー訳、ハーバード大学出版局、マサチューセッツ州ケンブリッジ、1933年、283ページ。
  42. ^デイヴィッド・ヒューム(1910) [1748]. 『人間の理解に関する探求』 PFコリアー＆サン. ISBN 978-0-19-825060-92007年12月31日時点のオリジナルよりアーカイブ。2007年12月27日閲覧{{cite book}}：ISBN / 日付の非互換性（ヘルプ）
  43. ^ヴィッカース、ジョン.「帰納法の問題」ウェイバックマシンで2014年4月7日にアーカイブ（第2節）.スタンフォード哲学百科事典. 2010年6月21日
  44. ^ヴィッカース、ジョン.「帰納法の問題」、 2014年4月7日アーカイブ、Wayback Machine（セクション2.1）.スタンフォード哲学百科事典. 2010年6月21日.
  45. ^ラッセル、バートランド (1997). 『哲学の問題』 オックスフォード: オックスフォード大学出版局. p. 66. ISBN 978-0195115529。
  46. ^ポッパー、カール・R.；ミラー、デイヴィッド・W. (1983). 「帰納的確率の不可能性についての証明」. Nature . 302 ( 5910): 687–88 .書誌コード: 1983Natur.302..687P . doi : 10.1038/302687a0 . S2CID 4317588 
  47. ^ a b c d eドナルド・ギリーズ、「問題解決と帰納法の問題」『ポパー再考』 （ドルドレヒト：シュプリンガー、2009年）、ズザナ・パルスニコバ＆ロバート・S・コーエン編、pp. 103–05。
  48. ^第5章「帰納的論理をめぐる論争」 、リチャード・マテッシッチ編『器械的推論とシステム方法論：応用科学と社会科学の認識論』（ドルドレヒト： D. ライデル出版、1978年）、 141～143ページ。Wayback Machineに2022年5月9日アーカイブ。
  49. ^ a bドナルド・ギリーズ、「問題解決と帰納法の問題」、ズザナ・パルスニコバ＆ロバート・S・コーエン編『ポパー再考』（ドルドレヒト：シュプリンガー、2009年）、113ページ。 111 2022年5月9日アーカイブWayback Machine：「私は以前、帰納的推論の規則は存在しないというポパーの主張にはいくつかの例外があると主張しました。しかし、これらの例外は比較的まれです。例えば、AIの機械学習プログラムに見られます。過去と現在における人間の科学の大部分には、帰納的推論の規則は存在しません。そのような科学においては、ポパーの推測モデルは、自由に考案され、検証されるものであり、帰納的推論に基づくいかなるモデルよりも正確であるように思われます。確かに、今日では人間が行う科学の文脈において「最善の説明への推論」や「帰納的推論」という言葉が使われていますが、そのようないわゆる推論は、演繹的推論規則のような厳密に定式化された規則に基づく推論とは全く異なります。例えば、「最善の説明への推論」や「帰納的推論」について語る人々は、演繹的推論規則のような厳密に定式化された規則に基づく推論を決して定式化しません。これらのいわゆる推論が行われる場所。実際には、彼らが例に挙げている「推論」は、人間の創意工夫と創造力によって考え出された推測であり、決して機械的な方法で、あるいは厳密に規定された規則に従って推論されたものではない。
  50. ^グレイ、ピーター（2011年）『心理学』（第6版）ニューヨーク：ワース。ISBN 978-1-4292-1947-1。
  51. ^アーヴィング・J・グッド (1983). 『グッド・シンキング：確率の基礎とその応用』（ドーバー、ニューヨーク、2009年複製版）。ミネアポリス：ミネアポリス大学出版局。pp.  ix– xvii, 18, 27, 29, 36– 38, 123– 127
  52. ^ラスマナー, サミュエル;フッター, マーカス(2011). 「普遍帰納法の哲学的論文」 .エントロピー. 13 (6): 1076–136 . arXiv : 1105.5721 . Bibcode : 2011Entrp..13.1076R . doi : 10.3390/e13061076 . S2CID 2499910 . 
  53. ^ Lu, Z. (2024). 「帰納的推論はいつ可能になるか？」 NeurIPS 2024 .

さらに読む

無料辞書『ウィクショナリー』で「帰納的推論」を調べてください
Wikisource には、1920 年のアメリカ百科事典の帰納的推論に関する記事のテキストがあります。
「 https://en.wikipedia.org/w/index.php?title=Inductive_reasoning&oldid=1329426629」より引用