自然数オブジェクト

圏論において、自然数オブジェクト（NNO ）は、自然数と同様の再帰構造を備えたオブジェクトです。より正確には、終端オブジェクト1を持つ圏Eにおいて、NNO Nは次のように与えられます

1. グローバル要素z  : 1 → N、および
2. 矢印s  : N → N、​

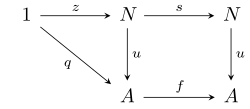
Eの任意のオブジェクトA、グローバル要素q  : 1 → A、矢印f  : A → Aに対して、次の条件を満たす唯一の矢印u  : N → Aが存在する:

1. u ∘ z = q、そして
2. u ∘ s = f ∘ u。^{[ 1 ] [ 2 ] [ 3 ]}

つまり、次の図の三角形と正方形は可換です。

ペア ( q , f ) はuの再帰データと呼ばれることもあり、再帰定義の形式で与えられます。

1. ⊢ u ( z ) = q
2. y ∈ _E N ⊢ u ( s y ) = f ( u ( y ))

上記の定義はNNOの普遍的性質であり、正準同型性まで 定義されることを意味します。上記で定義された矢印uが存在するだけでよい場合、つまり一意性が要求されない場合、Nは弱いNNOと呼ばれます。

同値な定義

直角閉圏（CCC）またはトポイにおけるNNOは、次のように同値に定義されることがあります（ローヴェレによる）。すべての矢印のペアg  : A → Bとf  : B → Bに対して、次の図の正方形が交換するような唯一のh  : N × A → Bが存在する。 ^{[ 4 ]}

これと同じ構成により、カルティシアン閉でないカルティシアン カテゴリ内の弱い NNO が定義されます。

終端オブジェクト 1 と二項余積（ + で表記）を持つカテゴリでは、NNO はX ↦ 1 + Xによってオブジェクトに作用し、 f ↦ id ₁ + fによって矢印に作用する自己関数の初期代数として定義できます。^{[ 5 ]}

特性

• すべてのNNOは、次の形式の図式圏の始対象である

${\displaystyle 1{\xrightarrow {~\quad q\quad ~}}A{\xrightarrow {~\quad f\quad ~}}A}$

• デカルト閉カテゴリに弱い NNO がある場合、そのカテゴリのすべてのスライスにも弱い NNO が存在します。
• NNOは、解析学の非標準モデルと同様に、型理論の非標準モデルにも適用できます。このようなカテゴリ（またはトポス）は、「無限に多くの」非標準自然数を持つ傾向があります。（いつものように、非標準NNOを得る簡単な方法があります。例えば、 z = szの場合、カテゴリまたはトポスEは自明です。）
• Freyd は、 zとs がNNO の共積図を形成することを示しました。また、 ! _N  : N → 1 はsと 1 _Nの共等化子です。つまり、 Nのグローバル要素のすべてのペアはsによって接続されています。さらに、この 2 つの事実はすべての NNO を特徴付けます。

例

• 集合の圏であるSetにおいて、標準的な自然数はNNOです。^{[ 6 ]} Setの終端オブジェクトはシングルトンであり、シングルトンからの関数は集合の単一の要素を取り出します。自然数𝐍はNNOです。ここで、zはシングルトンから𝐍への関数で、その像は0であり、sは後続関数です。（実際には、 zが𝐍の任意の要素を取り出すことを許可し、結果として得られるNNOはこのNNOと同型になります。）定義の図が可換であることは、数学的帰納法を用いて証明できます
• マルティン＝レーフ型理論の型の圏（型をオブジェクト、関数を矢印とする）において、標準的な自然数型natは NNO である。nat の再帰子を用いることで、適切な図式が可換であることを示すことができる。
• が終端対象を持つグロタンディーク・トポスであり、カテゴリ 上の何らかのグロタンディーク位相に対して であると仮定する。すると、が 上の定数前層であるとき、 における NNO はの層化であり、 の形をとることが示される。${\displaystyle {\mathcal {E}}}$ ${\displaystyle \top}$ ${\displaystyle {\mathcal {E}}\simeq \mathbf {Shv} ({\mathfrak {C}},J)}$ ${\displaystyle J}$ ${\displaystyle {\mathfrak {C}}}$ ${\displaystyle \Gamma _{\mathbb {N} }}$ ${\displaystyle {\mathfrak {C}}}$ ${\displaystyle {\mathcal {E}}}$ ${\displaystyle \Gamma _{\mathbb {N} }}$ $${\displaystyle \mathbb {N} _{\mathcal {E}}\cong \left(\Gamma _{\mathbb {N} }\right)^{++}\cong \coprod _{n\in \mathbb {N} }\top .}$$

参照

• ペアノの算術公理
• 圏論的論理

参考文献

1. Johnstone 2002 , A2.5.1.
2. Lawvere 2005 , p. 14
3. Leinster, Tom (2014). 「集合論の再考」. American Mathematical Monthly . 121 (5): 403– 415. arXiv : 1212.6543 . Bibcode : 2012arXiv1212.6543L . doi : 10.4169/amer.math.monthly.121.05.403 . S2CID  5732995 .
4. ジョンストン 2002、A2.5.2。
5. バー、マイケル、ウェルズ、チャールズ (1990).計算科学のための圏論. ニューヨーク: プレンティス・ホール. p. 358. ISBN 0131204866 OCLC  19126000
6. ^2002、108ページ

• ジョンストン、ピーター・T. (2002). 『象のスケッチ：トポス理論大全』オックスフォード：オックスフォード大学出版局. ISBN 0198534256 OCLC  50164783
• ウィリアム・ローヴェア (2005) [1964]. 「集合の圏の初等理論（長編版）解説付き」 . 『圏の理論と応用』再版. 11 : 1– 35

外部リンク

• セクション2.2でNNOについて議論しているロバート・ハーパーの講義ノート： https://www.cs.cmu.edu/~rwh/courses/hott/notes/notes_week3.pdf
• Clive Newstead によるn -Category Cafeのブログ投稿: https://golem.ph.utexas.edu/category/2014/01/an_elementary_theory_of_the_ca.html
• コンピュータ科学者Philip Wadlerによる、自己関数子の代数としてのデータ型に関するメモ: http://homepages.inf.ed.ac.uk/wadler/papers/free-rectypes/free-rectypes.txt
• nLabに関するメモ: https://ncatlab.org/nlab/show/ETCS