フェーザー

直列RLC回路と特定のωに対する位相器図の例。上図の矢印は位相器図（軸のない複素平面）に描かれた位相器です。下図の矢印は電圧の基準極性と電流の基準方向を示しており、混同しないように注意してください。

物理学と工学において、位相ベクトル（phase vector ^{[ 1 ] [ 2 ]}）は、振幅Aと初期位相θが時間不変で、角周波数ωが固定である正弦関数を表す複素数です。これは、より一般的な概念である解析表現と関連しており、^{[ 3 ]}解析表現は、正弦波を複素定数と時間と周波数に依存する係数の積に分解します。振幅と位相に依存する複素定数は、位相ベクトル（phaser）または複素振幅（complex amplitude）^{[ 4 ] [ 5 ]}、（古い文献では）正弦ベクトル（sinor ） ^{[ 6 ]} 、あるいは複素ベクトル（complexor ） ^{[ 6 ]}とも呼ばれています。

一般的な応用例としては、時間変動電流で駆動される電気回路網の定常解析が挙げられます。この解析では、すべての信号が共通の周波数を持つ正弦波であると仮定します。位相器表現を用いると、解析者は信号の振幅と位相を単一の複素数で表すことができます。これらの解析表現における唯一の違いは、複素振幅（位相器）です。このような関数の線形結合は、位相器（位相器演算または位相器代数^{[ 7 ] : 53} として知られる）と、それらすべてに共通する時間/周波数依存係数の線形結合として表すことができます。

フェーザという用語の起源は、ベクトルに可能なものと多少似た（図式的な）計算がフェーザでも可能であることを正しく示唆している。^{[ 6 ]}フェーザ変換の重要な追加機能は、正弦波信号（一定の振幅、周期、位相を持つ）の微分と積分が、フェーザ上の簡単な代数演算に対応することである。したがって、フェーザ変換により、時間領域で微分方程式（実係数を持つ）を解くのではなく、フェーザ領域で簡単な代数方程式（複素係数を持つ）を解くことで、 RLC回路のAC定常状態を分析（計算）することができる。^{[ 8 ] [ 9 ] [ a ]}フェーザ変換の考案者は、19世紀後半にゼネラル・エレクトリックで働いていたチャールズ・プロテウス・シュタインメッツである。 ^{[ 10 ] [ 11 ]}彼はオリバー・ヘヴィサイドからインスピレーションを得た。ヘヴィサイドの演算法は、変数pがjωとなるように修正された。複素数jは位相シフトという単純な意味を持つ。^{[ 12 ]}

いくつかの数学的な詳細を無視すると、位相器変換はラプラス変換（単一周波数に限定）の特殊なケースと見なすこともできます。これは、位相器表現とは対照的に、 RLC回路の過渡応答を（同時に）導くために使用できます。^{[ 9 ] [ 11 ]}しかし、ラプラス変換は数学的に適用するのがより難しく、定常状態解析のみが必要な場合、その努力は不当である可能性があります。^{[ 11 ]}

図2. 関数を複素平面で描くと、その虚数部と実数部からなるベクトルは原点を中心に回転します。その大きさはAで、2 π /ωごとに1周期となります。θは、 t = 0（およびnがすべての整数値の場合、 t = n 2 π / ω ）における正の実軸との角度です。${\displaystyle A\cdot e^{i(\omega t+\theta )}}$

表記

位相記号（角度記号とも呼ばれる）は、電子工学および電気工学において用いられる数学記号である。極座標が大きさで角度が^{[ 13 ]}と表記されるベクトルは、オイラーの公式に従って、ベクトルまたは複素数のいずれかを表すことができ、どちらも大きさは1である。 ${\displaystyle A}$ ${\displaystyle \theta}$ ${\displaystyle A\angle \theta .}$ ${\displaystyle 1\angle \theta }$ ${\displaystyle (\cos \theta ,\,\sin \theta )}$ ${\displaystyle \cos \theta +i\sin \theta =e^{i\theta }}$ ${\displaystyle i^{2}=-1}$

角度は度で表され、度からラジアンへの変換が暗黙的に行われます。例えば、ベクトルまたは数値であると想定されます。${\displaystyle 1\angle 90}$ ${\displaystyle 1\angle 90^{\circ },}$ ${\displaystyle (0,\,1)}$ ${\displaystyle e^{i\pi /2}=i.}$

複素数の乗算と除算は位相器記法によって簡単に表せる。ベクトルとが与えられれば、次が成り立つ。^{[ 14 ]}${\displaystyle v_{1}=A_{1}\angle \theta _{1}}$ ${\displaystyle v_{2}=A_{2}\angle \theta _{2}}$

${\displaystyle v_{1}\cdot v_{2}=A_{1}\cdot A_{2}\angle (\theta _{1}+\theta _{2})}$ 、

${\displaystyle {\frac {v_{1}}{v_{2}}}={\frac {A_{1}}{A_{2}}}\angle (\theta _{1}-\theta _{2})}$ 。

意味

一定の振幅、周波数、位相を持つ実数値正弦波は次の形式を持ちます。

${\displaystyle A\cos(\omega t+\theta ),}$

ここで、パラメータのみが時間変化します。虚数成分を含めると： ${\displaystyle t}$

${\displaystyle i\cdot A\sin(\omega t+\theta )}$

は、オイラーの公式に従って、リード段落で説明した因数分解の性質を与えます。

${\displaystyle A\cos(\omega t+\theta )+i\cdot A\sin(\omega t+\theta )=Ae^{i(\omega t+\theta )}=Ae^{i\theta }\cdot e^{i\omega t},}$

その実部は元の正弦波です。複素表現の利点は、他の複素表現との線形演算によって複素結果が得られ、その実部は他の複素正弦波の実部との同じ線形演算を反映することです。さらに、すべての計算は位相子だけで実行でき、共通因子は結果の実部の前に再挿入されます。 ${\displaystyle Ae^{i\theta },}$ ${\displaystyle e^{i\omega t}}$

関数は図2の解析的表現であり、複素平面上の回転ベクトルとして表されています。次の節で述べるように、 関数全体を位相ベクトルと呼ぶ方が便利な場合もあります^{[ 15 ] 。}${\displaystyle Ae^{i(\omega t+\theta )}}$ ${\displaystyle A\cos(\omega t+\theta ).}$

算術

定数（スカラー）による乗算

位相ベクトルに複素定数 を乗じると、別の位相ベクトルが生成されます。つまり、その効果は、基になる正弦波の振幅と位相を変化させることだけです。 ${\displaystyle Ae^{i\theta }e^{i\omega t}}$ ${\displaystyle Be^{i\phi }}$ $${\displaystyle {\begin{aligned}&\operatorname {Re} \left(\left(Ae^{i\theta }\cdot Be^{i\phi }\right)\cdot e^{i\omega t}\right)\\={}&\operatorname {Re} \left(\left(ABe^{i(\theta +\phi )}\right)\cdot e^{i\omega t}\right)\\={}&AB\cos(\omega t+(\theta +\phi )).\end{aligned}}}$$

電子工学において、は時間に依存しないインピーダンスを表します。特に、これは別の位相器の略記法ではありません。位相器電流にインピーダンスを乗じると、位相器電圧が生成されます。しかし、2つの位相器の積（または位相器の2乗）は、2つの正弦波の積を表し、これは新しい周波数成分を生成する非線形演算です。位相器表記法は、正弦波によって刺激される線形システムなど、1つの周波数を持つシステムのみを表すことができます。 ${\displaystyle Be^{i\phi }}$

追加

回転ベクトルの加算としての位相ベクトルの和

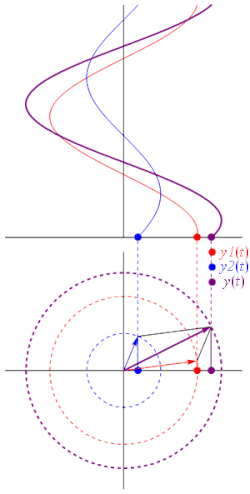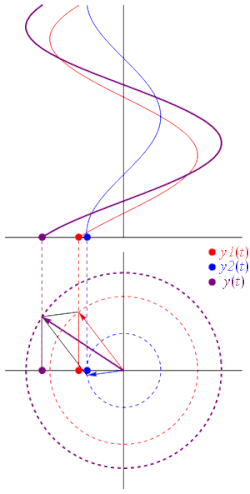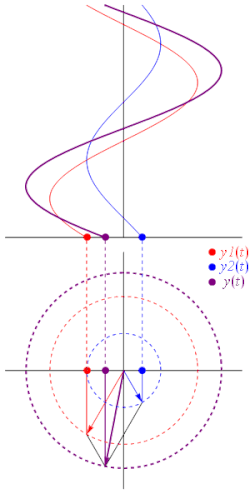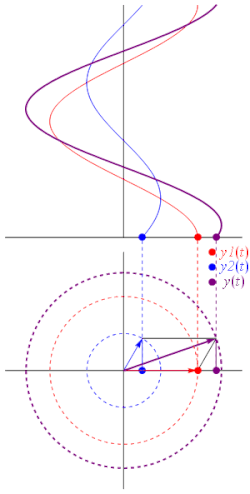
複数の位相ベクトルを足し合わせると、別の位相ベクトルが生成されます。これは、同じ周波数の正弦波を足し合わせると、その周波数の正弦波となるためです。 ここで、 $${\displaystyle {\begin{aligned}&A_{1}\cos(\omega t+\theta _{1})+A_{2}\cos(\omega t+\theta _{2})\\[3pt]={}&\operatorname {Re} \left(A_{1}e^{i\theta _{1}}e^{i\omega t}\right)+\operatorname {Re} \left(A_{2}e^{i\theta _{2}}e^{i\omega t}\right)\\[3pt]={}&\operatorname {Re} \left(A_{1}e^{i\theta _{1}}e^{i\omega t}+A_{2}e^{i\theta _{2}}e^{i\omega t}\right)\\[3pt]={}&\operatorname {Re} \left(\left(A_{1}e^{i\theta _{1}}+A_{2}e^{i\theta _{2}}\right)e^{i\omega t}\right)\\[3pt]={}&\operatorname {Re} \left(\left(A_{3}e^{i\theta _{3}}\right)e^{i\omega t}\right)\\[3pt]={}&A_{3}\cos(\omega t+\theta _{3}),\end{aligned}}}$$ $${\displaystyle A_{3}^{2}=(A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2})^{2}+(A_{1}\sin \theta _{1}+A_{2}\sin \theta _{2})^{2},}$$

そして、 とすると、 は次のようになります。 ${\textstyle \theta _{3}\in \left[-{\frac {\pi }{2}},{\frac {3\pi }{2}}\right]}$ ${\displaystyle \theta _{3}}$

• ${\textstyle \operatorname {sgn}(A_{1}\sin(\theta _{1})+A_{2}\sin(\theta _{2}))\cdot {\frac {\pi }{2}},}$ signum関数の場合;${\displaystyle A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}=0,}$ ${\displaystyle \operatorname {sgn} }$
• ${\displaystyle \arctan \left({\frac {A_{1}\sin \theta _{1}+A_{2}\sin \theta _{2}}{A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}}}\right),}$ もし;${\displaystyle A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}>0}$
• ${\displaystyle \pi +\arctan \left({\frac {A_{1}\sin \theta _{1}+A_{2}\sin \theta _{2}}{A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}}}\right),}$ もし。${\displaystyle A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}<0}$

あるいは、複素平面上の 余弦定理（または角度差の三角関数の恒等式）により、 $${\displaystyle A_{3}^{2}=A_{1}^{2}+A_{2}^{2}-2A_{1}A_{2}\cos(180^{\circ }-\Delta \theta )=A_{1}^{2}+A_{2}^{2}+2A_{1}A_{2}\cos(\Delta \theta ),}$$ ${\displaystyle \Delta \theta =\theta _{1}-\theta _{2}.}$

重要な点は、A ₃とθ _{3 が}ωやtに依存しないことです。これが位相ベクトル表記を可能にするのです。時間と周波数への依存性は、その間に別の位相ベクトルを生成する演算のみを使用する限り、抑制して結果に再挿入することができます。角度表記では、上記の演算は次のように書きます。 $${\displaystyle A_{1}\angle \theta _{1}+A_{2}\angle \theta _{2}=A_{3}\angle \theta _{3}.}$$

加算を別の観点から見ると、座標[ A 1 _cos ( ωt + θ ₁ ), A ₁ sin( ωt + θ ₁ )]と[ A ₂ cos( ωt + θ ₂ ), A ₂ sin( ωt + θ ₂ )] の2 つのベクトルがベクトル的に加算され、座標[ A ₃ cos( ωt + θ ₃ ), A ₃ sin( ωt + θ ₃ )]の結果のベクトルが生成されることになります(アニメーションを参照)。

完全に相殺的な干渉における3つの波の位相図

物理学では、このような加算は、正弦波が互いに干渉し合う（建設的または破壊的）ときに発生します。静的ベクトルの概念は、「3 つの同一の正弦波を完全に打ち消すには、どの程度の位相差が必要か」といった疑問に対する有用な洞察を提供します。この場合、単に長さの等しい 3 つのベクトルを取り、最後の頭が最初の尾と一致するように頭と尾を並べて配置することを想像してみてください。明らかに、これらの条件を満たす形状は正三角形であるため、各位相器と次の位相器間の角度は 120°（2 π ⁄ 3 ラジアン）、つまり波長λ ⁄ 3の 3 分の 1 になります。したがって、各波間の位相差も、三相電力の場合と同様に 120° である必要があります。

言い換えれば、これは次のことを示しています。 $${\displaystyle \cos(\omega t)+\cos \left(\omega t+{\frac {2\pi }{3}}\right)+\cos \left(\omega t-{\frac {2\pi }{3}}\right)=0.}$$

3つの波の例では、最初の波と最後の波の位相差は240°でしたが、2つの波では180°で相殺干渉が起こります。波の数が多い場合、相殺干渉が起こるためには位相子が円を描く必要があり、最初の位相子は最後の位相子とほぼ平行になります。つまり、多くの光源では、最初の波と最後の波の位相差が360度（波長1つ分）のときに相殺干渉が起こります。これが、単スリット回折において、遠端からの光が近端からの光よりも波長1つ分だけ遠くまで進んだ ときに極小値が発生する理由です。${\displaystyle \lambda }$

単一ベクトルが反時計回りに回転すると、点Aにあるベクトルの先端は360°、つまり2πラジアン回転し、1 周期を表します。ベクトルの先端の長さを、上図のように時間経過に応じて異なる角度間隔でグラフに投影すると、左から0時間目、つまりt = 0から経過した時間を表す正弦波が描かれます。ベクトルが水平の場合、ベクトルの先端は0°、180°、360°の角度を表します。

同様に、ベクトルの先端が垂直な場合、正のピーク値（+ A _max）は90°またはπ ⁄ 2で、負のピーク値（- A _max）は270°または3 π ⁄ 2で表されます。波形の時間軸は、位相器が移動した角度を度またはラジアンで表します。つまり、位相器は、ある時点（t）で「固定」された回転ベクトルのスケール化された電圧または電流値を表すと言えます。上記の例では、これは30°の角度です。

交流波形を解析する際には、特定の時点における交流量を表す位相器の位置を知る必要がある場合があります。特に、同じ軸上にある2つの異なる波形を比較したい場合などです。例えば、電圧と電流です。上記の波形では、波形が時刻t = 0に開始し、対応する位相角（度またはラジアン）が与えられていると仮定しています。

しかし、2つ目の波形がこのゼロ点の左または右から始まる場合、あるいは2つの波形の関係を位相器表記で表したい場合は、波形の位相差Φを考慮する必要があります。前回の位相差チュートリアルで使用した以下の図を考えてみましょう。

差別化と統合

位相ベクトルの時間微分または積分は別の位相ベクトルを生成する。 ^{[ b ]} 例えば： $${\displaystyle {\begin{aligned}&\operatorname {Re} \left({\frac {\mathrm {d} }{\mathrm {d} t}}{\mathord {\left(Ae^{i\theta }\cdot e^{i\omega t}\right)}}\right)\\={}&\operatorname {Re} \left(Ae^{i\theta }\cdot i\omega e^{i\omega t}\right)\\={}&\operatorname {Re} \left(Ae^{i\theta }\cdot e^{i\pi /2}\omega e^{i\omega t}\right)\\={}&\operatorname {Re} \left(\omega Ae^{i(\theta +\pi /2)}\cdot e^{i\omega t}\right)\\={}&\omega A\cdot \cos \left(\omega t+\theta +{\frac {\pi }{2}}\right).\end{aligned}}}$$

したがって、位相器表現では、正弦波の時間微分は定数による単なる乗算になります。 ${\textstyle i\omega =e^{i\pi /2}\cdot \omega }$

同様に、位相器の積分は、 による乗算に相当します。時間依存係数は影響を受けません。 ${\textstyle {\frac {1}{i\omega }}={\frac {e^{-i\pi /2}}{\omega }}.}$ ${\displaystyle e^{i\omega t},}$

線形微分方程式を位相器演算で解く場合、方程式のすべての項を因数分解して、それを解に再挿入するだけです。例えば、RC回路のコンデンサにかかる電圧に関する次の微分方程式を考えてみましょう。 ${\displaystyle e^{i\omega t}}$ $${\displaystyle {\frac {\mathrm {d} \,v_{\text{C}}(t)}{\mathrm {d} t}}+{\frac {1}{RC}}v_{\text{C}}(t)={\frac {1}{RC}}v_{\text{S}}(t).}$$

この回路の電圧源が正弦波の場合： $${\displaystyle v_{\text{S}}(t)=V_{\text{P}}\cdot \cos(\omega t+\theta ),}$$

代替できる${\displaystyle v_{\text{S}}(t)=\operatorname {Re} \left(V_{\text{s}}\cdot e^{i\omega t}\right).}$

$${\displaystyle v_{\text{C}}(t)=\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right),}$$ ここで、位相器と位相器は決定されるべき未知の量です。 ${\displaystyle V_{\text{s}}=V_{\text{P}}e^{i\theta },}$ ${\displaystyle V_{\text{c}}}$

位相器の略記法では、微分方程式は次のように簡約されます。 $${\displaystyle i\omega V_{\text{c}}+{\frac {1}{RC}}V_{\text{c}}={\frac {1}{RC}}V_{\text{s}}.}$$

導出

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right)+{\frac {1}{RC}}\operatorname {Re} (V_{\text{c}}\cdot e^{i\omega t})={\frac {1}{RC}}\operatorname {Re} \left(V_{\text{s}}\cdot e^{i\omega t}\right)}$

式1

これはすべての に対して成り立つはずなので、具体的には次のようになります。 ${\displaystyle t}$ ${\textstyle t-{\frac {\pi }{2\omega }},}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Im} \left(V_{\text{c}}\cdot e^{i\omega t}\right)+{\frac {1}{RC}}\operatorname {Im} \left(V_{\text{c}}\cdot e^{i\omega t}\right)={\frac {1}{RC}}\operatorname {Im} \left(V_{\text{s}}\cdot e^{i\omega t}\right).}$

式2

また、次のことも容易にわかります。 $${\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right)&=\operatorname {Re} \left({\frac {\mathrm {d} }{\mathrm {d} t}}{\mathord {\left(V_{\text{c}}\cdot e^{i\omega t}\right)}}\right)=\operatorname {Re} \left(i\omega V_{\text{c}}\cdot e^{i\omega t}\right)\\{\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Im} \left(V_{\text{c}}\cdot e^{i\omega t}\right)&=\operatorname {Im} \left({\frac {\mathrm {d} }{\mathrm {d} t}}{\mathord {\left(V_{\text{c}}\cdot e^{i\omega t}\right)}}\right)=\operatorname {Im} \left(i\omega V_{\text{c}}\cdot e^{i\omega t}\right).\end{aligned}}}$$

これらを式 1と式 2に代入し、式 2を掛けて両方の式を加算すると次のようになります。 ${\displaystyle i,}$ $${\displaystyle {\begin{aligned}i\omega V_{\text{c}}\cdot e^{i\omega t}+{\frac {1}{RC}}V_{\text{c}}\cdot e^{i\omega t}&={\frac {1}{RC}}V_{\text{s}}\cdot e^{i\omega t}\\\left(i\omega V_{\text{c}}+{\frac {1}{RC}}V_{\text{c}}\right)\!\cdot e^{i\omega t}&=\left({\frac {1}{RC}}V_{\text{s}}\right)\cdot e^{i\omega t}\\i\omega V_{\text{c}}+{\frac {1}{RC}}V_{\text{c}}&={\frac {1}{RC}}V_{\text{s}}.\end{aligned}}}$$

位相コンデンサ電圧を解くと次のようになります。 $${\displaystyle V_{\text{c}}={\frac {1}{1+i\omega RC}}\cdot V_{\text{s}}={\frac {1-i\omega RC}{1+(\omega RC)^{2}}}\cdot V_{\text{P}}e^{i\theta }.}$$

これまで見てきたように、係数の乗算は、振幅と位相の相対的な差を表し、${\displaystyle V_{\text{s}}}$ ${\displaystyle v_{\text{C}}(t)}$ ${\displaystyle V_{\text{P}}}$ ${\displaystyle \theta .}$

極座標形式では、最後の式の最初の項は次のようになります。 ここで、 。 $${\displaystyle {\frac {1-i\omega RC}{1+(\omega RC)^{2}}}={\frac {1}{\sqrt {1+(\omega RC)^{2}}}}\cdot e^{-i\phi (\omega )},}$$ ${\displaystyle \phi (\omega )=\arctan(\omega RC)}$

したがって： $${\displaystyle v_{\text{C}}(t)=\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right)={\frac {1}{\sqrt {1+(\omega RC)^{2}}}}\cdot V_{\text{P}}\cos(\omega t+\theta -\phi (\omega )).}$$

位相比

複素インピーダンスと呼ばれる量は2 つの位相器の比ですが、正弦波的に変化する関数に対応しないため、位相器ではありません。

アプリケーション

巡回法

位相器を使用すると、 DC回路を解く手法を線形AC回路の解に適用できます。^{[ a ]}

抵抗器に関するオームの法則

抵抗器には時間遅延がないため、信号の位相は変化せず、したがってV = IR は有効なままです。

抵抗器、インダクタ、コンデンサに関するオームの法則

V = IZ、ここでZは複素インピーダンスです。

キルヒホッフの回路法則

電圧と電流を複雑な位相器として扱います。

AC回路には、回路に流入する平均電力を表す有効電力（ P ）と、回路内を行き来する電力を表す無効電力（ Q ）があります。また、複素電力S = P + jQと、 Sの大きさを表す皮相電力を定義することもできます。位相ベクトルで表されるAC回路のべき乗法則は、S = VI ^*となります（ここで、I ^*はIの複素共役であり、電圧位相ベクトルVと電流位相ベクトルIの大きさは、それぞれ電圧と電流の RMS値です）。

これを踏まえて、抵抗回路の解析手法を位相器を用いて適用することで、抵抗器、コンデンサ、インダクタを含む単一周波数線形交流回路を解析することができる。多周波数線形交流回路や異なる波形を持つ交流回路を解析する場合、すべての波形を振幅と位相を持つ正弦波成分（フーリエ級数を使用）に変換し、重ね合わせ定理に従って各周波数を個別に解析することで、電圧と電流を求めることができる。この解法は、正弦波の入力と、すべての過渡現象が消えた後の定常状態にある解にのみ適用される。^{[ 16 ]}

この概念は電気インピーダンスを表す際によく用いられます。この場合、位相角とは、インピーダンスに印加される電圧とインピーダンスを流れる電流の 位相差のことです。

電力工学

三相交流電力システムの解析では、通常、位相ベクトルの集合は3つの複素立方根 1として定義され、0度、120度、240度の角度における単位振幅としてグラフィカルに表されます。多相交流回路の量を位相ベクトルとして扱うことで、平衡回路を簡略化し、不平衡回路を対称成分の代数的組み合わせとして扱うことができます。このアプローチにより、電圧降下、電力潮流、短絡電流などの電気計算に必要な作業が大幅に簡素化されます。電力システム解析の文脈では、位相角は度で、振幅は正弦波のピーク振幅ではなく RMS値で表すことがよくあります。

同期位相器の技術では、デジタル機器を用いて送電網内の広範囲の地点における送電系統電圧を表す位相器を測定します。位相器間の差は、電力潮流と系統の安定性を示します。

電気通信：アナログ変調

A: 振幅変調の位相器表現、B: 振幅変調の代替表現、C: 周波数変調の位相器表現、D: 周波数変調の代替表現

位相器を用いた回転フレーム画像は、振幅変調（およびその変種^{[ 17 ]}）や周波数変調などのアナログ変調を理解するための強力なツールとなり得る。

$${\displaystyle x(t)=\operatorname {Re} \left(Ae^{i\theta }\cdot e^{i2\pi f_{0}t}\right),}$$ ここで、括弧内の項は複素平面における回転ベクトルとして見られます。

位相器の長さは で、1 秒あたり 回転の速度で反時計回りに回転し、 の時点で正の実軸に対して の角度をなします。${\displaystyle A}$ ${\displaystyle f_{0}}$ ${\displaystyle t=0}$ ${\displaystyle \theta }$

波形は、このベクトルを実軸に投影したものとして見ることができます。変調波形は、この位相ベクトル（搬送波）と2つの追加の位相ベクトル（変調位相ベクトル）によって表されます。変調信号が （変調度、 は変調信号の周波数）の形式の単音である場合、振幅変調の場合、2つの変調位相ベクトルは次のように表されます。 ${\displaystyle x(t)}$ ${\displaystyle Am\cos {2\pi f_{m}t}}$ ${\displaystyle m}$ ${\displaystyle f_{m}}$

$${\displaystyle {1 \over 2}Ame^{i\theta }\cdot e^{i2\pi (f_{0}+f_{m})t},}$$ $${\displaystyle {1 \over 2}Ame^{i\theta }\cdot e^{i2\pi (f_{0}-f_{m})t}.}$$

2つの変調位相ベクトルは、そのベクトル和が常に搬送位相ベクトルと同位相となるように位相調整されている。別の表現としては、搬送位相ベクトルの端の周りを搬送位相ベクトルに相対的な速度で逆回転する2つの位相ベクトルがある。つまり、 ${\displaystyle f_{m}}$

$${\displaystyle {1 \over 2}Ame^{i\theta }\cdot e^{i2\pi f_{m}t},}$$ $${\displaystyle {1 \over 2}Ame^{i\theta }\cdot e^{-i2\pi f_{m}t}.}$$

周波数変調も同様の表現ですが、変調位相器が搬送波と同位相ではない点が異なります。この場合、変調位相器のベクトル和は搬送波の位相から90°シフトします。厳密には、周波数変調表現には、…などの小さな変調位相器が追加で必要ですが、実用上はこれらの影響が非常に小さいため、ほとんどの場合無視されます。 ${\displaystyle 2f_{m},3f_{m}}$

参照

• 同相成分と直交成分
  • 星座図
• 解析信号、時間によって変化する振幅、位相、周波数の位相器の一般化。
  • 複雑なエンベロープ
• 位相係数、単位振幅の位相器

脚注

1. AC回路の解析を含む。^{[ 7 ] : 53}
2. これは、複素指数が微分演算子の固有関数であることを意味すること。${\textstyle {\frac {d}{dt}}e^{i\omega t}=i\omega e^{i\omega t},}$

参考文献

1. Huw Fox、William Bolton (2002). 『エンジニアと技術者のための数学』 Butterworth-Heinemann. p.  30. ISBN 978-0-08-051119-1。
2. ( 2000). 『基本交流回路』（第2版）. ニューネス. p.  124. ISBN 978-0-08-049398-5。
3. ブレイスウェル、ロン著『フーリエ変換とその応用』マグロウヒル社、1965年、p269
4. KS Suresh Kumar (2008). 『電気回路とネットワーク』 . ピアソン・エデュケーション・インディア. p. 272. ISBN 978-81-317-1390-7。
5. Kequian Zhang; Dejie Li (2007).マイクロ波とオプトエレクトロニクスのための電磁気理論（第2版）. Springer Science & Business Media. p. 13. ISBN 978-3-540-74296-8。
6. J. Hindmarsh (1984).電気機械とその応用（第4版）. エルゼビア. p. 58. ISBN 978-1-4832-9492-6。
7. Gross, Charles A. (2012). 『電気工学の基礎』 Thaddeus Adam Roppel. ボカラトン、フロリダ州: CRC Press. ISBN 978-1-4398-9807-9. OCLC  863646311 .
8. William J. Eccles (2011). 『実用的な電気工学：基礎』 ​​Morgan & Claypool Publishers. p. 51. ISBN 978-1-60845-668-0。
9. リチャード・C・ドーフ、ジェームズ・A・スヴォボダ (2010). 『電気回路入門（第8版）』 ジョン・ワイリー・アンド・サンズ. p.  661. ISBN 978-0-470-52157-1。
10. アラン・H・ロビンズ、ウィルヘルム・ミラー (2012). 『回路解析：理論と実践』（第5版）. Cengage Learning. 536ページ. ISBN 978-1-285-40192-8。
11. Won Y. Yang; Seung C. Lee (2008). MATLABとPSpiceによる回路システム. John Wiley & Sons. pp.  256– 261. ISBN 978-0-470-82240-1。
12. バジル・マホン (2017). 『オリバー・ヘヴィサイドの忘れられた天才』（第1版）. プロメテウス・ブックス・ラーニング. p. 230. ISBN 978-1-63388-331-4。
13. ニルソン, ジェームズ・ウィリアム; リーデル, スーザン・A. (2008).電気回路（第8版）. プレンティス・ホール. p. 338. ISBN 978-0-13-198925-2。第9章、338ページ
14. ローリンズ、ジョン・C. (2000).基本交流回路（第2版）. ニューネス. pp.  427– 452. ISBN 9780750671736。
15. Singh, Ravish R (2009). 「セクション4.5: 交番量の位相器表現」.電気回路網. Mcgraw Hill Higher Education. p. 4.13. ISBN 978-0070260962。
16. クレイトン、ポール (2008).電磁両立性入門. Wiley. p. 861. ISBN 978-81-265-2875-2。
17. de Oliveira, HMとNunes, FD「アナロジカル振幅変調における位相器経路について」国際工学科学研究ジャーナル（IJRES）第2巻、N.1、2014年1月、pp.11-18、ISSN 2320-9364

さらに読む

• ダグラス・C・ジャンコリ（1989年）『科学者とエンジニアのための物理学』プレンティス・ホール出版、ISBN 0-13-666322-2。
• リチャード・C・ドーフ; ロナルド・J・タラリダ (1993年7月15日).電気工学公式ポケットブック(第1版). ボカラトン, フロリダ州: CRC Press. pp.  152– 155. ISBN 0849344735。

外部リンク

• フェイザーファクトリー
• 位相器の視覚的表現
• 極座標表記と直交座標表記
• 通信における位相器