光子
光子
構成素粒子
統計ボーズ・アインシュタイン統計
家族ゲージボソン
相互作用電磁力、重力
シンボルγ
理論化されたアルバート・アインシュタイン（1905年）「光子」という名前は、一般的にギルバート・N・ルイス（1926年）に由来すると考えられている。
質量0（理論値）<1 × 10 −18  eV/ c 2（実験限界）[ 1 ]
平均寿命安定[ 1 ]
電荷0 <1 × 10 −35  e（実験限界）‍ [1 ]
カラーチャージいいえ
スピン1  ħ
スピン状態+1  ħ、 −1  ħ
パリティ−1 [ 1 ]
Cパリティ−1 [ 1 ]
要約I ( J P C ) = 0, 1 (1 −− ) [ 1 ]

光子（古代ギリシャ語のφῶς , φωτός ( phôs, phōtós ) 「光」に由来）は、光や電波などの電磁波を含む電磁場の量子であり、電磁力の力の媒介となる素粒子です。光子は質量がなく、真空中で測定される光速でしか移動できません。光子はボソン粒子のクラスに属します。  

他の素粒子と同様に、光子は量子力学によって最もよく説明され、波動と粒子の両方の特性を備えた挙動を示す波動粒子二重性を示す。[ 2 ]現代の光子の概念は、マックス・プランクの研究を基にしたアルバート・アインシュタインの研究によって、20世紀の最初の20年間に始まった。プランクは、物質と電磁放射が互いに熱平衡状態にある仕組みを説明しようとしていたが、物質の中に蓄えられたエネルギーは整数個の離散的で等しい大きさの部分で構成されていると見なすべきであると提唱した。光電効果を説明するために、アインシュタインは光自体が離散的なエネルギー単位で構成されているという考えを導入した。1926年、ギルバート・N・ルイスはこれらのエネルギー単位を表す用語を光子という。 [ 3 ] [ 4 ] [ 5 ]その後、他の多くの実験によってアインシュタインのアプローチが検証された。[ 6 ] [ 7 ] [ 8 ]

素粒子物理学の標準モデルでは、光子やその他の素粒子は、時空のあらゆる点で特定の対称性を持つ物理法則の必然的な結果として説明されます。電荷、質量、スピンなどの粒子の固有の特性は、ゲージ対称性によって決定されます。光子の概念は、レーザー、ボーズ・アインシュタイン凝縮、場の量子論、量子力学の確率的解釈など、実験物理学と理論物理学の重要な進歩をもたらしました。光化学、高解像度顕微鏡、分子間距離の測定に応用されています。さらに、光子は量子コンピュータの要素として研究されており、量子暗号などの光イメージングや光通信への応用についても研究されています。

物理的特性

光子は電荷を持たず[ 9 ] [ 10 ] 、一般的に静止質量はゼロであると考えられており[ 11 ]、安定粒子です。光子の質量の実験的上限[ 12 ] [ 13 ]は非常に小さく、10の-53乗グラム程度です。そのため、その寿命は10の18乗年以上になります[ 14 ]。比較のために、宇宙の年齢は約1.38 × 10の10乗年です。

真空中では、光子は2つの偏光状態をとることができる。[ 15 ]光子は電磁気学におけるゲージボソンであるため、[ 16 ] : 29–30 光子の他のすべての量子数（レプトン数、重粒子数、フレーバー量子数など）はゼロである。[ 17 ]また、光子はボーズ・アインシュタイン統計に従うが、フェルミ・ディラック統計には従わない。つまり、光子はパウリの排他原理に従わず、[ 18 ] : 1221 複数の光子が同じ束縛量子状態を占めることができる。

光子は、電荷が加速されシンクロトロン放射を放出するときに放出されます。分子、原子、または原子核が低いエネルギー準位に遷移する際に放出される光子は、電波からガンマ線に至るまでの特性エネルギーを持ちます。また、粒子とその反粒子が消滅する際にも光子が放出されます（例えば、電子-陽電子消滅）。[ 18 ]：572、1114、1172

エネルギーと勢い

円錐は光子の波数4ベクトルの取り得る値を示しています。「時間」軸は角周波数（rad⋅s −1）、「空間」軸は角波数（rad⋅m −1）を表します。緑と藍は左偏光と右偏光を表します。

量子力学モデルでは、電磁波は光子のエネルギーを周波数に比例して伝達する（）[ 19 ]：325 ν{\displaystyle \nu}

E＝hν{\displaystyle E=h\nu }

ここで、hはプランク定数（基礎物理定数）です。エネルギーは角周波数（）または 波長（λ）で表すことができます。 ω{\displaystyle \omega }

E＝ℏω＝hcλ{\displaystyle E=\hbar \,\omega ={\frac {\,h\,c\,}{\lambda }}}

ここでħ≡⁠​h/ 2π​⁠は換算プランク定数と呼ばれ、 cは光速です。

光子の 運動量

p＝ℏけ 、{\displaystyle {\boldsymbol {p}}=\hbar {\boldsymbol {k}}~,}

ここでkは波数ベクトルであり、

は光子の伝播方向を指している ので、その運動量の大きさはp{\displaystyle {\boldsymbol {p}}}

p≡|p|＝ℏけ＝hνc＝hλ 。{\displaystyle p\equiv \left|{\boldsymbol {p}}\right|=\hbar k={\frac {\,h\nu \,}{c}}={\frac {\,h\,}{\lambda }}~.}

光子のエネルギーはE = pcと表すことができます。ここでpは運動量ベクトルpの大きさです。これは特殊相対論のエネルギーと運動量の関係と一致しています。

E2＝p2c2+メートル2c4{\displaystyle E^{2}=p^{2}c^{2}+m^{2}c^{4}}

m = 0のとき。[ 21 ]

偏極とスピン角運動量

光子はスピン角運動量も運び、これは光子の偏光と関連しています。（光線は光の軌道角運動量として説明される特性も示します）。

光子の角運動量は、+ħまたは-ħの2つの値を取ります。これらの2つの値は、円偏光の2つの純粋な状態に対応します。光線中の光子の集合は、これらの2つの値が混在することがあります。直線偏光の光ビームは、あたかも2つの角運動量が同数で構成されているかのように振舞います。[ 19 ] : 325

光のスピン角運動量は周波数に依存せず、1931年にCVラマンとスリ・バガヴァンタムによって実験的に検証された。 [ 22 ]

反粒子消滅

粒子と反粒子の衝突により光子が生成されることがある。自由空間では少なくとも2つの光子が生成されなければならない。なぜなら、運動量系の中心では衝突する反粒子は正味の運動量を持たないのに対し、単一の光子は常に運動量を持つからである（運動量は光子の周波数または波長によって決まり、ゼロにはならない）。したがって、運動量保存則（あるいは並進不変性）は、正味の運動量がゼロの光子が少なくとも2つ生成されることを要求する。[ 23 ]：64–65 2つの光子のエネルギー、あるいは周波数は、四元運動量保存則から決定できる。

別の見方をすれば、光子はそれ自身の反粒子とみなすことができる（したがって、「反光子」とは、単に反対の運動量、等しい偏光、そして180°位相がずれた通常の光子である）。その逆の過程である対生成は、ガンマ線などの高エネルギー光子が物質を通過する際にエネルギーを失う主要なメカニズムである。[ 24 ]この過程は、原子核の電場において許容される「1光子への消滅」の逆である。

電磁放射のエネルギーと運動量に関する古典的な公式は、光子事象を用いて再表現することができる。例えば、物体に対する電磁放射の圧力は、単位時間と単位面積あたりの光子運動量の物体への移動から生じる。圧力は単位面積あたりの力であり、力は単位時間あたりの運動量の変化だからである。[ 25 ]

光子の質量に関する実験的検証

現在広く受け入れられている物理理論は、光子が厳密に質量ゼロであると示唆、あるいは仮定している。もし光子が純粋に質量ゼロでなければ、その速度は周波数によって変化し、低エネルギー（より赤い）光子は高エネルギー光子よりもわずかに遅く移動する。相対性理論はこれに影響されない。つまり、いわゆる光速cは、光が実際に移動する速度ではなく、あらゆる物体が理論的に時空内で到達できる速度の上限を示す自然定数となる。 [ 26 ]したがって、それは依然として時空のさざ波（重力波と重力子）の速度ではあるが、光子の速度ではない。

もし光子の質量がゼロでなければ、他の効果も存在する。クーロンの法則は修正され、電磁場は余分な物理的自由度を持つことになる。これらの効果は、光速の周波数依存性よりも光子質量のより高感度な実験的プローブをもたらす。クーロンの法則が厳密には有効でないとすれば、外部電場にさらされた中空導体内に電場が存在する可能性がある。これはクーロンの法則を精密に検証する手段となる。[ 27 ]このような実験の無結果から、 m ≲の限界が設定された。10 −14  eV/ c 2 . [ 28 ]

光の質量のより明確な上限は、銀河ベクトルポテンシャルによって引き起こされる効果を検出するために設計された実験によって得られました。銀河磁場は広大な長さスケールで存在するため、銀河ベクトルポテンシャルは大きくなりますが、光子が質量を持たない場合、観測できるのは磁場のみとなります。光子が質量を持つ場合、質量項は1/2⁠ m 2 A μ A μは銀河プラズマに影響を与える。そのような効果が見られないという事実は、光子質量の上限がm <であることを示唆している。3 × 10 −27  eV/ c 2 である。 [ 29 ]銀河ベクトルポテンシャルは、磁化されたリングに作用するトルクを測定することによって直接調べることもできる。 [ 30 ]このような方法は、1.07 × 10 −27  eV/ c 2 ( 粒子データグループによって与えられた10 −36 Da）である。[ 31 ]

銀河ベクトルポテンシャルによる効果が観測されないことから生じるこれらの鋭い限界は、モデルに依存することが示されている。[ 32 ]光子の質量がヒッグス機構によって生成される場合、 m ≲の上限はクーロンの法則のテストから得られた 10 −14  eV/ c 2 は有効です。

歴史的発展

トーマス・ヤングによる水面の波の観察に基づいた干渉のスケッチ。[ 33 ]ヤングは、光で観察された同様の効果がニュートンの光の粒子理論ではなく波動モデルを支持すると推論した。[ 18 ] : 964

18世紀までのほとんどの理論では、光は粒子で構成されていると考えられていました。粒子モデルでは光の屈折、回折、複屈折を容易に説明できないため、ルネ・デカルト（1637年）[ 34 ] 、ロバート・フック（1665年）[ 35 ]、クリスティアーン・ホイヘンス（1678年）[ 36 ]によって光の波動理論が提唱されました。しかし、主にアイザック・ニュートンの影響により、粒子モデルは依然として主流でした。[ 37 ] 19世紀初頭、トーマス・ヤングとオーガスト・フレネルは光の干渉と回折を明確に示し、1850年までに波動モデルが一般的に受け入れられました。[ 38 ]ジェームズ・クラーク・マクスウェルが1865年に光は電磁波であると予測したこと[ 39 ] ― これは1888年にハインリヒ・ヘルツが電波を検出して実験的に確認された[ 40 ] ― は光の粒子モデルに最後の打撃を与えたように思われた。

1900年、マクスウェルの光の理論モデルは、振動する電場と磁場として完成されたように見えました。しかし、いくつかの観測結果は電磁放射のいかなる波動モデルでも説明できず、光エネルギーはE = hνで表される量子に包み込まれているという考えに至りました。その後の実験により、これらの光量子は運動量も持ち、粒子とみなせることが示されました。こうして光子の概念が生まれ、電場と磁場そのものへのより深い理解につながりました。

しかしながら、マクスウェル波動理論は光のすべての特性を説明しているわけではない。マクスウェル理論は光波のエネルギーはその強度のみに依存し、周波数には依存しないと予測している。しかしながら、いくつかの独立した種類の実験は、光が原子に与えるエネルギーは光の強度ではなく周波数のみに依存することを示している。例えば、ある化学反応はある閾値よりも高い周波数の光によってのみ引き起こされ、閾値よりも低い周波数の光は、どんなに強度が高くても反応を開始しない。同様に、十分に高い周波数の光を金属板に照射すると、電子は金属板から弾き出される（光電効果）。弾き出された電子のエネルギーは光の強度ではなく周波数のみに関係する。[ 41 ]

同時に、40年（1860年から1900年）にわたり様々な研究者によって行われた黒体放射の研究[ 42 ]は、マックス・プランクの仮説[ 43 ] [ 44 ]に結実しました。その仮説とは、周波数νの電磁放射を吸収または放射するあらゆる系のエネルギーは、エネルギー量子E = hνの整数倍であるというものです。アルバート・アインシュタイン[ 45 ] [ 46 ]が示したように、物質と電磁放射の間に観測される熱平衡を説明するには、何らかの形のエネルギー量子化を仮定する必要があります。この光電効果の説明により、アインシュタインは1921年のノーベル物理学賞を受賞しました。[ 47 ]

マクスウェルの光理論は、電磁放射のあらゆるエネルギーを許容するため、ほとんどの物理学者は当初、エネルギーの量子化は、放射を吸収または放射する物質に対する何らかの未知の制約から生じると仮定しました。1905年、アインシュタインは、エネルギーの量子化は電磁放射自体の特性であると初めて提唱しました。[ 45 ]アインシュタインは、マクスウェルの理論の妥当性を認めたものの、マクスウェル光波のエネルギーが、波自体は空間に連続的に広がっていても、互いに独立して動く点状の量子に局在していれば、多くの異常な実験を説明できると指摘しました。[ 45 ] 1909年[ 46 ]と1916年[ 48 ]に、アインシュタインは、黒体放射に関するプランクの法則が受け入れられる場合、エネルギー量子も運動量p = ⁠を運ばなければならないことを示しました。 h / λ ⁠、それらは本格的な粒子になります。

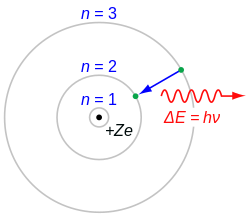
1923年まで、ほとんどの物理学者は光そのものが量子化されているという事実を受け入れることに消極的でした。代わりに、彼らは水素原子のボーア模型（ここに示す）のように、物質のみを量子化することで光子の振る舞いを説明しようとしました。これらの半古典的モデルは第一近似に過ぎませんでしたが、単純な系に対しては正確であり、量子力学へとつながりました。

ロバート・ミリカンの1923年のノーベル講演で述べられているように、アインシュタインが1905年に予測したエネルギー関係は1916年までに実験的に検証されたが、量子の局所概念は未解決のままであった。 [ 49 ] ほとんどの物理学者は、電磁放射自体が粒子状であり、したがって波動粒子二重性の例である可能性があると信じたがらなかった。[ 50 ] その後、1922年にアーサー・コンプトンの実験[ 51 ]により、光子は波数に比例した運動量を持っていることが示され（1922年）、現在ではコンプトン散乱と呼ばれているこの実験は、局所量子モデルを明確に支持するように見えた。少なくともミリカンにとっては、これで問題は解決した。[ 49 ]コンプトンは散乱に関する研究で1927年にノーベル賞を受賞した。

コンプトンの実験の後も、ニールス・ボーア、ヘンドリック・クレイマース、ジョン・スレーターは、光のマクスウェル連続電磁場モデル、いわゆるBKS理論を維持しようと最後の試みを行った。[ 52 ] BKS理論の重要な特徴は、エネルギー保存則と運動量保存則の扱い方である。BKS理論では、エネルギーと運動量は、物質と放射線の間の多くの相互作用において平均的にのみ保存される。しかし、改良されたコンプトン実験は、個々の相互作用において保存則が成り立つことを示した。[ 53 ]そのため、ボーアと彼の同僚たちは、彼らのモデルに「可能な限り名誉ある葬儀」を執り行った。[ 54 ]しかし、BKSモデルの失敗は、ヴェルナー・ハイゼンベルクの行列力学の発展に影響を与えた。[ 55 ]

1920年代後半には、マクスウェルの光の波動理論と、実験的に観測されたその粒子性をいかに統一するかが重要な問題となった。この問題の答えはアルバート・アインシュタインの生涯をかけて解明され[ 54 ] 、量子電磁力学とその後継である標準模型によって解明された。（後述の「量子場の理論」および「ゲージボソンとして」を参照。）

少数の物理学者は、電磁放射は量子化されていないが、物質は量子力学の法則に従うという半古典的モデルの開発に固執した[ 56 ]。1970年代までに、光子の存在を示す化学的および物理的な実験による証拠は圧倒的であったが、この証拠は光と物質の相互作用に依存しており、十分に完全な物質理論が原理的にその証拠を説明できるため、絶対的に決定的なものとは考えられなかった。

1970年代と1980年代には、光子相関実験によって量子光子効果が明確に実証された。これらの実験は、量子測定過程に起因する反相関を伴うため、いかなる古典的な光理論でも説明できない結果をもたらす。1974年、クラウザーが初めてこのような実験を行い、古典的なコーシー・シュワルツ不等式が破れることを報告した。1977年、キンブルらはビームスプリッターと相互作用する光子の類似した反集束効果を実証した。このアプローチは、グランジェ、ロジャー、アスペクト（1986年）による光子反相関実験で簡略化され、誤差源が排除された。[ 57 ]この研究は、ソーン、ニールら（2004年）でさらにレビューされ、簡略化されている。 [ 58 ]

命名法

光電効果：光量子（光子）によって引き起こされる金属板からの電子の放出

量子（単数形は量子、ラテン語で「どれだけの量」を意味する）という言葉は、1900年以前は粒子や、電気を含む様々な量の量を意味するために使われていました。1900年、ドイツの物理学者マックス・プランクは黒体放射を研究しており、特に短波長における実験観測は、エネルギーが「完全に定められた数の有限の等しい部分」で構成されているとすれば説明できると示唆しました。彼はこれを「エネルギー要素」と呼びました。[ 59 ] 1905年、アルベルト・アインシュタインは論文を発表し、黒体放射や光電効果を含む多くの光関連現象は、電磁波を空間的に局在した離散的なエネルギー量子で構成されているとモデル化することでよりよく説明できると提唱しました。[ 45 ]彼はこれを光量子（ドイツ語：ein Lichtquant）と呼びました。[ 60 ]

光子（photon）という名称は、光を意味するギリシャ語φῶς（音訳：phôs ）に由来する。この名称は1916年、アメリカの物理学者で心理学者のレナード・T・トロランドによって、網膜の照明の単位として、また物理学に採用される前のいくつかの文脈でも使用された。[ 5 ]光量子に対する光子という用語の使用は、ギルバート・N・ルイスによって普及した。彼は1926年12月18日付のネイチャー誌への手紙の中でこの用語を使用した。[ 61 ]光量子を実証する重要な実験を行ったアーサー・コンプトンは、1927年のソルベー会議の議事録の中で、ルイスが光子という名称を提案したことを引用している。アインシュタインはこの用語を結局使用しなかった。[ 5 ]

物理学では、光子は通常、記号γ（ギリシャ文字のガンマ）で表されます。この光子の記号は、おそらくガンマ線に由来しています。ガンマ線は1900年にポール・ヴィラードによって発見され、[ 62 ] [ 63 ] 、アーネスト・ラザフォードによって1903年に命名され、1914年にラザフォードとエドワード・アンドラーデによって電磁放射の一種であることが示されました。[ 64 ]化学と光工学では、光子は通常、光子エネルギーであるhνで表されます。hはプランク定数、ギリシャ文字のν（ニュー）は光子の周波数です。[ 65 ]

波動粒子二重性と不確定性原理

光子は量子力学の法則に従うため、その振る舞いには波動と粒子の両方の側面がある。光子が測定機器で検出されると、それは単一の粒子単位として記録される。しかし、光子が検出される確率は、波を記述する方程式によって計算される。この側面の組み合わせは、波動粒子二重性として知られている。たとえば、光子が検出される可能性のある場所の確率分布は、回折や干渉などの波動現象を明確に示す。二重スリットを通過する単一の光子は、スクリーン上のある点でエネルギーを受け取り、その確率分布は、マクスウェルの波動方程式によって決定される干渉パターンによって与えられる。[ 66 ]しかし、実験により、光子は電磁放射の短いパルスではないことが確認されている。光子のマクスウェル波は回折するが、光子エネルギーは伝播するときに拡散せず、ビームスプリッターに遭遇してもこのエネルギーは分割されない。[ 67 ]むしろ、受信した光子は、原子核（直径≈10-15m ）や点状電子など、その波長よりもはるかに小さい系を含む任意の小さな系によって全体として吸収または放出されるため、点状粒子のように振る舞います。

多くの入門書では、光子を非相対論的量子力学の数学的手法を用いて扱っているが、これはある意味で不自然な単純化である。なぜなら、光子は本質的に相対論的だからである。光子の静止質量はゼロであるため、光子に対して定義された波動関数は、非相対論的量子力学の波動関数に見られるすべての性質を持つことはできない。[ a ]これらの困難を回避するために、物理学者は後述する光子の第二量子化理論、すなわち量子電気力学を用いる。この理論では、光子は電磁モードの量子化された励起である。[ 72 ]

もう一つの難しさは、不確定性原理の適切な類似例を見つけることです。この概念は、電子と高エネルギー光子を用いた思考実験の分析においてハイゼンベルクが提唱したものとしばしば考えられています。しかし、ハイゼンベルクはこれらの測定における「不確定性」が何を意味するのか、正確な数学的定義を与えていません。位置・運動量の不確定性原理の正確な数学的記述は、ケナード、パウリ、ワイルによってなされました。[ 73 ] [ 74 ]不確定性原理は、実験者が粒子の位置と運動量のような「正準共役」な2つの量のうち、どちらか一方を測定するという選択肢を持つ状況に適用されます。不確定性原理によれば、粒子がどのように準備されたとしても、2つの代替測定の両方について正確な予測を行うことはできません。位置測定の結果がより確実であれば、運動量測定の結果はより確実ではなくなり、その逆も同様です。[ 75 ]コヒーレント状態は、量子力学が許す限り、全体的な不確定性を最小化します。[ 72 ]量子光学は電磁場のモードとしてコヒーレント状態を利用する。電磁波の振幅と位相の測定値の間には、位置と運動量の不確定性関係を彷彿とさせるトレードオフが存在する。[ 72 ]これは、電磁波中に存在する光子数の不確定性と、波の位相の不確定性として非公式に表現されることがある。しかし、位置や運動量とは異なり、位相はエルミート演算子で表すことができないため、これはケナード・パウリ・ワイル型の不確定性関係にはなり得ない。[ 76 ]Δ北{\displaystyle \Delta N}Δϕ{\displaystyle \Delta \phi }ϕ{\displaystyle \phi }

光子ガスのボーズ・アインシュタインモデル

1924年、サティエンドラ・ナート・ボースは、プランクの黒体放射の法則を、電磁気学を一切用いず、位相空間の粗視化計数法の修正によって導出した。[ 77 ]アインシュタインは、この修正は光子が厳密に同一であると仮定することと等価であり、それが「神秘的な非局所的相互作用」を意味することを示した。 [ 78 ] [ 79 ]これは現在では対称的な量子力学的状態の要件として理解されている。この研究はコヒーレント状態の概念とレーザーの開発につながった。同じ論文で、アインシュタインはボースの形式論を物質粒子（ボソン）に拡張し、それらが十分に低い温度で最低の量子状態に凝縮すると予測した。このボーズ・アインシュタイン凝縮は1995年に実験的に観測された。[ 80 ]その後、レネ・ハウは1999年[ 81 ]と2001年にこの現象を利用して光を遅くし、そして完全に止めることに成功した。[ 82 ]

これに関する現代の見解では、光子は整数スピンを持つため、ボソンである（半整数スピンを持つフェルミオンとは対照的である）。スピン統計定理によれば、すべてのボソンはボーズ＝アインシュタイン統計に従う（一方、すべてのフェルミオンはフェルミ＝ディラック統計に従う）。[ 83 ]

誘導放出と自然放出

誘導放出（光子が自らを「複製」する現象）は、アインシュタインの運動論的解析によって予言され、レーザーの開発につながりました。アインシュタインの導出は、光の量子論的扱いにおけるさらなる発展を促し、量子力学の統計的解釈へとつながりました。

1916年、アルバート・アインシュタインは、プランクの放射法則が光子と原子の半古典的な統計的処理から導かれることを示しました。これは、原子が光子を放出する速度と吸収する速度の間に関連があることを意味します。この条件は、原子による放射の放出と吸収の関数が互いに独立しており、熱平衡は放射と原子の相互作用によって達成されるという仮定から生じます。すべての部分が熱平衡状態にあり、電磁放射で満たされた空洞を考えてみましょう。原子は電磁放射を放出および吸収できます。熱平衡状態を保つには、周波数（光子の数密度に比例する）の光子のエネルギー密度が平均して時間的に一定である必要があります。したがって、特定の周波数の光子が放出される速度は、吸収される速度と等しくなければなりません。[ 84 ]ρ（ν）{\displaystyle \rho (\nu )}ν{\displaystyle \nu}

アインシュタインは、関係する様々な反応速度について単純な比例関係を仮定することから始めました。彼のモデルでは、系が特定の周波数の光子を吸収し、低エネルギーから高エネルギーへと遷移する速度は、エネルギーを持つ原子の数と、その周波数の周囲の光子の エネルギー密度に比例します。Rj私{\displaystyle R_{ji}}ν{\displaystyle \nu}Ej{\displaystyle E_{j}}E私{\displaystyle E_{i}}北j{\displaystyle N_{j}}Ej{\displaystyle E_{j}}ρ（ν）{\displaystyle \rho (\nu )}

Rj私＝北jBj私ρ（ν）{\displaystyle R_{ji}=N_{j}B_{ji}\rho (\nu )\!}

ここで、は吸収の速度定数である。逆の過程には、2つの可能性がある。光子の自然放出、または原子と通過する光子との相互作用によって開始される光子放出と、原子が低エネルギー状態に戻ることによるものである。アインシュタインのアプローチに従うと、高エネルギーから低エネルギーへの遷移を伴う周波数の光子放出の対応する速度は、 Bj私{\displaystyle B_{ji}}R私j{\displaystyle R_{ij}}ν{\displaystyle \nu}E私{\displaystyle E_{i}}Ej{\displaystyle E_{j}}

R私j＝北私あ私j+北私B私jρ（ν）{\displaystyle R_{ij}=N_{i}A_{ij}+N_{i}B_{ij}\rho (\nu )\!}

ここで、は自発的に光子を放出する速度定数であり、は周囲の光子に応答して放出される（誘導放出または刺激放出）速度定数である。熱力学的平衡において、状態と状態 の原子の数は平均して一定でなければならない。したがって、速度と速度は等しくなければならない。また、ボルツマン統計の導出に類似した議論により、と の比はとなる。ここで、と はそれぞれ状態との縮退度、それらのエネルギー、ボルツマン定数、および系の温度である。このことから、次の式が容易に導かれる。 あ私j{\displaystyle A_{ij}}B私j{\displaystyle B_{ij}}私{\displaystyle i}j{\displaystyle j}Rj私{\displaystyle R_{ji}}R私j{\displaystyle R_{ij}}北私{\displaystyle N_{i}}北j{\displaystyle N_{j}}グラム私/グラムj経験⁡（Ej−E私）/（けT）、{\displaystyle g_{i}/g_{j}\exp {(E_{j}-E_{i})/(kT)},}グラム私{\displaystyle g_{i}}グラムj{\displaystyle g_{j}}私{\displaystyle i}j{\displaystyle j}E私{\displaystyle E_{i}}Ej{\displaystyle E_{j}}け{\displaystyle k}T{\displaystyle T}

グラム私B私j＝グラムjBj私{\displaystyle g_{i}B_{ij}=g_{j}B_{ji}}

そして

あ私j＝8πhν3c3B私j。{\displaystyle A_{ij}={\frac {8\pi h\nu ^{3}}{c^{3}}}B_{ij}.}

とは総じてアインシュタイン係数として知られています。[ 85 ]あ私j{\displaystyle A_{ij}}B私j{\displaystyle B_{ij}}

アインシュタインは自身の反応速度方程式を完全には正当化できなかったが、係数を計算することは可能であり、物理学者たちは「量子仮説に適応するように修正された力学と電気力学」を手に入れたと主張した。[ 86 ]それから間もなく、1926年にポール・ディラックは半古典的なアプローチを用いて反応速度定数を導き出し、 [ 87 ]そして1927年には量子論の枠組みの中で第一原理からすべての反応速度定数を導くことに成功した。[ 88 ] [ 89 ]ディラックの研究は量子電気力学、すなわち電磁場自体の量子化の基礎となった。ディラックのアプローチは第二量子化または量子場理論とも呼ばれる。[ 90 ] [ 91 ] [ 92 ]初期の量子力学的扱いでは物質粒子のみを量子力学的に扱い、電磁場は扱っていなかった。 あ私j{\displaystyle A_{ij}}Bj私{\displaystyle B_{ji}}B私j{\displaystyle B_{ij}}B私j{\displaystyle B_{ij}}

アインシュタインは、自らの理論が不完全であるように思われる点に悩まされていました。なぜなら、それは自発的に放出された光子の方向を決定しないからです。光粒子の運動の確率的性質は、ニュートンが複屈折、そしてより一般的には界面における光線の透過光線と反射光線への分岐を扱う際に初めて考慮されました。ニュートンは、光粒子に隠れた変数が、単一の光子がどちらの経路を取るかを決定すると仮説を立てました。 [ 37 ]同様に、アインシュタインは偶然に任せないより完全な理論を望み、量子力学から離れ始めました[ 54 ] 。皮肉なことに、マックス・ボルンによる波動関数の確率的解釈[ 93 ] [ 94 ]は、より完全な理論を模索したアインシュタインの後の研究に触発されたものでした[ 95 ] 。

量子場理論

電磁場の量子化

異なる電磁モード（ここに示したものなど）は、独立した単純な調和振動子として扱うことができます。光子は、その電磁モードにおいてエネルギー単位E  =  hνに対応します。

1910年、ピーター・デバイは比較的単純な仮定からプランクの黒体放射の法則を導出した。 [ 96 ]彼は空洞内の電磁場をフーリエモードに分解し、どのモードのエネルギーも の整数倍であると仮定した。ここでは電磁モードの周波数である。プランクの黒体放射の法則は幾何学的和として直ちに導かれる。しかし、デバイのアプローチは黒体放射のエネルギー変動の正しい式を与えることができず、これは1909年にアインシュタインによって導出された。[ 46 ]hν{\displaystyle h\nu }ν{\displaystyle \nu}

1925 年、ボルン、ハイゼンベルク、ジョーダンはデバイの概念を重要な方法で再解釈しました。[ 97 ]古典的に示すように、電磁場のフーリエモード(波数ベクトルkと偏光状態でインデックス付けされた電磁平面波の完全なセット) は、結合していない単純な調和振動子のセット と等価です。量子力学的に扱うと、このような振動子のエネルギーレベルは であることがわかっており、ここでは振動子周波数です。重要な新しいステップは、エネルギー を持つ電磁モードを、各エネルギー を持つ光子の状態として特定することでした。このアプローチにより、正しいエネルギーゆらぎの式が得られます。 E＝nhν{\displaystyle E=nh\nu }ν{\displaystyle \nu}E＝nhν{\displaystyle E=nh\nu }n{\displaystyle n}hν{\displaystyle h\nu }

仮想光子の交換によって相互作用する2つの電子のファインマン図

ディラックはこれをさらに一歩進めた。[ 88 ] [ 89 ]彼は電荷と電磁場との相互作用を、光子の状態の遷移を誘発し、モード内の光子の数を変えながら、全体としてエネルギーと運動量を保存する小さな摂動として扱った。ディラックはアインシュタインの係数を第一原理から導き出し、光子のボーズ・アインシュタイン統計は電磁場を正しく量子化することの自然な帰結であることを示した（ボーズの推論は逆方向に進み、彼はB-E統計を仮定してプランクの黒体放射の法則を導き出した）。ディラックの時代には、光子を含むすべてのボソンがボーズ・アインシュタイン統計に従わなければならないことはまだ知られていなかった。 あ私j{\displaystyle A_{ij}}B私j{\displaystyle B_{ij}}

ディラックの2次摂動論は、電磁場の過渡的中間状態である仮想光子を扱うことができる。静的電気・磁気相互作用は、このような仮想光子によって媒介される。このような量子場理論では、観測可能な事象の確率振幅は、非物理的なものも含め、すべての可能な中間ステップを合計することによって計算される。したがって、仮想光子はを満たすように制約されず、追加の偏光状態を持つ可能性がある。使用されるゲージに応じて、仮想光子は、実在の光子の2つの状態の代わりに、3つまたは4つの偏光状態を持つことができる。これらの過渡的仮想光子は決して観測されないが、観測可能な事象の確率に測定可能なほど寄与する。[ 98 ]E＝pc{\displaystyle E=pc}

2次および高次の摂動計算では、和に無限の寄与を与える可能性がある。このような非物理的な結果は、繰り込みの手法を用いて補正される。[ 99 ]

他の仮想粒子も加算に寄与する可能性がある。例えば、2つの光子は仮想電子-陽電子対を介して間接的に相互作用する可能性がある。[ 100 ]このような光子-光子散乱（ 2光子物理学を参照）は、電子-光子散乱と同様に、計画されている粒子加速器である国際線形衝突型加速器（ILC）の動作モードの1つとなることが意図されている。[ 101 ]

現代物理学の記法では、電磁場の量子状態は、各電磁モードの状態の テンソル積であるフォック状態として表される。

|nけ0⟩⊗|nけ1⟩⊗⋯⊗|nけn⟩…{\displaystyle |n_{k_{0}}\rangle \otimes |n_{k_{1}}\rangle \otimes \dots \otimes |n_{k_{n}}\rangle \dots }

ここで、 は光子がモード にある状態を表します。この表記法では、モード における新しい光子の生成（例えば、原子遷移から放出される光子）は と書きます。この表記法は、上述のボルン、ハイゼンベルク、ジョーダンの概念を表現しているだけで、物理的な意味合いを付け加えるものではありません。 |nけ私⟩{\displaystyle |n_{k_{i}}\rangle }nけ私{\displaystyle \,n_{k_{i}}}け私{\displaystyle k_{i}}け私{\displaystyle k_{i}}|nけ私⟩→|nけ私+1⟩{\displaystyle |n_{k_{i}}\rangle \rightarrow |n_{k_{i}}+1\rangle }

ゲージボソンとして

電磁場はゲージ場、すなわち、時空内のすべての位置でゲージ対称性が独立に成立することを要求する場として理解することができる。[ 102 ]電磁場の場合、このゲージ対称性は絶対値1の複素数のアーベルU(1)対称性であり、観測可能量やエネルギーやラグランジアンなどの実数値関数に影響を与えずに複素場の位相を変化させる能力を反映している。

アーベルゲージ場の量子は、対称性が破れない限り、質量がなく荷電のないボソンでなければならない。したがって、光子は質量がなく、電荷がゼロで整数のスピンを持つと予測される。電磁相互作用の特定の形式は、光子がスピン±1を持つ必要があることを指定する。したがって、そのヘリシティはでなければならない。これらの2つのスピン成分は、古典的な右巻き円偏光と左巻き円偏光の概念に対応する。しかし、量子電磁力学の過渡的仮想光子は、非物理的な偏光状態をとることもある。[ 102 ]±ℏ{\displaystyle \pm \hbar }

物理学の一般的な標準モデルでは、光子は電弱相互作用における4つのゲージボソンの1つです。他の3つはW +、W −、Z 0で示され、弱い相互作用を担っています。光子とは異なり、これらのゲージボソンは、 SU(2)ゲージ対称性を破るメカニズムにより質量を持ちます。電弱相互作用における光子とWおよびZゲージボソンの統一は、シェルドン・グラショー、アブドゥス・サラム、スティーブン・ワインバーグによって達成され、 3人は1979年のノーベル物理学賞を受賞しました。 [ 103 ] [ 104 ] [ 105 ]物理学者は、これら4つのゲージボソンを量子色力学の8つのグルーオンゲージボソンに結び付ける大統一理論を仮説し続けています。しかし、陽子崩壊など、これらの理論の重要な予測は実験的には観測されていません。[ 106 ]

ハドロンの性質

高エネルギー光子とハドロンとの相互作用の測定により、相互作用は、単なる光子とハドロンの電荷との相互作用から予想されるよりもはるかに強力であることが示されています。さらに、陽子と中性子の電荷構造が大幅に異なるという事実にもかかわらず、高エネルギー光子と陽子の相互作用は、光子と中性子の相互作用に似ています[ 107 ] 。この効果を説明するために、ベクトル中間子優位性(VMD) と呼ばれる理論が開発されました。VMD によると、光子は、電荷とのみ相互作用する純粋な電磁光子と、残留核力を媒介するベクトル中間子の重ね合わせです[ 108 ]。しかし、非常に短い距離で実験的に調査すると、光子の固有構造は、 QCDの漸近自由度に従って準自由な、クォークとグルーオンの電荷中性フラックスを要素として持っているように見えます。このフラックスは光子構造関数によって記述される。[ 109 ] [ 110 ] Nisius（2000）によるレビューでは、データと理論的予測の包括的な比較が提示された。[ 111 ]

システムの質量への寄与

光子を放出する系のエネルギーは、放出系の静止系で測定された光子のエネルギーだけ減少し、その結果、質量が だけ減少する可能性がある。同様に、光子を吸収する系の質量は、対応する量だけ増加する。応用として、光子が関与する核反応のエネルギーバランスは、通常、関与する原子核の質量と、ガンマ光子（および原子核の反跳エネルギーなど、その他の関連するエネルギー）の形で表される。[ 112 ]E{\displaystyle E}E/c2{\displaystyle {E}/{c^{2}}}E/c2{\displaystyle {E}/{c^{2}}}

この概念は、量子電磁力学（QED、上記参照）の重要な予測に応用されている。この理論では、電子（あるいはより一般的にはレプトン）の質量は、再正規化と呼ばれる手法を用いて仮想光子の質量寄与を組み込むことで修正される。このような「放射補正」は、レプトンの磁気双極子モーメント、ラムシフト、そしてミューオニウムやポジトロニウムなどの束縛レプトン対の超微細構造など、QEDの多くの予測に貢献している。[ 113 ]

一般相対性理論によれば、光子は応力エネルギーテンソルに寄与するため、他の物体に重力を及ぼす。逆に、光子自身も重力の影響を受ける。通常は直線的な軌道が、重力レンズ効果のように歪んだ時空によって曲げられたり、パウンド・レプカ実験のように、より高い重力ポテンシャルに移動することで周波数が低下したりする。しかし、これらの効果は光子に特有のものではなく、古典的な電磁波にも全く同じ効果が予測される。[ 114 ]

物質的に

透明な物質を通過する光は、真空中の光速cよりも遅い速度で進みます。速度が低下する係数は、物質の屈折率と呼ばれます。古典的な波の見方では、光が物質に電気分極を誘導し、分極した物質が新しい光を放射し、その新しい光が元の光波と干渉して遅延波を形成することで、光の減速を説明できます。粒子の見方では、光の減速は、光子と物質の量子励起が混ざり合って、ポラリトンと呼ばれる準粒子が生成されることによって説明できます。ポラリトンは有効質量がゼロではないため、cで移動することはできません。異なる周波数の光は、異なる速度で物質を通過する場合があります。これは分散と呼ばれます（散乱と混同しないでください）。場合によっては、物質中の光速度が極端に遅くなることがあります。光子と他の準粒子の相互作用の影響は、ラマン散乱やブリルアン散乱で直接観測できます。[ 115 ]

光子は物質によって散乱されることがあります。例えば、太陽の中心核を離れた後、光子は太陽放射層で何度も散乱するため、放射エネルギーが対流層に到達するまでに約100万年かかります。[ 116 ]しかし、太陽の光球から放出された光子は地球に到達するまでにわずか8.3分しかかかりません。[ 117 ]

光子は原子核、原子、分子にも吸収され、エネルギー準位間の遷移を引き起こす。典型的な例は、視覚を司るレチナール（C 20 H 28 O）の分子遷移であり、これは1958年にノーベル賞受賞生化学者ジョージ・ウォルドとその同僚によって発見された。この吸収はシス-トランス異性化を引き起こし、これが他の遷移と相まって神経インパルスに変換される。光子の吸収は塩素の光解離のように化学結合を切断することさえあり、これは光化学の主題である。[ 118 ] [ 119 ]

技術的応用

光子は技術において多くの応用例を持っています。これらの例は、古典的な光理論の下で動作するレンズなどの一般的な光学デバイスではなく、光子そのものの応用例を説明するために選ばれました。レーザーは重要な応用例であり、誘導放出の項で既に説明されています。

個々の光子はいくつかの方法で検出できます。古典的な光電子増倍管は光電効果を利用しています。十分なエネルギーを持つ光子が金属板に衝突すると電子が弾き出され、電子の雪崩が絶えず増幅されます。半導体電荷結合素子チップも同様の効果を利用しています。入射光子は微小なコンデンサに電荷を発生させ、これを検出します。ガイガーカウンターなどの他の検出器は、光子が装置内のガス分子を電離させ、ガスの導電率に検出可能な変化を引き起こす能力を利用しています。 [ 120 ]

プランクのエネルギー公式は、エンジニアや化学者によって設計において頻繁に用いられ、光子の吸収によるエネルギー変化の計算と、与えられた光子放出から放出される光の周波数の決定に用いられます。例えば、ガス放電ランプの発光スペクトルは、電子エネルギー準位の異なるガス（の混合物）を充填することで変化させることができます。[ 121 ]E＝hν{\displaystyle E=h\nu }

特定の条件下では、個々では不十分な「2つの」光子によってエネルギー遷移が励起されることがあります。これにより、試料は異なる色の2つのビームが大きく重なり合うスペクトルのみでエネルギーを吸収するため、より高解像度の顕微鏡観察が可能になります。このスペクトルは、単一のビームによる励起体積よりもはるかに小さく抑えることができます（2光子励起顕微鏡法を参照）。さらに、これらの光子はエネルギーが低いため、試料へのダメージも少なくなります。[ 122 ]

場合によっては、2つのエネルギー遷移が結合し、一方の系が光子を吸収すると、近くの別の系がそのエネルギーを「奪い」、異なる周波数の光子を再放出することがあります。これは、分子生物学において適切なタンパク質の相互作用を研究するために使用される手法である蛍光共鳴エネルギー移動の基礎です。[ 123 ]

ハードウェア乱数生成器には、単一光子の検出を利用するものがいくつかある。例えば、生成する乱数列の各ビットに対して、光子がビームスプリッターに送られる。この場合、等確率で2つの結果が考えられる。実際の結果は、列の次のビットが0か1かを決定するために使用される。[ 124 ] [ 125 ]

量子光学と計算

量子光学の分野では、光子の応用に関する研究が盛んに行われてきました。光子は超高速量子コンピュータの要素として適していると考えられており、光子の量子もつれが研究の焦点となっています。非線形光学過程もまた活発な研究分野であり、二光子吸収、自己位相変調、変調不安定性、光パラメトリック発振器などが取り上げられています。しかし、このような過程は一般に光子そのものの存在を前提とする必要はなく、原子を非線形発振器として扱うことでモデル化できる場合が多いです。自発的なパラメトリックダウンコンバージョンという非線形過程は、単一光子状態の生成によく用いられます。最後に、光子は光通信、特に量子暗号において不可欠な要素となっています。[ 126 ]

二光子物理学は、稀な光子間の相互作用を研究する。2018年、マサチューセッツ工科大学の研究者らは、ポラリトンが関与している可能性のある束縛光子三重項を発見したと発表した。[ 127 ] [ 128 ]

参照

注記

  1. ^この問題は、セオドア・ダデル・ニュートンとユージン・ウィグナーによって初めて定式化された。 [ 68 ] [ 69 ] [ 70 ]これらの課題は、特殊相対論における時空の対称性を記述するローレンツ群の根本的な性質に起因している。ガリレイ変換の生成元とは異なり、ローレンツブーストの生成元は可換ではないため、相対論的粒子の位置のすべての座標に同時に低い不確定性を割り当てることは困難となる。 [ 71 ]

参考文献

  1. ^ a b c d e f Amsler, C.; et al. ( Particle Data Group ) (2008). 「Review of Particle Physics: Gauge and Higgs bosons」(PDF) . Physics Letters B. 667 ( 1): 1. Bibcode : 2008PhLB..667....1A . doi : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . S2CID  227119789. 2018年12月25日時点のオリジナルよりアーカイブ。2010年4月9日閲覧。
  2. ^ Joos, George (1951). 『理論物理学』 ロンドンおよびグラスゴー: Blackie and Son Limited. p. 679.
  3. ^ 「1926年12月18日：ギルバート・ルイスがネイチャー誌への手紙の中で「光子」という言葉を考案」 www.aps.org 。 2019年5月2日時点のオリジナルよりアーカイブ。 2019年3月9日閲覧。
  4. ^ 「ギルバート・N・ルイス」。原子力遺産財団。2015年4月16日時点のオリジナルよりアーカイブ。 2019年3月9日閲覧。
  5. ^ a b c Kragh, Helge (2014). 「光子：古い名前に新たな光を」. arXiv : 1401.0293 [ physics.hist-ph ].
  6. ^コンプトン、アーサー・H. (1965) [1927年12月12日]. 「光学の一分野としてのX線」(PDF) . 『ノーベル賞受賞記念講演 物理学 1922–1941』より. アムステルダム: エルゼビア出版社. 2024年5月12日時点のオリジナルよりアーカイブ(PDF) . 2019年1月3日閲覧。
  7. ^ Kimble, HJ; Dagenais, M.; Mandel, L. (1977). 「共鳴蛍光における光子アンチバンチング」(PDF) . Physical Review Letters . 39 (11): 691– 695. Bibcode : 1977PhRvL..39..691K . doi : 10.1103/PhysRevLett.39.691 . 2020年11月25日時点のオリジナルよりアーカイブ(PDF) . 2019年1月3日閲覧。
  8. ^ Grangier, P.; Roger, G.; Aspect, A. (1986). 「ビームスプリッターにおける光子反相関効果の実験的証拠：単一光子干渉の新たな視点」. Europhysics Letters . 1 (4): 173– 179. Bibcode : 1986EL......1..173G . CiteSeerX 10.1.1.178.4356 . doi : 10.1209/0295-5075/1/4/004 . S2CID 250837011 .  
  9. ^ Frisch, David H. ; Thorndike, Alan M. (1964). 『素粒子』 プリンストン、ニュージャージー州: David Van Nostrand . p. 22.
  10. ^ Kobychev, VV; Popov, SB (2005). 「銀河系外源の観測による光子電荷の制約」.天文学レターズ. 31 (3): 147– 151. arXiv : hep-ph/0411398 . Bibcode : 2005AstL...31..147K . doi : 10.1134/1.1883345 . S2CID 119409823 . 
  11. ^ Baez, John . 「光子の質量はいくらか？」（個人学術サイト）.カリフォルニア大学リバーサイド校. 2014年5月31日時点のオリジナルよりアーカイブ。 2009年1月13日閲覧。
  12. ^ Tu, Liang-Cheng; Luo, Jun; Gillies, George T (2005-01-01). 「光子の質量」 .物理学の進歩に関する報告. 68 (1): 77– 130. Bibcode : 2005RPPh...68...77T . doi : 10.1088/0034-4885/68/1/R02 . ISSN 0034-4885 . 
  13. ^ Goldhaber, Alfred Scharff; Nieto, Michael Martin (2010-03-23). 「光子と重力子の質量限界」 . Reviews of Modern Physics . 82 (1): 939– 979. arXiv : 0809.1003 . Bibcode : 2010RvMP...82..939G . doi : 10.1103/RevModPhys.82.939 . ISSN 0034-6861 . 2024年5月13日時点のオリジナルよりアーカイブ。 2024年2月1日閲覧。 
  14. ^ Heeck, Julian (2013-07-11). 「光子はどれほど安定しているのか？」 . Physical Review Letters . 111 (2) 021801. arXiv : 1304.2821 . Bibcode : 2013PhRvL.111b1801H . doi : 10.1103/PhysRevLett.111.021801 . ISSN 0031-9007 . PMID 23889385. 2024年5月13日時点のオリジナルよりアーカイブ。2024年2月1日閲覧。  
  15. ^シュワルツ、マシュー・D. (2014). 『量子場の理論と標準模型』ケンブリッジ大学出版局. p. 66. ISBN 978-1-107-03473-0。
  16. ^「ゲージボソンとしての役割と分極」 Aitchison, IJR; Hey, AJG (1993). Gauge Theories in Particle Physics . IOP Publishing . ISBN §5.1 978-0-85274-328-7. 2023年1月17日時点のオリジナルよりアーカイブ。2016年10月6日閲覧。
  17. ^ Amsler, C.; et al. (2008). "Review of Particle Physics" (PDF) . Physics Letters B. 667 ( 1– 5 ): 31. Bibcode : 2008PhLB..667....1A . doi : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . PMID 10020536. S2CID 227119789. 2020年6月1日時点のオリジナルよりアーカイブ(PDF) . 2017年10月26日閲覧.  
  18. ^ a b cハリデー、デイビッド、レスニック、ロバート、ウォーカー、ジャール (2005). 『物理学の基礎』（第7版）. ジョン・ワイリー・アンド・サンズ社. ISBN 978-0-471-23231-5。
  19. ^ a bヘクト、ユージーン (1998). Optics (第3版). Reading, Massachusetts; Harlow: Addison-Wesley. ISBN 978-0-201-83887-9。
  20. ^ Soper, Davison E. 「電磁放射は光子でできている」オレゴン大学理論科学研究所. 2023年4月8日時点のオリジナルよりアーカイブ。 2024年3月21日閲覧。
  21. ^ Alonso & Finn 1968、セクション1.6を参照
  22. ^ Raman, CV ; Bhagavantam, S. (1931). 「光子のスピンの実験的証明」(PDF) . Indian Journal of Physics . 6 (3244): 353. Bibcode : 1932Natur.129...22R . doi : 10.1038/129022a0 . hdl : 10821/664 . S2CID 4064852. 2016年6月3日時点のオリジナル(PDF)からのアーカイブ。 2008年12月28日閲覧。 
  23. ^グリフィス、デイビッド・J. (2008). 『素粒子入門（改訂第2版）』WILEY-VCH. ISBN 978-3-527-40601-2。
  24. ^アロンソ＆フィン 1968、セクション9.3。
  25. ^ボーン、マックス、ブリン＝ストイル、ロジャー・ジョン、ラドクリフ、JM (1989). 「付録 XXXII」.原子物理学. クーリエ社. ISBN 978-0-486-65984-8。
  26. ^マーミン、デイヴィッド（1984年2月）「光のない相対性理論」アメリカ物理学会誌52 ( 2): 119–124 . Bibcode : 1984AmJPh..52..119M . doi : 10.1119/1.13917 .
  27. ^ Plimpton, S.; Lawton, W. (1936). 「電荷間のクーロン力の法則の非常に正確な検証」 . Physical Review . 50 (11): 1066. Bibcode : 1936PhRv...50.1066P . doi : 10.1103/PhysRev.50.1066 .
  28. ^ Williams, E.; Faller, J.; Hill, H. (1971). 「クーロンの法則の新たな実験的検証：光子静止質量の実験的上限値」. Physical Review Letters . 26 (12): 721. Bibcode : 1971PhRvL..26..721W . doi : 10.1103/PhysRevLett.26.721 .
  29. ^ Chibisov, GV (1976). 「光子の静止質量の天体物理学的上限」.ソビエト物理学誌. 19 (7): 624. Bibcode : 1976SvPhU..19..624C . doi : 10.1070/PU1976v019n07ABEH005277 .
  30. ^ Lakes, Roderic (1998). 「光子質量と宇宙磁気ベクトルポテンシャルの実験的限界」. Physical Review Letters . 80 (9): 1826. Bibcode : 1998PhRvL..80.1826L . doi : 10.1103/PhysRevLett.80.1826 .
  31. ^ Amsler, C; Doser, M; Antonelli, M; Asner, D; Babu, K; Baer,​​ H; Band, H; Barnett, R; et al. (2008). "Review of Particle Physics⁎" (PDF) . Physics Letters B. 667 ( 1– 5 ): 1. Bibcode : 2008PhLB..667....1A . doi : 10.1016/j.physletb.2008.07.018 . hdl : 1854/LU-685594 . S2CID 227119789. 2020年6月1日時点のオリジナルよりアーカイブ( PDF) . 2017年10月26日閲覧. 概要表は2010年1月9日にWayback Machineにアーカイブされています
  32. ^ Adelberger, Eric; Dvali, Gia; Gruzinov, Andrei (2007). 「渦によって破壊される光子質量境界」. Physical Review Letters . 98 (1) 010402. arXiv : hep-ph/0306245 . Bibcode : 2007PhRvL..98a0402A . doi : 10.1103/ PhysRevLett.98.010402 . PMID 17358459. S2CID 31249827 .  
  33. ^ロスマン, T. (2003). 『すべては相対的であり、科学技術におけるその他の寓話』ジョン・ワイリー・アンド・サンズ. ISBN 978-0-471-20257-8。
  34. ^デカルト、ルネ(1637)。Discours de la methode (方法論) (フランス語)。 Imprimerie de Ian Maire。ISBN 978-0-268-00870-3。{{cite book}}:ISBN / 日付の非互換性（ヘルプ）
  35. ^フック、ロバート(1667). 『ミクログラフィア：拡大鏡による微小物体の生理学的記述、観察および調査…』ロンドン、英国:ロンドン王立協会. ISBN 978-0-486-49564-4. 2008年12月2日時点のオリジナルよりアーカイブ。2006年9月26日閲覧。{{cite book}}:ISBN / 日付の非互換性（ヘルプ）
  36. ^ホイヘンス、クリスチャン(1678)。Traité de la lumière (フランス語)。英語版はプロジェクト・グーテンベルクから入手可能です。
  37. ^ a bニュートン、アイザック(1952) [1730]. Opticks (第4版). ドーバー、ニューヨーク: Dover Publications. 第2巻、第3部、命題XII–XX; 質問25–29. ISBN 978-0-486-60205-9。{{cite book}}:ISBN / 日付の非互換性（ヘルプ）
  38. ^ Buchwald, JZ (1989). 「光の波動理論の台頭：19世紀初頭の光学理論と実験」 . Physics Today . 43 (4). シカゴ大学出版局: 78–80 . Bibcode : 1990PhT....43d..78B . doi : 10.1063/1.2810533 . ISBN 978-0-226-07886-1. OCLC  18069573 .
  39. ^マクスウェル、ジェームズ・クラーク(1865). 「電磁場の動的理論」 .王立協会哲学論文集. 155 : 459–512 . Bibcode : 1865RSPT..155..459M . doi : 10.1098/rstl.1865.0008 . S2CID 186207827 . この記事は、1864 年 12 月 8 日にマクスウェルが王立協会で発表した内容を受けて書かれたものです。
  40. ^ヘルツ、ハインリッヒ(1888)。 「ユーバー・シュトラレン・エレクトリッシャー・クラフト」。Sitzungsberichte der Preussischen Akademie der Wissenschaften (ドイツ語)。1888 年。ドイツ、ベルリン：1297 ～ 1307 年。
  41. ^「発光の周波数依存性」pp. 276ff.、§1.4「光電効果」 Alonso & Finn 1968。
  42. ^ Wien, W. (1911). 「Wilhelm Wien Nobel Lecture」 . nobelprize.org . 2011年7月15日時点のオリジナルよりアーカイブ。 2006年8月25日閲覧。
  43. ^マックス、プランク(1901)。「通常のスペクトルにおけるエネルギーの強化」。Annalen der Physik (ドイツ語)。4 (3): 553–563。Bibcode : 1901AnP...309..553P。土井：10.1002/andp.19013090310。英語翻訳
  44. ^ Planck, Max (1920). 「マックス・プランクのノーベル賞講演」 . nobelprize.org. 2011年7月15日時点のオリジナルよりアーカイブ。 2006年8月25日閲覧。
  45. ^ a b c dアインシュタイン、アルバート(1905)。「Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt」(PDF)。Annalen der Physik (ドイツ語)。17 (6): 132–148。Bibcode : 1905AnP...322..132E。土井：10.1002/andp.19053220607。2015 年 9 月 24 日にオリジナルからアーカイブ(PDF)されました。2010 年 8 月 25 日に取得。この図によれば、点光源から放射される光波のエネルギーは、より大きな体積にわたって連続的に広がるのではなく、空間の点に空間的に局在し、分割されずに移動し、全体としてのみ吸収または生成される有限数のエネルギー量子から構成されます。英語翻訳はWikisourceから入手できます。
  46. ^ a b cアインシュタイン、アルバート(1909)。"Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung" (PDF)。Physikalische Zeitschrift (ドイツ語)。10 : 817–825。2011年 6 月7日にオリジナルからアーカイブ(PDF) 。2010 年 8 月 25 日に取得。英語翻訳はWikisourceから入手できます。
  47. ^ 1921年のノーベル物理学賞授賞式におけるスヴァンテ・アレニウスの演説、1922年12月10日。オンラインテキストは[nobelprize.org]から2011年9月4日にWayback Machineにアーカイブされています。ノーベル財団2008年。アクセス日2008年12月5日。
  48. ^アインシュタイン、アルバート(1916)。 「Zur Quantentheorie der Strahlung」。Mittailungen der Physikalischen Gesellschaft zu Zürich (ドイツ語)。16：47。また、Physikalische Zeitschrift (ドイツ語)、18、121–128 (1917)。
  49. ^ a bミリカン、ロバート・A. (1924). 「ロバート・A・ミリカンのノーベル賞講演」 . 2011年7月15日時点のオリジナルよりアーカイブ。2006年8月25日閲覧。
  50. ^ヘンドリー、J. (1980). 「光の波動粒子二重性と量子論に対する態度の発展、1900–1920年」Annals of Science . 37 (1): 59– 79. doi : 10.1080/00033798000200121 .
  51. ^コンプトン、アーサー(1923). 「軽元素によるX線散乱の量子理論」 .フィジカル・レビュー. 21 (5): 483– 502. Bibcode : 1923PhRv...21..483C . doi : 10.1103/PhysRev.21.483 . 2018年1月29日時点のオリジナルよりアーカイブ。 2020年11月8日閲覧。
  52. ^ボーア, ニールス;クレイマース, ヘンドリック・アンソニー;スレーター, ジョン・C. (1924). 「放射線の量子論」.哲学雑誌. 47 (281): 785– 802. doi : 10.1080/14786442408565262 .また、Zeitschrift für Physik (ドイツ語)、24、p. 69年（1924年）。
  53. ^ハワード、ドン（2004年12月）「『コペンハーゲン解釈』を発明したのは誰か？神話研究」『科学哲学』71 (5): 669–682 . doi : 10.1086/425941 . ISSN 0031-8248 . JSTOR 10.1086/425941 . S2CID 9454552 .   
  54. ^ a b cペイス、A.（1982年）『微妙なる主：アルバート・アインシュタインの科学と生涯』オックスフォード大学出版局、ISBN 978-0-19-853907-0。
  55. ^ハイゼンベルク、ヴェルナー(1933). 「ハイゼンベルクのノーベル講演」 . 2011年7月19日時点のオリジナルよりアーカイブ。2006年9月11日閲覧。
  56. ^ Mandel, Leonard (1976). Wolf, E. (ed.). II 半古典的放射理論の賛否両論. Progress in Optics . Vol. 13. North-Holland. pp.  27– 69. Bibcode : 1976PrOpt..13...27M . doi : 10.1016/S0079-6638(08)70018-0 . ISBN 978-0-444-10806-7。{{cite book}}:|journal=無視されました (ヘルプ)
  57. ^ Grangier, P.; Roger, G.; Aspect, A. (1986). 「ビームスプリッターにおける光子反相関効果の実験的証拠：単一光子干渉の新たな解明」. Europhysics Letters . 1 (4): 173– 179. Bibcode : 1986EL......1..173G . CiteSeerX 10.1.1.178.4356 . doi : 10.1209/0295-5075/1/4/004 . S2CID 250837011 .  
  58. ^ Thorn, JJ; Neel, MS; Donato, VW; Bergreen, GS; Davies, RE; Beck, M. (2004). 「学部生実験室における光の量子挙動の観察」(PDF) . American Journal of Physics . 72 (9): 1210– 1219. Bibcode : 2004AmJPh..72.1210T . doi : 10.1119/1.1737397 . 2016年2月1日時点のオリジナルよりアーカイブ(PDF) . 2009年6月29日閲覧.
  59. ^ Kragh, Helge (2000-12-01). 「マックス・プランク：消極的な革命家」. Physics World . 13 (12): 31– 36. doi : 10.1088/2058-7058/13/12/34 .
  60. ^プランク、マックス (1922). 「Googleブックス経由」 ​​. 『量子論の起源と発展』 . クラレンドン・プレス – インターネット・アーカイブ経由 (archive.org, 2007-03-01).
  61. ^ Lewis, Gilbert N. (1926年12月18日). 「光子の保存」. Nature . 118 (2981): 874– 875. Bibcode : 1926Natur.118..874L . doi : 10.1038/118874a0 . eISSN 1476-4687 . S2CID 4110026 .  
  62. ^ヴィラード、ポール・ウルリッヒ(1900)。 「ラジウムのレイヨン陰極とレイヨンの反射と反射」。Comptes Rendus des Séances de l'Académie des Sciences (フランス語)。130：1010～ 1012。
  63. ^ヴィラード、ポール・ウルリッヒ(1900)。 「ラジウムのシュール・レヨンヌマン」。Comptes Rendus des Séances de l'Académie des Sciences (フランス語)。130 : 1178–1179。
  64. ^ Rutherford, Ernest ; Andrade, Edward NC (1914). 「ラジウムBからの軟ガンマ線の波長」 . Philosophical Magazine . 27 (161): 854– 868. doi : 10.1080/14786440508635156 . 2020年3月8日時点のオリジナルよりアーカイブ。 2019年8月25日閲覧。
  65. ^リドル、アンドリュー (2015). 『現代宇宙論入門』 ジョン・ワイリー・アンド・サンズ. p. 16. ISBN 978-1-118-69025-3. 2024年5月13日時点のオリジナルよりアーカイブ。2017年2月27日閲覧。
  66. ^ Taylor, GI (1909). 「微弱光による干渉縞」 .ケンブリッジ哲学協会数学紀要. 15 : 114. 2024年12月7日閲覧。
  67. ^ Saleh, BEA & Teich, MC (2007). 『フォトニクスの基礎』 Wiley. ISBN 978-0-471-35832-9。
  68. ^ Newton, TD; Wigner, EP (1949). 「素粒子の局在状態」(PDF) . Reviews of Modern Physics . 21 (3): 400– 406. Bibcode : 1949RvMP...21..400N . doi : 10.1103/RevModPhys.21.400 . 2023年5月16日時点のオリジナルよりアーカイブ(PDF) . 2023年6月21日閲覧.
  69. ^ Bialynicki-Birula, I. (1994). 「光子の波動関数について」 . Acta Physica Polonica A. 86 ( 1–2 ) : 97– 116. Bibcode : 1994AcPPA..86...97B . doi : 10.12693/APhysPolA.86.97 .
  70. ^ Sipe, JE (1995). 「光子波動関数」. Physical Review A. 52 ( 3): 1875– 1883. Bibcode : 1995PhRvA..52.1875S . doi : 10.1103/PhysRevA.52.1875 . PMID 9912446 . 
  71. ^ Bialynicki-Birula, I. (1996). V 光子波動関数. Progress in Optics . Vol. 36. pp.  245– 294. Bibcode : 1996PrOpt..36..245B . doi : 10.1016/S0079-6638(08)70316-0 . ISBN 978-0-444-82530-8. S2CID  17695022 .{{cite book}}:|journal=無視されました (ヘルプ)
  72. ^ a b c Scully, MO; Zubairy, MS (1997).量子光学. ケンブリッジ, イギリス: ケンブリッジ大学出版局. ISBN 978-0-521-43595-6. 2024年5月13日時点のオリジナルよりアーカイブ。2016年10月6日閲覧。
  73. ^ Busch, Paul ; Lahti, Pekka ; Werner, Reinhard F. (2013-10-17). 「ハイゼンベルクの誤差-擾乱関係の証明」 ( PDF) . Physical Review Letters . 111 (16) 160405. arXiv : 1306.1565 . Bibcode : 2013PhRvL.111p0405B . doi : 10.1103/PhysRevLett.111.160405 . ISSN 0031-9007 . PMID 24182239. S2CID 24507489 .   
  74. ^ Appleby, David Marcus (2016年5月6日). 「量子エラーと擾乱：Busch、Lahti、Wernerへの応答」 . Entropy . 18 (5): 174. arXiv : 1602.09002 . Bibcode : 2016Entrp..18..174A . doi : 10.3390/e18050174 .
  75. ^ Landau, Lev D. ; Lifschitz, Evgeny M. (1977).量子力学：非相対論的理論. 第3巻（第3版）. Pergamon Press . ISBN 978-0-08-020940-1. OCLC  2284121 .
  76. ^ Busch, P.; Grabowski, M.; Lahti, PJ (1995年1月). 「POV測度を恐れるのは誰か？量子位相観測量への統一的アプローチ」Annals of Physics . 237 (1): 1– 11. Bibcode : 1995AnPhy.237....1B . doi : 10.1006/aphy.1995.1001 .
  77. ^ボーズ、サティエンドラ・ナス(1924)。 「プランクス・ゲセッツとリヒトクアンテン仮説」。Zeitschrift für Physik (ドイツ語)。26 (1): 178–181。Bibcode : 1924ZPhy...26..178B。土井：10.1007/BF01327326。S2CID 186235974。 
  78. ^アインシュタイン、アルバート(1924)。 「理想的なガスの量論」。Sitzungsberichte der Preussischen Akademie der Wissenschaften (ベルリン)、Physikalisch-mathematische Klasse (ドイツ語)。1924 : 261–267 .
  79. ^アインシュタイン、アルバート(1925)。Quantentheorie des einaomigen Idealen Gases、Zweite Abhandlung (ドイツ語)。 Vol. 1925. pp.  3–14 . doi : 10.1002/3527608958.ch28。ISBN 978-3-527-60895-9。{{cite book}}: ;無視されました (ヘルプ)ISBN / 日付の非互換性（ヘルプ）|journal=
  80. ^ Anderson, MH; Ensher, JR; Matthews, MR; Wieman, Carl E .; Cornell, Eric Allin (1995). 「希薄原子蒸気中のボーズ・アインシュタイン凝縮の観測」. Science . 269 ( 5221 ): 198– 201. Bibcode : 1995Sci...269..198A . doi : 10.1126/science.269.5221.198 . JSTOR 2888436. PMID 17789847. S2CID 540834 .   
  81. ^ Cuneo, Michael (1999年2月18日). 「物理学者、光速を遅らせる」 . Harvard Gazette . 2000年10月15日時点のオリジナルよりアーカイブ。2023年12月7日閲覧。
  82. ^ 「光は物質に変わり、止まり、そして移動する」 www.photonics.com 。 2019年4月2日時点のオリジナルよりアーカイブ。 2023年12月7日閲覧。
  83. ^ストリーター, RF; ワイトマン, AS (1989). PCT, スピンと統計, そしてその他諸々 . アディソン・ウェスリー. ISBN 978-0-201-09410-7。
  84. ^アインシュタイン、アルバート(1916)。 「放射と吸収の量理論」。Verhandlungen der Deutschen Physikalischen Gesellschaft (ドイツ語)。18 : 318–323。Bibcode : 1916DPhyG..18..318E。
  85. ^ Wilson, J.; Hawkes, FJB (1987).レーザー：原理と応用. ニューヨーク: Prentice Hall. 第1.4節. ISBN 978-0-13-523705-2。
  86. ^アインシュタイン、アルバート(1916)。 「放射と吸収の量理論」。Verhandlungen der Deutschen Physikalischen Gesellschaft (ドイツ語)。18 : 318–323。Bibcode : 1916DPhyG..18..318E。p. 322: Die Konstanten and würden sich direkt berechnen lassen, wenn wir im Besitz einer im Sinne der Quantenhypothese modifizierten Elektrodynamik und Mechanik wären."あメートルn{\displaystyle A_{m}^{n}}Bメートルn{\displaystyle B_{m}^{n}}
  87. ^ディラック, ポール・A・M (1926). 「量子力学の理論について」 . Proceedings of the Royal Society A. 112 ( 762): 661– 677. Bibcode : 1926RSPSA.112..661D . doi : 10.1098/rspa.1926.0133 .
  88. ^ a bディラック, ポール AM (1927). 「放射線の放出と吸収の量子論」 . Proceedings of the Royal Society A. 114 ( 767): 243– 265. Bibcode : 1927RSPSA.114..243D . doi : 10.1098/rspa.1927.0039 .
  89. ^ a bディラック, ポール AM (1927b). 「分散の量子理論」 . Proceedings of the Royal Society A. 114 ( 769): 710– 728. Bibcode : 1927RSPSA.114..710D . doi : 10.1098/rspa.1927.0071 .
  90. ^ハイゼンベルク、ヴェルナー;パウリ、ヴォルフガング(1929)。 「ヴェレンフェルダーの知識」。Zeitschrift für Physik (ドイツ語)。56 ( 1–2 ): 1. Bibcode : 1929ZPhy...56....1H。土井：10.1007/BF01340129。S2CID 121928597。 
  91. ^ハイゼンベルク、ヴェルナー;パウリ、ヴォルフガング(1930)。 「ヴェレンフェルダーの知識」。Zeitschrift für Physik (ドイツ語)。59 ( 3–4 ): 139。Bibcode : 1930ZPhy...59..168H。土井：10.1007/BF01341423。S2CID 186219228。 
  92. ^フェルミ, エンリコ(1932). 「放射線の量子論」.現代物理学レビュー. 4 (1): 87. Bibcode : 1932RvMP....4...87F . doi : 10.1103/RevModPhys.4.87 .
  93. ^マックス生まれ（1926年）。 「Zur Quantenmechanik der Stossvorgänge」。Zeitschrift für Physik (ドイツ語)。37 (12): 863–867。Bibcode : 1926ZPhy...37..863B。土井: 10.1007/BF01397477。S2CID 119896026。 
  94. ^マックス生まれ（1926年）。 「Quantenmechanik der Stossvorgänge」。Zeitschrift für Physik (ドイツ語)。38 ( 11–12 ): 803。Bibcode : 1926ZPhy...38..803B。土井：10.1007/BF01397184。S2CID 126244962。 
  95. ^ペイス、A. (1986). 『内向きの境界：物理世界における物質と力について』オックスフォード大学出版局. p. 260. ISBN 978-0-19-851997-3。具体的には、ボーン氏は、点状の光子がマクスウェル方程式に従うゴーストフィールドによって確率的に誘導されるという「ゴーストフィールド」理論を開発しようとした、アインシュタインの未発表の試みに触発されたと主張した。
  96. ^デバイ、ピーター(1910)。"Der Wahrscheinlichkeitsbegriff in der The Orie der Strahlung"。Annalen der Physik (ドイツ語)。33 (16): 1427–1434。Bibcode : 1910AnP...338.1427D。土井：10.1002/andp.19103381617。2020-03-14 のオリジナルからアーカイブ。2019年8月25日に取得。
  97. ^生まれました、マックス;ハイゼンベルク, ヴェルナー;ジョーダン、パスクアル（1925年）。 「クァンテンメカニックⅡ」。Zeitschrift für Physik (ドイツ語)。35 ( 8–9 ): 557– 615。Bibcode : 1926ZPhy...35..557B。土井：10.1007/BF01379806。S2CID 186237037。 
  98. ^ Jaeger, Gregg (2019). 「仮想粒子は実在性が低いのか？」(PDF) .エントロピー. 21 (2): 141. Bibcode : 2019Entrp..21..141J . doi : 10.3390/e21020141 . PMC 7514619. PMID 33266857. 2023年6月11日時点のオリジナルよりアーカイブ(PDF) . 2021年5月19日閲覧.  
  99. ^ジー、アンソニー（2003年）『量子場理論入門』プリンストン大学出版局（ニュージャージー州）ISBN 0-691-01019-6. OCLC  50479292 .
  100. ^ Itzykson, C.; Zuber, J.-B. (1980).量子場の理論. McGraw-Hill. 光子-光子散乱セクション7–3–1、再正規化章8–2. ISBN 978-0-07-032071-0。
  101. ^ Weiglein, G. (2008). 「ILCにおける電弱物理学」. Journal of Physics: Conference Series . 110 (4) 042033. arXiv : 0711.3003 . Bibcode : 2008JPhCS.110d2033W . doi : 10.1088/1742-6596/110/4/042033 . S2CID 118517359 . 
  102. ^ a bライダー、LH（1996年）『量子場の理論』（第2版）イギリス：ケンブリッジ大学出版局。ISBN 978-0-521-47814-4。
  103. ^シェルドン・グラショウのノーベル賞講演Archived 2008-04-18 at the Wayback Machine、1979年12月8日配信。
  104. ^アブドゥッサラム・ノーベル賞講演Archived 2008-04-18 at the Wayback Machine、1979年12月8日配信。
  105. ^スティーブン・ワインバーグのノーベル賞講演Archived 2008-04-18 at the Wayback Machine、1979年12月8日。
  106. ^例えば、ヒューズ著『素粒子』（第2版、1985年）第14章。ケンブリッジ大学出版局。ISBN 978-0-521-26092-3。
  107. ^ Bauer, TH; Spital, RD; Yennie, DR; Pipkin, FM (1978). 「高エネルギー相互作用における光子のハドロン的性質」Reviews of Modern Physics . 50 (2): 261. Bibcode : 1978RvMP...50..261B . doi : 10.1103/RevModPhys.50.261 .
  108. ^桜井, JJ (1960). 「強い相互作用の理論」Annals of Physics . 11 (1): 1– 48. Bibcode : 1960AnPhy..11....1S . doi : 10.1016/0003-4916(60)90126-3 .
  109. ^ Walsh, TF; Zerwas, P. (1973). 「パートン模型における2光子過程」. Physics Letters B. 44 ( 2): 195. Bibcode : 1973PhLB...44..195W . doi : 10.1016/0370-2693(73)90520-0 .
  110. ^ Witten, E. (1977). 「ゲージ理論における光子-光子散乱の異常断面積」.核物理学B. 120 ( 2): 189– 202. Bibcode : 1977NuPhB.120..189W . doi : 10.1016/0550-3213(77)90038-4 .
  111. ^ Nisius, R. (2000). 「深部非弾性電子–光子散乱による光子構造」. Physics Reports . 332 ( 4–6 ): 165–317 . arXiv : hep-ex/9912049 . Bibcode : 2000PhR...332..165N . doi : 10.1016/S0370-1573(99)00115-5 . S2CID 119437227 . 
  112. ^例えば、ダンラップ（RA）著『原子核と粒子の物理学入門』（ 2004年）第10.1節、ブルックス／コール社、ISBN 978-0-534-39294-9。
  113. ^電子質量への放射補正（7–1–2節）、異常磁気モーメント（7–2–1節）、ラムシフト（7–3–2節）、およびポジトロニウムの超微細分裂（10–3節）については、 Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory . McGraw-Hill. ISBN 978-0-07-032071-0。
  114. ^例えば、Stephani, H.; Stewart, J. (1990). General Relativity: An Introduction to the Theory of Gravitational Field . Cambridge University Press. pp. 86 ff, 108 ff. ISBN 9.1節（光子の重力への寄与）と10.5節（光に対する重力の影響） 978-0-521-37941-0。
  115. ^ポラリトンのセクション10.10.1、ラマン散乱とブリルアン散乱のセクション10.11.3、 Patterson, JD; Bailey, BC (2007). Solid-State Physics: Introduction to the Theory . Springer . ISBN 978-3-540-24115-7。
  116. ^ 「太陽内部」マーシャル宇宙飛行センター：太陽物理学アメリカ航空宇宙委員会2024年12月4日閲覧。
  117. ^クーペリス, テオ; クーン, カール F. (2007). 『宇宙の探求』 ジョーンズ・アンド・バートレット・カナダ. p. 102. ISBN 978-0-7637-4387-1. 2024年5月12日時点のオリジナルよりアーカイブ。2020年11月29日閲覧。
  118. ^例えば、 Pine, SH; Hendrickson, JB; Cram, DJ; Hammond, GS (1980). Organic Chemistry (4th ed.). McGraw-Hill. ISBN 11-5 C を参照 978-0-07-050115-7。
  119. ^ 1967年12月12日にG. Waldが行ったノーベル賞講演、nobelprize.orgでオンラインで閲覧可能：「視覚興奮の分子的基礎」Wayback Machineに2016年4月23日アーカイブ。
  120. ^光電子増倍管セクション1.1.10、CCDセクション1.1.8、ガイガーカウンターセクション1.3.2.1、 Kitchin, CR (2008). Astrophysical Techniques . Boca Raton, Florida: CRC Press. ISBN 978-1-4200-8243-2。
  121. ^ウェイマス、ジョン（1971年）『放電ランプ』、マサチューセッツ州ケンブリッジ：MIT出版、ISBN 978-0-262-23048-3。
  122. ^ Denk, W. ; Svoboda, K. (1997). 「光子の優位性：多光子イメージングが単なる仕掛け以上のものとなる理由」 . Neuron . 18 (3): 351– 357. doi : 10.1016 / S0896-6273(00)81237-4 . PMID 9115730. S2CID 2414593 .  
  123. ^ Lakowicz, JR (2006).蛍光分光法の原理. Springer. pp. 529 ff. ISBN 978-0-387-31278-1。
  124. ^ Jennewein, T.; Achleitner, U.; Weihs, G.; Weinfurter, H.; Zeilinger, A. (2000). 「高速かつコンパクトな量子乱数発生器」. Review of Scientific Instruments . 71 (4): 1675– 1680. arXiv : quant-ph/9912118 . Bibcode : 2000RScI...71.1675J . doi : 10.1063/1.1150518 . S2CID 13118587 . 
  125. ^ Stefanov, A.; Gisin, N.; Guinnard, O.; Guinnard, L.; Zbiden, H. (2000). 「光量子乱数発生器」. Journal of Modern Optics . 47 (4): 595– 598. doi : 10.1080/095003400147908 .
  126. ^ 量子光学の様々な分野に関する入門レベルの資料は、 Fox, M. (2006). Quantum Optics: An Introduction . Oxford University Press. ISBNに掲載されています。 978-0-19-856673-1– Google ブックス経由。
  127. ^ Hignett, Katherine (2018年2月16日). 「物理学が量子コンピューティング革命の原動力となる新たな光の形を創造」 . Newsweek . 2021年4月25日時点のオリジナルよりアーカイブ。 2018年2月17日閲覧。
  128. ^ Liang, Qi-Yu; et al. (2018年2月16日). 「量子非線形媒質における3光子束縛状態の観測」 . Science . 359 (6377): 783– 786. arXiv : 1709.01478 . Bibcode : 2018Sci...359..783L . doi : 10.1126 / science.aao7293 . PMC 6467536. PMID 29449489 .  

さらに読む

発行日順
単一光子による教育
  • ウィキクォートにおける光子に関する引用
  • ウィクショナリーにおける光子の辞書的定義
  • ウィキメディア・コモンズにおけるPhoton関連メディア
「 https://en.wikipedia.org/w/index.php?title=Photon&oldid=1325412255#Physical_properties」から取得