利益最大化
利潤最大化の例図: 供給と需要のグラフでは、 の産出量は(限界収入) と(限界費用)の交点です。この産出量レベルで生産する企業は、利潤を最大化すると言われています。赤い部分で示すように、生産量が均衡量 ( ) より少ない場合、は( )より大きくなり、利潤は最大化されません。得られる収入が支払う費用より大きくなるため、企業にとって利潤を最大化するために産出量を上げることは利益になります。しかし、青い部分で示すように、産出量レベルが( ) より大きい場合、追加生産されるユニットによって全体の費用が増加するため、企業全体の利潤は減少します。ここでも利潤は最大化されず、企業は利潤を最大化するために産出量を下げる必要があります。質問∗{\displaystyle Q^{*}}氏{\displaystyle {\text{MR}}}MC{\displaystyle {\text{MC}}}氏＝MC{\displaystyle {\text{MR}}={\text{MC}}}質問∗{\displaystyle Q^{*}}氏{\displaystyle {\text{MR}}}MC{\displaystyle {\text{MC}}}氏>MC{\displaystyle {\text{MR}}>{\text{MC}}}質問∗{\displaystyle Q^{*}}氏<MC{\displaystyle {\text{MR}}

経済学において、利潤最大化とは、企業が総利潤（あるいは単に利潤）を最大化するように価格、投入量、産出量を決定する短期的または長期的なプロセスを指します。現在、ミクロ経済学の主流となっている新古典派経済学では、企業は（完全競争市場であろうとなかろうと）総収益と総費用の差である総利潤を最大化しようとする「合理的主体」であると想定されています。

総費用と総収益を測定することは、企業が生産のあらゆる段階における費用を決定するために必要な信頼できる情報を持たないため、しばしば非現実的です。その代わりに、企業は生産における小さな変化が収益と費用にどのような影響を与えるかを調べるという、より現実的なアプローチをとります。企業が製品を1単位追加生産した場合、その販売によって得られる追加収益は限界収益（）と呼ばれ、その単位を生産するための追加費用は限界費用（）と呼ばれます。限界収益が限界費用（ ）と等しくなるような生産量レベルの場合、企業の総利潤は最大化されていると言えます。限界収益が限界費用（）よりも大きい場合、企業は追加の利益を得るために追加の生産単位を生産できるため、総利潤は最大化されていません。言い換えれば、この場合、総利潤が最大化されるまで生産量を増やすことは、企業にとって「合理的」な利益となります。一方、限界収入が限界費用（）よりも低い場合、総利潤も最大化されません。なぜなら、生産量を1単位減らすことで総費用が総収入よりも減少するため、企業の総利潤は増加するからです。この場合、「合理的な」企業は、総利潤が最大化されるまで生産量を削減するインセンティブを持ちます。[ 1 ]氏{\displaystyle {\text{MR}}}MC{\displaystyle {\text{MC}}}氏＝MC{\displaystyle {\text{MR}}={\text{MC}}}氏>MC{\displaystyle {\text{MR}}>{\text{MC}}}氏<MC{\displaystyle {\text{MR}}

主な視点

利益最大化にはいくつかの視点があります。まず、利益は収益から費用を引いたものに等しいので、収益と費用の各変数を産出量の関数としてグラフにプロットし、その差を最大化する産出量レベルを見つけることができます（グラフではなく値の表を使用することもできます）。次に、産出量に関して収益と費用の特定の関数形がわかっている場合は、微積分を使用して産出量レベルに関して利益を最大化できます。3つに、最適化の第一条件は限界収益と限界費用を等しくするため、産出量に関する限界収益（）関数と限界費用（）関数が直接利用できる場合は、方程式またはグラフを使用してこれらを等しくすることができます。4つに、企業は、各潜在的な産出量レベルの生産コストを与える関数ではなく、各投入量の任意の組み合わせを使用することでどれだけの産出が生じるかを示す生産関数とともに、任意の量の投入を取得するためのコストを与える投入コスト関数を持つことができます。この場合、微積分を用いて、投入費用関数と生産関数を前提として、投入物の使用量に対する利益を最大化することができます。各投入物に関する第一階条件は、投入物の限界収益積（投入量の増加によって生じる製品の販売収益の増加分）と投入物の限界費用を等しくすることです。 氏{\displaystyle {\text{MR}}}MC{\displaystyle {\text{MC}}}

生産物に関して完全競争市場にある企業の場合、収益関数は単に市場価格と生産量および販売量を掛け合わせた値になりますが、販売価格と同時に生産量レベルを決める独占企業の場合、独占企業は通常利益を上げることができるため、より多くの製品を生産するでしょう。利益を最大化するには、競争市場よりも高い価格と低い生産量を設定する必要があります。しかし、収益関数は、生産量が多いほど販売価格は低くなるという事実を考慮に入れています。投入市場でも同様の特徴が当てはまります。完全競争投入市場では、企業の投入コストは単に生産に使用するために購入された量に市場で決定される単位投入コストを掛け合わせた値になりますが、独占購買企業の単位当たりの投入価格は、購入する投入量が多いほど高くなります。

短期利潤最大化と長期利潤最大化の主な違いは、長期的には物的資本を含むすべての投入量が選択変数であるのに対し、短期的には資本の量が過去の投資決定によって予め決定されている点である。いずれの場合も、労働と原材料が投入される。

基本的な定義

企業が負担するコストは、固定費と変動費の2つのグループに分類できます。固定費は短期的にのみ発生し、生産量がゼロの場合も含め、あらゆる生産量レベルで企業に発生します。固定費には、設備のメンテナンス、家賃、短期的に増減できない従業員の賃金、一般的な維持費などが含まれます。変動費は生産量に応じて変化し、製品の生産量が増えるほど増加します。生産中に消費される原材料は、このカテゴリに最も大きな影響を与えることが多く、検討中の短期間で雇用および解雇される可能性のある従業員の賃金も含まれます。固定費と変動費を合わせると、総コストになります。

収益とは、企業が通常の事業活動、通常は商品やサービスの販売（株式や債券の発行などの証券販売による金銭とは対照的）から受け取る金額です。

5つの方法論は、リード、コンバージョン率、平均売上高、平均販売数、そして平均製品利益を増加させることです。利益は最大1,000%増加させることができ、これは大企業はもちろん、個人事業主や中小企業にとっても重要です。しかし、利益の最大化は事業段階ごとに重要であり、利益分配のリターンが高まれば、賃金とモチベーションも高まります。[ 2 ]

限界費用と限界収益は、微積分アプローチを採用するかどうかに応じて、生産単位が増えるにつれて費用または収益がどれだけ変化するか、あるいは生産量に対する費用または収益の微分として定義されます。例えば、最初の定義を採用すると、企業が5単位の生産に400ドル、6単位の生産に480ドルかかる場合、6単位目の限界費用は80ドルです。逆に、6単位の生産による限界収益は、6単位の生産による収益から5単位の生産による収益（後者から前者の収益を差し引いたもの）を差し引いたものです。

総収益 - 総費用の観点

完全競争企業の総収益と総費用曲線を用いた利益最大化

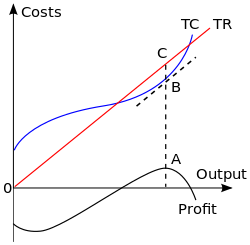
利潤を最大化する生産量を求めるには、まず、利潤は総収入（）から総費用（）を引いたものに等しいことを認識することから始めます。各量における費用と収入の表が与えられれば、方程式を計算するか、データを直接グラフにプロットすることができます。利潤を最大化する生産量とは、この差が最大となる生産量です。 TR{\displaystyle {\text{TR}}}TC{\displaystyle {\text{TC}}}

添付の図では、線形総収入曲線は、企業が財市場において完全競争者であり、したがって独自の販売価格を設定できない場合を表しています。利潤最大化の産出水準は、総収入が の高さ、総費用が の高さとなる水準として表されます。最大利潤は、線分 の長さとして測定されます。この産出水準は、総利潤曲線が最大となる水準でもあります。 C{\displaystyle {\text{C}}}B{\displaystyle {\text{B}}}CB¯{\displaystyle {\overline {\text{CB}}}}

グラフで想定されているのとは反対に、企業が産出市場において完全な競争者でない場合、製品の販売価格は、企業の最適産出量における需要曲線から読み取ることができます。この最適産出量とは、限界収入が限界費用と等しくなる量です。

限界収入と限界費用の観点

完全競争者の限界収入曲線と限界費用曲線を用いた利益最大化
独占企業による価格設定

同等の観点は、販売された各ユニットについて、限界利益（）は限界収入（）から限界費用（）を引いた値に等しいという関係に基づいています。したがって、ある産出レベルで限界収入が限界費用よりも大きい場合、限界利益は正となり、したがってより多くの量を生産する必要があります。一方、限界収入が限界費用よりも小さい場合、限界利益は負となり、より少ない量を生産する必要があります。限界収入が限界費用に等しい産出レベルでは、限界利益はゼロとなり、この量が利益を最大化する量となります。[ 3 ]限界利益が正のときに総利益が増加し、限界利益が負のときに総利益が減少するため、限界利益がゼロ（限界費用が限界収入に等しい）で、かつ産出レベルが低いか高いほど利益レベルが低くなるところで、総利益は最大値に達しなければなりません。[ 3 ]微積分学の用語で言えば、最適な産出が隣接する産出レベルよりも高い利益を持つという要件は、次のとおりです。[ 3 ]Mπ{\displaystyle {\text{M}}\pi }氏{\displaystyle {\text{MR}}}MC{\displaystyle {\text{MC}}}

d2⁡Rd⁡質問2<d2⁡Cd⁡質問2。{\displaystyle {\frac {\operatorname {d} ^{2}R}{{\operatorname {d} Q}^{2}}}}。

との交点は、次の図の点 で示されています。業界が完全競争である場合（図で想定されているように）、企業は限界収入曲線（ ）と同一の需要曲線（ ）に直面します。これは、業界の需要と供給によって決まる価格における水平線です。平均総費用は曲線 で表されます。総経済利潤は、長方形 の面積で表されます。最適数量（）は、最初の図の最適数量と同じです。 氏{\displaystyle {\text{MR}}}MC{\displaystyle {\text{MC}}}あ{\displaystyle {\text{A}}}D{\displaystyle {\text{D}}}氏{\displaystyle {\text{MR}}}航空管制局{\displaystyle {\text{ATC}}}PABC¯{\displaystyle {\overline {\text{PABC}}}}質問{\displaystyle Q}

企業が独占企業である場合、限界収入曲線は右下がりの市場需要曲線に基づくため、次のグラフに示すように負の傾きを持つ。グラフで と示される最適産出量とは、限界費用が限界収入に等しくなる産出量水準である。その産出量を誘発する価格は、その産出量における需要曲線の高さ（ と表記）である。 質問メートル{\displaystyle Q_{m}}Pメートル{\displaystyle P_{m}}

利潤最大化のための産出水準の一般的な導出は、以下の手順で与えられる。まず、代表的企業が自社の利潤に関する完全情報を持っていると仮定する。これは以下のように表される。 私{\displaystyle i}

π私＝TR私−TC私{\displaystyle \pi _{i}={\text{TR}}_{i}-{\text{TC}}_{i}}

ここで、は総収入、は総費用を表します。上記の式は次のように書き直すことができます。 TR{\displaystyle {\text{TR}}}TC{\displaystyle {\text{TC}}}

π私＝p私⋅q私−c私⋅q私{\displaystyle \pi _{i}=p_{i}\cdot q_{i}-c_{i}\cdot q_{i}}

ここで、は価格（限界収入）、数量、限界費用を表します。企業は数量に関して利潤を最大化し、利潤最大化水準の産出を実現します。 p{\displaystyle p}q{\displaystyle q}c{\displaystyle c}

（∂π私）（∂q私）＝p私−c私＝0{\displaystyle {\frac {\left(\partial \pi _{i}\right)}{\left(\partial q_{i}\right)}}=p_{i}-c_{i}=0}

したがって、利益を最大化する生産レベルは、限界費用に等しい限界収益です。 p私{\displaystyle p_{i}}c私{\displaystyle c_{i}}

競争的ではあるが完全には競争的ではない環境では、より複雑な利益最大化ソリューションにはゲーム理論の利用が必要になります。

収益の最大化が同等の場合

場合によっては、企業の需要と費用の条件により、ある最大値までのすべての生産レベルで限界利益がゼロより大きくなることがあります。[ 4 ]この場合、限界利益はその最大値に達した直後にゼロに急落します。したがってこの規則は、出力を最大レベルで生産する必要があることを意味し、これは収益を最大化するレベルでもあります。[ 4 ]言い換えれば、利益を最大化する数量と価格は限界収入をゼロに設定することによって決定でき、これは出力が最大になったときに発生します。総収入曲線が最大値に達したとき、限界収入はゼロになります。定期便を例に挙げましょう。すべての座席が埋まるまでは、さらに 1 人の乗客を乗せる限界費用はごくわずかです。航空会社はすべての座席を埋めることによって利益を最大化します。 Mπ＝0{\displaystyle {\text{M}}\pi =0}

現実世界で利益を最大化する

現実の世界では、利益最大化を達成するのは容易ではありません。企業はMR（利潤率）の観点から、最後に販売した商品の限界所得と限界費用を正確に把握する必要があります。

財の需要の価格弾力性は、他の企業の反応に依存します。自社だけが価格を引き上げている場合、需要は弾力的になります。一方、ある企業が価格を引き上げ、他の企業もそれに追随した場合、需要は非弾力的になる可能性があります。

企業は予測に基づいて利益の最大化を目指すことができます。価格上昇によって需要がわずかに減少する場合、企業は需要が弾力的になる前に可能な限り価格を引き上げることができます。一般的に、需要は価格以外にも多くの要因によって発生する可能性があるため、需要に応じて価格の影響を変えることは困難です。

企業には他の目標や考慮事項がある場合もあります。例えば、企業は市場シェア拡大を目指して、最大利益よりも低い利益率を選択する場合があります。価格の引き上げは短期的には利益を最大化するため、より多くの企業の市場参入を促すことになります。

多くの企業は、労働力の安価な海外拠点への生産移転によってコスト削減を図っています（例：ナイキ）。しかし、生産ラインを海外に移転すると、不要な輸送コストが発生する可能性があります。製品の生産と販売を市場に近い場所で行うことで需要の最適化は図れますが、生産コストが大幅に高くなる場合は、適切な選択とは言えません。

ツール

利益分析
販売したすべての製品・サービスの事業コストを定期的に記録・分析します。販売した商品・サービスに関連する人件費、材料費、輸送費、広告費、保管費など、様々な項目があり、これらも経費となります。
ビジネスインテリジェンスツール
企業が業務に関連するすべてのコストとその正確性を明確に把握できるように、すべての財務情報を統合して経費報告書を記録する必要がある場合があります。
計画と実際の実行
販売・オペレーション計画プロセスを支援する「What-if」ソリューションを導入する際には、サプライチェーン、在庫管理、販売プロセスなど、企業のオペレーションに関する知識が役立ちます。企業計画が実現不可能にならないように、制約を設ける必要があります。

総費用の変化と利益最大化

企業は限界収入が限界費用に等しいところで事業を運営することで利潤を最大化する。これは新古典派理論で規定されており、新古典派理論では、企業は利潤を最大化することで産出量と投入量の水準を決定し、価格が限界費用に等しい条件を満たす。[ 5 ]短期的には、固定費の変化は利潤最大化の産出量や価格に影響を与えない。[ 6 ]企業は短期固定費を埋没費用として扱うだけで、これまで通りに事業を継続する。[ 7 ]これは図で確認できる。総費用と総収益の観点を示した図を用いると、企業は総費用線と総収益線の傾きが等しい点で利潤を最大化する。[ 4 ]固定費が増加すると、総費用曲線は変化分だけ上方に硬直的にシフトする。[ 4 ]総収益曲線や総費用曲線の形状には影響しない。したがって、利潤最大化の産出量は同じままである。この点は、限界収入と限界費用の観点の図を用いて説明することもできます。固定費の変化は、これらの曲線の位置や形状に影響を与えません。[ 4 ]簡単に言えば、利潤は総費用と関連していますが、企業は利潤を最大化するために最大利潤（の最大値）まで生産することで利潤を最大化できます。しかし、総費用が増加した場合、利潤の最大化は変化しません。総費用の増加は必ずしも限界費用を変えるわけではないため、限界費用が同じであれば、企業は依然として（）単位まで生産することで利潤を最大化できます。長期的には、競争均衡下では企業の期待利潤は理論的にはゼロになります。完全競争がある場合、市場は利潤をゼロにするように調整するはずです。利潤がゼロでない状況では、何らかの形の長期不均衡、または参入障壁などの非競争状態（企業間の完全競争がない場合）が見られると予想されます。[ 5 ]利益＝TR−TC{\displaystyle {\text{利益}}={\text{TR}}-{\text{TC}}}TR−TC{\displaystyle {\text{TR}}-{\text{TC}}}氏＝MC＝価格{\displaystyle {\text{MR}}={\text{MC}}={\text{価格}}}

マークアップ価格設定

企業の最適な生産量を決定する手法を用いることに加え、完全競争ではない企業は、利潤を最大化するように価格を設定することも可能である（与えられた需要曲線に沿って価格を設定することは、その曲線上の好ましい点を選択することを意味し、これは生産量と販売量を選択することと等価である）。利潤最大化条件は、上記の観点よりも「より適用しやすい」形式や経験則で表現することができる。[ 8 ]最初のステップは、限界収入の式を次のように書き直すことである。

氏＝ΔTRΔ質問＝PΔ質問+質問ΔPΔ質問＝P+質問ΔPΔ質問{\displaystyle {\begin{aligned}{\text{MR}}=&{\frac {\Delta {\text{TR}}}{\Delta Q}}\\=&{\frac {P\Delta Q+Q\Delta P}{\Delta Q}}\\=&P+{\frac {Q\Delta P}{\Delta Q}}\\\end{aligned}}}

ここで、と はそれぞれ価格と数量の新旧値の中間点を指します。[ 8 ]生産量1単位の増加による限界収益は2つの部分から成ります。1つ目は、企業が追加ユニットの販売から得る収益、つまり と表される収益です。追加ユニットは限界ユニットと呼ばれます。[ 9 ] 1ユニットを追加生産し、それを価格で販売すると、の収益が得られます。さらに、「企業がより高い価格で販売できたはずのユニットで失う収益」[ 9 ]を考慮する必要があります。つまり、すべてのユニットの価格が、ユニットを追加販売する努力によって引き下げられなかった場合の収益です。収益を失ったこれらのユニットは、限界下ユニットと呼ばれます。[ 9 ]つまり、追加ユニットの販売は価格のわずかな下落をもたらし、販売されたすべてのユニットの収益が だけ減少します。したがって、 となります。ここで は、企業の顧客の需要曲線を特徴付ける需要の価格弾力性であり、負です。 と設定すると となり、となります。したがって、最適なマークアップ規則は次のようになります。 P{\displaystyle P}Q{\displaystyle Q}PΔQ{\displaystyle P\Delta Q}P{\displaystyle P}P{\displaystyle P}Q⋅(ΔPΔQ){\displaystyle Q\cdot \left({\frac {\Delta P}{\Delta Q}}\right)}MR=P+Q⋅ΔPΔQ=P+P⋅QP⋅ΔPΔQ=P+PPED{\displaystyle {\text{MR}}=P+Q\cdot {\frac {\Delta P}{\Delta Q}}=P+P\cdot {\frac {Q}{P}}\cdot {\frac {\Delta P}{\Delta Q}}=P+{\frac {P}{\text{PED}}}}PED{\displaystyle {\text{PED}}}MC=MR{\displaystyle {\text{MC}}={\text{MR}}}MC=P+PPED{\displaystyle {\text{MC}}=P+{\frac {P}{\text{PED}}}}P−MCP=−1PED{\displaystyle {\frac {P-{\text{MC}}}{P}}={\frac {-1}{\text{PED}}}}P=MC1+(1PED){\displaystyle P={\frac {MC}{1+\left({\frac {1}{\text{PED}}}\right)}}}

(P−MC)P=1(−PED){\displaystyle {\frac {\left(P-{\text{MC}}\right)}{P}}={\frac {1}{\left(-{\text{PED}}\right)}}}
または同等
P=PED1+PED⋅MC{\displaystyle P={\frac {\text{PED}}{1+{\text{PED}}}}\cdot {\text{MC}}}. [ 10 ] [ 11 ]

言い換えれば、限界費用を超える価格のマークアップの大きさは、財の価格弾力性の絶対値と反比例するという法則である。[ 10 ]

最適マークアップ則は、非競争企業が市場需要曲線の弾力性領域で生産を行うことも示唆している。限界費用は正である。項が正となるのは、がとの間（つまり、その生産量レベルで需要が弾力性がある場合）のみである。 [ 12 ]この結果の背後にある直感は、需要がある値で非弾力性である場合、の減少は比例以上に増加し、それによって収益が増加するということである。つまり、が減少すれば総費用も減少するため、収益の増加と費用の減少が相まって利益が増加する。したがって、は可能な限り最高の利益をもたらさない。 PED1+PED{\displaystyle {\frac {PED}{1+{\text{PED}}}}}P>0{\displaystyle P>0}PED{\displaystyle {\text{PED}}}−1{\displaystyle -1}−∞{\displaystyle -\infty }Q1{\displaystyle Q_{1}}Q{\displaystyle Q}P{\displaystyle P}P⋅Q{\displaystyle P\cdot Q}Q{\displaystyle Q}Q1{\displaystyle Q_{1}}

労働の限界生産性、労働の限界収益生産性、そして利潤最大化

一般的な規則は、企業が限界収益が限界費用に等しい量の産出を行うことで利益を最大化するというものです。利益最大化の問題は投入側からもアプローチできます。つまり、利益を最大化する可変投入の使用法は何か、ということです。[ 13 ]利益を最大化するために、企業は「投入の限界収益がその限界費用に等しい点まで」投入の使用法を増やす必要があります。[ 14 ]数学的には、利益最大化規則は であり、下付き文字は一般的に想定される可変投入である労働を表します。 MRPL=MCL{\displaystyle {\text{MRP}}_{L}={\text{MC}}_{L}}L{\displaystyle _{L}}

限界収益生産物とは、変数入力の単位変化あたりの総収益の変化、つまり、 です。 MRPL=ΔTRΔL{\displaystyle {\text{MRP}}_{L}={\frac {\Delta {\text{TR}}}{\Delta L}}}

MRPL{\displaystyle {\text{MRP}}_{L}}は限界収入と労働の限界生産性の積です。 MRPL=MR⋅MPL{\displaystyle {\text{MRP}}_{L}={\text{MR}}\cdot {\text{MP}}_{L}}

批判

生産者余剰の最大化は、場合によっては消費者余剰を減少させる可能性がある。[ 15 ]生産者利益最大化のいくつかの形態は反競争的行為とみなされ、競争法によって規制されている。[ 15 ]短期的な生産者利益の最大化は長期的な生産者利益を減少させる可能性があり、これはダンピングなどの略奪的価格設定によって利用される可能性がある。[ 16 ]

政府の規制

市場割当は市場における企業の力を反映しており、企業が市場を独占することは非常に一般的であり、過度の力は非香港的行動の動機となることが多々あります。略奪的価格設定、抱き合わせ、不当な価格吊り上げなどの行動は、市場における独占企業の過剰な力の危機を反映しています。企業が権力を乱用して利益を最大化するのを防ぐため、政府はしばしば介入してその動きを阻止します。その主な例は、ほとんどの業界独占を事実上違法とする反トラスト規制です。この規制により、企業自体は経済的に苦しむ場合でも、消費者はサービスを提供する企業とより良い関係を築くことができます。

参照

注記

  1. ^カール・E・ケース、レイ・C・フェア、シャロン・M・オスター（2012年）、経済学原理（第10版）、プレンティス・ホール、  pp.180-181
  2. ^ entrepreneur.com
  3. ^ a b cリプシー (1975). 245–247ページ。
  4. ^ a b c d eサミュエルソン、Wとマークス、S（2003）。p. 47。
  5. ^ a bデサイ、M（2017）。
  6. ^サミュエルソン、Wとマークス、S（2003）。52ページ。
  7. ^ランズバーグ、S（2002）。
  8. ^ a b Pindyck, RとRubinfeld, D (2001) p. 333.
  9. ^ a b c Besanko, D. および Beautigam, R, (2001) p. 408.
  10. ^ a bサミュエルソン、Wとマークス、S（2003）。p.103–05。
  11. ^ Pindyck, RとRubinfeld, D (2001) p.341。
  12. ^ BesankoとBraeutigam（2005）419ページ。
  13. ^サミュエルソン、Wとマークス、S（2003）。230ページ。
  14. ^サミュエルソン、Wとマークス、S（2003）。23ページ。
  15. ^ a b Pittman, Russell W. (2007年12月17日). 「反トラスト法執行における適切な基準としての消費者余剰」 . eLibraryで検索. SSRN 1075463. 2024年8月24日閲覧。 
  16. ^ Cheng, Ho Fung Griffith (2020年9月1日). 「略奪的価格設定の固有の妥当性と頻度に関する経済的視点：より積極的な規制の必要性」. European Competition Journal . 16 ( 2–3 ): 343–367 . doi : 10.1080/17441056.2020.1770478 . ISSN 1744-1056 . 

参考文献

  • ランズバーグ、S. (2002).価格理論とその応用（第5版）. サウスウェスタン.
  • リプシー、リチャード・G. (1975). 『実証経済学入門』（第4版）. ワイデンフェルド・ニコルソン. pp.  214–7 . ISBN 0-297-76899-9。
  • サミュエルソン, W.; マークス, S. (2003). 『マネジメント経済学』（第4版）. Wiley. ISBN 0470000449。
「 https://en.wikipedia.org/w/index.php?title=Profit_maximization&oldid=1329004043」より取得