Rectified tesseract
| Rectified tesseract | ||
|---|---|---|
 Schlegel diagramCentered on cuboctahedrontetrahedral cells shown | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | r{4,3,3} = 2r{3,31,1}h3{4,3,3} | |
| Coxeter-Dynkin diagrams |        =  | |
| Cells | 24 | 8 (3.4.3.4) 16 (3.3.3) |
| Faces | 88 | 64 {3}24 {4} |
| Edges | 96 | |
| Vertices | 32 | |
| Vertex figure | 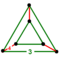 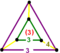 (Elongated equilateral-triangular prism) | |
| Symmetry group | B4 [3,3,4], order 384D4 [31,1,1], order 192 | |
| Properties | convex, edge-transitive | |
| Uniform index | 10 11 12 | |
In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope (4-dimensional polytope) bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract.
It has two uniform constructions, as a rectified 8-cell r{4,3,3} and a cantellated demitesseract, rr{3,31,1}, the second alternating with two types of tetrahedral cells.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC8.
Construction
The rectified tesseract may be constructed from the tesseract by truncating its vertices at the midpoints of its edges.
The Cartesian coordinates of the vertices of the rectified tesseract with edge length 2 is given by all permutations of:
Images
| Coxeter plane | B4 | B3 / D4 / A2 | B2 / D3 |
|---|---|---|---|
| Graph |  |  |  |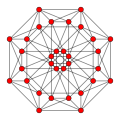
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | F4 | A3 | |
| Graph |  |  | |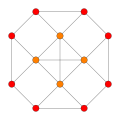
| Dihedral symmetry | [12/3] | [4] |
 Wireframe |  16 tetrahedral cells |
Projections
In the cuboctahedron-first parallel projection of the rectified tesseract into 3-dimensional space, the image has the following layout:
- The projection envelope is a cube.
- A cuboctahedron is inscribed in this cube, with its vertices lying at the midpoint of the cube's edges. The cuboctahedron is the image of two of the cuboctahedral cells.
- The remaining 6 cuboctahedral cells are projected to the square faces of the cube.
- The 8 tetrahedral volumes lying at the triangular faces of the central cuboctahedron are the images of the 16 tetrahedral cells, two cells to each image.
Alternative names
- Rit (Jonathan Bowers: for rectified tesseract)
- Ambotesseract (Neil Sloane & John Horton Conway)
- Rectified tesseract/Runcic tesseract (Norman W. Johnson)
- Runcic 4-hypercube/8-cell/octachoron/4-measure polytope/4-regular orthotope
- Rectified 4-hypercube/8-cell/octachoron/4-measure polytope/4-regular orthotope
Related uniform polytopes
Runcic cubic polytopes
| Runcic n-cubes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 4 | 5 | 6 | 7 | 8 | ||||||
| [1+,4,3n-2]= [3,3n-3,1] | [1+,4,32]= [3,31,1] | [1+,4,33]= [3,32,1] | [1+,4,34]= [3,33,1] | [1+,4,35]= [3,34,1] | [1+,4,36]= [3,35,1] | ||||||
| Runcicfigure | |  |  |  |  | ||||||
| Coxeter |  = | = | = | = | = | ||||||
| Schläfli | h3{4,32} | h3{4,33} | h3{4,34} | h3{4,35} | h3{4,36} | ||||||
Tesseract polytopes
| B4 symmetry polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | tesseract | rectifiedtesseract | truncatedtesseract | cantellatedtesseract | runcinatedtesseract | bitruncatedtesseract | cantitruncatedtesseract | runcitruncatedtesseract | omnitruncatedtesseract | ||
| Coxeterdiagram | | = | | | | = | | | | ||
| Schläflisymbol | {4,3,3} | t1{4,3,3}r{4,3,3} | t0,1{4,3,3}t{4,3,3} | t0,2{4,3,3}rr{4,3,3} | t0,3{4,3,3} | t1,2{4,3,3}2t{4,3,3} | t0,1,2{4,3,3}tr{4,3,3} | t0,1,3{4,3,3} | t0,1,2,3{4,3,3} | ||
| Schlegeldiagram |  | |  |  |  |  |  |  |  | ||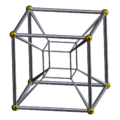
| B4 |  | |  |  |  |  |  |  |  | ||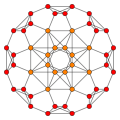
| Name | 16-cell | rectified16-cell | truncated16-cell | cantellated16-cell | runcinated16-cell | bitruncated16-cell | cantitruncated16-cell | runcitruncated16-cell | omnitruncated16-cell | ||
| Coxeterdiagram | =  | = | = | = | | = | = | | | ||
| Schläflisymbol | {3,3,4} | t1{3,3,4}r{3,3,4} | t0,1{3,3,4}t{3,3,4} | t0,2{3,3,4}rr{3,3,4} | t0,3{3,3,4} | t1,2{3,3,4}2t{3,3,4} | t0,1,2{3,3,4}tr{3,3,4} | t0,1,3{3,3,4} | t0,1,2,3{3,3,4} | ||
| Schlegeldiagram |  |  |  |  |  |  |  |  |  | ||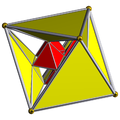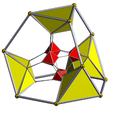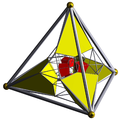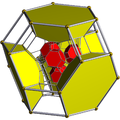
| B4 |  |  |  |  | | |  |  | | ||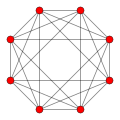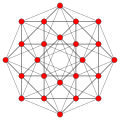
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6[1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman JohnsonUniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 11, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) o4x3o3o - rit".
