シンプソンの法則

シンプソンの法則の近似が、より多くの細分化によってどのように改善されるかを示すアニメーション。

数値積分において、シンプソンの規則は定積分のいくつかの近似であり、トーマス・シンプソン(1710–1761) にちなんで名付けられました。

これらのルールの中で最も基本的なものは、シンプソンの1/3ルール、または単にシンプソンのルールと呼ばれ、 $\int _{a}^{b}f(x)\,dx\approx {\frac {ba}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right].$

ドイツ語をはじめとするいくつかの言語では、ヨハネス・ケプラーにちなんで名付けられています。ケプラーは1615年にワイン樽の法則（樽則、 Keplersche Fassregel ）を見てこの法則を導き出しました。この法則の近似等式は、 $f$ が3次までの多項式である場合に正確になります。

1/3則を積分範囲[ a , b ]のn等分部分に適用すると、合成シンプソンの1/3則が得られる。積分範囲内の点には、交互に4/3と2/3の重みが与えられる。

シンプソンの 3/8 則(シンプソンの第 2 則とも呼ばれる) では、積分範囲内でもう 1 つの関数評価が必要となり、誤差範囲は低くなりますが、誤差の順序は改善されません。

3/8規則を積分範囲[ a、 b ]のn個の等しい分割に適用すると、合成シンプソンの3/8規則が得られます。

シンプソンの 1/3 規則と 3/8 規則は、閉じたニュートン-コーツの公式の 2 つの特殊なケースです。

造船学や船舶の安定性評価においても、シンプソンの第3法則が存在します。これは一般的な数値解析では特別な重要性を持ちません。シンプソンの法則（船舶の安定性）を参照してください。

シンプソンの1/3則

シンプソンの1/3則は、単にシンプソン則とも呼ばれ、トーマス・シンプソンによって提唱された数値積分の方法です。これは二次補間に基づいており、について評価された合成シンプソンの1/3則です。シンプソンの1/3則は次のとおりです。はの刻み幅です $n=2$ ${\begin{aligned}\int _{a}^{b}f(x)\,dx&\approx {\frac {ba}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right]\\&={\frac {1}{3}}h\left[f(a)+4f\left(a+h\right)+f(b)\right],\end{aligned}}$ $h=(ba)/n$ $n=2$

シンプソンの定理による積分の近似誤差は、（ギリシャ文字のxi ）がとの間のある数であるときである。^[¹^]^[²^] $n=2$ $-{\frac {1}{90}}h^{5}f^{(4)}(\xi )=-{\frac {(ba)^{5}}{2880}}f^{(4)}(\xi ),$ $\xi$ $a$ $b$

誤差は漸近的にに比例します。しかし、上記の導出は誤差がに比例することを示唆しています。シンプソン則は、積分関数が評価される点が区間内で対称的に分布しているため、さらに次の次数を得ます。 $(ba)^{5}$ $(ba)^{4}$ $[a,\ b]$

誤差項はにおけるの4次導関数に比例するため、シンプソンの定理は3次以下の任意の多項式に対して正確な結果を与えることを示しています。なぜなら、そのような多項式の4次導関数はすべての点でゼロになるからです。この結果を別の方法で理解するには、任意の補間3次多項式は、唯一の補間2次多項式と、区間内の3点すべてでゼロになる任意にスケールされた3次多項式との和として表すことができ、この2番目の項の積分は区間内で奇数であるためゼロになることに注目してください。 $f$ $\xi$ $f$

2次導関数が存在し、区間内で凸である場合、 $f''$ $(a,\ b)$ $(ba)f\left({\frac {a+b}{2}}\right)+{\frac {1}{3}}\left({\frac {ba}{2}}\right)^{3}f''\left({\frac {a+b}{2}}\right)\leq \int _{a}^{b}f(x)\,dx\leq {\frac {ba}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right].$

導出

二次補間

との間の一般放物線の面積を、ある正の数に対して求めることを考えてみましょう。したがって、この区間の中点はです $y=ax^{2}+bx+c$ $x=-h$ $x=h$ $h$ $x=0$

したがって、放物線の下の面積は $A$

${\begin{aligned}A=\int _{-h}^{h}ax^{2}+bx+c\,dx&=\left[{\frac {ax^{3}}{3}}+{\frac {bx^{2}}{2}}+cx\right]_{x=-h}^{x=h}\\&=\left({\frac {ah^{3}}{3}}+{\frac {bh^{2}}{2}}+ch\right)-\left(-{\frac {ah^{3}}{3}}+{\frac {bh^{2}}{2}}-ch\right)\\&={\frac {2ah^{3}}{3}}+2ch\\&={\frac {h}{3}}\left(2ah^{2}+6c\right).\end{aligned}}$

放物線に中点と端点があり、これら3点を放物線の公式に代入すると次のようになる。 $(0,y_{1})$ $(-h,y_{0})$ $(h,y_{2})$

$y_{0}=ah^{2}-bh+c$ $y_{1}=c$ $y_{2}=ah^{2}+bh+c$

これらを解くと

$c=y_{1}$

2番目の方程式から、そして

$2ah^{2}=y_{0}-2y_{1}+y_{2}$

1番目と3番目の方程式を足し合わせると。これをの式に代入すると、 $A$

${\begin{aligned}A&={\frac {h}{3}}\left(2ah^{2}+6c\right)\\&={\frac {h}{3}}\left(y_{0}-2y_{1}+y_{2}+6y_{1}\right)\\&={\frac {h}{3}}\left(y_{0}+4y_{1}+y_{2}\right).\end{aligned}}$

シンプソンの1/3則は、区間 $[a, b]$ 上の定積分を、積分関数を放物線で置き換えて近似し、その放物線は区間の中点で関数を補間する。 $x=a$ $x=b$

$\int _{a}^{b}f(x)\,dx\approx A={\frac {1}{3}}h\left[f(a)+4f(a+h)+f(b)\right].$ この係数のため、シンプソンの法則は「シンプソンの 1/3 法則」とも呼ばれます (一般化については以下を参照)。 $1/3$

中点の平均化と台形則

別の導出では、2つのより単純な近似からシンプソン則を構築します。区間上で多項式のように振舞う関数について、中点則はとなり、台形則はとなります。ここではに漸近的に比例する項を表します。2つの項は等しくありません。詳細はBig O記法を参照してください。上記の式から、加重平均を取ると、先頭の誤差項が消えることが分かります。この加重平均はまさにシンプソン則です。 $[a,b]$ $M=(ba)f\left({\frac {a+b}{2}}\right)=\int _{a}^{b}f(x)dx-{\frac {1}{24}}(ba)^{3}f''(a)+O{\big (}(ba)^{4}{\big )}$ $T=(ba)\left({\frac {f(a)+f(b)}{2}}\right)=\int _{a}^{b}f(x)dx+{\frac {1}{12}}(ba)^{3}f''(a)+O{\big (}(ba)^{4}{\big )},$ $O{\big (}(ba)^{4}{\big )}$ $(ba)^{4}$ $O{\big (}(ba)^{4}{\big )}$ ${\frac {2M+T}{3}}=\int _{a}^{b}f(x)\,dx+O((ba)^{4}).$

別の近似法（例えば、点数が2倍の台形則）を用いることで、適切な加重平均を取り、別の誤差項を除去することが可能です。これがロンバーグ法です。

未定係数

3番目の導出は仮定から始まります ${\frac {1}{ba}}\int _{a}^{b}f(x)\,dx\approx \alpha f(a)+\beta f\left({\frac {a+b}{2}}\right)+\gamma f(b).$

係数 $α$ 、 $β$ 、 $γ は、$ この近似がすべての二次多項式に対して正確であることを要求することで固定できます。これによりシンプソンの定理が得られます。（この導出は本質的に二次補間導出の厳密さを少し緩めたもので、正しい関数形を推測することで計算量を大幅に節約できます。）

複合シンプソンの1/3ルール

積分区間が何らかの意味で「小さい」場合、部分区間を用いたシンプソンの定理は、正確な積分を適切に近似します。「小さい」とは、積分される関数が区間にわたって比較的滑らかであることを意味します。このような関数の場合、シンプソンの定理で使用されるような滑らかな二次補間関数は良好な結果をもたらします。 $[a,b]$ $n=2$ $[a,b]$

しかし、積分しようとしている関数が区間全体にわたって滑らかでないことはよくあります。典型的には、関数が強く振動しているか、特定の点で導関数が欠落していることを意味します。このような場合、シンプソンの法則は非常に悪い結果をもたらす可能性があります。この問題に対処する一般的な方法の一つは、区間を小さな部分区間に分割することです。そして、各部分区間にシンプソンの法則を適用し、その結果を合計することで、区間全体の積分の近似値を生成します。このようなアプローチは、複合シンプソンの1/3法則、または単に複合シンプソンの法則と呼ばれます。 $[a,b]$ $n>2$

区間が偶数個の部分区間に分割されていると仮定する。この場合、合成シンプソン則は次のように与えられる。 $[a,b]$ $n$ $n$

区間を長さのサブ区間に分割し、（特に、および）の点を導入すると、次の式が得られます。を伴うこの合成規則は、前のセクションの通常のシンプソンの規則に対応します。 $[a,b]$ $n$ $h=(ba)/n$ $x_{i}=a+ih$ $0\leq i\leq n$ $x_{0}=a$ $x_{n}=b$ ${\begin{aligned}\int _{a}^{b}f(x)\,dx&\approx {\frac {1}{3}}h\sum _{i=1}^{n/2}{\big [}f(x_{2i-2})+4f(x_{2i-1})+f(x_{2i}){\big ]}\\&={\frac {1}{3}}h{\big [}f(x_{0})+4f(x_{1})+2f(x_{2})+4f(x_{3})+2f(x_{4})+\dots +2f(x_{n-2})+4f(x_{n-1})+f(x_{n}){\big ]}\\&={\frac {1}{3}}h\left[f(x_{0})+4\sum _{i=1}^{n/2}f(x_{2i-1})+2\sum _{i=1}^{n/2-1}f(x_{2i})+f(x_{n})\right].\end{aligned}}$ $n=2$

合成シンプソン則によって生じる誤差は、との間の任意の数値であり、は「ステップ長」である。^[³^]^[⁴^]誤差は（絶対値で）で制限される。 $-{\frac {1}{180}}h^{4}(b-a)f^{(4)}(\xi ),$ $\xi$ $a$ $b$ $h=(b-a)/n$ ${\frac {1}{180}}h^{4}(b-a)\max _{\xi \in [a,b]}\left|f^{(4)}(\xi )\right|.$

この定式化は、区間を等しい長さの部分区間に分割します。実際には、異なる長さの部分区間を用いて、積分関数の挙動があまり良くない箇所に集中的に計算を行うことが有利な場合が多くあります。これが適応型シンプソン法です。 $[a,b]$

例

2の自然対数の近似

なので

$\int _{1}^{2}{\frac {1}{x}}\,dx=\ln(2)-\ln(1)=\ln(2),$

この積分を近似することで、の近似値を生成することができます。区間に合成シンプソンの1/3則を適用すると、次のようになります $\ln(2)$ $n=6$ ${\begin{aligned}\ln(2)=\int _{1}^{2}{\frac {1}{x}}\,dx&\approx {\frac {1}{18}}\left(\ 1+{\frac {24}{7}}+{\frac {3}{2}}+{\frac {8}{3}}+{\frac {6}{5}}+{\frac {24}{11}}+{\frac {1}{2}}\right)\\&\approx 0.69316,\end{aligned}}$

相対誤差は約です。 $0.003\%$

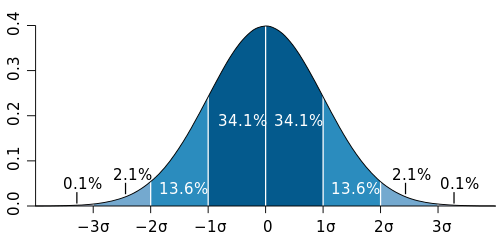
統計への応用

統計学では、データが左右に偏りなく中心値付近に分布する場合、正規分布に従うと言われます。平均が0で標準偏差が1の場合、曲線は標準正規分布（または標準ガウス分布）に従うと言われます。^{[ 5 ]}この分布の式は

$f(x)={\frac {1}{\sqrt {2\pi }}}\exp \left({\frac {-x^{2}}{2}}\right).$

68-95-99.7ルールによれば、値の約68.27%が平均値の1標準偏差以内にあるため、

$\int _{-1}^{1}{\frac {1}{\sqrt {2\pi }}}{\dot {\exp }}\left({\frac {-x^{2}}{2}}\right)dx\approx 0.6827.$

この結果は、複合シンプソンの1/3ルールで検証できます。このルールを区間に適用すると、 $n=6$ ${\begin{aligned}\int _{-1}^{1}{\frac {1}{\sqrt {2\pi }}}\exp \left({\frac {-x^{2}}{2}}\right)\,dx&\approx {\frac {1}{\sqrt {2\pi }}}\times {\frac {1}{9}}\left(\ {\frac {1}{e^{\frac {1}{2}}}}+{\frac {4}{e^{\frac {2}{9}}}}+{\frac {2}{e^{\frac {1}{18}}}}+{\frac {4}{1}}+{\frac {2}{e^{\frac {1}{18}}}}+{\frac {4}{e^{\frac {2}{9}}}}+{\frac {1}{e^{\frac {1}{2}}}}\right)\\&\approx {\frac {1}{\sqrt {2\pi }}}\times 1.71142\\&\approx 0.6827,\end{aligned}}$

予想通りです。

同様に、68-95-99.7のルールでは、値の約95.45%が平均値の2標準偏差以内にあるとされています。つまり

$\int _{-2}^{2}{\frac {1}{\sqrt {2\pi }}}{\dot {\exp }}\left({\frac {-x^{2}}{2}}\right)dx\approx 0.9545.$

以前と同様に、この結果は複合シンプソンの1/3ルールで検証できます。このルールを区間に適用すると、 $n=6$ ${\begin{aligned}\int _{-2}^{2}{\frac {1}{\sqrt {2\pi }}}\exp \left({\frac {-x^{2}}{2}}\right)\,dx&\approx {\frac {1}{\sqrt {2\pi }}}\times {\frac {2}{9}}\left(\ {\frac {1}{e^{2}}}+{\frac {4}{e^{\frac {8}{9}}}}+{\frac {2}{e^{\frac {2}{9}}}}+{\frac {4}{1}}+{\frac {2}{e^{\frac {2}{9}}}}+{\frac {4}{e^{\frac {8}{9}}}}+{\frac {1}{e^{2}}}\right)\\&\approx {\frac {1}{\sqrt {2\pi }}}\times 2.39167\\&\approx 0.9541,\end{aligned}}$

これは約の相対誤差を持つ。積分区間は、被積分関数が偶関数であることに留意することで短縮できる（したがって離散化誤差が減少する）。 $0.0419\%$

$\int _{-2}^{2}{\frac {1}{\sqrt {2\pi }}}\exp \left({\frac {-x^{2}}{2}}\right)\,dx=2\int _{0}^{2}{\frac {1}{\sqrt {2\pi }}}\exp \left({\frac {-x^{2}}{2}}\right)\,dx.$

もう一度、シンプソンの1/3の合成則を区間に適用すると、 $n=6$ ${\begin{aligned}2\int _{0}^{2}{\frac {1}{\sqrt {2\pi }}}\exp \left({\frac {-x^{2}}{2}}\right)\,dx&\approx {\frac {2}{\sqrt {2\pi }}}\times {\frac {1}{9}}\left(\ 1+{\frac {4}{e^{\frac {1}{18}}}}+{\frac {2}{e^{\frac {2}{9}}}}+{\frac {4}{e^{\frac {1}{2}}}}+{\frac {2}{e^{\frac {8}{9}}}}+{\frac {4}{e^{\frac {25}{18}}}}+{\frac {1}{e^{2}}}\right)\\&\approx {\frac {2}{\sqrt {2\pi }}}\times 1.19626\\&\approx 0.9544,\end{aligned}}$

相対誤差は約に改善されていますが、間隔の数は同じです。 $0.0104\%$

$π$ の近似

なので

$\int _{0}^{1}{\frac {1}{1+x^{2}}}\,dx=\arctan(1)-\arctan(0)={\frac {\pi }{4}},$

これを並べ替えると

$\pi =4\int _{0}^{1}{\frac {1}{1+x^{2}}}\,dx.$

したがって、この積分を近似することでの近似値を生成することができる。区間に合成シンプソンの1/3則を適用すると、次のようになる。 $\pi$ $n=6$ ${\begin{aligned}\pi =4\int _{0}^{1}{\frac {1}{1+x^{2}}}\,dx&\approx {\frac {2}{9}}\left(\ 1+{\frac {144}{37}}+{\frac {9}{5}}+{\frac {16}{5}}+{\frac {18}{13}}+{\frac {144}{61}}+{\frac {1}{2}}\right)\\&\approx 3.141591,\end{aligned}}$

驚くべきことに、相対誤差は約しかありません。 $0.00002\%$

望ましい精度を得るための間隔の数を決定する

絶対誤差が未満となる近似に必要な区間の数を決定したいとします。複合シンプソンの1/3則における誤差項は $\int _{0}^{\pi }\sin(x)\,dx$ $0.00001$

$-{\frac {\pi h^{4}}{180}}\sin(\xi )$

との間の値を求める。絶対誤差はより小さいので、次のように計算できる。 $\xi$ $0$ $\pi$ $0.00001$

$\left|{\frac {\pi h^{4}}{180}}\sin(\xi )\right|\leq {\frac {\pi h^{4}}{180}}={\frac {\pi ^{5}}{180n^{4}}}<0.00001$

となる

$n>{\sqrt[{4}]{\frac {\pi ^{5}}{0.0018}}}\approx 20.3,$

必要な精度が得られます。 $n=22$

比較のために、合成台形則を用いてこの程度の精度を確保したいとします。この場合、誤差項は

$-{\frac {\pi h^{2}}{12}}\sin(\xi )$

との間の値を求める。絶対誤差はより小さいので、次のように計算できる。 $\xi$ $0$ $\pi$ $0.00001$

$\left|{\frac {\pi h^{2}}{12}}\sin(\xi )\right|\leq {\frac {\pi h^{2}}{12}}={\frac {\pi ^{3}}{12n^{2}}}<0.00001$

となる

$n>{\sqrt {\frac {\pi ^{3}}{0.00012}}}\approx 508.3,$

必要な精度を保証します。これは、複合シンプソンの1/3ルールと比較して、大幅に多くの計算を必要とします。 $n=509$

シンプソンの3/8則

シンプソンの3/8則は、シンプソンの第二則とも呼ばれ、トーマス・シンプソンによって提唱された数値積分のもう一つの方法です。これは、二次補間ではなく三次補間に基づいています

との間の一般立方体の下で、ある正の数に対して面積を求めることを考えてみましょう。これは次のように与えられます。 $A$ $y=ax^{3}+bx^{2}+cx+d$ $x=-h$ $x=2h$ $h$

${\begin{aligned}A&=\int _{-h}^{2h}\left(ax^{3}+bx^{2}+cx+d\right)\,dx\\[1ex]&=\left[{\frac {1}{4}}ax^{4}+{\frac {1}{3}}bx^{3}+{\frac {1}{2}}cx^{2}+dx\right]_{x=-h}^{x=2h}\\[1ex]&=\left(4ah^{4}+{\frac {8}{3}}bh^{3}+2ch^{2}+2dh\right)-\left({\frac {1}{4}}ah^{4}-{\frac {1}{3}}bh^{3}+{\frac {1}{2}}ch^{2}-dh\right)\\[1ex]&={\frac {15}{4}}ah^{4}+3bh^{3}+{\frac {3}{2}}ch^{2}+3dh\\[1ex]&={\frac {3h}{8}}\left[10ah^{3}+8bh^{2}+4ch+8d\right].\end{aligned}}$

積分区間上の等間隔の4点を、、およびと仮定し、これらの4点を3次方程式の公式に代入すると、 $(-h,y_{0})$ $(0,y_{1})$ $(h,y_{2})$ $(2h,y_{3})$

$y_{0}=-ah^{3}+bh^{2}-ch+d$ $y_{1}=d$ $y_{2}=ah^{3}+bh^{2}+ch+d$ $y_{3}=8ah^{3}+4bh^{2}+2ch+d.$

最初の式と3番目の式を加えると

$y_{0}+y_{2}=2bh^{2}+2d$

そして、4番目の式を2番目の式に2倍して加えると、

$y_{3}+2y_{2}=10ah^{3}+6bh^{2}+4ch+3d.$

これで

${\begin{aligned}A&={\frac {3h}{8}}\left[10ah^{3}+8bh^{2}+4ch+8d\right]\\&={\frac {3h}{8}}\left[\underbrace {10ah^{3}+6bh^{2}+4ch+3d} _{y_{3}+2y_{2}}+\underbrace {2bh^{2}+2d} _{y_{0}+y_{2}}+3\underbrace {d} _{y_{1}}\right]\\&={\frac {3h}{8}}\left[y_{0}+3y_{1}+3y_{2}+y_{3}\right].\end{aligned}}$

シンプソンの3/8則は、区間 $[a, b]$ 上の定積分を、積分関数を等間隔の4点、、、で補間する3次関数に置き換えることで近似します。ここで、は刻み幅です。これは以下のようになります $x=a$ $x=a+h$ $x=a+2h$ $x=a+3h=b$ $h={\frac {b-a}{3}}$

${\begin{aligned}\int _{a}^{b}f(x)\,dx\approx A&={\frac {3}{8}}h\left[f(a)+3f\left(a+h\right)+3f\left(a+2h\right)+f(b)\right].\end{aligned}}$

この方法の誤差はであり、はとの間の任意の数値です。したがって、3/8ルールは標準的な方法の約2倍の精度ですが、関数の値が1つ多く使用されます。上記と同様に、複合3/8ルールも存在します。^[⁶^] $-{\frac {3}{80}}h^{5}f^{(4)}(\xi )=-{\frac {(b-a)^{5}}{6480}}f^{(4)}(\xi ),$ $\xi$ $a$ $b$

任意次数多項式による補間に対するこの概念のさらなる一般化は、ニュートン・コーツの公式です。

複合シンプソンの3/8ルール

区間を長さの部分区間に分割し、（特に、および）の点を導入すると、 $[a,b]$ $n$ $h=(b-a)/n$ $x_{i}=a+ih$ $0\leq i\leq n$ $x_{0}=a$ $x_{n}=b$ ${\begin{aligned}\int _{a}^{b}f(x)\,dx&\approx {\frac {3}{8}}h\sum _{i=1}^{n/3}{\big [}f(x_{3i-3})+3f(x_{3i-2})+3f(x_{3i-1})+f(x_{3i}){\big ]}\\&={\frac {3}{8}}h{\big [}f(x_{0})+3f(x_{1})+3f(x_{2})+2f(x_{3})+3f(x_{4})+3f(x_{5})+2f(x_{6})+\dots \\&\qquad +2f(x_{n-3})+3f(x_{n-2})+3f(x_{n-1})+f(x_{n}){\big ]}\\&={\frac {3}{8}}h\left[f(x_{0})+3\sum _{i=1,\ 3\nmid i}^{n-1}f(x_{i})+2\sum _{i=1}^{n/3-1}f(x_{3i})+f(x_{n})\right].\end{aligned}}$

この規則の剰余は^{[ 6 ]} で示されていますが、これはが3の倍数の場合にのみ使用できます。1/3規則は、誤差項の順序を変えることなく、残りの部分区間に適用できます（逆に、奇数部分区間では、3/8規則を合成1/3規則と組み合わせて使用できます）。 $-{\frac {1}{80}}h^{4}(b-a)f^{(4)}(\xi ),$ $n$

数値例

正弦曲線の半周期にわたる弧長を計算したいとします。弧長の公式を用いると、次のように表すことができます $L$ $y=\sin(x)$

$L=\int _{0}^{\pi }{\sqrt {1+(y')^{2}}}\,dx=\int _{0}^{\pi }{\sqrt {1+[\cos(x)]^{2}}}\,dx$

これは非基本積分ですが、と示すこともできます。ここではレムニスケート定数です。 ${\frac {\pi }{\varpi }}+\varpi \approx 3.820197789$ $\varpi$

シンプソンの3/8ルールを間隔付きで適用すると、 $n=6$

${\begin{aligned}L=\int _{0}^{\pi }{\sqrt {1+[\cos(x)]^{2}}}\,dx&\approx {\frac {\pi }{16}}{\dot {\left(\ {\sqrt {2}}+{\frac {3{\sqrt {7}}}{2}}+{\frac {3{\sqrt {5}}}{2}}+2+{\frac {3{\sqrt {5}}}{2}}+{\frac {3{\sqrt {7}}}{2}}+{\sqrt {2}}\right)}}\\&={\frac {\pi }{16}}\left(2{\sqrt {2}}+3{\sqrt {7}}+3{\sqrt {5}}+2\right)\\&\approx 3.823688376,\end{aligned}}$

相対誤差はわずかと良好です。 $0.0913\%$

代替拡張シンプソン則

これは合成シンプソン則の別の定式化である。近似する積分の互いに素な部分にシンプソン則を適用する代わりに、重なり合う部分にシンプソン則を適用し、^{[ 7 ]を得る。}

${\begin{aligned}\int _{a}^{b}f(x)\,dx\approx {\frac {1}{48}}h{\bigg [}&17f(x_{0})+59f(x_{1})+43f(x_{2})+49f(x_{3})\\+&48\sum _{i=4}^{n-4}f(x_{i})\\+&49f(x_{n-3})+43f(x_{n-2})+59f(x_{n-1})+17f(x_{n}){\bigg ]}\end{aligned}}$ 上記の式は、シンプソンの1/3法則と、端の部分区間ではシンプソンの3/8法則、残りの部分区間ではシンプソンの1/3法則を適用した法則を組み合わせることで得られます。そして、2つの式の平均をとることで結果が得られます。

狭いピークの場合のシンプソンの法則

狭いピーク状関数の全領域を推定するタスクでは、シンプソンの規則は台形規則よりもはるかに効率が悪い。つまり、合成シンプソンの 1/3 規則では、台形規則と同じ精度を得るために 1.8 倍の点が必要である。^{[ 8 ]}合成シンプソンの 3/8 規則はさらに精度が悪い。シンプソンの 1/3 規則による積分は、ステップhの台形規則による積分から得られる値の 2/3 と、ステップ 2 hの長方形規則による積分から得られる値の 1/3 を使用した加重平均として表すことができる。精度は 2 番目の (2 hステップ) 項によって決まる。適切にシフトされたフレームを持つシンプソンの 1/3 規則の合成和を平均すると、次の規則が得られる: 積分領域外の 2 つの点が利用され、積分領域内の点のみ使用される。 2 番目のルールを 3 点の領域に適用すると、1/3 シンプソンルールが生成され、4 点では 3/8 ルールが生成されます。 $\int _{a}^{b}f(x)\,dx\approx {\frac {1}{24}}h\left[-f(x_{-1})+12f(x_{0})+25f(x_{1})+24\sum _{i=2}^{n-2}f(x_{i})+25f(x_{n-1})+12f(x_{n})-f(x_{n+1})\right],$ $\int _{a}^{b}f(x)\,dx\approx {\frac {1}{24}}h\left[9f(x_{0})+28f(x_{1})+23f(x_{2})+24\sum _{i=3}^{n-3}f(x_{i})+23f(x_{n-2})+28f(x_{n-1})+9f(x_{n})\right],$

これらの規則は代替拡張シンプソン則に非常によく似ている。積分される領域の大部分内の係数は、端にのみ非単位係数を持つ 1 である。これら 2 つの規則は、1 次導関数項を持つオイラー・マクローリンの公式に関連し、 1 次オイラー・マクローリン積分則と呼ばれる。^{[ 8 ]}上記の 2 つの規則は、領域端での 1 次導関数の計算方法のみが異なっている。オイラー・マクローリン積分則における 1 次導関数項は、2 次導関数の積分を表し、これは積分領域の端での 1 次導関数の差に等しい。オイラー・マクローリンの公式で定義されるように、係数を持つ 3 次、5 次、… の導関数の差を追加することで、より高次のオイラー・マクローリン則を生成することが可能である。

不規則な間隔のデータに対する複合シンプソンの法則

いくつかの応用では、積分区間を不均等な区間に分割する必要がある場合があります。これは、データの不均等なサンプリング、あるいはデータ点の欠損や破損などが原因である可能性があります。区間を幅の偶数個の部分区間に分割するとします。この場合、合成シンプソン則は^[⁹^]で与えられます。ここで、は区間上の番目のサンプリング点における関数値です。 $I=[a,b]$ $I$ $N$ $h_{k}$ $\int _{a}^{b}f(x)\,dx\approx \sum _{i=0}^{N/2-1}{\frac {h_{2i}+h_{2i+1}}{6}}\left[\left(2-{\frac {h_{2i+1}}{h_{2i}}}\right)f_{2i}+{\frac {(h_{2i}+h_{2i+1})^{2}}{h_{2i}h_{2i+1}}}f_{2i+1}+\left(2-{\frac {h_{2i}}{h_{2i+1}}}\right)f_{2i+2}\right],$ $f_{k}=f\left(a+\sum _{i=0}^{k-1}h_{i}\right)$ $k$ $I$

区間の数が奇数 $N$ の場合、上記の式は最後から2番目の区間まで適用され、最後の区間は結果に次の式を加算して個別に処理されます。^{[ 10 ]} $\alpha f_{N}+\beta f_{N-1}-\eta f_{N-2},$ ${\begin{aligned}\alpha &={\frac {2h_{N-1}^{2}+3h_{N-1}h_{N-2}}{6(h_{N-2}+h_{N-1})}},\\[1ex]\beta &={\frac {h_{N-1}^{2}+3h_{N-1}h_{N-2}}{6h_{N-2}}},\\[1ex]\eta &={\frac {h_{N-1}^{3}}{6h_{N-2}(h_{N-2}+h_{N-1})}}.\end{aligned}}$

Pythonでの実装例

collections.abcからシーケンスをインポートdef simpson_nonuniform ( x : Sequence [ float ], f : Sequence [ float ]) -> float : """ 不規則に間隔が空いたデータに対するシンプソン規則。 :param x: 関数値のサンプリング点 :param f: サンプリング点における関数値 :return: 積分の近似値 numpyのブロードキャストを利用したよりパフォーマンスの高い実装については、 ``scipy.integrate.simpson``とその基礎となる``_basic_simpson``を参照してください。  """ N = len ( x ) - 1 h = [ x [ i + 1 ] - x [ i ] for i in range ( 0 , N )] assert N > 0範囲( 1 , N , 2 )内のiの場合、結果= 0.0 になります。 h0 、h1 = h [ i - 1 ]、h [ i ] hph 、hdh 、hmh = h1 + h0 、h1 / h0 、h1 * h0結果+= ( hph / 6 ) * ( ( 2 - hdh ) * f [ i - 1 ] + ( hph ** 2 / hmh ) * f [ i ] + ( 2 - 1 / hdh ) * f [ i + 1 ] )N % 2 == 1 の場合: h0 、h1 = h [ N - 2 ]、h [ N - 1 ]結果+= f [ N ] * ( 2 * h1 ** 2 + 3 * h0 * h1 ) / ( 6 * ( h0 + h1 ))結果+= f [ N - 1 ] * ( h1 ** 2 + 3 * h1 * h0 ) / ( 6 * h0 )結果-= f [ N - 2 ] * h1 ** 3 / ( 6 * h0 * ( h0 + h1 ))結果を返す

Rでの実装例

SimpsonInt <- function ( fx , dx ) { n <- length ( dx ) h <- diff ( dx ) stopifnot ( exprs = { length ( fx ) == n all ( h >= 0 ) }) res <- 0 for ( i in seq ( 1L , n - 2L , 2L )) { hph <- h [ i ] + h [ i + 1L ] hdh <- h [ i + 1L ] / h [ i ] res <- res + hph / 6 * (( 2 - hdh ) * fx [ i ] + hph ^ 2 / ( h [ i ] * h [ i + 1L ]) * fx [ i + 1L ] + ( 2 - 1 / hdh ) * fx [ i + 2L ]) }もしn %% 2 == 0なら{ hph <- h [ n - 1L ] + h [ n - 2L ] threehth < - 3 * h [ n - 1L ] * h [ n - 2L ] sixh2 <- 6 * h [ n - 2L ] h1sq <- h [ n - 1L ] ^ 2 res <- res + ( 2 * h1sq + threehth ) / ( 6 * hph ) * fx [ n ] + ( h1sq + threehth ) / sixh2 * fx [ n - 1L ] - ( h1sq * h [ n - 1L ]) / ( sixh2 * hph ) * fx [ n - 2L ] } res }

数値安定性

すべてのニュートン・コーツ公式に共通するシンプソン則の重要な性質は、丸め誤差に関する安定性です。説明のために、区間 $[a, b]$ 上の関数に部分区間を含む複合シンプソン則を適用するとします。が計算されたときの丸め誤差を、が複合シンプソン則における累積誤差の総和を表します。ここで $n$ $f(x)$ $e_{i}$ $f(x_{i})$ $E(h)$ $h={\frac {b-a}{n}}$

定義により、 ${\begin{aligned}E(h)&=\left|{\frac {h}{3}}\left[e_{0}+2\sum _{j=1}^{(n/2)-1}e_{2j}+4\sum _{j=1}^{n/2}e_{2j-1}+e_{n}\right]\right|\\&\leq {\frac {h}{3}}\left[\left|e_{0}\right|+2\sum _{j=1}^{(n/2)-1}\left|e_{2j}\right|+4\sum _{j=1}^{n/2}\left|e_{2j-1}\right|+\left|e_{n}\right|\right].\end{aligned}}$

丸め誤差がある数値で制限されると仮定すると、次のようになります $\varepsilon >0$

${\begin{aligned}E(h)&\leq {\frac {h}{3}}\left[\varepsilon +2\left({\frac {n}{2}}-1\right)\varepsilon +4\left({\frac {n}{2}}\right)\varepsilon +\varepsilon \right]\\&={\frac {h}{3}}3n\varepsilon \\[1ex]&=nh\varepsilon \\[1ex]&=n\left({\frac {b-a}{n}}\right)\varepsilon \\&=(b-a)\varepsilon ,\end{aligned}}$

これはに依存しない境界値であるため、がゼロに近づくにつれて手順は安定します。これは、条件が悪くなる数値微分法とは対照的です。 $h$ $h$

参照

注釈

^アトキンソン1989、式（5.1.15）。
^ Süli & Mayers 2003、§7.2。
^アトキンソン 1989、257–258ページ。
^ Süli & Mayers 2003、§7.5。
^ 「標準正規分布」 Scribbr。2020年11月5日。 2025年9月3日閲覧。
^ ^a ^bマシューズ 2004 .
^ Weisstein、式35。
^ ^a ^bカランベット、コズミン、サモヒン、2018 年。
^シュクロフ 1960 .
^ Cartwright 2017、式8。Cartwrightの式は最初の区間を計算しているのに対し、Wikipediaの記事の式は最後の積分を調整しています。適切な代数的置換が行われれば、式は示されている値になります。

参考文献

アトキンソン、ケンドール・E. (1989).数値解析入門（第2版）. John Wiley & Sons. ISBN 0-471-50023-2。
バーデン、リチャード・L.、フェアーズ、J.・ダグラス (2000).数値解析（第7版）. ブルックス/コール. ISBN 0-534-38216-9。
カートライト、ケネス・V. (2017年9月). 「MS Excelと不規則間隔データを用いたシンプソン則累積積分」(PDF) .数学科学・数学教育ジャーナル. 12 (2): 1–9 . 2022年12月18日閲覧
Kalambet, Yuri; Kozmin, Yuri; Samokhin, Andrey (2018). 「非常に狭いクロマトグラフィーピークの場合の積分則の比較」. Chemometrics and Intelligent Laboratory Systems . 179 : 22–30 . doi : 10.1016/j.chemolab.2018.06.001 . ISSN 0169-7439 .
マシューズ、ジョン・H. (2004). 「数値積分におけるシンプソンの3/8則」 .数値解析 - 数値手法プロジェクト. カリフォルニア州立大学フラートン校. 2008年12月4日時点のオリジナルよりアーカイブ。 2008年11月11日閲覧。
Shklov, N. (1960年12月). 「不等間隔の縦座標に対するシンプソンの定理」.アメリカ数学月刊誌. 67 (10): 1022–1023 . doi : 10.2307/2309244 . JSTOR 2309244 .
スーリ、エンドレ、メイヤーズ、デイヴィッド (2003). 『数値解析入門』ケンブリッジ大学出版局. ISBN 0-521-00794-1。
ワイススタイン、エリック・W. 「ニュートン・コーツの公式」 MathWorld . 2022年12月14日閲覧

外部リンク

「シンプソンの公式」数学百科事典EMSプレス2001[1994]。
ワイスタイン、エリック W. 「シンプソンの法則」。MathWorld 。
シンプソンの積分の1/3則 — ノート、PPT、Mathcad、Matlab、Mathematica、Maple（STEM学部生向け数値計算法）
コンピュータ実装の詳細な説明は、Dorai Sitaram著のFixnum Daysの付録C 「Teach Yourself Scheme」に記載されています。

この記事には、 Creative Commons Attribution-Share-Alike Licenseに基づいてライセンスされているPlanetMathの Code for Simpson's rule からの資料が組み込まれています。

[FOOTNOTEAtkinson1989equation_(5.1.15)-1] アトキンソン1989、式（5.1.15）。

[FOOTNOTESüliMayers2003§7.2-2] Süli & Mayers 2003、§7.2。

[FOOTNOTEAtkinson1989257–258-3] アトキンソン 1989、257–258ページ。

[FOOTNOTESüliMayers2003§7.5-4] Süli & Mayers 2003、§7.5。

[5] 「標準正規分布」 Scribbr。2020年11月5日。 2025年9月3日閲覧。

[FOOTNOTEMatthews2004-6] マシューズ 2004 .

[FOOTNOTEWeissteinEquation_35-7] Weisstein、式35。

[FOOTNOTEKalambetKozminSamokhin2018-8] カランベット、コズミン、サモヒン、2018 年。

[FOOTNOTEShklov1960-9] シュクロフ 1960 .

[FOOTNOTECartwright2017Equation_8._The_equation_in_Cartwright_is_calculating_the_first_interval_whereas_the_equations_in_the_Wikipedia_article_are_adjusting_for_the_'''last'''_integral._If_the_proper_algebraic_substitutions_are_made,_the_equation_results_in_the_values_shown-10] Cartwright 2017、式8。Cartwrightの式は最初の区間を計算しているのに対し、Wikipediaの記事の式は最後の積分を調整しています。適切な代数的置換が行われれば、式は示されている値になります。

[

[

[

[

[ 5 ]

[

[ 7 ]を得る。

[ 8 ]

[

[ 10 ]