音速

音速で稀に発生する局所的な凝縮現象を見せるF /A-18ホーネット

音響測定
特性	シンボル
音圧	p、SPL、L PA
粒子速度	v、SVL
粒子変位	δ
音の強さ	私、義理の妹
音響パワー	P、SWL、L WA
音エネルギー	W
音エネルギー密度	わ
音への暴露	E、SEL
音響インピーダンス	Z
オーディオ周波数	AF
伝送損失	TL
v t e

音速とは、音波が弾性媒体中を伝播する際に単位時間あたりに移動する距離です。より簡単に言えば、音速とは振動が伝わる速さです。20℃（68℉）の空気中の音速は約343m  /s（1,125 フィート/秒、1,235km  /h、767mph  、 667kn  ）です。1km 以内​2.92秒または1マイル4.69秒。これは温度と音波が伝播する媒体に大きく依存します。

0℃（32℉）の乾燥空気（海面14.7psi）での音速は約331m/s（1,086ft/s、1,192km/h、740mph、643kn）である。^{[ 1 ]}

理想気体中の音速は、その温度と組成のみに依存します。乾燥空気中の音速は周波数と圧力にほとんど依存せず、理想的な挙動からわずかに逸脱します。

口語では、音速とは空気中の音波の速度を指します。しかし、音速は物質によって異なります。一般的に、音は気体中で最も遅く、液体中で最も速く、固体中で最も速く伝わります。

例えば、音は空気中では343m/s 、淡水では20℃（68℉）の温度では1481m/s ^{[ 2 ]}（4.3倍強）で、鉄では5120 m/s（約15倍）です。ダイヤモンドのような非常に硬い物質では、音速は12,000 m/s（39,000 ft/s）^{[ 3 ]}で伝わります 。これは空気中の約35倍で、通常の条件下で伝わる音速のほぼ最高速度です。

理論上、音速は実際には振動の速度です。固体中の音波は、気体や液体と同様に圧縮波と、固体でのみ発生する横波と呼ばれる異なる種類の音波で構成されています。地震学で見られるように、固体中の横波は通常、圧縮波とは異なる速度で伝わります。固体中の圧縮波の速度は、媒体の圧縮率、横弾性係数、および密度によって決まります。横波の速度は、固体材料の横弾性係数と密度によってのみ決まります。

流体力学では、流体媒体（気体または液体）中の音速は、媒体中を移動する物体の速度の相対的な尺度として用いられます。物体の速度と（同じ媒体中の）音速の比は、物体のマッハ数と呼ばれます。音速（マッハ1 ）よりも速い速度で移動する物体は、超音速で移動していると言われます。

地球

地球の大気圏では、音速は高度が高いときの約 295 m/s (1,060 km/h、660 mph) から、高温時の約 355 m/s (1,280 km/h、790 mph) まで大きく変化します。

歴史

ピタゴラス学派のアルキタスは、高音はより速く伝わると教え、この考えはその後のアカデミーやペリパトスなどの哲学者、おそらくアリストテレスにも受け入れられた。^{[ 4 ]}

アイザック・ニュートン卿が1687年に著した『プリンキピア』には、空気中の音速を979フィート/秒（298 m/s）と計算した値が含まれています。これは約15%低い値です。^{[ 5 ]}この食い違いは、主に（当時は未知であった）音波中の急激な温度変動の影響を無視したことに起因しています（現代の用語で言えば、音波による空気の圧縮と膨張は断熱過程であり、等温過程ではありません）。ニュートンはその後、「空気中の固体粒子の粗さ」など、様々な調整係数を考案し、最終的に実験値と一致する数値を得ました。 ^{[ 6 ]}ラグランジュとオイラーは両者ともこの食い違いを説明しようとしましたが、失敗しました。この食い違いは最終的にピエール＝シモン・ラプラスによって正しく説明されました。^{[ 7 ]}天文力学論において、彼は1819年のクレマン＝デゾルムの実験結果を用いて、空気の熱容量比が1.35と測定された。これにより、音速に関して理論と実験がほぼ一致することが示された。数年後には現代の値である1.40が発見され、完全な一致が得られた。^{[ 8 ]}

17世紀には、音速を正確に測定する試みがいくつか行われました。1630年、マラン・メルセンヌは2つの値を発見しました。銃の閃光が見えてから一定距離でその音が聞こえるまでの時間（秒振り子）を測定した際、彼は1,380パリ・フィート/秒（448 m/秒）という値を発見しました。一方、銃を発射してから一定距離の反射面から反響音が聞こえるまでの時間を測定した際、彼は970パリ・フィート/秒という値を発見しました。このことから、反響音は反響しない音よりも遅いという理論が生まれました。その後の実験者のほとんどは、彼の最初の方法のみを使用しました。^{[ 9 ]}

1635年にピエール・ガッサンディは1,473パリフィート/秒^{[ 10 ]}、ロバート・ボイルは1,125パリフィート/秒^{[ 11 ]}を発見した。 1650年にはアカデミア・デル・チメントのG.A.ボレッリとV.ヴィヴィアーニが350メートル/秒を発見した。^{[ 12 ]} 1709年にはアップミンスターの牧師ウィリアム・ダーハムが、音速のより正確な測定値である1,072パリフィート/秒を発表した。^{[ 13 ] [ 11 ]}（パリフィートは325 mm。これは、1959年に公式に定義された、現在一般的に使用されている標準的な「国際フィート」よりも長い。304.8 mmで、20 °C（68 °F）での音速は1,055パリアンフィート/秒になります。1636年から1791年の間に測定された音速の表については、 ^{[ 7 ]を参照してください。}

ダーハムはアップミンスターのセントローレンス教会の塔から望遠鏡を使って遠くの散弾銃の閃光を観測し、半秒振り子で銃声が聞こえるまでの時間を測定した。ノースオッケンドン教会を含む地元のランドマークから銃声が測定された。距離は三角測量によって分かっていたので、音の伝わる速度が計算できた。^{[ 14 ]}彼はこれを様々な状況下で何度も測定し、風速、気圧、気温、湿度への音速の依存性を調べた。例えば、風が観測者に向かって吹いているときは音速が速く、逆もまた同様であることを発見した。彼は夏も冬も音速が同じだったので気温は音速に影響しないと考えていた。^{[ 15 ]}また、雨や霧が音速を低下させるという彼の結論も誤りであり、この結論はティンダルが反証するまで受け入れられていた。^{[ 16 ] : 6}

初期の測定では音速が一致しないことが判明し、風速と気温が音速を変える可能性があると疑われました。1740年、G・L・ビアンコーニは空気中の音速が気温とともに増加することを示しました。^{[ 17 ] [ 8 ]}パリ科学アカデミーは1738年に大砲を音源として用い、無風時の0℃における音速は332m/sであることを発見しました。これは現代の許容値の1%以内でした。^{[ 8 ]}

クラドニは、空気の管と固体の棒の中の音の高さを比較することで固体中の音速を測定し、錫の中の音速は空気中の約 7.5 倍、銅の中の音速は約 12 倍であることを発見しました。^{[ 16 ] : 7} ビオは1808 年に長さ約 1000 メートルの鉄管内の音速を測定し、それが空気中の 10.5 倍であることを発見しましたが、これはあくまでも推定値の 1 桁に過ぎないと考えていました。というのも、彼の時間測定の精度は 0.5 秒で、音がパイプを通って伝播するのに実際に必要な時間よりも長かったからです。^{[ 18 ] [ 19 ]}

水中の音速の最初の測定は、 1826年にジャン＝ダニエル・コラドンとチャールズ・スタームによってレマン湖で行われた。彼らは10km離れた2隻の船に乗っていた。コラドンはレバーを繰り返し押すことで、水面上の少量の火薬に点火し、同時に水中のベルを鳴らした。スタームは水中チューブでベルの音を聞き、音が聞こえるまでの時間を計測した。彼らは8℃の水中で1437.8m/sという値を測定した。これは現代の値と1m/sの差がある。^{[ 16 ] : 34–36 [ 8 ]}彼らはこの結果をモノグラフで発表した。^{[ 20 ]}

サミュエル・アーンショーは1860年に、1822年に行われた実験において、大砲の音が、その横に立って「発射！」と叫ぶ士官よりも先に聞こえたと報告した。彼は、この実験結果から、十分な音量の音は空気中に不連続性（現代の言葉で言えば衝撃波）を生み出し、それが通常の音波よりも速く伝播するのではないかと仮説を立てた。^{[ 21 ]}

圧縮波と横波

圧力パルス波、または圧縮波（縦波）は平面内に閉じ込められます。これは流体（気体および液体）中を伝わる唯一の音波です。圧力波は、他の種類の波（横波、下記参照）とともに固体中を伝わることもあります。

横波は、当初は平面内に閉じ込められていた原子に作用します。この新たな種類の音波（弾性波の一種）は、固体中の弾性によって支えられる横方向のせん断運動を必要とするため、固体中のみを伝搬します。横方向のせん断運動は、波の伝搬方向に垂直な任意の方向に発生する可能性があります（ここでは、平面に直角なせん断方向のみを示しています）。さらに、直角のせん断方向は時間と距離によって変化する可能性があり、その結果、せん断波の異なる種類の偏光が生じます。

気体や液体では、音は圧縮波で構成されます。固体では、波は2つの異なるタイプとして伝播します。縦波は進行方向の圧縮と減圧に関連し、気体と液体で同じプロセスであり、固体にも同様の圧縮タイプの波が存在します。圧縮波のみが流体（気体と液体）中を伝播します。横波（せん断波とも呼ばれる）という別のタイプの波は、弾性変形をサポートできるのは固体だけであるため、固体でのみ発生します。これは、波の進行方向に対して垂直な媒体の弾性変形によるもので、せん断変形の方向は、このタイプの波の「偏光」と呼ばれます。一般的に、横波は一対の直交偏光として発生します。

これらの異なる波（圧縮波と異なる偏波の横波）は、同じ周波数でも速度が異なる場合があります。そのため、観測者に到達する時間は異なります。極端な例として地震が挙げられますが、地震では鋭い圧縮波が最初に到達し、数秒後に横揺れの横波が到達します。

流体中の圧縮波の速度は、媒体の圧縮率と密度によって決まります。固体中の圧縮波は、流体中の圧縮波と同様に圧縮率と密度に依存しますが、さらに剪断弾性率という要素が加わります。剪断弾性率は、圧縮時の有効張力と緩和に影響を与える軸外弾性エネルギーによって圧縮波に影響を与えます。固体中でのみ発生する剪断波の速度は、固体材料の剪断弾性率と密度によってのみ決まります。

方程式

数学的表記における音速は、通常、ラテン語の「速さ」を意味するceleritasに由来するcで表されます。

一般的な流体の場合、音速cはニュートン・ラプラス方程式で与えられます。 ここで $${\displaystyle c={\sqrt {\frac {K_{s}}{\rho }}},}$$

• ${\displaystyle K_{s}}$ 剛性係数、等エントロピー体積弾性係数（または気体の場合は体積弾性係数）です。
• ${\displaystyle \rho }$ 密度です。

${\displaystyle K_{s}=\rho \left({\frac {\partial P}{\partial \rho }}\right)_{s}}$ ここで は圧力であり、微分は等エントロピー、つまりエントロピーsが一定である条件で取られます。これは、音波の伝播速度が非常に速いため、その伝播を断熱過程として近似できるためです。つまり、音波の圧力サイクル中に、顕著な熱伝導と放射が発生するのに十分な時間がないということです。 ${\displaystyle P}$

したがって、音速は物質の剛性（弾性体が加えられた力に対して変形しにくい性質）とともに増加し、密度の増加とともに減少します。理想気体の場合、体積弾性率Kは単に気体圧力に無次元断熱指数を乗じた値で、通常の圧力および温度条件下では空気の場合約1.4です。

一般的な状態方程式については、古典力学を用いると、音速cは次のように導出できる^{[ 22 ]}。

軸に平行で断面積が のパイプを速度 で伝播する音波を考えてみましょう。時間間隔 において、音波は長さ だけ移動します。定常状態では、質量流量は管の両端で同じでなければならないため、質量流束は一定で となります。ニュートンの第二法則によれば、圧力勾配力は加速度 を与えます。 ${\displaystyle v}$ ${\displaystyle x}$ ${\displaystyle A}$ ${\displaystyle dt}$ ${\displaystyle dx=v\,dt}$ ${\displaystyle {\dot {m}}=\rho vA}$ ${\displaystyle j=\rho v}$ ${\displaystyle v\,d\rho =-\rho \,dv}$ $${\displaystyle {\begin{aligned}{\frac {dv}{dt}}&=-{\frac {1}{\rho }}{\frac {dP}{dx}}\\[1ex]\rightarrow dP&=(-\rho \,dv){\frac {dx}{dt}}=(v\,d\rho )v\\[1ex]\rightarrow v^{2}&\equiv c^{2}={\frac {dP}{d\rho }}\\[1ex]\rightarrow c&={\sqrt {\left({\frac {\partial P}{\partial \rho }}\right)_{s}}}={\sqrt {\frac {K_{s}}{\rho }}}\\\end{aligned}}}$$

相対論的効果が重要である場合、音速は相対論的オイラー方程式から計算されます。

非分散媒質では、音速は音の周波数に依存しないため、エネルギー輸送速度と音の伝播速度はすべての周波数で同じです。酸素と窒素の混合物である空気は非分散媒質を構成します。しかし、空気には少量のCO ₂が含まれており、これは分散媒質であるため、超音波周波数（28kHz ）^。[ 23 ^]

分散媒質においては、音速は分散関係によって音の周波数の関数となります。各周波数成分は位相速度と呼ばれる独自の速度で伝播しますが、擾乱のエネルギーは群速度で伝播します。光波でも同じ現象が起こります。説明については 光分散を参照してください。

媒体の特性への依存

音速は変化し、音波が伝わる物質の性質に依存します。固体中における横波（またはせん断波）の速度は、せん断応力によるせん断変形（せん断弾性率と呼ばれる）と媒体の密度に依存します。固体中の縦波（または圧縮波）は、同じ2つの要因に加えて、圧縮率にも依存します。

流体においては、流体はせん断応力を伝達しないため、媒体の圧縮率と密度のみが重要な要素となります。気泡を含んだ液体のような不均質流体では、ホットチョコレート効果で示されるように、液体の密度と気体の圧縮率が音速に相加的に影響を及ぼします。

気体の場合、断熱圧縮率は熱容量比（断熱指数）を通じて圧力に直接関連しますが、圧力と密度は温度と分子量に反比例するため、温度と分子構造の完全に独立した特性のみが重要になります（熱容量比は温度と分子構造によって決定できますが、単純な分子量だけでは決定できません）。

音は、ヘリウムなどの低分子量の気体では、キセノンなどの重い気体よりも速く伝播します。単原子気体の場合、音速はその気体中の原子の平均速度の約75%です。

与えられた理想気体では分子組成は固定されているため、音速は温度のみに依存します。温度が一定であれば、密度が増加するため気体圧力は音速に影響を与えません。また、圧力と密度（これも圧力に比例）は音速に等しいが反対の影響を与え、2 つの寄与は完全に打ち消し合います。同様に、固体の圧縮波は液体の場合と同様に圧縮率と密度の両方に依存しますが、気体の場合は密度が圧縮率に寄与するため、各属性の一部は考慮されず、温度、分子量、および熱容量比のみに依存します。これらは温度と分子組成から独立して導出できます（以下の導出を参照）。したがって、与えられた単一の気体（分子量が変化しないと仮定）および狭い温度範囲（熱容量がほぼ一定）では、音速は気体の温度のみに依存するようになります。

ファンデルワールス気体方程式が使用される非理想気体の挙動レジメンでは、比例関係は正確ではなく、音速はガス圧力にわずかに依存します。

湿度は音速にわずかながら測定可能な影響を及ぼします（約0.1%～0.6%の増加を引き起こします）。これは、空気中の酸素分子と窒素分子がより軽い水分子に置き換わるためです。これは単純な混合効果です。

高度の変化と大気音響への影響

密度と圧力は高度とともに滑らかに減少しますが、温度（赤）は減少しません。音速（青）は高度における複雑な温度変化のみに依存し、密度と圧力の単独の影響は音速に打ち消し合うため、音速は高度から計算できます。成層圏と熱圏の2つの領域では、これらの領域における加熱効果により、音速は高度とともに増加します。

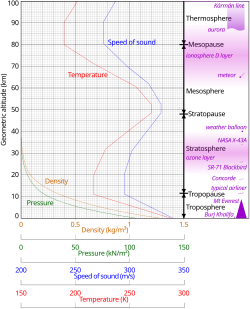
地球の大気圏において、音速に影響を与える主な要因は温度です。熱容量と組成が一定の理想気体の場合、音速は温度のみに依存します（詳細は後述の§を参照）。このような理想的なケースでは、密度の低下と高度による気圧の低下の影響は、温度の残余効果を除いて相殺されます。

気温（そして音速）は高度が上がるにつれて低下するため、11 kmでは、音は地上の聴取者から離れて上方に屈折し、音源から少し離れたところに音響の影を作ります。 ^{[ 24 ]}高さとともに音速が減少することを負の音速勾配と呼びます。

上記の傾向にはばらつきがある11 km。特に、約20 km では、オゾン層内の加熱による温度上昇により、音速は高度とともに増加します。これにより、この領域では正の音速勾配が生じます。さらに、非常に高い高度、つまり熱圏では、正の勾配の領域が存在します。90キロ。

詳細

理想気体と空気中の音速

理想気体の場合、K（上記式の体積弾性係数、固体の剛性係数 Cに相当）は次のように与えられます 。したがって、上記のニュートン・ラプラス方程式から、理想気体中の音速は次のように与えられます。 ここで $${\displaystyle K=\gamma \cdot p.}$$ $${\displaystyle c={\sqrt {\gamma \cdot {p \over \rho }}},}$$

• γは断熱指数であり、等エントロピー膨張係数とも呼ばれます。これは、定圧気体の比熱と定積気体の比熱（）の比であり、古典音波が断熱圧縮を引き起こすことで生じます。断熱圧縮では、圧縮熱が圧力脈動から逃げる時間が十分にないため、圧縮によって引き起こされる圧力に寄与します。${\displaystyle C_{p}/C_{v}}$
• pは圧力です。
• ρは密度です。

理想気体の法則を用いてpをnRT / Vに置き換え、ρをnM / Vに置き換えると、理想気体の方程式は 次のよう になる。$${\displaystyle {\begin{aligned}c_{\mathrm {ideal} }&={\sqrt {\frac {\gamma p}{\rho }}}={\sqrt {\frac {\gamma RT}{M}}}={\sqrt {\frac {\gamma kT}{m}}}\\&={\sqrt {\frac {1.380649\cdot 10^{-23}\cdot \gamma T}{m}}}\approx {\sqrt {\frac {8.314\gamma T}{M}}}\\&{\begin{cases}&={\sqrt {\frac {1.9329086\cdot 10^{-23}\cdot T}{m}}}\approx {\sqrt {\frac {11.640T}{M}}},&&\gamma ={\frac {7}{5}}\\&\approx {\sqrt {\frac {2.301\cdot 10^{-23}\cdot T}{m}}}\approx {\sqrt {\frac {13.857T}{M}}},&&\gamma ={\frac {5}{3}}\\&\approx {\sqrt {\frac {1.840\cdot 10^{-23}\cdot T}{m}}}\approx {\sqrt {\frac {11.086T}{M}}},&&\gamma ={\frac {4}{3}}\\\end{cases}}\\c_{\mathrm {dry\ air} }&\approx 20.04687087513010149970678963{\sqrt {T}}\end{aligned}}}$$

• c _idealは理想気体中の音速です。
• pは圧力です。
• ρは密度です。
• γ（ガンマ）は断熱指数である。室温では、熱エネルギーは完全に回転に分配される（回転が完全に励起される）が、量子効果によって振動モードの励起は妨げられる。運動論によれば、二原子気体（酸素や窒素など）の場合、ガンマの値は7/5 = 1.400となる。ガンマは実際には実験的に1.3991から1.403の範囲で測定されている。0 °C、空気の場合。ガンマは、アルゴンなどの単原子ガスでは5/3 = 1.667 、 Hなどの三原子分子ガスでは4/3 = 1.333です。₂Oは共線的ではない（共線的三原子ガス、例えばCO₂これは、ここでは二原子ガスに相当します。
  • γ自体は温度に依存し、低温では値が大きくなり、高温では値が小さくなります。例えば乾燥空気の場合、258.15°Kでは約1.404、293.15°Kでは約1.400、473.15°Kでは約1.398となります。
• Rはモル気体定数であり、8.314 462 618 153 24  J⋅mol ⁻¹ ⋅K ^{−1 ‍ [25 ]} ;
• kはボルツマン定数、1.380 649 × 10 ⁻²³  J⋅K ^{−1 ‍ [26 ]} ;
• Tは絶対温度です。
• Mは気体のモル質量である。乾燥空気の平均モル質量は約28.9647 g/mol（0.0289647 kg/mol）である^{[ 27 ]。}
• nはモル数です。
• mは単一分子の質量です。

この式は、音波が周囲の状態に対して小さな摂動を与え、かつ以下に示す他の条件が満たされている場合にのみ適用されます。計算されたc _airの値は、実験的に決定された値とわずかに異なることが分かっています。^{[ 28 ]}

ニュートンは熱力学の発展のほとんど以前に音速を考察していたことで有名であり、断熱計算ではなく等温計算を誤って用いた。彼の結果はγの係数を欠いていたが、それ以外は正しかった。

上記の値を数値的に代入すると、気体の音速の理想気体近似値が得られ、これは比較的低い気体圧力および密度（空気の場合、標準的な地球の海面条件を含む）において正確です。また、二原子気体の場合、γ = 1.4000を使用するには、気体が回転熱容量が完全に励起される（すなわち、分子の回転が熱エネルギーの「区画」または貯蔵庫として十分に利用される）のに十分な温度範囲に存在する必要があります。しかし同時に、分子の振動モードが熱容量に寄与しない（すなわち、最小エネルギーモードより上のすべての振動量子モードは、この温度では十分な数の分子が存在できないほど高いエネルギーを持つため、振動にはほとんど熱が流入しない）ほど低い温度である必要があります。空気の場合、これらの条件は室温で満たされ、室温よりかなり低い温度でも満たされます（以下の表を参照）。この現象に関するより詳細な議論については、 比熱容量における気体のセクションを参照してください。

空気については、略語を導入します $${\displaystyle R_{*}=R/M_{\mathrm {air} }.}$$

熱容量比（緑）と切断テイラー展開（赤）に基づく乾燥空気中の音速の近似値

さらに摂氏温度θ = T −273.15 Kは、0 °C (273.15 K) 付近の空気速度を計算するのに役立ちます。次に、乾燥空気の場合、 $${\displaystyle {\begin{aligned}c_{\text{air}}&={\sqrt {\gamma \cdot R_{*}\cdot T}}={\sqrt {\gamma \cdot R_{*}\cdot (\theta +273.15)}}\\&={\sqrt {\gamma \cdot R_{*}\cdot 273.15\,\mathrm {^{\circ }K} }}\cdot {\sqrt {1+{\frac {\theta }{273.15}}}}\\R&=8.314\,462\,618\,153\,24~{\frac {\text{J}}{\mathrm {mol\cdot {^{\circ }K}} }}\\M_{\text{air}}&=0.028\,964\,7~{\frac {\text{kg}}{\text{mol}}}\\R_{*}&\approx 287.055\,022\,773\,853\,725\,396\,776\,076\\\gamma &=1.4000~{\text{(Ideal diatomic gas)}}\\c_{\text{air}}&\approx 331.32{\frac {\text{m}}{\text{s}}}\times {\sqrt {1+{\frac {\theta }{273.15}}}}\\\end{aligned}}}$$

最後に、残りの平方根の 二項近似（θが0に非常に近いと仮定）は、$${\displaystyle {\begin{aligned}c_{\mathrm {air} }&\approx 331.32{\frac {\text{m}}{\text{s}}}\times \left(1+{\frac {\theta }{546.3}}\right)\\&\approx 331.32{\frac {\text{m}}{\text{s}}}+0.606\theta {\frac {\mathrm {m} }{\text{s}}}\end{aligned}}}$$

摂氏0度では、二項近似は不正確さをもたらしませんが、γは不正確さをもたらします。その温度で完全に乾燥した空気の熱容量比は実際には約1.403です。訂正：

$${\displaystyle {\begin{aligned}\gamma &=1.403~({\text{dry air at }}\theta =0)\\c_{\mathrm {air} }&\approx 331.67{\frac {\text{m}}{\text{s}}}\times \left(1+{\frac {\theta }{546.3}}\right)\\&\approx 331.67{\frac {\text{m}}{\text{s}}}+0.607\theta {\frac {\mathrm {m} }{\text{s}}}\end{aligned}}}$$

2つの式の結果を比較したグラフが右側にあります。音速として、わずかに正確な値である331.5 m/s (1,088 ft/s)を使用しています。0 ℃ ^{[ 29 ] : 120 -121}

風のせん断による影響

音速は温度によって変化する。通常、高度が上昇するにつれて温度と音速は低下するため、音は地上の聴取者から上方に屈折し、音源からある程度離れた場所に音響の影を形成する。 ^{[ 24 ]} 4m/(s · km)の風速は、典型的な温度減率に等しい屈折を引き起こす可能性がある。7.5 °C/km。^{[ 30 ]}風勾配の値が大きいほど、音は風下方向の地表に向かって下方に屈折し、^{[ 31 ]}風下側の音響影が消えます。これにより、風下の音の可聴性が高まります。この風下屈折効果は風勾配があるために発生するものであり、音が風によって運ばれるという事実は重要ではありません。^{[ 32 ]}

音の伝播に関しては、風速の高さに対する指数関数的変化は次のように定義される 。 ^{[ 33 ]}$${\displaystyle {\begin{aligned}U(h)&=U(0)h^{\zeta },\\{\frac {\mathrm {d} U}{\mathrm {d} h}}(h)&=\zeta {\frac {U(h)}{h}},\end{aligned}}}$$

• U ( h ) は高さhにおける風速である。
• ζは地表面粗さに基づく指数係数であり、通常は0.08～0.52の範囲です。
• dU / dh ( h ) は高さ h に対する風速の変化率であり、固定高さhにおける予想される風勾配に比例します。

1862年のアメリカ南北戦争のイウカの戦いでは、北東の風によって増強されたと考えられる音響の影により、北軍の2個師団が戦闘に参加できなかった。^{[ 34 ]}彼らは戦闘の音しか聞こえなかったため、風下10キロ（6マイル）。^{[ 35 ]}

テーブル

標準大気中：

• T ₀は273.15 K (=0℃ =32 °F）、理論値は331.3 m/s (=1 086 .9 フィート/秒=時速1193キロ=741.1 mph = 644.0 kn）。値は331.3からただし、参考文献には331.6 m/sと記載されています。
• T ₂₀は293.15 K (=20℃ =68°F）、値は343.2 m/s (=1 126 .0 フィート/秒=時速1236キロ=767.8 mph = 667.2 kn );
• T ₂₅は298.15 K (=25℃ =77°F）、値は346.1 m/s (=1 135 .6 フィート/秒=時速1246キロ=774.3 mph = 672.8 kn )。

実際、理想気体を仮定すると、音速cは温度と組成のみに依存し、圧力や密度には依存しません（これらは一定の温度で同期して変化し、相殺されるため）。空気はほぼ理想気体です。空気の温度は高度によって変化するため、標準大気を用いた場合の音速は次のように変化します。ただし、実際の状況は異なる場合があります。

空気の性質に対する温度の影響

摂氏温度θ [ °C ]	音速c [ m / s ] ​	空気の密度ρ [ kg / m ^3 ]	特性音響インピーダンスz 0 [ Pa ⋅ s / m ]
35	351.88	1.1455	403.2
30	349.02	1.1644	406.5
25	346.13	1.1839	409.4
20	343.21	1.2041	413.3
15	340.27	1.2250	416.9
10	337.31	1.2466	420.5
5	334.32	1.2690	424.3
0	331.30	1.2922	428.0
−5	328.25	1.3163	432.1
−10	325.18	1.3413	436.1
−15	322.07	1.3673	440.3
−20	318.94	1.3943	444.6
−25	315.77	1.4224	449.1

通常の大気条件では、温度、つまり音速は高度によって変化します。

高度	温度	MS	km/h	時速	知っている
海面	15℃（59°F）	340	1,225	761	661
11,000 m～20,000 m（民間ジェット機の巡航高度、および初の超音速飛行）	−57℃（−70 °F )	295	1,062	660	573
29,000メートル（X-43Aの飛行）	−48℃（−53 °F )	301	1,083	673	585

周波数とガス組成の影響

一般的な物理的考慮事項

音波が伝わる媒体は必ずしも断熱的に反応するわけではなく、その結果、音速は周波数によって変化する可能性がある。^{[ 36 ]}

極端な減衰による音速の概念の限界も懸念される。海面における高周波数の減衰は、大気圧の低下、あるいは平均自由行程の増加に伴って、より低い周波数にも適用される。このため、音速の概念（ゼロに近づく周波数を除く）は、高高度では徐々に適用範囲が狭まる。^{[ 28 ]}音速の標準的な式は、音波の波長が気体中の分子の平均自由行程よりもかなり長い場合にのみ、妥当な精度で適用される。

気体の分子組成は、分子の質量（M）と熱容量の両方に寄与し、音速に影響を与えます。一般的に、同じ分子量の場合、単原子気体の音速はわずかに（9%以上）速くなります。これは、単原子気体のγ（5/3 = 1.66 ...）が二原子気体（7/5 = 1.4）よりも高いためです。したがって、同じ分子量の場合、単原子気体の音速は次の式で表されます。 $${\displaystyle {c_{\mathrm {gas,monatomic} } \over c_{\mathrm {gas,diatomic} }}={\sqrt {{5/3} \over {7/5}}}={\sqrt {25 \over 21}}=1.091\ldots }$$

この9%の差は、分子量が4のヘリウムと重水素の室温での音速の典型的な比率となります。ヘリウム中の音速は重水素よりも速く伝わります。これは、ヘリウム分子が圧縮による熱エネルギーを並進運動によってのみ蓄えることができ、回転運動によって蓄えることができないため、断熱圧縮によってヘリウムがより多く加熱されるためです。したがって、ヘリウム分子（単原子分子）は音波としてより速く伝わり、より速く音を伝達します。（音速は気体中の平均分子速度の約70%で伝わります。この数値は単原子気体では75%、二原子気体では68%です。）

この例では、温度が十分に低く、熱容量が分子振動の影響を受けないと仮定しています（熱容量を参照）。振動モードはガンマを1に近づけるだけで済みますが、多原子気体の振動モードは温度に影響を与えない熱を蓄える追加の手段となるため、分子速度と音速には影響を与えません。したがって、温度上昇と振動熱容量の影響により、単原子分子と多原子分子の音速の差は拡大しますが、音速は単原子分子の方が大きいままです。

空気への実用化

空気中の音速に影響を及ぼす最も重要な要因は、間違いなく温度です。音速は絶対温度の平方根に比例し、約1℃あたり0.6m/sです。そのため、管楽器の音程は温度が上昇するにつれて高くなります。

音速は湿度によって速くなります。湿度0%と100%の差は約標準圧力および温度では1.5 m/sですが、湿度の影響の大きさは温度とともに劇的に増加します。

周波数と圧力への依存性は、実用上は通常は重要ではありません。乾燥した空気中では、音速は約周波数が0.1 m/sから上昇するにつれて10Hzから100 Hz。それ以上の可聴周波数の場合100 Hzでは比較的一定です。音速の標準値は、波長が平均自由行程に比べて大きい低周波数の限界で引用さ​​れています。^{[ 37 ]}

上に示したように、近似値1000/3 = 333.33...m/sは、5℃は、あらゆる「通常の」外気温（少なくとも温帯気候においては）の近似値です。そのため、雷がどのくらい遠くまで落ちたかを判断するための一般的な目安として、稲妻が閃光を開始してから雷鳴が轟き始めるまでの秒数を数え、それを3で割ります。その結果が、最も近い落雷地点までの距離（キロメートル）です。または、秒数を5で割ると、マイルでのおおよその距離になります。

マッハ数

マッハ数は航空力学において有用な量であり、空気速度と局所音速の比です。高度においては、前述の理由により、マッハ数は温度の関数となります。しかし、航空機の飛行計器は、温度ではなく圧力差を用いてマッハ数を計算します。特定の圧力は特定の高度、つまり標準温度を表すという前提に基づいています。ピトー管が感知するよどみ圧は、速度だけでなく高度にも依存するため、航空機の飛行計器はこのように動作する必要があります。

実験方法

空気中の音速を測定するにはさまざまな方法があります。

空気中の音速を比較的正確に推定した最初の方法は、ウィリアム・ダーハムによるもので、アイザック・ニュートンもこれを認めています。ダーハムは、イギリスのアップミンスターにあるセント・ローレンス教会の塔の上に望遠鏡を設置していました。穏やかな日に、同期した懐中時計を助手に渡し、助手は事前に決めた時間に、数マイル離れた田園地帯の目立つ地点から散弾銃を発射します。これは望遠鏡で確認できます。次に、ダーハムは、半秒振り子を使用して、銃煙が見えてから音が到達するまでの間隔を測定しました。銃が発射された場所からの距離は三角測量によって求められ、単純な割り算 (距離/時間) で速度が求められました。最後に、さまざまな距離で多数の観測を行うことで、半秒振り子の不正確さを平均化し、音速の最終的な推定値を得ることができました。現代のストップウォッチのおかげで、この方法は200～400メートルほどの短い距離でも使用でき、ショットガンのような大きな音を出すものも必要ない。

シングルショットタイミング法

最もシンプルな概念は、2つのマイクとデジタルストレージスコープなどの高速録音機器を用いて測定する方法です。この方法は、以下の考え方に基づいています。

音源と 2 つのマイクが一直線上に配置され、音源が一方の端にある場合、次のことが測定できます。

1. マイク間の距離 ( x ) をマイク基底と呼びます。
2. 異なるマイクに到達する信号間の到着時間（遅延）（t）。

するとv = x / tとなります。

その他の方法

これらの方法では、時間の測定が時間の逆数 (周波数) の測定に置き換えられました。

クント管は、小さな体積内での音速を測定するのに使用できる実験の一例です。あらゆる気体中の音速を測定できるという利点があります。この方法では、粉末を用いて音の節と腹を人間の目で確認できるようにします。これはコンパクトな実験装置の一例です。

長いパイプを樽の水に浸し、その口元に音叉を近づけます。このシステムでは、パイプ内の空気柱の長さが(1 + 2 n ) λ /4 （ nは整数）に等しい場合、パイプは共鳴状態になります。パイプの開口端における腹点はパイプ口のわずかに外側にあるため、共鳴点を2つ以上見つけ、それらの間の波長の半分を測定するのが最適です。

ここではv = fλとなります。

空気中の高精度測定

高精度測定を行う際には、不純物の影響が顕著になることがあります。化学乾燥剤は空気を乾燥させるのに使用できますが、サンプルを汚染してしまいます。空気は極低温で乾燥させることもできますが、これは二酸化炭素も除去してしまうため、多くの高精度測定は自然空気ではなく二酸化炭素を含まない空気を用いて行われます。2002年のレビュー^{[ 38 ]}によると、1963年にスミスとハーロウが円筒形共振器を用いて行った測定が「これまでで最も確からしい標準音速の値」を示したことが分かりました。この実験は二酸化炭素を除去した空気を用いて行われましたが、結果は実際の空気に適用できるようにこの影響を考慮して補正されました。実験は30℃だが、報告するために温度補正されている。0℃。結果は、標準温度の乾燥空気の場合、周波数が0℃から10℃の場合、331.45±0.01m/sであった。93 Hz～1,500 Hz。

非気体媒体

固体中の音速

三次元立体

固体においては、体積変形と剪断変形の両方において非ゼロの剛性が存在する。したがって、変形モードに応じて異なる速度の音波を生成することが可能である。体積変形（圧縮）と剪断変形（せん断）を生じる音波は、それぞれ圧力波（縦波）と剪断波（横波）と呼ばれる。地震においては、対応する地震波はそれぞれP波（一次波）とS波（二次波）と呼ばれる。均質な3次元固体中を伝播するこれら2種類の波の音速は、それぞれ^{[ 29 ]} で与えられる。 ここで $${\displaystyle c_{\mathrm {solid,p} }={\sqrt {\frac {K+{\frac {4}{3}}G}{\rho }}}={\sqrt {\frac {E(1-\nu )}{\rho (1+\nu )(1-2\nu )}}},}$$ $${\displaystyle c_{\mathrm {solid,s} }={\sqrt {\frac {G}{\rho }}},}$$

• Kは弾性材料の体積弾性率です。
• Gは弾性材料のせん断弾性率です。
• Eはヤング率です。
• ρは密度である。
• νはポアソン比です。

最後の量はE = 3K(1 − 2ν)であるため、独立した量ではありません。圧力波の速度は材料の圧力とせん断抵抗の両方に依存しますが、せん断波の速度はせん断抵抗のみに依存します。

一般的に、圧力波はせん断波よりも物質中を速く伝わります。地震においては、これが地震の発生に先立って、急激な上下方向の衝撃が起こり、その後に横方向の運動を引き起こす波が到達する理由です。例えば、典型的な鋼合金の場合、K = 170 GPa、G = 80 GPa、p =7700 kg/m ³となり、圧縮速度c _solid,pは6,000 m/sとなります。 ^{[ 29 ]}これは、（おそらく異なる）種類の鋼に対して実験的に測定されたc _solid,p 5,930 m/sとほぼ一致しています。 ^{[ 39 ]}同じ数値を使用して、 せん断速度c _solid,sは3,200 m/sと推定されます

半導体固体中の音速は、その中の電子ドーパントの量に非常に敏感である。^{[ 40 ]}

特定の固体における縦波および横波音速

材料	略語	密度${\displaystyle {\frac {kg}{m^{3}}}}$	${\displaystyle C_{L}{\frac {m}{s}}}$	${\displaystyle C_{s}{\frac {m}{s}}}$	参照
ルカロックス	${\displaystyle {\ce {Al2O3}}}$	3958	10614±79	6374±228	[ 41 ]
アルミニウムオキシナイトライド	アロン	3678	10091±90	6015	[ 41 ]
アルミニウム、1100	アル-1100	2693	6313±32	3115±3	[ 41 ]
アルミニウム、5052 H32	AL-5052	2674	6146±42	3122±42	[ 41 ]
真鍮	真鍮	8520	4457±18	2272±141	[ 41 ]
銅	銅	8924	4664±32	2356±6	[ 41 ]
マグネシウム	マグネシウム	1700	5827±51	3186	[ 41 ]
モリブデン	モ	10196	6381±21	3553	[ 41 ]
ポリ乳酸	人民解放軍	1191	1908±6	970±10	[ 41 ]
ポリメチルペンテン	TPX	833	2133±17	1065±13	[ 41 ]
ポリキャスト	PMMA	1180	2786±27	1409±16	[ 41 ]
サファイア（Z軸）	${\displaystyle {\ce {Al2O3}}}$	3990	11100	6040	[ 41 ]
シリカ、フューズドクォーツ	${\displaystyle {\ce {SiO2}}}$	2203	5512±25	3743	[ 41 ]
スチール、ステンレス、304	SS-304	7834	5912±97	3420±4	[ 41 ]
スチール、ステンレス、316	SS-316	7821	5882±20	3167±28	[ 41 ]
スチール、QTLCS	QTLCS	7817	5677±12	3192±35	[ 41 ]
鋼、CRS A36/1008 軟鋼	A36/1008	7896	5596	3154	[ 41 ]
スチール、AR500	AR500	7787±88	5697±37	3254±53	[ 41 ]
スチール、G90亜鉛メッキ	G90	7832	5759	3229	[ 41 ]
スチール、4130クロモリ	4130	7965	5604±9	3306±65	[ 41 ]
タンタル	タ	16652	4091±29	2004±56	[ 41 ]
チタン（窒化物コーティング）	ティ	4505±1	6114±15	3205±67	[ 41 ]
チタングレード5	Ti-6Al-4V	4422	6175±53	3460±100	[ 41 ]
タングステン	W	19198	5090±38	2852	[ 41 ]
亜鉛	亜鉛	7193±72	3842±34	2308±43	[ 41 ]
ジルコニア	${\displaystyle {\ce {ZrO2}}}$	6081±1	6864±52	3597±19	[ 41 ]

1次元立体

金属などの硬い物質における圧力波の音速は、その物質の「長い棒」で表す場合があり、その場合、音速の測定が容易になります。直径が波長よりも短い棒の場合、純粋な圧力波の音速は簡略化されて、次のように表されます。^{[ 29 ] : 70} ここで、Eはヤング率です。これは、ヤング率がせん断弾性率に置き換わっている点を除けば、せん断波の式に似ています。長い棒における圧力波の音速は、均質な3次元固体における同じ音速よりも常にわずかに遅くなり、2つの異なる種類の物体における音速の比は、物質の ポアソン比に依存します。$${\displaystyle c_{\mathrm {solid} }={\sqrt {\frac {E}{\rho }}},}$$

液体中の音速

水中の音速と温度

流体では、剛性がゼロにならないのは体積変形のみです (流体はせん断力に耐えません)。

したがって、流体中の音速は次のように表されます。 ここで、Kは流体の 体積弾性係数です。$${\displaystyle c_{\mathrm {fluid} }={\sqrt {\frac {K}{\rho }}},}$$

水

淡水中では、音速は約1481 m/sで20℃（オンライン計算機については、以下の外部リンクセクションを参照してください）。^{[ 42 ]}水中音の応用としては、ソナー、音響通信、音響海洋学などがあります。

海水

2005年版世界海洋地図帳に基づく、太平洋ハワイ北部における音速と水深の関係。SOFARチャンネルは、水深約750メートルで音速が最小となる地点をカバーしている。

気泡や浮遊物のない塩水中では、音速は約1500 m/s (1 500 .235 m/sで1000 キロパスカル、海水中の音速は圧力（したがって深さ）、温度（温度^変化）に依存する。1℃～4 m/s）、塩分濃度（1 ‰～音速は、一般的に音速の約1倍（約1 m/s）の変数で表され、これらの変数から音速を正確に計算するための経験式が導出されている。^{[ 44 ] [ 45 ]}音速に影響を与える他の要因は小さい。ほとんどの海域では水温が深度とともに低下するため、音速の深さに対するプロファイルは数百メートルの深さで最小値まで低下する。最小値より下では、圧力の上昇効果が温度の低下効果を上回り、音速は再び上昇する（右）。^{[ 46 ]}詳細については、Dushaw et al. ^{[ 47 ]を参照のこと。}

海水中の音速に関する実験式はマッケンジーによって示されている ： ^{[ 48 ]}$${\displaystyle c(T,S,z)=a_{1}+a_{2}T+a_{3}T^{2}+a_{4}T^{3}+a_{5}(S-35)+a_{6}z+a_{7}z^{2}+a_{8}T(S-35)+a_{9}Tz^{3},}$$

• Tは摂氏温度です。
• Sは千分率で表した塩分濃度です。
• zはメートル単位の深さです。

定数a ₁、a ₂、...、a ₉は チェック値を持つ$${\displaystyle {\begin{aligned}a_{1}&=1,448.96,&a_{2}&=4.591,&a_{3}&=-5.304\times 10^{-2},\\a_{4}&=2.374\times 10^{-4},&a_{5}&=1.340,&a_{6}&=1.630\times 10^{-2},\\a_{7}&=1.675\times 10^{-7},&a_{8}&=-1.025\times 10^{-2},&a_{9}&=-7.139\times 10^{-13},\end{aligned}}}$$ 1 550 .744 m/s（T =）25℃、 S = 35 ppm、 z = 1,000 m。この式の標準誤差は塩分濃度25～ 40pptの場合、音速は0.070 m/sです。オンライン計算機については、 技術ガイド「海水中の音速」をご覧ください。

（音速と水深のグラフは、マッケンジーの式と直接相関しません。これは、水深によって水温と塩分濃度が異なるためです。水温と塩分が一定であれば、式自体は水深とともに常に増加します。）

海水中の音速に関する他の式は、広範囲の条件で正確ですが、はるかに複雑です。例えば、VAデルグロッソ^{[ 49 ]}やチェン・ミラーロ・リーの式^{[ 47 ] [ 50 ]などがあります。}

プラズマ中の音速

電子がイオンよりも高温である（ただし、あまり高温ではない）一般的な場合のプラズマ中の音速は、次の式で与えられます（ここを 参照 ）。 $${\displaystyle c_{s}=\left({\frac {\gamma ZkT_{\mathrm {e} }}{m_{\mathrm {i} }}}\right)^{1/2}=\left({\frac {\gamma ZT_{e}}{\mu }}\right)^{1/2}\times 90.85~\mathrm {m/s} ,}$$

• m _iはイオンの質量です。
• μはイオン質量と陽子質量の比です。μ = mi _/ m _p ;
• T _eは電子温度です。
• Zは電荷状態です。
• kはボルツマン定数です。
• γは断熱指数です。

気体とは対照的に、圧力と密度はそれぞれ別の種によって与えられます。圧力は電子によって、密度はイオンによって与えられます。この2つは変動する電場を介して結合しています。

火星

火星における音速は周波数の関数として変化します。高周波数の音は低周波数の音よりも速く伝わります。レーザーからの高周波数の音は250 m/s（820 ft/s）で伝わりますが、低周波数の音は240 m/s（790 ft/s）で伝わります。^{[ 51 ]}

グラデーション

音が三次元的に全方向に均等に広がる場合、強度は距離の2乗に反比例して低下します。しかし、海中には「深海音響チャンネル」またはSOFARチャンネルと呼ばれる層があり、音波を特定の深度に閉じ込めることができます。

SOFARチャンネルでは、音速は上下の層よりも遅くなります。光波が屈折率の高い領域に向かって屈折するのと同様に、音波は速度が低下する領域に向かって屈折します。その結果、光がガラス板や光ファイバーに閉じ込められるのと同じように、音は層内に閉じ込められます。つまり、音は基本的に2次元に閉じ込められているのです。2次元では、音の強度は距離の逆数に比例して低下します。そのため、音波は検知できないほど弱くなるまで、はるかに遠くまで到達することができます。

大気圏でも同様の現象が起こります。モーグル計画では、この現象を利用して、かなり遠くに ある核爆発を検知することに成功しました。

参照

• 音響弾性効果
• 弾性波
• 2番目の音
• ソニックブーム
• 防音壁
• 元素の音速
• 水中音響
• 振動
• ベル X-1

参考文献

1. 「音速計算機」 .アメリカ国立気象局. 2021年7月23日閲覧。
2. マグロウヒル科学技術百科事典：索引を含む20巻の国際参考図書。第17巻（第10版以降）。ニューヨーク：マグロウヒル。2012年。7ページ。ISBN 978-0-07-179273-8。
3. CR Nave. 「音速」 . HyperPhysics . ジョージア州立大学物理天文学部. 2022年10月24日閲覧。
4. Pöhlmann, Egert (2020)、「音響学」、古代ギリシャ・ローマ音楽入門、John Wiley & Sons, Ltd、pp.  243– 256、doi : 10.1002/9781119275510.ch18、ISBN 978-1-119-27551-0
5. 「音速」 . mathpages.com . 2015年5月3日閲覧。
6. ウェストフォール, リチャード・S. (1973年2月23日). 「ニュートンとファッジファクター」 .サイエンス. 179 (4075): 751– 758. Bibcode : 1973Sci...179..751W . doi : 10.1126/science.179.4075.751 . PMID 17806284 . 
7. フィン、バーナード・S.（1964年3月）「ラプラスと音速」 Isis.55 ( 1) : 7–19.doi : 10.1086 / 349791.ISSN0021-1753 . 
8. Lindsay, R. Bruce (1966年4月1日). 「音響の​​物語」 .アメリカ音響学会誌. 39 (4): 629– 644. Bibcode : 1966ASAJ...39..629L . doi : 10.1121/1.1909936 . ISSN 0001-4966 . PMID 5326409 .  
9. Gouk, Penelope M. (1982). 「初期王立協会における音響学 1660-1680」 .ロンドン王立協会記録. 36 (2): 155–175 . doi : 10.1098/rsnr.1982.0009 . ISSN 0035-9149 . JSTOR 531772 .  
10. レニハン、気象庁 (1951)。 「メルセンヌとガッサンディ：サウンドの歴史の初期の章」。アクスティカ。1 (2)：96～ 99。
11. ポール・マーディン（2008年12月25日）『栄光の子午線：地球測量競争における危険な冒険』シュプリンガー・サイエンス＆ビジネス・メディア、pp.  35– 36. ISBN 9780387755342。
12. ロッシング、トーマス（2007）、「音響学の簡潔な歴史」、シュプリンガー・ハンドブック・オブ・アコースティックス、シュプリンガー、ニューヨーク、ニューヨーク、pp.  9– 24、Bibcode：2007shac.book....9R、doi：10.1007/978-0-387-30425-0_2、ISBN 978-0-387-30425-0
13. モツ、ソニ; W. ダーラム (1708)。「Soni Motu、Aliisque ad id Attinentibus、Factae a Reverendo DW Derham Ecclesiae Upminsteriensis Rectore、および Societatis Regalis Londinensis Socio の実験と観察」。哲学的な取引。26 : 2–35。ISSN 0260-7085。​​ JSTOR 103216。  
14. フォックス、トニー (2003).エセックスジャーナル. エセックス建築歴史協会. pp.  12– 16.
15. エンブルトン、トニー・FW；デイグル、ジル・A.（1977年）「12 大気伝播」90-3052 航空機の航空音響学：理論と実践。
16. ベイヤー、ロバート・T. (1999). 『現代の音：音響の200年』 ニューヨーク：AIPプレス. ISBN 978-0-387-98435-3。
17. ブランカニ、イオアンネス (1744)。 「Observationes physicae variae」[さまざまな物理的観察]。De Bononiensi Scientiarum et Artium Instituto Atque Academia Commentarii (ラテン語)。２．ボローニャ: 365 – 366。
18. フランケル、ユージン (1977). 「JBビオとナポレオン時代フランスにおける実験物理学の数学的研究」 .物理科学史研究. 8 : 33–72 . doi : 10.2307/27757367 . ISSN 0073-2672 . JSTOR 27757367 .  
19. ビオ、JB (1809)。 「Sur la propagation duson à travers les corps Solides」[固体を通した音の伝播について]。メモワール・ダルクイユ（フランス語）。2：405～ 443。
20. コラドン、ダニエル;シュトゥルム、シャルル＝フランソワ (1887)。Mémoire sur la Compression des Liquides et la vitesse du Son dans l'eau (フランス語)。ジュネーブ：シューハルト。
21. Döge, Torsten; Gebbeken, Norbert (2014), Stein, Erwin (ed.), "Historical Development of the Knowledge of Shock and Blast Waves" , The History of Theoretical, Material and Computational Mechanics - Mathematics Meets Mechanics and Engineering , Berlin, Heidelberg: Springer, pp.  249– 265, doi : 10.1007/978-3-642-39905-3_15 , ISBN 978-3-642-39905-3
22. 「17.2 音速 | 大学物理学 第1巻」 courses.lumenlearning.com . 2020年1月24日閲覧。
23. Dean, EA (1979年8月).大気の音速への影響, 国防技術情報センター技術報告書
24. エベレスト、F. (2001). 『音響マスターハンドブック』 ニューヨーク: マグロウヒル. pp.  262– 263. ISBN 978-0-07-136097-5。
25. 「2022 CODATA値：モル気体定数」。NISTの定数、単位、不確かさに関する参考資料。NIST 。2024年5月。 2024年5月18日閲覧。
26. 「2022 CODATA値：ボルツマン定数」。定数、単位、不確かさに関するNISTリファレンス。NIST。2024年5月。 2024年5月18日閲覧。
27. エンジニアリングツールボックス 空気の分子量
28. 米国標準大気、1976年、米国政府印刷局、ワシントンD.C.、1976年。
29. キンスラー, LE; フレイ, AR; コッペンス, AB; サンダース, JV (2000). 『音響の基礎』（第4版）. ニューヨーク: ジョン・ワイリー・アンド・サンズ. ISBN 0-471-84789-5。
30. ウマン、マーティン（1984年）『ライトニング』ニューヨーク：ドーバー出版、ISBN 978-0-486-64575-9。
31. Volland, Hans (1995).大気電気力学ハンドブック. ボカラトン: CRC Press. p. 22. ISBN 978-0-8493-8647-3。
32. Singal, S. (2005).騒音公害と制御戦略. オックスフォード: Alpha Science International. p. 7. ISBN 978-1-84265-237-4屈折効果は風の勾配がある場合にのみ発生し、音が風によって対流される結果によるものではないことがわかります。
33. Bies, David (2009). 『エンジニアリング騒音制御、理論と実践』 ロンドン: CRC Press. p. 249. ISBN 978-0-415-26713-7一般的に風速は高度とともに増加するため、音源から聞き手に向かって吹く風は音波を下方に屈折させ、結果として騒音レベルを上昇させます。
34. コーンウォール卿 (1996).グラントの軍事司令官としての立場. ニューヨーク: バーンズ・アンド・ノーブル. p. 92. ISBN 978-1-56619-913-1。
35. ピーター・コーゼンズ（2006年）『戦争の暗黒の日々：イウカとコリントスの戦い』チャペルヒル：ノースカロライナ大学出版局。ISBN 978-0-8078-5783-0。
36. AB Wood , A Textbook of Sound (Bell, London, 1946)
37. 「空気中の音速」 Phy.mtu.edu. 2017年6月23日時点のオリジナルよりアーカイブ。 2014年6月13日閲覧。
38. ザッカーワー著『実在気体中の音速ハンドブック』52ページ
39. J. Krautkrämer と H. Krautkrämer (1990)、「超音波材料試験」、第 4 版、Springer-Verlag、ベルリン、ドイツ、p. 497
40. Slade, Tyler; Anand, Shashwat; Wood, Max; Male, James; Imasato, Kazuki; Cheikh, Dean; Al Malki, Muath; Agne, Matthias; Griffith, Kent; Bux, Sabah; Wolverton, Chris; Kanatzidis, Mercouri; Snyder, Jeff (2021). 「電荷キャリア媒介格子軟化は熱電半導体の高zTに寄与する」 . Joule . 5 (5): 1168-1182. Bibcode : 2021Joule...5.1168S . doi : 10.1016/j.joule.2021.03.009 . S2CID 233598665 . 
41. , Jack Denman; Dolan, Dan (2025). 「超音波パルス受信機測定による固体の音速」 .サンディア国立研究所報告書. doi : 10.13140/RG.2.2.18031.50080 .
42. 「32～212°F（0～100°C）の温度における水中の音速 — ヤードポンド法とSI単位系」『エンジニアリングツールボックス』。
43. Wong, George SK; Zhu, Shi-ming (1995). 「海水中の音速と塩分濃度、温度、圧力の関係」アメリカ音響学会誌. 97 (3): 1732. Bibcode : 1995ASAJ...97.1732W . doi : 10.1121/1.413048 .
44. APL-UW TR 9407高周波海洋環境音響モデルハンドブック、pp. I1-I2。
45. Robinson, Stephen (2005年9月22日). 「技術ガイド – 海水中の音速」 .国立物理学研究所. 2017年4月29日時点のオリジナルよりアーカイブ。2016年12月7日閲覧。
46. 「音はどれくらい速く伝わるのか？」『海中の音の発見』ロードアイランド大学。2017年5月20日時点のオリジナルよりアーカイブ。 2010年11月30日閲覧。
47. Dushaw, Brian D.; Worcester, PF; Cornuelle, BD; Howe, BM (1993). 「海水中の音速に関する方程式について」. Journal of the Acoustical Society of America . 93 (1): 255– 275. Bibcode : 1993ASAJ...93..255D . doi : 10.1121/1.405660 .
48. Kenneth V., Mackenzie (1981). 「海水音速測定に関する考察」.アメリカ音響学会誌. 70 (3): 801– 806. Bibcode : 1981ASAJ...70..801M . doi : 10.1121/1.386919 .
49. Del Grosso, VA (1974). 「自然水中の音速に関する新しい式（他の式との比較を含む）」 . Journal of the Acoustical Society of America . 56 (4): 1084– 1091. Bibcode : 1974ASAJ...56.1084D . doi : 10.1121/1.1903388 .
50. マイネン, クリストファー・S.; ワッツ, D. ランドルフ (1997). 「デル・グロッソの音速アルゴリズムがチェンとミレロのアルゴリズムよりも正確であることを示すさらなる証拠」 .アメリカ音響学会誌. 102 (4): 2058– 2062. Bibcode : 1997ASAJ..102.2058M . doi : 10.1121/1.419655 . S2CID 38144335 . 
51. Maurice, S.; Chide, B.; Murdoch, N.; Lorenz, RD; Mimoun, D.; Wiens, RC; Stott, A.; Jacob, X.; Bertrand, T.; Montmessin, F.; Lanza, NL; Alvarez-Llamas, C.; Angel, SM; Aung, M.; Balaram, J. (2022年4月1日). 「火星のサウンドスケープの現場録音」 . Nature . 605 (7911): 653– 658. Bibcode : 2022Natur.605..653M . doi : 10.1038/s41586-022-04679-0 . ISSN 1476-4687 . PMC 9132769 . PMID 35364602。   

外部リンク

• 音速計算機
• 計算：空気中の音速と温度
• 音速：重要なのは気圧ではなく温度
• 1976年の米国標準大気の特性
• 音速
• 実験室で音速を測定する方法
• 音はかつて光速で伝わっていたのか？
• 音速を含む様々な材料の音響特性アーカイブ2014年2月16日 ウェイバックマシン
• 海における音の発見（人間や他の動物による音の利用）