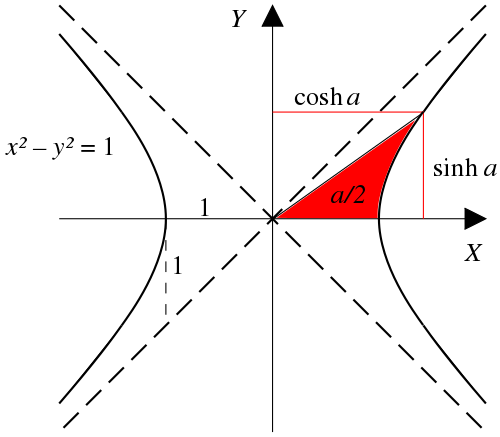
数学 において、双曲線関数は 通常の三角関数 に類似していますが、円 ではなく双曲線 を用いて定義されます。点(cos t , sin t ) が単位半径の円 を形成するのと同様に、点(cosh t , sinh t )は 単位双曲線 の右半分を形成します。また、 sin( t ) とcos( t ) の導関数がそれぞれcos( t ) と–sin( t ) であるのと同様に、 sinh( t ) とcosh( t ) の導関数はそれぞれcosh( t ) とsinh( t ) です。
双曲関数は、双曲幾何学 において平行角を 表すために使用されます。特殊相対論 では、ローレンツブーストを 双曲回転 として表すために使用されます。また、多くの線形微分方程式( 懸垂線 を定義する方程式など)、3次方程式 、および直交座標 におけるラプラス方程式 の解にも現れます。ラプラス方程式は、 電磁気学 、伝熱 、流体力学 など、物理学 の多くの分野で重要です。
基本的な双曲線関数は以下の通りである: [ 1 ]
そこから派生したもの: [ 4 ]
導出された三角関数に対応します。
逆双曲線関数は次の とおりです。
逆双曲線正弦 「arsinh 」(「sinh −1 」、「asinh 」、または「arcsinh 」と表記されることもある)[ 9 ] [ 10 ] [ 11 ] 逆双曲線余弦 「arcosh 」(「cosh −1 」、「acosh 」、または「arccosh 」と表記されることもある)逆双曲線正接 「artanh 」(「tanh −1 」、「atanh 」、または「arctanh 」と表記されることもある)逆双曲余接 「アークス」(「 アークス−1 」、「アークス 」、あるいは「アークス 」とも表記される)逆双曲正割 「arsech 」(「sech −1 」、「asech 」、または「arcsech 」と表記されることもある)逆双曲余割 「arcsch 」(「arcosech 」、「csch −1 」、「cosech −1 」、「acsch 」、「acosech 」、または「arccsch 」や「arccosech 」と表記されることもある)単位双曲線 x 2 − y 2 = 1 を通る直線が 点(cosh a , sinh a ) を通過する。ここでa は 直線、双曲線、x軸の間の面積の2倍である。x 軸より下の双曲線上の 点 については、面積は負とみなされる(三角関数(円関数)との比較を含むアニメーション版を 参照)。双曲関数は、双曲角 と呼ばれる引数 を取ります。双曲角の大きさは、xy = 1 に対する双曲扇形 の面積です。双曲関数は、この扇形を覆う 直角三角形の辺 によって定義できます。
複素解析 において、通常の正弦関数と余弦関数を虚角に適用すると双曲関数が生じる。双曲正弦関数と双曲余弦関数は整関数 である。その結果、他の双曲関数は複素平面全体において 有理型となる。
リンデマン・ワイエルシュトラスの定理 によれば、双曲関数は引数のゼロでない代数的値すべてに対して 超越値を持つ。 [ 12 ]
歴史 双曲三角法の問題の計算は、1566年頃にメルカトル図法を 発表したゲラルドゥス・メルカトルが初めて行ったとされています。この計算では、双曲関数を含む 超越方程式 の解を表にまとめる必要がありました。[ 13 ]
円の扇形と双曲線の扇形の類似性を最初に示唆したのは、アイザック・ニュートンが 1687年に著した『プリンキピア・マテマティカ』 [ 14 ]
ロジャー・コーツは、 虚数単位 を使って三角関数を修正し、長楕円体から扁平楕円体 を得ることを提案した。 [ 14 ] 私 = − 1 {\displaystyle i={\sqrt {-1}}}
双曲関数は1757年にヴィンチェンツォ・リカッティ によって正式に導入されました。[ 14 ] [ 13 ] [ 15 ] Sc. Cc. 正弦/余弦円 Sh. Ch. 正弦/余弦双曲)を使用しました。 [ 14 ] ダヴィエ・ド・フォンセネックスは 虚数単位を使用して三角関数と双曲関数の互換性を示し、ド・モアブルの公式を 双曲関数に拡張しました。[ 15 ] [ 14 ]
1760年代、ヨハン・ハインリヒ・ランベルトは 使用関数を体系化し、指数表現を様々な出版物で提供した。[ 14 ] [ 15 ] [ 15 ] [ 16 ]
表記
定義 sinhとcoshに比例する脚を持つ直角三角形 双曲線角 u では、双曲線関数 sinh と cosh は指数関数 e u で定義できます。[ 1 ] [ 4 ] あ = ( e − あなた 、 e あなた ) 、 B = ( e あなた 、 e − あなた ) 、 お あ + お B = お C {\displaystyle A=(e^{-u},e^{u}),\ B=(e^{u},\ e^{-u}),\ OA+OB=OC}
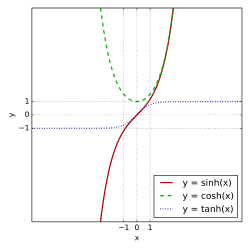
指数関数の定義 sinh xは e x e − x 差 の半分である。cosh xは e x e − x 平均 である。双曲線正弦:指数関数の奇数部 、つまりシン × = e × − e − × 2 = e 2 × − 1 2 e × 。 {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}.} 双曲線余弦:指数関数の偶数部 、つまりコッシュ × = e × + e − × 2 = e 2 × + 1 2 e × 。 {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}.} sinh 、cosh 、tanh csch 、sech 、coth 双曲線正接:タン × = シン × コッシュ × = e × − e − × e × + e − × = e 2 × − 1 e 2 × + 1 。 {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}。 双曲余接:x ≠0コス × = コッシュ × シン × = e × + e − × e × − e − × = e 2 × + 1 e 2 × − 1 。 {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}。 双曲正割:ゼック × = 1 コッシュ × = 2 e × + e − × = 2 e × e 2 × + 1 。 {\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}.} 双曲余割: x ≠ 0チェコ × = 1 シン × = 2 e × − e − × = 2 e × e 2 × − 1 。 {\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}.}
微分方程式の定義 双曲線関数は、微分方程式 の解として定義できます。双曲線正弦と双曲線余弦は、 初期条件を持つシステムの 解( s 、c ) です。初期条件により、解は一意になります。初期条件がなければ、どの関数のペアも解にはなりません。 c ′ ( × ) = s ( × ) 、 s ′ ( × ) = c ( × ) 、 {\displaystyle {\begin{aligned}c'(x)&=s(x),\\s'(x)&=c(x),\\\end{aligned}}} s ( 0 ) = 0 、 c ( 0 ) = 1. {\displaystyle s(0)=0,c(0)=1.} ( 1つの e × + b e − × 、 1つの e × − b e − × ) {\displaystyle (ae^{x}+be^{-x},ae^{x}-be^{-x})}
sinh( x ) とcosh( x ) は方程式f ″( x ) = f ( x )f (0) = 1f ′(0) = 0となり、双曲線正弦の場合はf (0) = 0f ′(0) = 1 となります
複雑な三角関数の定義 双曲線関数は、複素 引数を持つ三角関数 から推定することもできます。
双曲線正弦: [ 1 ] シン × = − 私 罪 ( 私 × ) 。 {\displaystyle \sinh x=-i\sin(ix).} 双曲線余弦: [ 1 ] コッシュ × = コス ( 私 × ) 。 {\displaystyle \cosh x=\cos(ix).} 双曲線正接:タン × = − 私 日焼け ( 私 × ) 。 {\displaystyle \tanh x=-i\tan(ix).} 双曲線余接:コス × = 私 ベビーベッド ( 私 × ) 。 {\displaystyle \coth x=i\cot(ix).} 双曲正割:ゼック × = 秒 ( 私 × ) 。 {\displaystyle \operatorname {sech} x=\sec(ix).} 双曲線余割:チェコ × = 私 csc ( 私 × ) 。 {\displaystyle \operatorname {csch} x=i\csc(ix).} ここで、i は虚数単位 で、i 2 = −1
上記の定義は、オイラーの公式 を介して指数定義と関連しています(以下の§複素数の双曲線関数を 参照)。
特性評価
双曲線余弦 双曲余弦曲線 の下の面積(有限区間にわたって)は常にその区間に対応する弧の長さ に等しいことが示される: [ 17 ] エリア = ∫ 1つの b コッシュ × d × = ∫ 1つの b 1 + ( d d × コッシュ × ) 2 d × = 弧の長さ。 {\displaystyle {\text{面積}}=\int _{a}^{b}\cosh x\,dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh x\right)^{2}}}\,dx={\text{弧の長さ}}}
双曲線正接 双曲正接は、微分方程式 f ′ = 1 − f 2 f (0) = 0 )[ 18 ] [ 19 ]
有用な関係 三角関数の恒等 式と形が似ています。実際、オズボーンの定理 [ 20 ] ジョージ・オズボーン にちなんで名付けられました)によれば、、、またはに対する任意の三角関数の恒等式(4次正弦および暗黙の正弦を除く)は、次のように双曲関数の恒等式に変換できます 。θ {\displaystyle \theta} 2 θ {\displaystyle 2\theta } 3 θ {\displaystyle 3\theta } θ {\displaystyle \theta} φ {\displaystyle \varphi }
これを正弦と余弦の積分乗で完全に拡張すると、 正弦をsinhに、余弦をcoshに変更し、 2 つの sinh の積を含むすべての項の符号を切り替えます。 奇数関数 と偶数 関数: シン ( − × ) = − シン × コッシュ ( − × ) = コッシュ × タン ( − × ) = − タン × コス ( − × ) = − コス × ゼック ( − × ) = ゼック × チェコ ( − × ) = − チェコ × {\displaystyle {\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\\\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\operatorname {csch} (-x)&=-\operatorname {csch} x\end{aligned}}}
逆数:
尻 × = アーコッシュ ( 1 × ) アークシュ × = アルシン ( 1 × ) アルコス × = アルタン ( 1 × ) {\displaystyle {\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} \left({\frac {1}{x}}\right)\\\operatorname {arcsch} x&=\operatorname {arsinh} \left({\frac {1}{x}}\right)\\\operatorname {arcoth} x&=\operatorname {artanh} \left({\frac {1}{x}}\right)\end{aligned}}}
オイラーの公式 に類似:
cosh x + sinh x = e x cosh x − sinh x = e − x {\displaystyle {\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\end{aligned}}}
ピタゴラスの三角関数の恒等式 に類似:
cosh 2 x − sinh 2 x = 1 1 − tanh 2 x = sech 2 x coth 2 x − 1 = csch 2 x {\displaystyle {\begin{aligned}\cosh ^{2}x-\sinh ^{2}x&=1\\1-\tanh ^{2}x&=\operatorname {sech} ^{2}x\\\coth ^{2}x-1&=\operatorname {csch} ^{2}x\end{aligned}}}
議論の和と差 sinh ( x + y ) = sinh x cosh y + cosh x sinh y cosh ( x + y ) = cosh x cosh y + sinh x sinh y tanh ( x + y ) = tanh x + tanh y 1 + tanh x tanh y sinh ( x − y ) = sinh x cosh y − cosh x sinh y cosh ( x − y ) = cosh x cosh y − sinh x sinh y tanh ( x − y ) = tanh x − tanh y 1 − tanh x tanh y {\displaystyle {\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x\sinh y\\\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\sinh(x-y)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(x-y)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(x-y)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{aligned}}} cosh ( 2 x ) = sinh 2 x + cosh 2 x = 2 sinh 2 x + 1 = 2 cosh 2 x − 1 sinh ( 2 x ) = 2 sinh x cosh x tanh ( 2 x ) = 2 tanh x 1 + tanh 2 x {\displaystyle {\begin{aligned}\cosh(2x)&=\sinh ^{2}{x}+\cosh ^{2}{x}=2\sinh ^{2}x+1=2\cosh ^{2}x-1\\\sinh(2x)&=2\sinh x\cosh x\\\tanh(2x)&={\frac {2\tanh x}{1+\tanh ^{2}x}}\\\end{aligned}}}
sinh x + sinh y = 2 sinh ( x + y 2 ) cosh ( x − y 2 ) cosh x + cosh y = 2 cosh ( x + y 2 ) cosh ( x − y 2 ) sinh x − sinh y = 2 cosh ( x + y 2 ) sinh ( x − y 2 ) cosh x − cosh y = 2 sinh ( x + y 2 ) sinh ( x − y 2 ) {\displaystyle {\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\sinh x-\sinh y&=2\cosh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {x-y}{2}}\right)\\\cosh x-\cosh y&=2\sinh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {x-y}{2}}\right)\\\end{aligned}}}
cosh x cosh y = 1 2 ( cosh ( x + y ) + cosh ( x − y ) ) sinh x sinh y = 1 2 ( cosh ( x + y ) − cosh ( x − y ) ) sinh x cosh y = 1 2 ( sinh ( x + y ) + sinh ( x − y ) ) cosh x sinh y = 1 2 ( sinh ( x + y ) − sinh ( x − y ) ) {\displaystyle {\begin{aligned}\cosh x\,\cosh y&={\tfrac {1}{2}}{\bigl (}\!\!~\cosh(x+y)+\cosh(x-y){\bigr )}\\[5mu]\sinh x\,\sinh y&={\tfrac {1}{2}}{\bigl (}\!\!~\cosh(x+y)-\cosh(x-y){\bigr )}\\[5mu]\sinh x\,\cosh y&={\tfrac {1}{2}}{\bigl (}\!\!~\sinh(x+y)+\sinh(x-y){\bigr )}\\[5mu]\cosh x\,\sinh y&={\tfrac {1}{2}}{\bigl (}\!\!~\sinh(x+y)-\sinh(x-y){\bigr )}\\[5mu]\end{aligned}}}
sinh ( x 2 ) = sinh x 2 ( cosh x + 1 ) = sgn x cosh x − 1 2 cosh ( x 2 ) = cosh x + 1 2 tanh ( x 2 ) = sinh x cosh x + 1 = sgn x cosh x − 1 cosh x + 1 = e x − 1 e x + 1 {\displaystyle {\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)}}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}}\right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{aligned}}}
ここで、sgnは 符号関数 です。
x ≠ 0
tanh ( x 2 ) = cosh x − 1 sinh x = coth x − csch x {\displaystyle \tanh \left({\frac {x}{2}}\right)={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x}
t = tanh ( x 2 ) {\displaystyle t=\tanh \left({\frac {x}{2}}\right)} 、 sinh x = 2 t 1 − t 2 , cosh x = 1 + t 2 1 − t 2 , tanh x = 2 t 1 + t 2 , coth x = 1 + t 2 2 t , sech x = 1 − t 2 1 + t 2 , csch x = 1 − t 2 2 t . {\displaystyle {\begin{aligned}&\sinh x={\frac {2t}{1-t^{2}}},&&\cosh x={\frac {1+t^{2}}{1-t^{2}}},\\[8pt]&\tanh x={\frac {2t}{1+t^{2}}},&&\coth x={\frac {1+t^{2}}{2t}},\\[8pt]&\operatorname {sech} x={\frac {1-t^{2}}{1+t^{2}}},&&\operatorname {csch} x={\frac {1-t^{2}}{2t}}.\end{aligned}}}
sinh 2 x = 1 2 ( cosh 2 x − 1 ) cosh 2 x = 1 2 ( cosh 2 x + 1 ) {\displaystyle {\begin{aligned}\sinh ^{2}x&={\tfrac {1}{2}}(\cosh 2x-1)\\\cosh ^{2}x&={\tfrac {1}{2}}(\cosh 2x+1)\end{aligned}}}
不平等 次の不等式は統計学で有用である: [ 21 ] cosh ( t ) ≤ e t 2 / 2 . {\displaystyle \operatorname {cosh} (t)\leq e^{t^{2}/2}.}
これは、2 つの関数のテイラー級数を各項ごとに比較することによって証明できます。
逆関数を対数として表す arsinh ( x ) = ln ( x + x 2 + 1 ) arcosh ( x ) = ln ( x + x 2 − 1 ) x ≥ 1 artanh ( x ) = 1 2 ln ( 1 + x 1 − x ) | x | < 1 arcoth ( x ) = 1 2 ln ( x + 1 x − 1 ) | x | > 1 arsech ( x ) = ln ( 1 x + 1 x 2 − 1 ) = ln ( 1 + 1 − x 2 x ) 0 < x ≤ 1 arcsch ( x ) = ln ( 1 x + 1 x 2 + 1 ) x ≠ 0 {\displaystyle {\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x)&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&&x\geq 1\\\operatorname {artanh} (x)&={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)&&|x|<1\\\operatorname {arcoth} (x)&={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)&&|x|>1\\\operatorname {arsech} (x)&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)&&0<x\leq 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)&&x\neq 0\end{aligned}}}
デリバティブ d d x sinh x = cosh x d d x cosh x = sinh x d d x tanh x = 1 − tanh 2 x = sech 2 x = 1 cosh 2 x d d x coth x = 1 − coth 2 x = − csch 2 x = − 1 sinh 2 x x ≠ 0 d d x sech x = − tanh x sech x d d x csch x = − coth x csch x x ≠ 0 {\displaystyle {\begin{aligned}{\frac {d}{dx}}\sinh x&=\cosh x\\{\frac {d}{dx}}\cosh x&=\sinh x\\{\frac {d}{dx}}\tanh x&=1-\tanh ^{2}x=\operatorname {sech} ^{2}x={\frac {1}{\cosh ^{2}x}}\\{\frac {d}{dx}}\coth x&=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-{\frac {1}{\sinh ^{2}x}}&&x\neq 0\\{\frac {d}{dx}}\operatorname {sech} x&=-\tanh x\operatorname {sech} x\\{\frac {d}{dx}}\operatorname {csch} x&=-\coth x\operatorname {csch} x&&x\neq 0\end{aligned}}} d d x arsinh x = 1 x 2 + 1 d d x arcosh x = 1 x 2 − 1 1 < x d d x artanh x = 1 1 − x 2 | x | < 1 d d x arcoth x = 1 1 − x 2 1 < | x | d d x arsech x = − 1 x 1 − x 2 0 < x < 1 d d x arcsch x = − 1 | x | 1 + x 2 x ≠ 0 {\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&={\frac {1}{\sqrt {x^{2}+1}}}\\{\frac {d}{dx}}\operatorname {arcosh} x&={\frac {1}{\sqrt {x^{2}-1}}}&&1<x\\{\frac {d}{dx}}\operatorname {artanh} x&={\frac {1}{1-x^{2}}}&&|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&={\frac {1}{1-x^{2}}}&&1<|x|\\{\frac {d}{dx}}\operatorname {arsech} x&=-{\frac {1}{x{\sqrt {1-x^{2}}}}}&&0<x<1\\{\frac {d}{dx}}\operatorname {arcsch} x&=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}&&x\neq 0\end{aligned}}}
2次導関数 各関数sinh とcosh はその 2 次導関数 に等しくなります。つまり、次のようになります。 d 2 d x 2 sinh x = sinh x {\displaystyle {\frac {d^{2}}{dx^{2}}}\sinh x=\sinh x} d 2 d x 2 cosh x = cosh x . {\displaystyle {\frac {d^{2}}{dx^{2}}}\cosh x=\cosh x\,.}
この性質を持つ関数はすべてsinh とcosh の線形結合 であり、特に指数関数 とがそうである。[ 22 ] e x {\displaystyle e^{x}} e − x {\displaystyle e^{-x}}
標準積分 ∫ sinh ( a x ) d x = a − 1 cosh ( a x ) + C ∫ cosh ( a x ) d x = a − 1 sinh ( a x ) + C ∫ tanh ( a x ) d x = a − 1 ln ( cosh ( a x ) ) + C ∫ coth ( a x ) d x = a − 1 ln | sinh ( a x ) | + C ∫ sech ( a x ) d x = a − 1 arctan ( sinh ( a x ) ) + C ∫ csch ( a x ) d x = a − 1 ln | tanh ( a x 2 ) | + C = a − 1 ln | coth ( a x ) − csch ( a x ) | + C = − a − 1 arcoth ( cosh ( a x ) ) + C {\displaystyle {\begin{aligned}\int \sinh(ax)\,dx&=a^{-1}\cosh(ax)+C\\\int \cosh(ax)\,dx&=a^{-1}\sinh(ax)+C\\\int \tanh(ax)\,dx&=a^{-1}\ln(\cosh(ax))+C\\\int \coth(ax)\,dx&=a^{-1}\ln \left|\sinh(ax)\right|+C\\\int \operatorname {sech} (ax)\,dx&=a^{-1}\arctan(\sinh(ax))+C\\\int \operatorname {csch} (ax)\,dx&=a^{-1}\ln \left|\tanh \left({\frac {ax}{2}}\right)\right|+C=a^{-1}\ln \left|\coth \left(ax\right)-\operatorname {csch} \left(ax\right)\right|+C=-a^{-1}\operatorname {arcoth} \left(\cosh \left(ax\right)\right)+C\end{aligned}}}
次の積分は双曲置換法 を使って証明できます。 ∫ 1 a 2 + u 2 d u = arsinh ( u a ) + C ∫ 1 u 2 − a 2 d u = sgn u arcosh | u a | + C ∫ 1 a 2 − u 2 d u = a − 1 artanh ( u a ) + C u 2 < a 2 ∫ 1 a 2 − u 2 d u = a − 1 arcoth ( u a ) + C u 2 > a 2 ∫ 1 u a 2 − u 2 d u = − a − 1 arsech | u a | + C ∫ 1 u a 2 + u 2 d u = − a − 1 arcsch | u a | + C {\displaystyle {\begin{aligned}\int {{\frac {1}{\sqrt {a^{2}+u^{2}}}}\,du}&=\operatorname {arsinh} \left({\frac {u}{a}}\right)+C\\\int {{\frac {1}{\sqrt {u^{2}-a^{2}}}}\,du}&=\operatorname {sgn} {u}\operatorname {arcosh} \left|{\frac {u}{a}}\right|+C\\\int {\frac {1}{a^{2}-u^{2}}}\,du&=a^{-1}\operatorname {artanh} \left({\frac {u}{a}}\right)+C&&u^{2}<a^{2}\\\int {\frac {1}{a^{2}-u^{2}}}\,du&=a^{-1}\operatorname {arcoth} \left({\frac {u}{a}}\right)+C&&u^{2}>a^{2}\\\int {{\frac {1}{u{\sqrt {a^{2}-u^{2}}}}}\,du}&=-a^{-1}\operatorname {arsech} \left|{\frac {u}{a}}\right|+C\\\int {{\frac {1}{u{\sqrt {a^{2}+u^{2}}}}}\,du}&=-a^{-1}\operatorname {arcsch} \left|{\frac {u}{a}}\right|+C\end{aligned}}}
ここで、Cは 積分定数 です。
テイラー級数表現 上記の関数のゼロにおけるテイラー級数 (関数がゼロで定義されていない場合は ローラン級数 )を明示的に表現することができます。
sinh x = x + x 3 3 ! + x 5 5 ! + x 7 7 ! + ⋯ = ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}} xの任意の 複素数 値に対して収束します 。関数sinh x は奇数 なので、テイラー級数に はx
cosh x = 1 + x 2 2 ! + x 4 4 ! + x 6 6 ! + ⋯ = ∑ n = 0 ∞ x 2 n ( 2 n ) ! {\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}} xの任意の 複素数 値に対して収束します 。関数cosh x は 偶数 なので、テイラー級数には x の偶数指数のみが含まれます。
sinh 級数と cosh 級数の和は、指数関数 の無限級数 表現です。
次の級数の後には、その収束領域 のサブセットの説明が続きます。ここで、級数は収束し、その和は関数に等しくなります。 tanh x = x − x 3 3 + 2 x 5 15 − 17 x 7 315 + ⋯ = ∑ n = 1 ∞ 2 2 n ( 2 2 n − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! , | x | < π 2 coth x = x − 1 + x 3 − x 3 45 + 2 x 5 945 + ⋯ = ∑ n = 0 ∞ 2 2 n B 2 n x 2 n − 1 ( 2 n ) ! , 0 < | x | < π sech x = 1 − x 2 2 + 5 x 4 24 − 61 x 6 720 + ⋯ = ∑ n = 0 ∞ E 2 n x 2 n ( 2 n ) ! , | x | < π 2 csch x = x − 1 − x 6 + 7 x 3 360 − 31 x 5 15120 + ⋯ = ∑ n = 0 ∞ 2 ( 1 − 2 2 n − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! , 0 < | x | < π {\displaystyle {\begin{aligned}\tanh x&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\qquad \left|x\right|<{\frac {\pi }{2}}\\\coth x&=x^{-1}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots =\sum _{n=0}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},\qquad 0<\left|x\right|<\pi \\\operatorname {sech} x&=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\qquad \left|x\right|<{\frac {\pi }{2}}\\\operatorname {csch} x&=x^{-1}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots =\sum _{n=0}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},\qquad 0<\left|x\right|<\pi \end{aligned}}}
どこ:
B n {\displaystyle B_{n}} n 番目のベルヌーイ数 であるE n {\displaystyle E_{n}} n 番目のオイラー数 である
無限積と連分数 複素平面全体では次のような展開が有効です。
sinh x = x ∏ n = 1 ∞ ( 1 + x 2 n 2 π 2 ) = x 1 − x 2 2 ⋅ 3 + x 2 − 2 ⋅ 3 x 2 4 ⋅ 5 + x 2 − 4 ⋅ 5 x 2 6 ⋅ 7 + x 2 − ⋱ {\displaystyle \sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{n^{2}\pi ^{2}}}\right)={\cfrac {x}{1-{\cfrac {x^{2}}{2\cdot 3+x^{2}-{\cfrac {2\cdot 3x^{2}}{4\cdot 5+x^{2}-{\cfrac {4\cdot 5x^{2}}{6\cdot 7+x^{2}-\ddots }}}}}}}}} cosh x = ∏ n = 1 ∞ ( 1 + x 2 ( n − 1 / 2 ) 2 π 2 ) = 1 1 − x 2 1 ⋅ 2 + x 2 − 1 ⋅ 2 x 2 3 ⋅ 4 + x 2 − 3 ⋅ 4 x 2 5 ⋅ 6 + x 2 − ⋱ {\displaystyle \cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{(n-1/2)^{2}\pi ^{2}}}\right)={\cfrac {1}{1-{\cfrac {x^{2}}{1\cdot 2+x^{2}-{\cfrac {1\cdot 2x^{2}}{3\cdot 4+x^{2}-{\cfrac {3\cdot 4x^{2}}{5\cdot 6+x^{2}-\ddots }}}}}}}}} tanh x = 1 1 x + 1 3 x + 1 5 x + 1 7 x + ⋱ {\displaystyle \tanh x={\cfrac {1}{{\cfrac {1}{x}}+{\cfrac {1}{{\cfrac {3}{x}}+{\cfrac {1}{{\cfrac {5}{x}}+{\cfrac {1}{{\cfrac {7}{x}}+\ddots }}}}}}}}}
円関数との比較 (1, 1) における円と双曲線の接線は、円弧面積 uに 基づく円関数と、双曲線 面積u に依存する双曲線関数の幾何学を表示します。双曲線関数は、円関数を 超えた三角法 の拡張を表します。どちらの関数も、円角 または双曲線角のいずれかの 引数 に依存します。
半径r 、角度u (ラジアン)の扇形の面積は r 2 u / 2なので、 r = √ 2 u と等しくなります。図では、このような円は(1, 1) において双曲線xy = 1 に接しています。黄色の扇形は面積と角度の大きさを表しています。同様に、黄色と赤色の領域は、面積が双曲線の角度の大きさに対応する 双曲扇形 を表しています。
角度を定義する放射状の斜辺 を持つ2 つの直角三角形 の脚の長さは、円関数と双曲線関数 の√ 2倍です。
双曲角は、円角が回転に対して不変であるのと同様に、スクイーズ写像 に関して不変の測度 である。[ 23 ]
グーデルマン関数は 、複素数を含まない円関数と双曲線関数の間の直接的な関係を与えます。
関数 のグラフはa cosh ( x / a ) {\displaystyle a\cosh(x/a)} 懸垂線 、つまり均一な重力下にある 2 つの固定点の間に自由に垂れ下がった均一で柔軟な鎖によって形成される曲線 です。
指数関数との関係 指数関数を偶数部と奇数部 に分解すると、恒等式とが得られます。 これを オイラーの公式 と組み合わせると、 一般 的な複素指数関数 が得られ ます。 e x = cosh x + sinh x , {\displaystyle e^{x}=\cosh x+\sinh x,} e − x = cosh x − sinh x . {\displaystyle e^{-x}=\cosh x-\sinh x.} e i x = cos x + i sin x , {\displaystyle e^{ix}=\cos x+i\sin x,} e x + i y = ( cosh x + sinh x ) ( cos y + i sin y ) {\displaystyle e^{x+iy}=(\cosh x+\sinh x)(\cos y+i\sin y)}
さらに、 e x = 1 + tanh x 1 − tanh x = 1 + tanh x 2 1 − tanh x 2 {\displaystyle e^{x}={\sqrt {\frac {1+\tanh x}{1-\tanh x}}}={\frac {1+\tanh {\frac {x}{2}}}{1-\tanh {\frac {x}{2}}}}}
複素数の双曲線関数 複素平面上の双曲線関数 sinh ( z ) {\displaystyle \sinh(z)} cosh ( z ) {\displaystyle \cosh(z)} tanh ( z ) {\displaystyle \tanh(z)} coth ( z ) {\displaystyle \coth(z)} sech ( z ) {\displaystyle \operatorname {sech} (z)} csch ( z ) {\displaystyle \operatorname {csch} (z)}
指数関数は任意 の複素 引数に対して定義できるため、双曲関数の定義を複素引数に拡張することもできます。この場合、関数sinh z とcosh z は正則関数と なります。
通常の三角関数との関係は、複素数の オイラーの公式 によって与えられます。 つまり、 e i x = cos x + i sin x e − i x = cos x − i sin x {\displaystyle {\begin{aligned}e^{ix}&=\cos x+i\sin x\\e^{-ix}&=\cos x-i\sin x\end{aligned}}} cosh ( i x ) = 1 2 ( e i x + e − i x ) = cos x sinh ( i x ) = 1 2 ( e i x − e − i x ) = i sin x tanh ( i x ) = i tan x cosh ( x + i y ) = cosh ( x ) cos ( y ) + i sinh ( x ) sin ( y ) sinh ( x + i y ) = sinh ( x ) cos ( y ) + i cosh ( x ) sin ( y ) tanh ( x + i y ) = tanh ( x ) + i tan ( y ) 1 + i tanh ( x ) tan ( y ) cosh x = cos ( i x ) sinh x = − i sin ( i x ) tanh x = − i tan ( i x ) {\displaystyle {\begin{aligned}\cosh(ix)&={\frac {1}{2}}\left(e^{ix}+e^{-ix}\right)=\cos x\\\sinh(ix)&={\frac {1}{2}}\left(e^{ix}-e^{-ix}\right)=i\sin x\\\tanh(ix)&=i\tan x\\\cosh(x+iy)&=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\\\sinh(x+iy)&=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\\\tanh(x+iy)&={\frac {\tanh(x)+i\tan(y)}{1+i\tanh(x)\tan(y)}}\\\cosh x&=\cos(ix)\\\sinh x&=-i\sin(ix)\\\tanh x&=-i\tan(ix)\end{aligned}}}
したがって、双曲線関数は虚数成分に関して周期的で あり、周期は(双曲線正接と双曲線余接の場合)です。 2 π i {\displaystyle 2\pi i} π i {\displaystyle \pi i}
参照
参考文献 ^ a b c d Weisstein, Eric W. 「双曲関数」 . mathworld.wolfram.com . 2020年8月29日 閲覧 。^ (1999)コリンズ・コンサイス辞典 、第4版、ハーパーコリンズ、グラスゴー、 ISBN 0 00 472257 4 ^ a b コリンズコンサイス辞典 、328ページ^ a b 「双曲線関数」 www.mathsisfun.com . 2020年8月29日 閲覧 。 ^ コリンズ・コンサイス辞典 、1520ページ^ コリンズ・コンサイス辞典 、329ページ^ tanh ^ コリンズ・コンサイス辞典 、1340ページ^ Woodhouse, NMJ (2003), Special Relativity , London: Springer, p. 71, ISBN 978-1-85233-426-0 ^ アブラモウィッツ、ミルトン 、 ステガン 、アイリーンA.編(1972年)、 数式、グラフ、数学表付き数学関数ハンドブック 、ニューヨーク: ドーバー出版 、 ISBN 978-0-486-61272-0 ^ arcsinh の使用例が Google ブックス で見つかりました。^ ニーヴン、イヴァン(1985年) 『無理数 』第11巻、アメリカ数学会 ISBN 9780883850381 JSTOR 10.4169/j.ctt5hh8zn .^ a b George F. Becker; CE Van Orstrand (1909). 双曲関数 . ユニバーサルデジタルライブラリ. スミソニアン協会. ^ a b c d e f マクマホン、ジェームズ (1896). 双曲関数 . オスマニア大学、インドデジタル図書館. ジョン・ワイリー・アンド・サンズ. ^ a b c d ブラッドリー, ロバート・E.、ダントニオ, ローレンス・A.、サンディファー, チャールズ・エドワード.オイラー生誕300年:その意義. アメリカ数学会, 2007年. 100ページ. ^ ベッカー、ゲオルグ・F.双曲関数. リードブックス, 1931年. xlviiiページ. ^ NP, Bali (2005). Golden Integral Calculus . Firewall Media. p. 472. ISBN 81-7008-169-6 ^ Steeb, Willi-Hans (2005). 『非線形ワークブック:カオス、フラクタル、セルオートマトン、ニューラルネットワーク、遺伝的アルゴリズム、遺伝子発現プログラミング、サポートベクターマシン、ウェーブレット、隠れマルコフモデル、ファジーロジック(C++、Java、SymbolicC++プログラムによる)』 (第3版). World Scientific Publishing Company. p. 281. ISBN 978-981-310-648-2 281ページの抜粋(lambda=1を使用) ^ オールドハム, キース・B.; マイランド, ヤン; スパニアー, ジェローム (2010). 『関数アトラス:アトラス関数計算機 Equator (第2版、イラスト入り)』 Springer Science & Business Media. p. 290. ISBN 978-0-387-48807-3 290ページの抜粋 ^ Osborn, G. (1902年7月 ). 「双曲型公式の記憶法」 . The Mathematical Gazette . 2 (34): 189. doi : 10.2307/3602492 . JSTOR 3602492. S2CID 125866575 . ^ Audibert, Jean-Yves (2009). 「集約による統計的推論における高速学習率」『統計年報』1627頁。 [1] ^ Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. 編 (2010) 「双曲関数」 、 NIST Handbook of Mathematical Functions 、ケンブリッジ大学出版局、 ISBN 978-0-521-19225-5 MR 2723248 ^ Haskell, Mellen W. 、「双曲関数の概念の導入について」、 アメリカ数学会報 1 :6:155–9、全文
外部リンク 








































![{\displaystyle {\begin{aligned}\cosh x\,\cosh y&={\tfrac {1}{2}}{\bigl (}\!\!~\cosh(x+y)+\cosh(xy){\bigr )}\\[5mu]\sinh x\,\sinh y&={\tfrac {1}{2}}{\bigl (}\!\!~\cosh(x+y)-\cosh(xy){\bigr )}\\[5mu]\sinh x\,\cosh y&={\tfrac {1}{2}}{\bigl (}\!\!~\sinh(x+y)+\sinh(xy){\bigr )}\\[5mu]\cosh x\,\sinh y&={\tfrac {1}{2}}{\bigl (}\!\!~\sinh(x+y)-\sinh(xy){\bigr )}\\[5mu]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebcc6e905df736163061cf56b304ab50d7853739)
![{\displaystyle {\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)}}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}}\right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/412a4ffd109486f684e515634b33447b13444954)


![{\displaystyle {\begin{aligned}&\sinh x={\frac {2t}{1-t^{2}}},&&\cosh x={\frac {1+t^{2}}{1-t^{2}}},\\[8pt]&\tanh x={\frac {2t}{1+t^{2}}},&&\coth x={\frac {1+t^{2}}{2t}},\\[8pt]&\operatorname {sech} x={\frac {1-t^{2}}{1+t^{2}}},&&\operatorname {csch} x={\frac {1-t^{2}}{2t}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c5e6413116e81cae13055fdf64801ff32f597a5)



































