スチューデントのt検定

スチューデントのt検定は、2 つのグループの応答の差が統計的に有意かどうかを検定するために使用される統計的検定です。これは、帰無仮説の下で検定統計量がスチューデントのt分布に従う統計的仮説検定です。検定統計量のスケーリング項の値が既知である場合に検定統計量が正規分布に従うときに最も一般的に適用されます(通常、スケーリング項は未知であるため、不要なパラメーター)。スケーリング項がデータに基づいて推定される場合、検定統計量は (特定の条件下では) スチューデントのt分布に従います。t検定の最も一般的な用途は、2 つの母集団の平均が有意に異なるかどうかを検定することです。多くの場合、データ セットのサイズが大きくなるにつれて、後者は前者に収束するため 、 Z検定はt検定と非常によく似た結果になります。

歴史

ウィリアム・シーリー・ゴセットは「t統計量」を開発し、 「学生」という偽名で出版した。

「 t統計量」という用語は、「仮説検定統計量」の略です。^{[ 1 ]}統計学において、t分布は1876 年にHelmert ^{[ 2 ] [ 3 ] [ 4 ]}とLürothによって事後分布として初めて導き出されました。^{[ 5 ] [ 6 ] [ 7 ]} t分布は、 Karl Pearsonの 1895 年の論文で、より一般的な形の Pearson type  IV分布としても登場しました。 ^{[ 8 ]}しかし、スチューデントのt分布としても知られるt分布の名前は、William Sealy Gossetに由来します。彼は、1908 年に科学雑誌Biometrikaに「Student」というペンネームを使用して英語で初めてこの分布を発表しましたが、これは^{、彼の雇用主が、}科学論文を発表する際にはスタッフにペンネームを使用することを好んだ^ためです。^{[ 10 ]}ゴセットはアイルランドのダブリンにあるギネス醸造所で働き、少量サンプルの問題、例えば少量サンプルでの大麦の化学的性質などに興味を持っていました。そのため、「Student」という用語の語源の2つ目の説は、ギネスが競合他社にt検定を用いて原材料の品質を判断していることを知られたくなかったというものです。「Student」という用語はウィリアム・ゴセットにちなんで造られましたが、実際にはロナルド・フィッシャーの研究によって、この分布は「スチューデント分布」 ^{[ 11 ]}や「スチューデントのt検定」としてよく知られるようになりました。

ゴセットはスタウトの品質を経済的な方法で監視するためにt検定を考案しました。このt検定の研究はBiometrika誌に投稿され、受理され、1908年に出版されました^{。[ 9 ]}

ギネスには技術職員に研究休暇（いわゆる「研究休暇」）を認める方針があり、ゴセットは1906年から1907年の最初の2学期にロンドン大学ユニバーシティ・カレッジのカール・ピアソン教授の生体測定学研究所でこの休暇を利用した。^{[ 12 ]}ゴセットの身元は当時、同僚の統計学者や編集長のカール・ピアソンに知られていた。^{[ 13 ]}

用途

1標本t検定

1標本スチューデントのt検定は、母集団の平均が帰無仮説で指定された値を持つかどうかを検定する位置検定である。母集団の平均が指定された値μ ₀に等しいという帰無仮説を検定する際には、統計量を用いる。

${\displaystyle t={\frac {{\bar {x}}-\mu _{0}}{s/{\sqrt {n}}}},}$

ここで、 は標本平均、sは標本標準偏差、nは標本サイズです。この検定で使用される自由度はn  − 1です。母集団が正規分布している必要はありませんが、標本平均の母集団の分布は正規分布していると仮定します。 ${\displaystyle {\bar {x}}}$ ${\displaystyle {\bar {x}}}$

中心極限定理によれば、観測値が独立で2次モーメントが存在する場合、 はほぼ正規分布 となる。これは近似値に過ぎない。中心極限定理は、s がxの実際の標準偏差であればtにも適用されるが、実際の標準偏差は一般には不明であるため、 s は標本標準偏差となる。したがって、t は漸近的にスチューデントのt分布に従う。 ${\displaystyle t}$ ${\textstyle {\mathcal {N}}(0,1)}$

2標本t検定

相関の関数としての、対応のない2標本t検定と対応のある2標本t検定のタイプI誤差。シミュレートされた乱数は、分散1の2変量正規分布から生成されます。有意水準は5%、症例数は60です。

相関の関数としての、対応のない2標本t検定と対応のある2標本t検定の検出力。シミュレートされた乱数は、分散1、期待値の偏差0.4の2変量正規分布から生成されます。有意水準は5%、事例数は60です。

2つの母集団の平均が等しいという帰無仮説の2標本位置検定。このような検定はすべて通常スチューデントのt検定と呼ばれるが、厳密に言えば、この名称は2つの母集団の分散も等しいと仮定した場合にのみ用いられるべきである。この仮定を放棄した検定形式は、ウェルチのt検定と呼ばれることもある。これらの検定は、比較対象となる2つの標本の統計単位が重複していない場合に典型的に適用されるため、しばしば無対標本t検定または独立標本 t検定と呼ばれる。^{[ 14 ]}

平均値の差を調べる2標本t検定では、独立標本（無対標本）または対標本を用いる。対t検定はブロッキング検定の一種であり、比較対象となる2つのグループの所属とは無関係な「ノイズ因子」（交絡因子を参照）に関して、対の単位が類似している場合、対でない検定よりも高い検出力（偽陰性とも呼ばれる第2種の誤りを回避する確率）を持つ。^{[ 15 ]}別の文脈では、対t検定は観察研究において交絡因子の影響を軽減するために用いられる。

独立（非対応）サンプル

独立標本t検定は、独立かつ同一分布の標本を2組取得し、それぞれの母集団から1つの変数を比較する場合に用いられます。例えば、ある医療処置の効果を評価するために、100人の被験者を研究に登録し、50人を処置群、50人を対照群に無作為に割り付けるとします。この場合、2つの独立標本が得られるため、対応のないt検定を使用します。

ペアサンプル

対応のあるサンプルのt検定は、通常、類似の単位の対応するペアのサンプル、または 2 回テストされた単位の 1 つのグループ (「反復測定」t検定) で構成されます。

反復測定t検定の典型的な例としては、被験者を高血圧などの治療前に検査し、血圧降下剤による治療後に同じ被験者を再度検査する場合が挙げられます。治療前後の同じ患者の数値を比較することで、各患者を実質的に対照群として用いていることになります。こうすることで、帰無仮説（ここでは治療による差がないという仮説）を正しく棄却できる可能性が大幅に高まり、患者間のランダムな変動が排除されるため、統計的検出力が向上します。しかし、統計的検出力の向上には代償が伴います。より多くの検査が必要となり、各被験者を2回検査する必要があるのです。

サンプルの半分がもう半分に依存しているため、スチューデントのt検定の対応のあるバージョンでは、⁠n/2⁠ − 1 の自由度（ nは観測値の総数）。ペアは個別の検定単位となり、同じ自由度数を達成するには標本を2倍にする必要がある。通常、自由度はn − 1である（ nは観測値の総数）。 ^{[ 16 ]}

「対応のあるサンプル」に基づく対応のあるサンプルのt検定は、対応のないサンプルから得られた結果であり、その後、対象変数と共に測定された追加変数を用いて対応のあるサンプルを形成するために使用される。^{[ 17 ]}対応付けは、2つのサンプルのそれぞれから1つの観測値からなる値のペアを特定することによって行われる。このペアは、他の測定変数に関して類似している。このアプローチは、交絡因子の影響を軽減または排除するために、観察研究において時々使用される。

対応のあるサンプルのt検定は、多くの場合、「従属サンプルのt検定」と呼ばれます。

仮定

ほとんどの検定統計量はt = Z / sという形式をとります。ここで、Zとs はデータの関数です。

Z は対立仮説に敏感である可能性があります (つまり、対立仮説が正しい場合はその大きさが大きくなる傾向があります)。一方、 sはtの分布を決定できるようにするスケーリング パラメーターです。

例えば、1標本t検定 では

${\displaystyle t={\frac {Z}{s}}={\frac {{\bar {X}}-\mu }{{\hat {\sigma }}/{\sqrt {n}}}},}$

ここで、 はサイズnの標本X ₁、X ₂、…、X _nからの標本平均、sは平均の標準誤差、は母集団の標準偏差の推定値、 μは母平均です。 ${\displaystyle {\bar {X}}}$ ${\displaystyle {\hat {\sigma }}={\sqrt {{\frac {1}{n-1}}\sum _{i}(X_{i}-{\bar {X}})^{2}}}}$

上記の最も単純な形式の t検定の基礎となる仮定は次のとおりです。

• Xは平均μと分散σ2 ^/ nの正規分布に従います。
• s ² ( n  − 1)/ σ ²は自由度n  − 1のχ ²分布に従う。この仮定は、 s ^{2 の}推定に用いられる観測値が正規分布（および各グループについてiid）に従う場合に満たされる。
• Zとsは独立しています。

2 つの独立したサンプルの平均を比較する t検定では、次の仮定を満たす必要があります。

• 比較対象となる2つの母集団の平均は正規分布に従うべきである。弱い仮定の下では、たとえ各グループの観測値の分布が非正規であっても、大規模な標本においては中心極限定理からこのことが導かれる。^{[ 18 ]}
• スチューデントによるt検定の本来の定義を使用する場合、比較される2つの母集団は同じ分散を持つ必要があります（F検定、レヴィン検定、バートレット検定、またはブラウン・フォーサイス検定を使用して検定可能、またはQ-Qプロットを使用してグラフで評価可能）。比較される2つのグループの標本サイズが等しい場合、スチューデントによる本来の定義のt検定は、不等分散の存在に対して非常に堅牢です。^{[ 19 ]}ウェルチのt検定は、標本サイズが類似しているかどうかに関わらず、分散の等分散性には鈍感です。
• 検定に用いるデータは、比較対象となる2つの母集団から独立してサンプリングするか、完全に対応のあるデータでなければならない。これは一般的にデータから検定することはできないが、データが従属関係にあることが分かっている場合（例えば、検定設計によって対応関係にある場合）、従属検定を適用する必要がある。部分的に対応のあるデータの場合、従来の独立t検定では検定統計量がt分布に従わない可能性があるため、無効な結果となる可能性がある。一方、従属t検定は対応のないデータを除外するため、最適ではない。^{[ 20 ]}

ほとんどの2標本t検定は、仮定からの大きな逸脱を除いて、すべてに対して堅牢である。^{[ 21 ]}

正確性のために、t検定とZ検定では標本平均値が正規性を持つことが必要であり、t検定ではさらに標本分散が尺度付きχ2分布に従うことと、標本平均値と標本分散が統計的に独立して^いることが必要である。これらの条件が満たされる場合、個々のデータ値の正規性は要求されない。中心極限定理により、中程度の大きさの標本の標本平均値は、データが正規分布していなくても、正規分布によって十分に近似されることが多い。しかし、標本平均値が正規分布に収束するために必要な標本サイズは、元データの分布の歪度に依​​存する。標本サイズは歪度に応じて30から100、あるいはそれ以上の値になることがある。^{[ 22 ] [ 23 ]}

非正規データの場合、標本分散の分布はχ ²分布から大幅に逸脱する可能性があります。

しかし、標本サイズが大きい場合、スラツキーの定理によれば、標本分散の分布は検定統計量の分布にほとんど影響を与えない。つまり、標本サイズが大きくなるにつれて、以下のようになる。 ${\displaystyle n}$

${\displaystyle {\sqrt {n}}({\bar {X}}-\mu )\xrightarrow {d} N(0,\sigma ^{2})}$ 中心極限定理によれば、

${\displaystyle s^{2}\xrightarrow {p} \sigma^{2}}$ 大数の法則によれば、

${\displaystyle \therefore {\frac {{\sqrt {n}}({\bar {X}}-\mu )}{s}}\xrightarrow {d} N(0,1)}$ 。

計算

以下に、様々なt検定を実行するために使用できる明示的な式を示します。それぞれの場合において、帰無仮説の下でt分布に正確に従うか、または近似する検定統計量の式が示されています。また、それぞれの場合において適切な自由度も示されています。これらの統計量はそれぞれ、片側検定または両側検定のいずれかを実行するために使用できます。

t値と自由度が決定したら、スチューデントのt分布の値表を用いてp値を求めることができます。算出されたp値が統計的有意性を示す閾値（通常は0.10、0.05、または0.01）を下回る場合、帰無仮説は棄却され、対立仮説が採用されます。

回帰直線の傾き

モデルを当てはめていると仮定する

${\displaystyle Y=\alpha +\beta x+\epsilon ,}$

ここで、 xは既知、αとβは未知、εは平均0、分散σ ²が未知の正規分布に従う確率変数、Yは着目する結果です。傾きβが特定の値β ₀に等しいという帰無仮説を検定します（多くの場合、β 0 は0とみなされます。この場合、帰無仮説はxとyが無相関であるというものです）。

させて

${\displaystyle {\begin{aligned}{\hat {\alpha }},{\hat {\beta }}&={\text{最小二乗推定値}},\\SE_{\hat {\alpha }},SE_{\hat {\beta }}&={\text{最小二乗推定値の標準誤差}}.\end{aligned}}}$

それから

${\displaystyle t_{\text{score}}={\frac {{\hat {\beta }}-\beta _{0}}{SE_{\hat {\beta }}}}\sim {\mathcal {T}}_{n-2}}$

帰無仮説が真であれば、自由度n − 2のt分布に従う。傾き係数の標準誤差は：

${\displaystyle SE_{\hat {\beta }}={\frac {\sqrt {\displaystyle {\frac {1}{n-2}}\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}}{\sqrt {\displaystyle \sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}}}$

残差を使って表すことができます。

${\displaystyle {\begin{aligned}{\hat {\varepsilon }}_{i}&=y_{i}-{\hat {y}}_{i}=y_{i}-({\hat {\alpha }}+{\hat {\beta }}x_{i})={\text{残差}}={\text{推定誤差}},\\{\text{SSR}}&=\sum _{i=1}^{n}{{\hat {\varepsilon }}_{i}}^{2}={\text{残差の二乗和}}.\end{aligned}}}$

t_スコアは次のように与えられる。

${\displaystyle t_{\text{score}}={\frac {({\hat {\beta }}-\beta _{0}){\sqrt {n-2}}}{\sqrt {\frac {SSR}{\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}}}.}}$

t_スコアを決定する別の方法は

${\displaystyle t_{\text{スコア}}={\frac {r{\sqrt {n-2}}}{\sqrt {1-r^{2}}}},}$

ここでrはピアソン相関係数です。

tスコア_、切片はt_{スコア、傾き}から決定できます。

${\displaystyle t_{\text{スコア,切片}}={\frac {\alpha }{\beta }}{\frac {t_{\text{スコア,傾き}}}{\sqrt {s_{\text{x}}^{2}+{\bar {x}}^{2}}}},}$

ここで、s _x ²は標本分散です。

独立2標本t検定

等しいサンプルサイズと分散

2つのグループ（1、2）がある場合、このテストは次の場合にのみ適用できます。

• 2つのサンプルサイズは同じです。
• 2つの分布は同じ分散を持つと仮定できます。

これらの仮定に違反するケースについては以下で説明します。

平均値が異なるかどうかをテストするための t統計量は次のように計算できます。

${\displaystyle t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{p}{\sqrt {\frac {2}{n}}}}},}$

どこ

${\displaystyle s_{p}={\sqrt {\frac {s_{X_{1}}^{2}+s_{X_{2}}^{2}}{2}}}.}}$

ここでs _pはn = n ₁ = n ₂のプールされた標準偏差であり、s ² _{× 1}そしてs ² _{× 2}は母分散の不偏推定値です。tの分母は2つの平均値の差の 標準誤差です。

有意性検定の場合、この検定の自由度は2 n − 2です。ここで、nはサンプルサイズです。

サンプルサイズが等しいか等しくないか、分散が似ているか（⁠1/2⁠ < ⁠s _{× 1}/s _{× 2}⁠ < 2)

この検定は、2つの分布の分散が同じであると仮定できる場合にのみ使用されます（この仮定が満たされない場合については、以下を参照してください）。前の式は、以下の式の特殊なケースであり、両方の標本サイズが等しい場合に、n = n ₁ = n ₂となります。

平均値が異なるかどうかをテストするための t統計量は次のように計算できます。

${\displaystyle t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{p}\cdot {\sqrt {{\frac {1}{n_{1}}}+{\frac {1}{n_{2}}}}}}},}$

どこ

${\displaystyle s_{p}={\sqrt {\frac {(n_{1}-1)s_{X_{1}}^{2}+(n_{2}-1)s_{X_{2}}^{2}}{n_{1}+n_{2}-2}}}}$

は2つの標本のプールされた標準偏差です。これは、母平均が同じかどうかに関わらず、その平方が共通分散の不偏推定値となるように定義されます。これらの式において、 n _i  − 1は各群の自由度の数であり、標本サイズの合計から2を引いた値（つまり、n ₁  +  n ₂  − 2）が有意差検定で使用される自由度の総数です。

最小検出効果（MDE）は以下のとおりである。^{[ 24 ]}

${\displaystyle \delta \geq {\sqrt {\frac {2S_{p}^{2}}{n}}}(t_{1-\alpha ,\nu }+t_{1-\beta ,\nu })}$

等しいまたは不等なサンプルサイズ、不等な分散（s _{X 1} > 2 s _{X 2}またはs _{X 2} > 2 s _{X 1}）

この検定はウェルチのt検定とも呼ばれ、2つの母集団分散が等しいと仮定されない場合（2つの標本サイズが等しい場合もそうでない場合も含む）にのみ用いられ、したがって別々に推定する必要がある。母集団平均が異なるかどうかを検定するための t統計量は以下のように計算される。

${\displaystyle t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{\bar {\Delta }}}},}$

どこ

${\displaystyle s_{\bar {\Delta }}={\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}.}$

ここで、s _i ^{2 は}、 2つの標本それぞれの分散の不偏推定値であり、 n _iはグループi（i = 1または2）の参加者数である。この場合、はプールされた分散ではない。有意性検定に使用するために、検定統計量の分布は、自由度が以下の式で計算される 通常のスチューデントt分布で近似される。${\displaystyle (s_{\bar {\Delta }})^{2}}$

${\displaystyle {\text{d.f.}}={\frac {\left({\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}\right)^{2}}{{\frac {(s_{1}^{2}/n_{1})^{2}}{n_{1}-1}}+{\frac {(s_{2}^{2}/n_{2})^{2}}{n_{2}-1}}}}.}$

これはウェルチ・サッタースウェイト方程式として知られています。検定統計量の真の分布は、実際には2つの未知の母分散に（わずかに）依存します（ベーレンス・フィッシャー問題を参照）。

不等分散とサンプルサイズに対する厳密な方法

この検定^{[ 25 ]}は有名なベーレンス・フィッシャー問題、すなわち、2つの独立した標本に基づいて、2つの母集団の分散が等しくないと仮定した場合に、2つの正規分布する母集団の平均の差を比較する問題を扱っています。

この検定は、 2つの母集団の標本サイズと分散が不均等な場合を考慮した正確検定として開発されました。標本サイズが極めて小さく、不均衡な場合でも（例えば、と を比較した場合）、 正確検定の性質は依然として成り立ちます。${\displaystyle \ m\equiv n_{\mathsf {X}}=50\ }$ ${\displaystyle \ n\equiv n_{\mathsf {Y}}=5\ }$

平均値が異なるかどうかをテストするための統計は次のように計算できます。

およびを、それぞれおよび からのiid サンプルベクトル (について)とします。 ${\displaystyle \ X=\left[\ X_{1},X_{2},\ldots ,X_{m}\ \right]^{\top }\ }$ ${\displaystyle \ Y=\left[\ Y_{1},Y_{2},\ldots ,Y_{n}\ \right]^{\top }\ }$ ${\displaystyle \ m\geq n\ }$ ${\displaystyle \ {\mathsf {Norm}}\left(\ \mu _{\mathsf {X}},\ \sigma _{\mathsf {X}}^{2}\ \right)\ }$ ${\displaystyle \ {\mathsf {Norm}}\left(\ \mu _{\mathsf {Y}},\ \sigma _{\mathsf {Y}}^{2}\ \right)\ }$

が 1 行目の要素がすべて である直交行列であるとし、が1 行目の要素がすべて である直交行列の最初の行であるとします。 ${\displaystyle \ (P^{\top })_{n\times n}\ }$ ${\displaystyle n\times n}$ ${\displaystyle \ {\tfrac {1}{\sqrt {n\ }}}\ ,}$ ${\displaystyle \ (Q^{\top })_{n\times m}\ }$ ${\displaystyle \ n\ }$ ${\displaystyle \ m\times m\ }$ ${\displaystyle \ {\tfrac {1}{\sqrt {m\ }}}\ }$

次に、n次元の正規乱数ベクトル は次のようになります。${\displaystyle \ Z\equiv {\frac {\ \left(Q^{\top }\right)_{n\times m}\ X\ }{\sqrt {m\ }}}\ -\ {\frac {\ \left(P^{\top }\right)_{n\times n}\ Y\ }{\sqrt {n\ }}}\ }$

${\displaystyle Z~\sim ~{\mathsf {Norm}}\left(\ \left[\ \mu _{\mathsf {X}}-\mu _{\mathsf {Y}},\ 0,\ 0,\ \ldots ,\ 0\ \right]^{\top }\ ,\ \left({\frac {\ \sigma _{\mathsf {X}}^{2}\ }{m}}+{\frac {\ \sigma _{\mathsf {Y}}^{2}\ }{n}}\right)\ I_{n}\ \right)~.}$

上記の分布から、ベクトルZの最初の要素は

${\displaystyle Z_{1}={\bar {X}}-{\bar {Y}}={\frac {1}{\ m\ }}\sum _{i=1}^{m}\ X_{i}-{\frac {1}{\ n\ }}\sum _{j=1}^{n}\ Y_{j}\ ,}$

したがって、最初の要素は次のように分布する。

${\displaystyle Z_{1}-\left(\mu _{\mathsf {X}}-\mu _{\mathsf {Y}}\right)~\sim ~{\mathsf {Norm}}\left(\ 0,\ {\frac {\ \sigma _{\mathsf {X}}^{2}\ }{m}}+{\frac {\ \sigma _{\mathsf {Y}}^{2}\ }{n}}\ \right)\ ,}$

Zの残りの要素の平方はカイ二乗分布に 従う

${\displaystyle {\frac {\ \sum _{i=2}^{n}Z_{i}^{2}\ }{\ n-1\ }}~\sim ~{\frac {\ \chi _{n-1}^{2}\ }{\ n-1\ }}\times \left({\frac {\ \sigma _{\mathsf {X}}^{2}\ }{m}}+{\frac {\ \sigma _{\mathsf {Y}}^{2}\ }{n}}\right)}$

そして直交行列PとQを構築することにより、

${\displaystyle Z_{1}-\left(\mu _{\mathsf {X}}-\mu _{\mathsf {Y}}\right)\quad \perp \quad \sum _{i=2}^{n}Z_{i}^{2}\ ,}$

したがって、 Zの最初の要素であるZ ₁は、直交性により残りの要素とは統計的に独立である。最後に、検定統計量として

${\displaystyle T_{\mathsf {e}}~\equiv ~{\frac {\ Z_{1}-\left(\mu _{\mathsf {X}}-\mu _{\mathsf {Y}}\right)\ }{\ {\sqrt {\left(\sum _{i=2}^{n}Z_{i}^{2}\right)/\left(n-1\right)\ }}\ }}~\sim ~t_{n-1}~.}$

対応のあるサンプルに対する従属t検定

この検定は、標本が従属関係にある場合、つまり、1つの標本のみが2回検定されている場合（反復測定）、または2つの標本が対応のある、あるいは「対応のある」場合に使用される。これは対応のある差の検定の例である。t統計量は次のように計算される。

${\displaystyle t={\frac {{\bar {X}}_{D}-\mu _{0}}{s_{D}/{\sqrt {n}}}},}$

ここで、 とは、すべてのペア間の差の平均と標準偏差です。ペアとは、例えば、ある人物の事前テストと事後テストのスコア、あるいは意味のあるグループ（例えば、同じ家族や年齢層から抽出されたもの：表を参照）にマッチングされた人物のペア間のスコアです。差の平均が有意に異なるかどうかを検定する場合、定数μ ₀は0です。使用される自由度はn − 1で、nはペアの数を表します。 ${\displaystyle {\bar {X}}_{D}}$ ${\displaystyle s_{D}}$

マッチしたペアの例 ペア 名前 年 テスト 1 ジョン 35 250 1 ジェーン 36 340 2 ジミー 22 460 2 ジェシー 21 200

反復測定の例 番号 名前 テスト1 テスト2 1 マイク 35% 67% 2 メラニー 50% 46% 3 メリッサ 90% 86% 4 ミッチェル 78% 91%

実例

A ₁は、6つの測定値をランダムに抽出して得られた集合を表します。

${\displaystyle A_{1}=\{30.02,\ 29.99,\ 30.11,\ 29.97,\ 30.01,\ 29.99\}}$

そして、A _{2 は}同様にして得られた2番目の集合を表すものとする。

${\displaystyle A_{2}=\{29.89,\ 29.93,\ 29.72,\ 29.98,\ 30.02,\ 29.98\}}$

たとえば、2 台の異なる機械で製造されたネジの重量などがこれに当たります。

2 つのサンプルが採取された母集団の平均は等しい という帰無仮説の検定を実行します。

2つの標本平均値の差はそれぞれX _iで表され、これは上で説明した2標本検定のアプローチすべてにおいて分子に現れる。

${\displaystyle {\bar {X}}_{1}-{\bar {X}}_{2}=0.095.}$

2つの標本の標本標準偏差はそれぞれ約0.05と0.11です。このように小さな標本数の場合、2つの母集団分散の等価性検定はあまり有効ではありません。標本サイズが等しいため、この例では2標本t検定の2つの形式は同様の結果になります。

不等分散

不等分散のアプローチ（上記）に従うと、結果は次のようになる。

${\displaystyle {\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}\approx 0.04849}$

そして自由度

${\displaystyle {\text{d.f.}}\approx 7.031.}$

検定統計量はおよそ 1.959 で、両側検定のp値は 0.09077 になります。

等分散

等分散アプローチ（上記）に従うと、結果は次のようになる。

${\displaystyle s_{p}\approx 0.08399}$

そして自由度

${\displaystyle {\text{d.f.}}=10.}$

検定統計量はおよそ 1.959 に等しく、両側p値は 0.07857 になります。

関連する統計的検定

位置問題におけるt検定の代替手段

t検定は、未知だが等しい分散を持つ2つのiid正規分布の母集団の平均が等しいかどうかの正確な検定を提供します。（ウェルチのt検定は、データが正規分布しているが分散が異なる可能性がある場合にほぼ正確な検定です。）中程度のサイズのサンプルと片側検定の場合、t検定は正規性の仮定の中程度の違反に対して比較的堅牢です。^{[ 26 ]}十分に大きなサンプルでは、​​t検定は漸近的にz検定に近づき、正規性からの大きな逸脱に対しても堅牢になります。^{[ 18 ]}

データが著しく非正規で、かつサンプルサイズが小さい場合、t検定は誤った結果をもたらす可能性があります。特定の非正規分布族に関する理論については、 ガウス尺度混合分布の位置検定を参照してください。

正規性の仮定が成り立たない場合、t検定のノンパラメトリックな代替検定の方が統計的検出力が高くなる可能性があります。しかし、データが非正規でグループ間の分散が異なる場合、t検定は一部のノンパラメトリックな代替検定よりもタイプ1の誤り制御に優れている可能性があります。 ^{[ 27 ]}さらに、後述するMann-WhitneyのU検定などのノンパラメトリックな方法では、通常、平均値の差を検定しないため、平均値の差が主な科学的関心事である場合は慎重に使用する必要があります。^{[ 18 ]}たとえば、Mann-WhitneyのU検定では、両グループが同じ分布を持つ場合、タイプ1の誤りを望ましいレベルαに維持します。また、グループBがグループAと同じ分布を持つが定数分シフトした後であるという代替検定（その場合、2つのグループの平均には確かに差がある）を検出する力もあります。しかし、グループAとグループBの分布は異なるものの、平均値は同じになるケースも考えられます（例えば、片方の分布は正の歪度を持ち、もう片方の分布は負の歪度を持ち、平均値が同じになるようにシフトされているなど）。このような場合、帰無仮説を棄却する際には、MWはαレベル以上の検出力を持つ可能性がありますが、平均値の差をそのような結果に帰することは誤りです。

外れ値がある場合、t検定は堅牢ではありません。例えば、2つの独立したサンプルについて、データ分布が非対称（つまり、分布が歪んでいる）であるか、分布の裾が大きい場合、ウィルコクソン順位和検定（マン・ホイットニーのU検定とも呼ばれる）はt検定よりも3～4倍高い検出力を持つことがあります。^{[ 26 ] [ 28 ] [ 29 ]}対応のあるサンプルのt検定のノンパラメトリック版は、対応のあるサンプルのウィルコクソン符号順位検定です。t検定とノンパラメトリック検定の選択に関する議論については、Lumleyら（2002）を参照してください。^{[ 18 ]}

一元配置分散分析(ANOVA) は、データが 2 つ以上のグループに属している場合に 2 サンプルt検定を一般化します。

対になった観察と独立した観察の両方を含むデザイン

2標本計画において、対応のある観測値と独立した観測値の両方が存在する場合、データが完全にランダムに欠損している（MCAR）と仮定すると、対応のある観測値または独立した観測値は、上記の標準検定に進むために破棄される可能性がある。あるいは、利用可能なすべてのデータを利用し、正規性とMCARを仮定すると、一般化部分重複標本t検定を使用することができる。^{[ 30 ]}

多変量テスト

スチューデントのt統計量を一般化したものは、ホテリングのt二乗統計量と呼ばれ、同じサンプル内の複数の（多くの場合相関している）尺度で仮説を検定することができます。たとえば、研究者が多数の被験者に、複数の性格尺度（ミネソタ多面性格特性目録など）からなる性格検査を受けさせるとします。このタイプの指標は通常は正の相関があるため、仮説を検定するために別々の単変量t検定を行うことは推奨されません。これは、そのような検定を行うと、指標間の共分散が無視され、少なくとも 1 つの仮説を誤って棄却する可能性が高くなるためです（タイプ I の誤り）。この場合、仮説検定には単一の多変量検定が望ましいです。検定間の正の相関についてアルファを低減して複数の検定を組み合わせるフィッシャー法がその 1 つです。もう 1 つは、ホテリングのT ²統計量がT ²分布に従うというものです。ただし、実際には、 T ²の表形式の値を見つけるのが難しいため、この分布はほとんど使用されません。通常、T ²はF統計量に変換されます。

1標本多変量検定では、平均ベクトル（μ）が与えられたベクトル（μ ₀）と等しいという仮説が立てられる。検定統計量はホテリングのt ²である。

${\displaystyle t^{2}=n({\bar {\mathbf {x} }}-{{\boldsymbol {\mu }}_{0}})'{\mathbf {S} }^{-1}({\bar {\mathbf {x} }}-{{\boldsymbol {\mu }}_{0}})}$

ここで、 nはサンプルサイズ、xは列平均のベクトル、Sはm × mのサンプル共分散行列です。

2標本多変量検定では、2標本の平均ベクトル（μ ₁、μ ₂）が等しいという仮説が立てられる。検定統計量はホテリングの2標本t ²である。

${\displaystyle t^{2}={\frac {n_{1}n_{2}}{n_{1}+n_{2}}}\left({\bar {\mathbf {x} }}_{1}-{\bar {\mathbf {x} }}_{2}\right)'{\mathbf {S} _{\text{pooled}}}^{-1}\left({\bar {\mathbf {x} }}_{1}-{\bar {\mathbf {x} }}_{2}\right).}$

2標本t検定は単回帰の特殊なケースである。

2標本t検定は単純線形回帰の特殊なケースである^{[ 31 ] [ 32 ] [ 33 ] [ 34 ] [ 35 ]} 。^{[ 36 ]}この関係は次の例で説明される。

臨床試験では、6人の患者に薬剤またはプラセボを投与します。3人の患者には薬剤を0単位（プラセボ群）投与し、3人の患者には薬剤を1単位（実薬群）投与します。治療終了時に、研究者は各患者が記憶テストで思い出せる単語数について、ベースラインからの変化を測定します。

患者の単語想起と薬剤投与量の値の表を以下に示します。

忍耐強い	薬の投与量	単語を思い出す
1	0	1
2	0	2
3	0	3
4	1	5
5	1	6
6	1	7

Rプログラミング言語とt検定および線形回帰の関数を用いた分析用のデータとコードが提供されています。以下は、Rで生成された上記と同じ（架空の）データ t.testです。lm

> word.recall.data = data.frame ( drug.dose = c ( 0 , 0 , 0 , 1 , 1 , 1 ), word.recall = c ( 1 , 2 , 3 , 5 , 6 , 7 ))

t検定を実行します。var.equal=Tこの分析を単回帰分析と完全に同等にするには、 等分散の仮定が必要であることに注意してください。

> ( word.recall.data 、t.test ( word.recall ~ drug.dose 、var.equal = T ))で

R コードを実行すると、次の結果が得られます。

• 薬物投与量 0 のグループの平均単語想起は 2 です。
• 1 種類の薬剤を投与したグループの平均単語想起は 6 です。
• 治療グループ間の平均単語想起の差は 6 – 2 = 4 です。
• 薬物投与量間の単語想起の差は有意であった（p=0.00805）。

同じデータに対して線形回帰を実行します。lm()線形モデル用のR関数を使用して計算を実行できます。

> word.recall.data.lm = lm ( word.recall ~ drug.dose 、data = word.recall.data ) > summary ( word.recall.data.lm )

線形回帰では、係数と p 値の表が提供されます。

係数	見積もり	標準誤差	t値	p値
インターセプト	2	0.5774	3.464	0.02572
薬の投与量	4	0.8165	4.899	0.000805

係数表から次の結果が得られます。

• 切片の推定値 2 は、薬物投与量が 0 の場合の単語想起の平均値です。
• 薬剤投与量の推定値4は、薬剤投与量が1単位（0から1へ）変化すると、平均単語想起が4単位（2から6へ）変化することを示しています。これは、2つの群の平均を結んだ直線の傾きです。
• 4の傾きが0と異なるp値はp = 0.00805です。

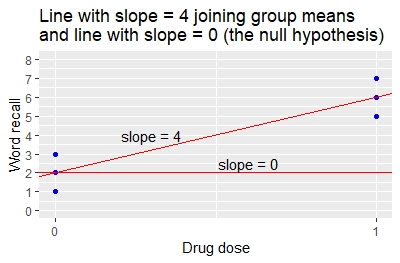
線形回帰の係数は、グラフに示されているように、2つのグループの平均を結ぶ直線の傾きと切片を指定します。切片は2、傾きは4です。

線形回帰の結果をt検定の結果と比較します。

• t検定から、グループ平均間の差は6-2=4です。
• 回帰分析から、傾きも 4 であり、薬物投与量の 1 単位の変化 (0 から 1) により、平均単語想起が 4 単位変化する (2 から 6) ことを示しています。
• 平均値の差に関するt検定のp値と傾きに関する回帰p値はどちらも0.00805です。どちらの方法でも同じ結果が得られます。

この例では、0と1の値を持つ単一のx変数を持つ単回帰の特殊なケースにおいて、t検定は線形回帰と同じ結果を与えることを示しています。この関係は代数的にも表すことができます。

t検定と線型回帰の関係性を認識することで、多重線型回帰や多元配置分散分析の利用が容易になります。これらのt検定の代替手法では、応答に関連する追加の説明変数を含めることができます 。回帰分析や分散分析を用いてこのような追加の説明変数を含めることで、本来説明できない分散が減少し、2標本t検定よりも差異を検出する力が高まる傾向があります。^{[ 37 ]}

t検定の検出力とサンプルサイズ

検定の検出力は、対立仮説が正しい場合に検定で帰無仮説を棄却する確率です。

2標本t検定の検出力計算には以下の情報が必要である。^{[ 38 ]}

• 2つのグループの平均の差
• グループ内標準偏差（2つのグループの標準偏差が同じ場合）
• 各グループのサンプルサイズ（被験者数）
• 有意性に必要なp値（アルファ）

検出力を計算するには、標準化効果量を計算すると便利です。これは、2つの平均値の差をグループ内標準偏差で割った値です。例えば、グループAの平均が14、グループBの平均が10で、グループ内標準偏差が8単位（2つのグループの標準偏差が同じであると仮定）であるとします。この場合、グループ平均値の差は14-10 = 4単位となり、標準化効果量は(14-10)/8 = 4/8 = 0.5となります。

下のグラフは、グループあたりの被験者数が同数であると仮定し、標準化効果サイズが0.1から1、グループあたりのサンプルサイズが10から50の場合の検出力を示しています。グループあたりのNは、各グループの観測値の数です。例えば、標準化効果サイズが0.5の場合、グループあたりのサンプルサイズがN = 10の場合は検出力は0.2をわずかに下回りますが、グループあたりのサンプルサイズがN = 50の場合は検出力は約0.7になります。

2標本t検定の検出力と標準化効果量および標本数との関係を示すグラフ

検出力とサンプル サイズの計算ツールは、次のような多くの Web サイトで入手できます。

サンプルサイズ計算機

2つの独立した平均を比較するためのサンプルサイズ計算機

検出力とサンプル サイズに関する無料のソフトウェア パッケージについては、これらの Web サイトで説明されています。

2群独立標本t検定の検出力分析 | Rデータ分析例

G*パワー

追伸

次のような商用ソフトウェア パッケージは、t 検定やその他の多くの統計検定の検出力とサンプル サイズを提供します。

サンプルサイズソフトウェア | 検出力分析ソフトウェア | PASS | NCSS.com

nQuery で臨床試験の設計を最適化

[1]

IBM SPSS統計

Stataにおける検出力とサンプルサイズの特徴

Minitab にはどのような検出力とサンプル サイズの分析が含まれていますか?

ソフトウェア実装

QtiPlot、LibreOffice Calc、Microsoft Excel、SAS、SPSS、Stata、DAP、gretl、R、Python、PSPP、Wolfram Mathematica、MATLAB、Minitabなどの多くのスプレッドシートプログラムや統計パッケージには、Student t検定の実装が含まれています。

言語/プログラム	関数	注記
Microsoft Excel 2010 以前	TTEST(array1, array2, tails, type)	[2]
Microsoft Excel 2010以降	T.TEST(array1, array2, tails, type)	[3]
アップルの数字	TTEST(sample-1-values, sample-2-values, tails, test-type)	[4]
LibreOffice Calc	TTEST(Data1; Data2; Mode; Type)	[5]
Googleスプレッドシート	TTEST(range1, range2, tails, type)	[6]
パイソン	scipy.stats.ttest_ind(a, b, equal_var=True)	[7]
MATLAB	ttest(data1, data2)	[8]
マセマティカ	TTest[{data1,data2}]	[9]
R	t.test(data1, data2, var.equal=TRUE)	[10]
SAS	PROC TTEST	[11]
ジャワ	tTest(sample1, sample2)	[12]
ジュリア	EqualVarianceTTest(sample1, sample2)	[13]
スタタ	ttest data1 == data2	[14]

参照

• 条件付き変更モデル
• 同等性検定 – 観測データから統計的推論を導き出すために使用されるツール
• F検定 – 主に複数の制約を用いた統計的仮説検定
• 検出力分析における非心t分布 – 確率分布
• スチューデントのt統計量 – 統計における比率Pages displaying short descriptions of redirect targets
• Z検定 – 統計的検定
• マン・ホイットニーU検定 – 帰無仮説のノンパラメトリック検定
• t検定におけるシダック補正 – 統計的手法
• ウェルチのt検定 – 2つの母集団の平均値が等しいかどうかを統計的に検定する
• 分散分析 - 統計モデルの収集（ANOVA）
• t分布 – 確率分布
• 正規分布の平均の信頼区間（こちらも）

参考文献

1. 健康と病気におけるマイクロバイオーム. アカデミックプレス. 2020年5月29日. p. 397. ISBN 978-0-12-820001-8。
2. ザボ、イシュトヴァーン (2003)。 「Systeme aus einer endlichen Anzahl starrer Körper」。Einführung in die Technische Mechanik (ドイツ語)。シュプリンガー ベルリン ハイデルベルク。 pp.  196–199。doi : 10.1007/978-3-642-61925-0_16 (2025 年 7 月 12日に非アクティブ)。ISBN 978-3-540-13293-6。
3. シュリヴィッチ、B. (1937 年 10 月)。 「Untersuhungen über den anasomotischen Kanal zwischen der Arteria coeliaca und mesenterica優れた und damit in Zusammenhang stehende Fragen」。Zeitschrift für Anatomy und Entwicklungsgeschichte (ドイツ語)。107 (6): 709–737 .土井: 10.1007/bf02118337。ISSN 0340-2061。S2CID 27311567。  
4. ヘルマート (1876)。「Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Beobachtungsfehlers 監督 Beobachtungen gleicher Genauigkeit」。Astronomische Nachrichten (ドイツ語)。88 ( 8–9 ): 113–131 . Bibcode : 1876AN....88....113H。土井：10.1002/asna.18760880802。
5. ルーロス、J. (1876)。「Vergleichung von zwei Werthen des wahrscheinlichen Fehlers」。Astronomische Nachrichten (ドイツ語)。87 (14): 209–220。ビブコード: 1876AN....87....209L。土井：10.1002/asna.18760871402。
6. Pfanzagl, J. (1996). 「確率統計史研究 XLIV. t分布の先駆者」. Biometrika . 83 (4): 891– 898. doi : 10.1093/biomet/83.4.891 . MR 1766040 . 
7. シェイニン、オスカー (1995). 「ヘルメルトの誤差理論における研究」.正確科学史アーカイブ. 49 (1): 73– 104. doi : 10.1007/BF00374700 . ISSN 0003-9519 . S2CID 121241599 .  
8. ピアソン、カール (1895). 「X. 進化の数学的理論への貢献.—II. 均質物質における歪変化」 .ロンドン王立協会哲学論文集 A. 186 : 343–414 . Bibcode : 1895RSPTA.186..343P . doi : 10.1098 /rsta.1895.0010 .
9. Student (1908). 「平均値の確率誤差」(PDF) . Biometrika . 6 (1): 1– 25. doi : 10.1093/biomet/6.1.1 . hdl : 10338.dmlcz/143545 . 2016年7月24日閲覧.
10. Wendl, Michael C. (2016). 「偽名の名声」. Science . 351 (6280): 1406. doi : 10.1126/science.351.6280.1406 . PMID 27013722 . 
11. ウォルポール, ロナルド・E. (2006).エンジニアと科学者のための確率と統計. マイヤーズ, H. レイモンド (第7版). ニューデリー: ピアソン. ISBN 81-7758-404-9. OCLC  818811849 .
12. Raju, TN (2005). 「ウィリアム・シーリー・ゴセットとウィリアム・A・シルバーマン：二人の科学の『学生』」.小児科学. 116 (3): 732– 735. doi : 10.1542/peds.2005-1134 . PMID 16140715. S2CID 32745754 .  
13. ドッジ、ヤドラー(2008). 『統計の簡潔な百科事典』 シュプリンガー・サイエンス＆ビジネス・メディア. pp.  234– 235. ISBN 978-0-387-31742-7。
14. ファデム、バーバラ（2008年）『ハイ・イールド行動科学』ハイ・イールド・シリーズ、メリーランド州ヘイガーズタウン：リッピンコット・ウィリアムズ＆ウィルキンス、ISBN 9781451130300。
15. ライス、ジョン・A. (2006).数理統計とデータ分析（第3版）. ダックスベリー・アドバンスト.
16. Weisstein, Eric. 「スチューデントのt分布」 . mathworld.wolfram.com .
17. David, H. A.; Gunnink, Jason L. (1997). 「人工ペアリング下における対応のあるt検定」. The American Statistician . 51 (1): 9– 12. doi : 10.2307/2684684 . JSTOR 2684684 . 
18. Lumley, Thomas; Diehr, Paula ; Emerson, Scott; Chen, Lu (2002年5月). 「大規模公衆衛生データセットにおける正規性仮定の重要性」 . Annual Review of Public Health . 23 (1): 151– 169. doi : 10.1146/annurev.publhealth.23.100901.140546 . ISSN 0163-7525 . PMID 11910059 .  
19. Markowski, Carol A.; Markowski, Edward P. (1990). 「予備的分散検定の有効性のための条件」. The American Statistician . 44 (4): 322– 326. doi : 10.2307/2684360 . JSTOR 2684360 . 
20. Guo, Beibei; Yuan, Ying (2017). 「部分的に対応のあるデータを用いた平均値比較手法の比較レビュー」.統計的医学研究手法. 26 (3): 1323– 1340. doi : 10.1177/0962280215577111 . PMID 25834090. S2CID 46598415 .  
21. ブランド、マーティン（1995年）『医療統計入門』オックスフォード大学出版局、168ページ。ISBN 978-0-19-262428-4。
22. 「中心極限定理と正規性仮定 > 正規性 > 連続分布 > 分布 > 統計リファレンスガイド | Analyse-it® 6.15ドキュメント」 . analyse-it.com . 2024年5月17日閲覧。
23. DEMİR, Süleyman (2022-06-26). 「歪度と尖度係数の異なるサンプルサイズにおける正規性検定の比較」 .国際教育評価ツールジャーナル. 9 (2): 397– 409. doi : 10.21449/ijate.1101295 . ISSN 2148-7456 . 
24. 「私の Webspace ファイル」(PDF) . webspace.ship.edu .
25. Wang, Chang; Jia, Jinzhu (2022). 「Te検定：ベーレンス・フィッシャー問題のための新しい非漸近的T検定」. arXiv : 2210.16473 [ math.ST ].
26. Sawilowsky, Shlomo S.; Blair, R. Clifford (1992). 「母集団正規性からの逸脱に対するt検定の堅牢性とタイプII誤差特性のより現実的な考察」Psychological Bulletin . 111 (2): 352– 360. doi : 10.1037/0033-2909.111.2.352 .
27. ジマーマン、ドナルド W. (1998年1月). 「二つの仮定の同時違反によるパラメトリックおよびノンパラメトリック統計検定の無効化」.実験教育ジャーナル. 67 (1): 55– 68. doi : 10.1080/00220979809598344 . ISSN 0022-0973 . 
28. Blair, R. Clifford; Higgins, James J. (1980). 「様々な非正規分布下におけるWilcoxonの順位和統計量とStudentのt統計量の検出力の比較」. Journal of Educational Statistics . 5 (4): 309– 335. doi : 10.2307/1164905 . JSTOR 1164905 . 
29. Fay, Michael P.; Proschan, Michael A. (2010). 「Wilcoxon–Mann–Whitney検定かt検定か？仮説検定における仮定と意思決定ルールの多重解釈について」 .統計調査. 4 : 1– 39. doi : 10.1214/09-SS051 . PMC 2857732. PMID 20414472 .  
30. Derrick, B; Toher, D; White, P (2017). 「対応のある観測値と独立した観測値を含む2つの標本の平均値を比較する方法：Derrick, Russ, Toher and White (2017) の補足資料」(PDF) .心理学のための定量的手法. 13 (2): 120– 126. doi : 10.20982/tqmp.13.2.p120 .
31. Kutner, Michael H.; Nachtsheim, CJ.; Neter, John (2004),応用線形回帰モデル, McGraw-Hill, ISBN 9780073521442
32. ウォーカー、マイケル（2024）、生物学研究でp値を0.05未満にする方法：検出力を高め、サンプルサイズを減らし、より良い統計テストを選択する方法の実践例（PDF）、Amazon、ISBN 979-8877882577
33. Pandis, Nikolaos J (2016). 「t検定と分散分析における線形回帰の使用」 . American Journal of Orthodontics and Dentofacial Orthopedics . 149 (5p769May): 269– 284.
34. 線形回帰の特殊なケースとしての2標本t検定
35. Rにおける線形モデルとしての独立t検定
36. 2.9 2標本t検定と線形回帰の関係の構築
37. Shieh, Gwowen (2020年3月). 「ANCOVAデザインにおける検出力分析とサンプルサイズ計画」 . Psychometrika . 85 ( 1): 101– 120. doi : 10.1007/s11336-019-09692-3 . ISSN 1860-0980 . PMC 8225521. PMID 31823115 .   
38. Julious, Steven A. (2010)、「臨床試験のサンプルサイズ」、Chapman and Hall/CRC、ISBN 978-1584887393

出典

• オマホニー、マイケル（1986年）『食品の官能評価：統計的手法と手順』CRC Press、p.487、ISBN 0-82477337-3。
• ウィリアム・H・プレス、ソール・A・テウコルスキー、ウィリアム・T・ベタリング、ブライアン・P・フラナリー (1992). 『C言語による数値計算法：科学計算の芸術』ケンブリッジ大学出版局. 616ページ . ISBN 0-521-43108-5。

さらに読む

• Boneau, C. Alan (1960). 「 t検定の根底にある仮定の違反の影響」.心理学速報. 57 (1): 49– 64. doi : 10.1037/h0041412 . PMID  13802482 .
• Edgell, Stephen E.; Noon, Sheila M. (1984). 「正規性違反が相関係数のt検定に及ぼす影響」心理学速報. 95 (3): 576– 583. doi : 10.1037/0033-2909.95.3.576 .
• Chicco D.; Sichenze A.; Jurman G. (2025). 「生物統計学におけるスチューデントt検定、マン・ホイットニーU検定、カイ2乗検定、クラスカル・ワリス検定の利用に関する簡単なガイド」 . BioData Mining . 18 (56) 56: 1– 51. doi : 10.1186/s13040-025-00465-6 . PMC  12366075. PMID  40835959 .

外部リンク

• 「学生テスト」数学百科事典EMSプレス2001[1994]。
• Trochim, William MK「T検定」、研究方法知識ベース、conjoint.ly
• マーク・トーマによるYouTubeでの計量経済学講義（トピック：仮説検定）