16セル
16細胞（4-オルソプレックス）
シュレーゲル図（頂点と辺）
タイプ凸正多面体、4次元正多面体、4次元半立方体、4次元半立方体
シュレーフリ記号{3,3,4}
コクセター図
細胞16 {3,3}
顔32 {3}
エッジ24
頂点8
頂点図形八面体
ペトリー多角形八角形
コクセターグループB 4 , [3,3,4], 順序 384 D 4 , 順序 192
デュアルテッセラクト
プロパティ凸面、等角面、等等面体、等面体、正則、ハンナー多面体
均一インデックス12

幾何学において、16胞体（じゅうしゅたい）は、シュレーフリ記号{3,3,4}で表される正凸4次元多面体（プラトン立体の4次元版）である。これは、19世紀半ばにスイスの数学者ルートヴィヒ・シュレーフリによって初めて記述された6つの正凸4次元多面体のうちの1つである。 [ 1 ] C16、ヘキサデカコローン[ 2 ]、ヘキサデカヘドロイド[ sic ? ]とも呼ばれる。[ 3 ]

これは、交差多面体、正多面体、あるいは超八面体と呼ばれる無限の多面体族の4次元の要素であり、三次元の八面体と類似している。これはコクセターの多面体である。[ 4 ]双対多面体は四次元立方体（4-立方体）であり、これと組み合わせることで複合図形を形成することができる。16セルのセルは、四次元立方体の16頂点と双対である。 β4{\displaystyle \beta _{4}}

幾何学

16セルは、6つの凸正4次元多面体のシーケンスの中で2番目です（サイズと複雑さの順）。[ a ]

4つの後継凸正4多面体はそれぞれ、複数の16セルの多面体複合体の凸包として構築できます。16頂点のテッセラクト（四次元体）は2つの16セルの複合体として、24頂点の24セルは3つの16セルの複合体として、120頂点の600セルは15個の16セルの複合体として、600頂点の120セルは75個の16セルの複合体として構築されます。[ b ]

正凸4次元多面体
対称群A4​B4​F4​H4​
名前 5セル

超四面体 5点

16セル

超八面体 8点

8セル

ハイパーキューブ 16ポイント

24セル

24ポイント

600セル

超二十面体 120点

120セル

超十二面体 600ポイント

シュレーフリ記号{3, 3, 3} {3, 3, 4} {4, 3, 3} {3, 4, 3} {3, 3, 5} {5, 3, 3}
コクセターミラー
鏡面二面角 ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/5⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠⁠𝝅/5⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠
グラフ
頂点 5つの四面体 8面体 16 四面体 24立方体 120面体 600四面体
エッジ10個の三角形 24平方 32 三角形 96三角形 720五角形 1200 三角形
顔 10個の三角形 32個の三角形 24個の正方形 96個の三角形 1200個の三角形 720個の五角形
細胞 5つの四面体 16個の四面体 8個のキューブ 24個の八面体 600個の四面体 120面体
トリ1 5面体2 8面体2 4キューブ4 6面体20 30四面体12 10面体
内接 120セルで120個 120セルで675 2 16セル 3 8セル 25 24セル 10 600セル
素晴らしいポリゴン2つの正方形×3 長方形4つ×4 4つの六角形×4 12角形×6 不規則な六角形100 個x 4
ペトリー多角形五角形1個×2 八角形1個×3 八角形2個×4 十二角形2個×4 30角形4個×6 20 30角形x 4
長半径 1{\displaystyle 1}1{\displaystyle 1}1{\displaystyle 1}1{\displaystyle 1}1{\displaystyle 1}1{\displaystyle 1}
エッジの長さ 52≈1.581{\displaystyle {\sqrt {\tfrac {5}{2}}}\approx 1.581}2≈1.414{\displaystyle {\sqrt {2}}\approx 1.414}1{\displaystyle 1}1{\displaystyle 1}1ϕ≈0.618{\displaystyle {\tfrac {1}{\phi }}\approx 0.618}1ϕ22≈0.270{\displaystyle {\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\approx 0.270}
短い半径 14{\displaystyle {\tfrac {1}{4}}}12{\displaystyle {\tfrac {1}{2}}}12{\displaystyle {\tfrac {1}{2}}}12≈0.707{\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}ϕ48≈0.926{\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926}ϕ48≈0.926{\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926}
エリア 10(538)≈10.825{\displaystyle 10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\approx 10.825}32(34)≈27.713{\displaystyle 32\left({\sqrt {\tfrac {3}{4}}}\right)\approx 27.713}24{\displaystyle 24}96(316)≈41.569{\displaystyle 96\left({\sqrt {\tfrac {3}{16}}}\right)\approx 41.569}1200(34ϕ2)≈198.48{\displaystyle 1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\approx 198.48}720(25+1058ϕ4)≈90.366{\displaystyle 720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\approx 90.366}
音量 5(5524)≈2.329{\displaystyle 5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\approx 2.329}16(13)≈5.333{\displaystyle 16\left({\tfrac {1}{3}}\right)\approx 5.333}8{\displaystyle 8}24(23)≈11.314{\displaystyle 24\left({\tfrac {\sqrt {2}}{3}}\right)\approx 11.314}600(212ϕ3)≈16.693{\displaystyle 600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\approx 16.693}120(15+754ϕ68)≈18.118{\displaystyle 120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\approx 18.118}
4-コンテンツ 524(52)4≈0.146{\displaystyle {\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146}23≈0.667{\displaystyle {\tfrac {2}{3}}\approx 0.667}1{\displaystyle 1}2{\displaystyle 2}Short×Vol4≈3.863{\displaystyle {\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863}Short×Vol4≈4.193{\displaystyle {\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193}

座標

分離した正方形
xy平面
（0, 1, 0, 0）( 0, 0,-1, 0 )
（0、0、1、0）( 0,-1, 0, 0)
wz飛行機
（1、0、0、0）（0, 0, 0,-1）
（0、0、0、1）(-1, 0, 0, 0)

16 セルは 4 次元交差多面体 (4 直交多面体)であり、その頂点は (w、x、y、z) 直交座標系の 4 つの軸上で反対のペアになっていることを意味します。

8つの頂点は(±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1)です。すべての頂点は、対角の頂点を除いて辺で結ばれています。辺の長さは√2です。

頂点座標は、6つの座標平面上に位置する6つの直交中心正方形を形成する。軸を共有しない対向平面（例えばxy平面とwz平面）上の正方形は完全に互いに交わらない（どの頂点でも交差しない）。これらの平面は完全に直交する。[ c ]

16 セルは、その頂点が 4 つの直交軸を正確に定義するため、4 次元参照フレームの選択に対する 直交基底を構成します。

構造

16セルのシュレーフリ記号は{3,3,4}で、セルが正四面体{3,3}、頂点図形が正八面体{3,4}であることを示しています。四面体は8つ、三角形は12個、そしてすべての頂点には6つの辺が接しています。辺図形は正方形です。四面体は4つ、三角形は4つ、すべての辺には4つの辺が接しています。

16 セルは16 個のセルによって囲まれており、そのすべてが正四面体です。[ e ] 16 セルには 32 の三角形の面、24の辺、8 つの頂点があります。24 の辺は、 6 つの座標平面 (3 組の完全に直交する大正方形) にある大円上にある 6 つの直交中心正方形を囲んでいます。各頂点では、3 つの大正方形が垂直に交差しています。6 つの辺は、標準的な八面体ピラミッドの頂点で 6 つの辺が交わるのと同じように、頂点で交わります。[ d ] 16 セルの 6 つの直交中心平面は、それぞれが3 つの直交大正方形を持つ八面体を形成する 4 つの直交中心超平面 (3 次元空間) に分割できます。

回転

単純な回転を行う16セルの3D投影二重回転を行う16セルの3D投影

4 次元ユークリッド空間での回転は、完全に直交する平面での 2 つの 2 次元回転の合成として考えることができます。 [ 6 ] 16 セルは、4 次元回転を観察するための単純なフレームです。16 セルの 6 つの大きな正方形のそれぞれに、もう 1 つの完全に直交する大きな正方形があるためです (完全に直交する正方形のペアが 3 つあります)。[ c ] 16 セルの多くの回転は、その大きな正方形平面の 1 つ (たとえばxy平面) の回転角度と、完全に直交する大きな正方形平面 ( wz平面) の別の回転角度によって特徴付けることができます。[ i ]完全に直交する大きな正方形には、互いに素な頂点があります。つまり、16 セルの 8 つの頂点のうち 4 つは 1 つの平面で回転し、残りの 4 つは完全に直交する平面で独立して回転します。[ f ]

2次元または3次元では、回転は単一の回転面によって特徴付けられます。4次元空間で行われるこの種の回転は単純回転と呼ばれ、2つの完全に直交する面のうち1つだけが回転します（もう一方の面の回転角度は0です）。16セルでは、6つの直交面のうち1つにおける単純回転では、8つの頂点のうち4つだけが移動し、残りの4つは固定されたままです。（上記の単純回転アニメーションでは、回転面が6つの直交基底面のいずれにも該当しないため、8つの頂点すべてが移動します。）

二重回転では、4つの頂点の組は両方とも独立して動きます。回転角度は、2つの完全に直交する平面で異なる場合があります。2つの角度が同じ場合は、最大対称性を持つ等傾斜回転が発生します。[ p ] 16セルにおいて、任意の完全に直交する正方形平面のペアを90度等傾斜回転させる場合、すべての正方形平面は、その完全に直交する正方形平面に戻ります。[ q ]

建設

八面体二錐体

八面体β3{\displaystyle \beta _{3}}16セルβ4{\displaystyle \beta _{4}}
六角形超平面を歪める直交投影

16セルの最も単純な構成は、3次元交差多面体である正八面体上に構築されます。正八面体は3本の垂直軸と、3対の対角に6つの頂点を持ちます（ペトリー多角形は六角形です）。他の3つの軸すべてに垂直な4つ目の軸上に、もう1組の頂点を追加します。新しい頂点をそれぞれ元の6つの頂点すべてに接続し、12の新しい辺を追加します。これにより、16セルの中心超平面に位置する共有正八面体底辺上に2つの正八面体ピラミッドが形成されます。 [ 10 ]

16セルの6つの直交中心正方形を大円に立体投影したもの。各円は、3つの円が直交する交点で4つの円弧に分割されます。各円には、交差しないクリフォード平行円が1つあることに注目してください。これらの2つの円は、鎖の隣接するリンクのように互いに通過します。

構築の出発点となる八面体には、3つの直交する正方形（六角形投影では長方形として表示されます）があります。各正方形は、他の正方形とそれぞれ2つの対角頂点で交差し、各頂点で2つの正方形が交差します。次に、4次元（3次元超平面の上下）にさらに2つの点が追加されます。これらの新しい頂点は八面体のすべての頂点に接続され、12の新たな辺と3つの正方形（投影では六角形の3つの直径として側面から表示されます）、そしてさらに3つの八面体が作成されます。[ g ]

前例のないものも作られました。各正方形はもはや他のすべての正方形と交差していないことに注目してください。4 つの正方形と交差しています (各頂点で3 つの正方形が交差しています)。ただし、各正方形には、頂点を共有していない他の正方形が1 つあります。つまり、その正方形とは直接接続されていません。これら 2 つの別々の垂直な正方形 (3 組あります) は、四面体の反対側の辺のようなものです。垂直ですが、交差していません。これらは、互いに向かい合って位置し (ある意味では平行)、接触していませんが、鎖の 2 つの垂直なリンクのように、互いを貫通しています (ただし、鎖のリンクとは異なり、共通の中心があります)。これらはクリフォード平行面の例であり、16 セルはこれらが発生する最も単純な正多面体です。1次元以上の物体（単なる曲線ではない）のクリフォード平行性[ k ]はここで現れ、その後の4次元正多面体すべてに現れる。これは、互いに素な同心正4次元多面体とその対応する部分との間の定義関係と見ることができる。これは、2次元以上の合同な（相似な）多面体間でも起こり得る。[ 11 ]例えば、上で述べたように、その後の凸正4次元多面体はすべて複数の16次元セルの複合体であり、それらの16次元セルはクリフォード平行多面体である。

四面体構造

16セルには、正四面体を用いたウィトフ構成が2つあります。正四面体と交互構成です。交互構成はここでは網目として示されており、後者は2色が交互に現れる四面体セルで表されています。交互構成は、16セルの対称性が低い構成で、デミテッセラクトと呼ばれます。

ワイトホフの構築は、16 セルの特性 5 セルを万華鏡のような鏡で複製する。すべての正 4 多面体には、特性 4 直交配位、つまり不規則な 5 セルがある。[ r ]正 4 多面体には、 5 セル、16 セル、600 セルの 3 つがある。いずれも正四面体セルで囲まれているが、その特性 5 セル (4 直交配位) はそれぞれ異なる四面体ピラミッドであり、すべて同じ特性不規則四面体に基づいている。これらは同じ種類のセルを持つため、同じ特性四面体(3 直交配位) と特性直角三角形(2 直交配位) を共有している。[ s ]

16セルの特徴[ 13 ]
エッジ[ 14 ]アーク 二面角[ 15 ]
𝒍 2≈1.414{\displaystyle {\sqrt {2}}\approx 1.414}90°π2{\displaystyle {\tfrac {\pi }{2}}}120°2π3{\displaystyle {\tfrac {2\pi }{3}}}
𝟀 23≈0.816{\displaystyle {\sqrt {\tfrac {2}{3}}}\approx 0.816}60インチπ3{\displaystyle {\tfrac {\pi }{3}}}60°π3{\displaystyle {\tfrac {\pi }{3}}}
𝝉 [ t ]12≈0.707{\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}45インチπ4{\displaystyle {\tfrac {\pi }{4}}}45°π4{\displaystyle {\tfrac {\pi }{4}}}
𝟁 16≈0.408{\displaystyle {\sqrt {\tfrac {1}{6}}}\approx 0.408}30インチπ6{\displaystyle {\tfrac {\pi }{6}}}60°π3{\displaystyle {\tfrac {\pi }{3}}}
0R3/l{\displaystyle _{0}R^{3}/l}34≈0.866{\displaystyle {\sqrt {\tfrac {3}{4}}}\approx 0.866}60°π3{\displaystyle {\tfrac {\pi }{3}}}90°π2{\displaystyle {\tfrac {\pi }{2}}}
1R3/l{\displaystyle _{1}R^{3}/l}14=0.5{\displaystyle {\sqrt {\tfrac {1}{4}}}=0.5}45°π4{\displaystyle {\tfrac {\pi }{4}}}90°π2{\displaystyle {\tfrac {\pi }{2}}}
2R3/l{\displaystyle _{2}R^{3}/l}112≈0.289{\displaystyle {\sqrt {\tfrac {1}{12}}}\approx 0.289}30°π6{\displaystyle {\tfrac {\pi }{6}}}90°π2{\displaystyle {\tfrac {\pi }{2}}}
0R4/l{\displaystyle _{0}R^{4}/l}1{\displaystyle 1}
1R4/l{\displaystyle _{1}R^{4}/l}12≈0.707{\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}
2R4/l{\displaystyle _{2}R^{4}/l}13≈0.577{\displaystyle {\sqrt {\tfrac {1}{3}}}\approx 0.577}
3R4/l{\displaystyle _{3}R^{4}/l}14=0.5{\displaystyle {\sqrt {\tfrac {1}{4}}}=0.5}

通常の16セルの特性5セルは、コクセター・ディンキン図で表される。は、鏡面間の二面角のリストとして読み取ることができます。これは、正四面体の特性四面体に基づく不規則四面体ピラミッドです。正16セルは、対称超平面によって、その中心で交わる特性5セルのインスタンス384個に分割されます。

特性 5 セル (4-正方格子) には、その基本特性四面体 (3-正方格子) よりも 4 つの辺が多く、底辺の 4 つの頂点を頂点 (4-正方格子の 5 番目の頂点、正 16 セルの中心) に接続します。[ u ]正 16 セルが単位半径の辺と辺の長さ 𝒍 = である場合、その特性 5 セルの 10 辺の長さは、その外部直角三角形面の周りで 、 、 (特性角 𝟀、𝝉、𝟁 の反対側の辺) 、[ t ]、、 (特性四面体の外部 3-正方格子面の他の 3 辺で、正四面体の特性半径)、および、、、(正 16 セルの特性半径の辺) となります。オルソスキームの直交エッジに沿った 4 エッジ パスは、、、、で、最初に 16 セルの頂点から 16 セルのエッジ中心まで進み、次に 90° 回転して 16 セルの面中心まで進み、次に 90° 回転して 16 セルの四面体セル中心まで進み、最後に 90° 回転して 16 セル中心まで進みます。 2{\displaystyle {\sqrt {2}}}23{\displaystyle {\sqrt {\tfrac {2}{3}}}}12{\displaystyle {\sqrt {\tfrac {1}{2}}}}16{\displaystyle {\sqrt {\tfrac {1}{6}}}}34{\displaystyle {\sqrt {\tfrac {3}{4}}}}14{\displaystyle {\sqrt {\tfrac {1}{4}}}}112{\displaystyle {\sqrt {\tfrac {1}{12}}}}1{\displaystyle 1}12{\displaystyle {\sqrt {\tfrac {1}{2}}}}13{\displaystyle {\sqrt {\tfrac {1}{3}}}}14{\displaystyle {\sqrt {\tfrac {1}{4}}}}12{\displaystyle {\sqrt {\tfrac {1}{2}}}}16{\displaystyle {\sqrt {\tfrac {1}{6}}}}14{\displaystyle {\sqrt {\tfrac {1}{4}}}}14{\displaystyle {\sqrt {\tfrac {1}{4}}}}

らせん構造

ボアダイク・コクセター螺旋に見られる、8つの面結合四面体からなる4次元リング。3つの異なる色の8辺を持つ円形のパスで囲まれており、3次元空間に切り取られて平らに配置されている。等傾斜軸（図示なし）と、4次元全体をねじりながら8つの頂点すべてを通過する円周4𝝅の螺旋円が含まれている。[ n ]切り取られたリングの両端にある2つの青青黄の三角形は同じ物体である。
ネットと直交投影

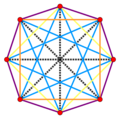
16 セルは、 8 つの連鎖四面体からなるBoerdijk–Coxeter らせん2 つから構築できます。各四面体は 4 次元でリング状に曲げられています。[ 16 ] [ 17 ] 2 つの円形らせんは互いの周りを螺旋状に回り、互いに入れ子になり、互いを貫通してホップリンクを形成します。16 個の三角形面は三角形のタイリング内の 2D ネットで表示でき、各頂点の周りに 6 つの三角形があります。紫色のエッジは16 セルのペトリー多角形を表しています。8 セルの四面体リングには、異なる色の 3 つの八芒星、つまり八芒星の 3 番目の頂点ごとに 16 セルの周りを 2 回巻く 8 辺の円形パスが含まれています。オレンジと黄色のエッジは、1 つの八芒星の 4 辺の半分 2 つで、その両端を結合してメビウスの帯を形成します。

このように、16セルは、それぞれ8つの四面体からなる、セルが互いに素な2つの環状鎖に分解できます。これらの四面体は4辺の長さを持ち、一方は右（時計回り）に螺旋状に、もう一方は左（反時計回り）に螺旋状に伸びています。左巻きと右巻きのセルリングは、互いに嵌合し、入れ子状になり、16セル全体を埋め尽くしますが、キラリティは逆です。この分解は、16セルの4-4デュオアンチプリズム構造に見られます。または、シュレーフリ記号{2}⨂{2} または s{2}s{2}、対称性[4,2 + ,4]、次数 64。

3 本の 8 辺のパス (異なる色) が各 8 セル リングに沿って螺旋状になっており、各頂点で 90° の角度をなしています (リングに曲げられる前の Boerdijk–Coxeter らせんでは、異なるパスの角度は異なりますが、90° ではありません)。3 本のパス (3 つの異なる色と見かけの角度) が各頂点を通過します。らせんがリングに曲げられると、各 8 辺のパスのセグメント (さまざまな長さ) が両端を結合し、4𝝅 の片側円周に沿って長さ 8 辺、幅 1 辺のメビウスの帯を形成します。[ o ] 3 本の 8 辺のパスの 6 つの 4 辺の半分はそれぞれ 4 つの 90° の角度をなしていますが、 6 つの直交する大きな正方形ではありません。これらは端が開いた正方形で、端が反対側の頂点である 4 辺の 360° らせんです。 4つの辺は4つの異なる大正方形から派生しており、互いに直交している。同じカイラリティを持つペアを端から端まで繋げると、6つの4辺の経路は3つの8辺のメビウスループ、すなわち螺旋状の八角形を形成する。各八角形は、16セルのペトリー多角形であると同時に、16セルの異なる等傾斜回転の1つにおいて、8つの頂点すべてが一緒に回転する螺旋状の軌道でもある。[ v ]

同じ斜八角形の5つの見方[ w ]
エッジパスペトリー多角形[ 18 ]16セル 離散ファイブレーション直径弦
八芒星{8/3} [ 19 ]八芒星{8/1}コクセター飛行機B4八卦{8/2}=2{4}八卦{8/4}=4{2}
等傾斜線の端の軌跡の8本の√2弦。 [ x ]8つの√2辺を持つ斜め八角形。16セルには、この8頂点回路が3つあります。 すべての 24 √ 2エッジと 4 つの√ 4直交軸。 完全に直交する（互いに素な） 2辺の正方形2つ。[ f ]等傾斜線の4本の√4弦。等傾斜線の4つの頂点は、16セル軸によってその対蹠頂点と結ばれている。[ x ]

8辺の螺旋はそれぞれ、16​​セルの周りを3回巻き、すべての頂点を通過してからループを形成する斜めの八角形{8/3}です。8つの√2辺は、等傾斜線（8つの頂点が等傾斜回転中に回転する螺旋状の弧）の弦です。[ o ] 16セルの8つの頂点はすべて√2離れていますが、反対側の頂点（対蹠頂点）は√4離れています。等傾斜線上を移動する頂点は、 √4離れた4番目の頂点に到達する前に、√2離れた他の3つの頂点を通過します。[ n ]

8セルリングはキラルである。つまり、時計回りに螺旋する右巻き型と反時計回りに螺旋する左巻き型が存在する。16セルリングにはそれぞれ1つずつ含まれているため、左右の等傾斜線も存在する。等傾斜線とは、8セルリングが回転する円軸である。各等傾斜線は、16セルリングの8つの頂点すべてを通過する。[ aa ]各8セルリングには16セルの半分が含まれるが、8つの頂点はすべて通過する。2つのリングは頂点を共有しており、互いに入れ子になってフィットする。また、左と右の八角形ヘリックスはそれぞれ異なる8辺の経路を持つが、24辺も共有している。[ ab ]

完全に直交する大正方形が3組あるため、[ c ] 2つの8セルリングから16セルを構成する3つの合同な方法があります。16セルには、異なる方向にある左右3組の8セルリングが含まれており、各セルリングにはその軸等傾斜線が含まれています。[ v ]左右の各等傾斜線は、左右の異なる等傾斜回転の軌跡です。等傾斜回転とは、完全に直交する不変回転面の1組における回転です。[ f ]各頂点には、3つの大正方形と、頂点で交差し16セルの軸弦を共有する6つの八角形等傾斜線があります。[ ac ]

構成として

この配置行列は16個のセルを表します。行と列は頂点、辺、面、セルに対応します。対角の数字は、各要素が16個のセル全体にいくつ出現するかを示します。非対角の数字は、列の要素が行の要素内またはその位置でいくつ出現するかを示します。

[86128224443332246416]{\displaystyle {\begin{bmatrix}{\begin{matrix}8&6&12&8\\2&24&4&4\\3&3&32&2\\4&6&4&16\end{matrix}}\end{bmatrix}}}

テッセレーション

4次元ユークリッド空間を正16セルでモザイク状に分割することができます。これは16セルハニカムと呼ばれ、シュレーフリ記号{3,3,4,3}で表されます。したがって、16セルの二面角は120°です。[ 21 ]各16セルは、正四面体を共有する隣接セルが16個、辺のみを共有する隣接セルが24個、点のみを共有する隣接セルが72個あります。このモザイク状の任意の頂点には、24個の16セルが接しています。

双対の24セルハニカム{3,4,3,3}は、正24セルで構成されています。テッセラティックハニカム{4,3,3,4}と合わせて、R 4の正則なテッセレーションは3つしかありません。

予測

正投影図
コクセター飛行機B4​B 3 / D 4 / A 2B 2 / D 3
グラフ
二面対称性[8] [6] [4]
コクセター飛行機 F4​A3​
グラフ
二面対称性 [12/3] [4]
16セルの投影エンベロープ。（各セルは異なる色の面で描画され、反転したセルは描画されません）

16セルを3次元空間にセル優先で平行投影すると、立方体の外皮が形成されます。最も近いセルと最も遠いセルは、立方体内の内接四面体に投影されます。これは、正四面体を立方体に内接させる2通りの方法に対応しています。これらの四面体のそれぞれを囲むように、4つの他の（非正則な）四面体体積が配置され、それらは周囲の4つの四面体セルの像であり、内接四面体と立方体の間の空間を埋めています。残りの6つのセルは、立方体の正方形の面に投影されます。この16セルの投影では、すべての辺が立方体の外皮の面上にあります。

16セル断面のセルファースト平行投影

16セルを3次元空間に投影したセルファースト透視投影は、三角正四面体の外殻を持ちます。この外殻内のセルの配置は、セルファースト平行投影の場合と類似しています。

16セルを3次元空間に頂点優先で平行投影すると、正八面体の外殻を持つ。この正八面体は、座標平面に沿って切断することで、8つの正四面体の体積に分割できる。これらの体積はそれぞれ、16​​セル内の2つのセルの像である。16セルの観察者に最も近い頂点は、正八面体の中心に投影される。

最後に、エッジファースト平行投影には短縮された八面体のエンベロープがあり、面ファースト平行投影には六角形両錐体のエンベロープがあります。

4球のベン図

16 セルの 3 次元投影と 4 つの交差球 ( 4 セットのベン図) は位相的に同等です。

交差する球の数（0から4）で並べられた16個のセル     （すべてのセルとk面を参照）
4球のベン図と16セル投影を同じ方向に表示

対称構造

16 セルの対称群はB 4と表記されます。

16セルの対称性の低い形式は、デミテッセラクトまたは4デミキューブと呼ばれ、デミハイパーキューブファミリーのメンバーであり、h{4,3,3}とコクセター図で表される。または四面体セルを 交互に配置して 2 色で描くこともできます。

対称性の低い形では、2つの平行な四面体が双対配置で連結され、8つの（場合によっては細長い）四面体で接続された四面体反プリズムとして見られる。これはs{2,4,3}とコクセター図で表される。。

これは、s{2 1,1,1 }で表されるスナブ4直交座標とコクセター図としても見ることができます。または。

四次元立方体が4-4デュオプリズムとして構築されている場合、16 セルはその双対である 4-4デュオピラミッドとして考えることができます。

名前 コクセター図シュレーフリ記号コクセター記法注文 頂点図形
通常の16セル {3,3,4} [3,3,4]384
デミテッセラクト準正則16細胞 ＝＝h{4,3,3} {3,3 1,1 } [3 1,1,1 ] = [1 + ,4,3,3]192
交互4-4デュオプリズム2秒{4,2,4} [[4,2 + ,4]]64
四面体反プリズム s{2,4,3} [2 + ,4,3]48
交互四角柱プリズム sr{2,2,4} [(2,2) + ,4]16
スナブ4-オルソトープ＝s{2 1,1,1 } [2,2,2] + = [2 1,1,1 ] +8
4-銃器
{3,3,4} [3,3,4]384
{4}+{4} または 2{4} [[4,2,4]] = [8,2 + ,8]128
{3,4}+{ } [4,3,2]96
{4}+2{ } [4,2,2]32
{ }+{ }+{ }+{ } または 4{ } [2,2,2]16

メビウス・カントール多角形は正複素多角形3 {3} 3であり、は16セルと同じ頂点を共有しています。8つの頂点と8つの3辺を持ちます。[ 22 ] [ 23 ]C2{\displaystyle \mathbb {C} ^{2}}

正複素多角形2 {4} 4、は、4次元空間における8頂点、16辺（16辺の半分）の16セルとして実数表現される。その対称性は4 [4] 2、位数32である。 [ 24 ]C2{\displaystyle \mathbb {C} ^{2}}

2 {4} 4多角形 の正投影図
B 4コクセター平面では、2 {4} 4には 8 つの頂点と 16 個の 2 辺があり、ここでは 4 セットの色で表示されています。 8つの頂点は2つのセット（赤と青で表示）にグループ化され、各セットの頂点は他のセットの頂点とのみ辺で接続されており、この多角形は完全な二部グラフ、K 4,4を形成します。[ 25 ]

正16セルとテッセラクトは、同じB 4対称性を持つ15個の一様4次元多面体の正則な要素です。16セルは、D 4対称性を持つ一様多面体の一つでもあります。

16 セルは、立方ハニカム、4 次十二面体ハニカム、4 次六角形タイリングハニカムとも関連があり、これらはすべて八面体の頂点図形を持ちます。

これは、正四面体胞を持つ{3,3,p}四次元多面体の列に属する 。この列には、ユークリッド四次元空間の3つの正四次元多面体、 5胞体{3,3,3}、16胞体{3,3,4}、600胞体{3,3,5}、そして双曲空間の6次正四面体ハニカム{3,3,6}が含まれる。

これは、準正則多面体およびハニカムのシーケンスh{4,p,q}の最初のものであり、正則形式 {p,3,4} の半対称シーケンスです。

参照

2～10次元の基本凸正則多面体と一様多面体
家族アン​B nI 2 ( p ) / D nE 6 / E 7 / E 8 / F 4 / G 2H n
正多角形三角形四角p角形六角形五角形
均一な多面体四面体八面体•立方体デミキューブ十二面体•二十面体
均一ポリクロロンペンタコロン16セル• Tesseractデミテッセラクト24セル120セル• 600セル
一様5次元多面体5単体5-オルソプレックス• 5-キューブ5デミキューブ
一様6次元多面体6単体6-オルソプレックス• 6-キューブ6デミキューブ1 22 • 2 21
一様7次元多面体7単体7-オルソプレックス• 7-キューブ7デミキューブ1 32 • 2 31 • 3 21
一様8次元多面体8単体8-オルソプレックス• 8-キューブ8デミキューブ1 42 • 2 41 • 4 21
一様9次元多面体9単体9-オルソプレックス• 9-キューブ9デミキューブ
一様10次元多面体10単体10-オルソプレックス• 10-キューブ10デミキューブ
一様n多面体n -単体n -オルソプレックス• n -キューブn -デミキューブ1 k2 • 2 k1 • k 21n -五角形多面体
トピック:多面体族•正多面体•正多面体と複合多面体の一覧•多面体の演算

注記

  1. ^凸正4次元多面体は、同じ半径に対する4次元コンテンツ（超体積）の尺度として、サイズで順序付けることができます。シーケンス内の各大きな多面体は、前のものよりも丸みを帯びており、同じ半径内に多くのコンテンツ[ 5 ]を囲んでいます。4単体（5セル）が最小の場合で、120セルが最大です。複雑さ（配置行列の比較または単に頂点の数によって測定）も同じ順序に従います。これは、16セルが8点4次元多面体である正多面体の代替数値命名スキームを提供します。これは、5点4次元多面体から600点4次元多面体までの昇順シーケンスの2番目です。
  2. ^ 8 セル (テッセラクト) には 16 セルが 2 個しか内接せず、24 セルには 16 セルが 3 個しか内接せず、600 セルには 75 個の異なる 16 セル (ただし、分離した 16 セルは 15 個のみ) が内接し、120 セルには 675 個の異なる 16 セル (ただし、分離した 16 セルは 75 個のみ) が内接します。
  3. ^ a b c d e f 4 次元空間では、1 点を通る 4 本の垂直軸と 6 本の垂直平面を作成できます。一般性を失うことなく、これらを (w, x, y, z) デカルト座標系の軸と直交中心平面と見なすことができます。4 次元には、3 次元と同じ 3 つの直交平面 (xy、xz、yz) があり、さらに他の 3 つの直交平面 (wx、wy、wz) があります。6 つの直交平面のそれぞれは、他の 4 つの平面と軸を共有し、他の平面のうち軸を共有しない唯一の平面とのみ反対または完全に直交します。したがって、完全に直交する平面が 3 組あります。xy と wz は原点のみで交差し、xz と wy は原点のみで交差し、yz と wx は原点のみで交差します。
  4. ^ a b c 16セルの各頂点は八面体ピラミッドの頂点であり、その底面は頂点が辺で結ばれた他の6つの頂点によって形成される八面体である。16セルは、4つの八面体中心超平面の1つで半分に切断することにより、2つの八面体ピラミッドに分解できる（4つの異なる方法）。16個の面結合四面体からなる境界面の湾曲した3次元体積の内側から見ると、16セルの頂点図形は八面体である。4次元では、頂点八面体は実際には八面体ピラミッドである。八面体ピラミッドの頂点（6つの辺が交わる頂点）は、実際には八面体の中心ではありません。頂点は、八面体の6つの頂点によって定義される超平面から、4次元方向の外側に放射状にずれています。頂点の周りの6つの辺は、3次元方向（および4次元ピラミッドの3次元投影）において3軸直交交差を形成しますが、実際には3本の直線は4次元方向において頂点で交わるところで90度曲がっています。
  5. ^ 16セルの境界面は、16個の正四面体が面と面を接して（1つの周りに4つ）配置された有限の3次元空間です。これは閉じた、きつく曲がった（非ユークリッド）3次元空間であり、その内部では、4つの正四面体をどの方向にもまっすぐ通過し、出発点である正四面体に戻ることができます。この正四面体のジャングルジム内を動き回り、24本の支柱（辺）を使って正四面体から正四面体へと登っていく様子を想像してみてください。どの方向に進んでも（どの方向を見ても）、16個の正四面体から外に出る（または外を見る）ことはできません。私たちは常に16セルの表面上（または表面内）におり、16セル自体の内部（または外部）にいることはありません。各頂点の周りの6つの辺は3次元的に対称に放射状に広がり、八面体の半径と同じように直交する3軸の十字を形成していることがわかります（したがって、16セルの頂点図形は八面体であると言えます）。 [ d ]
  6. ^ a b c d完全に直交する大正方形は交差せず、独立して回転します。これは、その頂点がある大円がクリフォード平行であるためです。[ k ]これらは、最も近い頂点の各ペアで√ 2離れています (16 セルでは、対蹠ペア以外のすべてのペアが最も近いです)。2 つの正方形は、16 セルの中心という 1 点でのみ交差する平面上にあるため、まったく交差できません。[ c ]これらは垂直で、共通の中心を共有しているため、2 つの正方形は明らかに平行ではなく、3 次元で平行な正方形が通常どのように分離しているかを示しています。むしろ、隣接する正方形のリンクのようにチェーンで接続され、各リンクが他のリンクを通過しても交差しないため、ホップリンクを形成します。
  7. ^ a b 16 セル内の各頂点 (および反対の頂点) で 3 つの大きな正方形が交わる。それぞれの正方形には、完全に直交する異なる正方形がある。したがって、各頂点とその反対の頂点 (各軸) に完全に直交する 3 つの大きな正方形が存在する。それらは 1 つの正八面体 (中心超平面) を形成する。16 セル内のすべての軸線は、中央の正八面体超平面に完全に直交し、すべての大きな正方形平面は、別の大きな正方形平面に完全に直交している。[ c ]軸と正八面体は 1 点 (16 セルの中心) でのみ交差し、完全に直交する大きな正方形の各ペアは 1 点 (16 セルの中心) でのみ交差する。各中心の正八面体は、8 つの頂点のうち 2 つの正八面体頂点図形でもある。つまり、その完全に直交する軸上の 2 つの頂点である。
  8. ^ 16 セルの各頂点で交差する3 つの不完全直交大正方形は、頂点の八面体頂点図形を形成します。 [ d ]それらの 2 つと、3 つ目の完全に直交する正方形を組み合わせると、八面体、つまり中心八面体超平面が形成されます。 [ g ] 16 セルでは、各八面体頂点図形も中心八面体超平面です。
  9. ^各大正方形の頂点は、その正方形の他の2つの頂点から√2離れており、反対側の頂点からは√4離れている。16マス目の他の4つの頂点（これも√2離れている）は、その正方形の完全に直交する正方形の頂点である。 [ f ]各16マス目の頂点は、そこで交差する3つの直交する大正方形の頂点である各大正方形にはそれぞれ異なる完全に直交する正方形がある。したがって、各頂点には完全に直交する3つの大正方形、すなわちその頂点が属さない正方形が存在する。 [ h ]
  10. ^ a b c d各大正方形平面は 5 つの他の正方形平面と等斜線 (クリフォード平行) ですが、完全に直交するのはそのうちの 1 つの平面だけです。完全に直交する平面のすべてのペアにはクリフォード平行な大円がありますが、すべてのクリフォード平行な大円が直交しているわけではありません。また、完全に直交する平面がクリフォード平行面の特別なカテゴリに分類される別の理由もあります。それは、それらがキラルではないということです。等斜線 (クリフォード平行) 平面の​​ペアは、2つの角度が 90° (完全に直交する平面) または 0° (一致する平面) で離れていない限り、左ペアまたは右ペアになります。 [ 20 ]ほとんどの等斜面は、それぞれ左等斜回転または右等斜回転によってのみ結合されます。完全に直交する平面は特別です。平面のペアは左と右の両方のペアであるため、左または右の等斜回転で結合されます。 90°等傾斜回転によって分離された平面は180°離れているため、左側の平面と右側の平面は同じ平面です。[ q ]
  11. ^ a b cクリフォード平行線は交差しない曲線で、それらの間の垂直（最短）距離が各点で同じという意味で平行です。[ 7 ]二重らせんは、通常の 3 次元ユークリッド空間におけるクリフォード平行線の例です。 4 次元空間では、クリフォード平行線は3 次元球面上の測地線大円として現れます。[ 8 ] 16 セルでは、完全に直交する大円正方形の対応する頂点はすべて√ 2離れているため、これらの正方形はクリフォード平行多角形です。[ j ]大正方形の頂点（大円上の点）のみが√ 2離れていることに注意してください。正方形の辺（円の弦上）の点は互いに近くなっています。
  12. ^単位半径4次元多面体の反対側の頂点は、8セル超立方体（テッセラクト）の反対側の頂点に対応する。この放射状に正三角形状の4次元立方体の長対角線は√4である。90°等傾斜回転では、16セルの各頂点は、長さ 𝝅 (180°) の螺旋状の測地線に沿って、単位半径4次元多面体（16セルまたはテッセラクト）の長径に沿って√4離れた頂点まで移動し、その反対側の頂点まで移動する。これは、テッセラクトにおける4つの連続する直交辺に沿って√1を4回移動した場合と同じ移動量である。
  13. ^正方形の辺に沿って、対蹠頂点のペアを結ぶ2辺パスは6種類あります。左等斜回転はそのうち3つのパスの間を対角線状に走り、右等斜回転は残りの3つのパスの間を対角線状に走ります。これらの対角線は、それぞれ左手系8セル環と右手系8セル環において、面結合した四面体セルの反対側の頂点を結ぶ直線（測地線）です。
  14. ^ a b c 16セルにおいて、2つの対蹠頂点は、面結合した2つの四面体セルの反対側の頂点である。2つの対蹠頂点は、四面体セルの辺に沿った（3つの異なる）2辺大円経路、様々な3辺経路、そして等傾斜線とペトリー多角形上の4辺経路によって接続される。[ o ]
  15. ^ a b c d等傾斜線は、メビウスの輪で結ばれた2つのヴィラルソー円に対応する特殊な円です。2次元ではなく4次元にわたって曲線を描きます。通常の円の円周はすべて2𝝅ですが、16セルの等傾斜線は円周が4𝝅（90°弦8本分）の円です。等傾斜線は平面上にはない円ですが、混乱を避けるため、ここでは常に等傾斜線と呼び、平面上にある通常の円については円という用語を使用します。
  16. ^ a b等傾斜回転では、6 つの直交平面すべてが 2 つの直交方向に同時に変位します。つまり、同じ角度で回転し、同時に同じ角度で横に傾きます。等傾斜変位 (クリフォード変位とも呼ばれる) は 4 次元的に対角です。点は 4 つの直交方向に同時に等しい距離変位し、合計ピタゴラス距離はその距離の 2 乗の 4 の平方根に等しいです。正 4 次元多面体の頂点はすべて、少なくとも 2 辺の長さ離れた頂点に変位します。たとえば、単位半径 16 セルが大正方形不変平面内で等傾斜 90° 回転すると、完全に直交する大正方形不変平面内でも 90° 回転します。[ c ]大正方形平面も、完全に直交する平面を占めるために横に 90° 傾きます。 (等斜対称性により、すべての大正方形は 90° 回転し、完全に直交する平面内で 90° 横に傾きます。) すべての大正方形内の各頂点は、4 つの直交方向のそれぞれに√ 1の距離、合計で√ 4の距離だけ、その対蹠頂点まで移動します。[ l ]元の頂点と移動先の頂点は、大正方形の 2 つの辺に沿う3 つの[ m ]つの異なるパスによって 2 辺の長さだけ離れています。ただし、等斜線(等斜回転中に頂点がたどる螺旋状の弧) は辺に沿うのではなく、元の頂点と移動先の頂点の間の測地線 (最短の弧) 上を対角線上にこれらの異なる辺のパスの間を進みます。[ n ]この等斜測地線弧は通常の大円の一部ではなく、どの大正方形の平面にも存在しません。これは、2つの完全に直交する平面において同時に円弧を描く、螺旋状の180°円弧です。このメビウスの円は、元の頂点と変位した頂点の間のどの平面にも属さず、どの頂点とも交差しません。[ o ]
  17. ^ a b c 2つの完全に直交する平面を90度等傾斜回転させる場合、それらの平面は互いに接近する。16セルの剛体をこのように回転させる場合、6つの直交平面すべてが90度回転し、それらの完全に直交する（クリフォード平行）[ k ]平面に対して横に90度傾く。[ 9 ] 2つの完全に直交する大正方形の対応する頂点は√4 （ 180 °）離れている。大正方形（クリフォード平行多面体）は√4（180°）離れている。しかし、2つの完全に直交する平面は、それらを隔てる2つの直交角において90°離れている。等傾斜回転をさらに90°続けると、各頂点は360°回転し、各大正方形は元の平面に戻りますが、向きが異なります（軸が入れ替わります）。つまり、16セルの表面上で「上下逆さま」に回転したことになります（つまり、裏返しになったことになります）。さらに360°等傾斜回転（90°×90°の等傾斜回転を4回繰り返す、720°回転）を続けると、すべてが元の位置と向きに戻ります。
  18. ^オルソスキームとは、直角三角形の面を持つ不規則な単体であり、ある多面体を自身の面（鏡面壁）における自身の反射で正確に埋め尽くす場合に、その多面体の特性となる。すべての正多面体は、その中心を囲む特性オルソスキームのインスタンスへと放射状に分割することができる。特性オルソスキームは、生成点環を持たない正多面体と同じコクセター・ディンキン図で表される形状を持つ。
  19. ^ k次元の正多面体は特性k直交配位子と特性( k -1)直交配位子を持つ。4次元正多面体は、その(3次元)対称超平面によって分割される特性5セル(4直交配位子)と、その表面がセルの(2次元)対称面によって分割される特性四面体(3直交配位子)を持つ。その(3次元)表面を各セル中心を囲む特性四面体に分割した後、その(4次元)内部を、表面特性四面体の頂点と4次元多面体の中心を結ぶ半径を加えることで、特性5セルに分割できる。 [ 12 ]こうして形成される内部四面体と三角形も直交配位子となる。
  20. ^ a b ( Coxeter 1973 ) では、正多面体の3つの特性角𝟀、𝝓、𝟁 のいずれかを表すためにギリシャ文字 𝝓 (ファイ) が用いられています。𝝓 は黄金比定数 ≈ 1.618 を表すのに一般的に用いられますが、Coxeter はこの定数に � (タウ) を用いています。そこで、ここでは Coxeter の慣例を逆にし、特性角を表すのに � を用います。
  21. ^正 4 次元多面体の中心で交わる各 4 辺の長さは不等です。これは、正 4 次元多面体の 4 つの特性半径、つまり頂点半径、辺中心半径、面中心半径、セル中心半径が等しくないためです。4 次元多面体の 5 つの頂点には、常に 1 つの正 4 次元多面体の頂点、1 つの正 4 次元多面体の辺中心、1 つの正 4 次元多面体の面中心、1 つの正 4 次元多面体のセル中心、および正 4 次元多面体の中心が含まれます。これらの 5 つの頂点 (この順序で) は、互いに垂直な 4 辺 (3 回の直角ターン) に沿った経路を構成し、これが 4 次元多面体の特性です。4 次元多面体には、5 つの異なる 3 次元多面体ファセットがあります。
  22. ^ a b 16セルは、セルが互いに素な2つの8セルリングから3つの異なる方法で構築できます。つまり、リングのペアには3つの向きがあります。それぞれの向きには、左右の等傾斜回転のペアと、完全に直交する大正方形（クリフォード平行繊維）のペアが「含まれ」ているため、それぞれの向きは16セルの離散的なファイブレーションとなります。それぞれの8セルリングには、3つの離散的なファイブレーションにおいて異なる向き（役割が交換される）を持つ3つの軸八角形と、セルリングを通る6つの異なる等傾斜回転（左3つ、右3つ）が含まれます。単一のセルリングの図には、3つの八角形（異なる色）が見られます。1つはペトリー多角形の役割、1つは右等傾斜、1つは左等傾斜の役割です。それぞれの八角形が3つの役割を果たすため、16セルには18ではなく6つの異なる等傾斜が存在します。
  23. ^ 5つの図はすべて、16セルを同一平面（8セルの環状円筒の円形断面）に正射影したもので、上図の切断された環状円筒の中心軸に沿って円筒の一端から見ています。唯一の違いは、 √2辺と√4弦のうち、焦点を合わせるために省略されているものだけです。√2辺の色が異なるのは、観察者に対して斜めになっている角度が異なるためです。頂点には反時計回りに1（上）から8までの番号が付けられています。
  24. ^ a b各等傾斜線には、その八芒星{8/3}の辺経路の8 本の連続する√ 2弦と、八芒星の 4つ目の頂点ごとに接続しているが互いに接続していない 4 本の不連続な√ 4直径弦があります。対蹠頂点にも、それらを接続する 4 つの互いに直交する√ 2辺のねじれた連続経路があります。対蹠頂点間では、等傾斜線は辺経路の4 本の√ 2弦にわたってらせん状に滑らかにカーブし、介在する 3 つの頂点に当たります。各√ 2辺は、別の大正方形に完全に直交する大正方形の辺であり、その大正方形では√ 4弦が対角線になっています。
  25. ^ a b回転の左右の等傾斜線が同じ頂点集合を訪れる別の例として、5セルの等傾斜回転の特徴的な例を参照してください。これら2つの特殊なケースでは、同じ回転の左右の等傾斜線が同じ頂点集合を訪れますが、異なる順序で同じ頂点を訪れるため、回転経路は大きく異なります。
  26. ^ a b 5細胞と16細胞を除いて、[ y ]左右の等傾斜円のペアは頂点が分離しています。左右の等傾斜らせんは交差しない平行線ですが、逆回転しており、3次元では発生しない特殊な種類の二重らせんを形成します（同じ半径の逆回転らせんは交差する必要があります）。
  27. ^ a b 16セルでは、各等傾斜線は8つの頂点すべてを通って曲がりくねっており、2つの完全に直交する大きな正方形の完全な繊維化である。 [ j ] 5セルと16セルは、各離散繊維化が1つの等傾斜繊維のみを持つ唯一の正則4次元多面体である。[ z ]
  28. ^左等傾斜線と右等傾斜線はすべての頂点で交差する。これらは同じ8頂点の異なる列である。√2離れた4頂点ペアの集合に関してのみ、クリフォード平行とみなすことができる。√4離れた4頂点ペアの集合に関してのみ、それらは完全に直交しているとみなすことができる。 [ j ]
  29. ^これは一般に等傾斜回転では異例で、通常、左等傾斜と右等傾斜の両方が同じ頂点に現れることはありません。それぞれ左または右の回転でのみ到達可能な、互いに素な 2 つの頂点セットが存在します。 [ z ] 16 セルの左等傾斜と右等傾斜は、非常に特殊な二重らせんを形成します。これは単に円形であるだけでなく、異なる左および右のらせんが同じ対蹠頂点セットを介して互いの周りをねじれている点でも珍しいことです。 [ aa ]自然界で見られるほとんどの等傾斜回転で等傾斜のペアが行うように、対蹠頂点の2 つの互いに素なサブセットを介してねじれているのではありません。 [ y ]完全に直交する不変面での等傾斜回転は特別です。 [ j ]これらがなぜ特別なのかを確認するには、それぞれがある回転角度で回転し、同じ回転角度で横に傾いて完全に異なる平面になっている、2 つの完全に直交する不変回転面を視覚化します。 [ p ]回転角が90°の場合にのみ、傾き不変面が着地する別の平面は、完全に直交する不変面そのものです。回転の目的面は、完全に直交する不変面です。90°等傾斜回転は、完全に直交する不変面同士を近づける唯一の回転です。 [ q ]この相互性こそが、左回転と右回転の両方が同じ場所に到達する理由です。

引用

  1. ^ Coxeter 1973、p. 141、§ 7-x。歴史的考察。
  2. ^ NWジョンソン：幾何学と変換、（2018） ISBN 978-1-107-10340-5第11章有限対称群、11.5球面コクセター群、p.249
  3. ^マティラ・ギカ『芸術と人生の幾何学』（1977年）、68ページ
  4. ^ Coxeter 1973 , pp. 120–121, § 7.2. 図7.2Bを参照。
  5. ^ Coxeter 1973 , pp. 292–293, 表I(ii): 4次元における16個の正多面体 { p,q,r }。各4次元多面体の20個の計量すべてを辺の長さ単位で示す貴重な表。単位半径の多面体を比較するには、代数的に変換する必要がある。
  6. ^ Kim & Rote 2016、p. 6、§ 5. 4次元回転。
  7. ^ Tyrrell & Semple 1971、pp. 5–6、§ 3。Cliffordによる平行法の元の定義。
  8. ^ Kim & Rote 2016、pp. 7–10、§ 6. 4次元空間における2つの平面間の角度。
  9. ^ Kim & Rote 2016、pp. 8–10、クリフォード平行主義との関係。
  10. ^ Coxeter 1973 , p. 121, § 7.21. 図7.2Bを参照：「、（2つの頂点が4次元に沿って反対方向にある）に基づく4次元双錐体であるβ4{\displaystyle \beta _{4}}β3{\displaystyle \beta _{3}}
  11. ^ Tyrrell & Semple 1971 .
  12. ^ Coxeter 1973、p. 130、§ 7.6;「単体分割」。
  13. ^ Coxeter 1973、pp. 292-293、表I(ii)；「16セル、𝛽 4」。
  14. ^ Coxeter 1973、p. 139、§ 7.9 特性単体。
  15. ^ Coxeter 1973、p. 290、表I(ii)；「二面角」。
  16. ^ Coxeter 1970、p. 45、表2：反射ハニカムとそのグループ。ハニカム[3,3,4] 4は、8つの四面体セルの2つのリングによる3次元球面のタイリングです。
  17. ^バンチョフ 2013 .
  18. ^ Coxeter 1973、pp. 292-293、表I(ii); 24セルh 1。
  19. ^ Coxeter 1973、pp. 292-293、表I(ii)；24セルh 2。
  20. ^ Kim & Rote 2016、pp. 7–8、§ 6 4次元空間における2つの平面間の角度、等斜面の左右のペア。
  21. ^コクセター 1973、293ページ。
  22. ^コクセター 1991、30、47頁。
  23. ^コクセター＆シェパード 1992 .
  24. ^コクセター 1991、108ページ。
  25. ^コクセター 1991、114ページ。

参考文献

ウィキバーシティには16細胞に関する学習リソースがあります
「 https://en.wikipedia.org/w/index.php?title=16-cell&oldid=1303765587」より取得