二三角多面体
幾何学では、二三角多面体と呼ばれる7つの均一な双対多面体があります。[ 1 ]
二角形頂点図形
5つの均一な二面体多面体があり、すべて二十面体対称性を持っています。[ 1 ]
3 | p qまたはの形で表されるウィトフ記号を持つ3つの均一な星型多面体3/2 | p qは、少なくともpとq が2 でない場合は、二重三角面です。各多面体には、三角形、五角形、五芒星形の 2 種類の面が含まれます。頂点の配置は、 p . q . p . q . p . qまたは ( p . q ) 3の形をとり、対称性は 3 次です。ここで、二重三角面という用語は、頂点図形の 6 つの角度に対して 2 つの回転軌道で作用する、対称性 3 次 (三角形対称) の六角形を指します (二重三角面という語は「3 つの角度の組が 2 つある」という意味です)。[ 2 ]
| タイプ | 小さな二三角二十面体 | 二方正十二面体 | 大二三角二十面体 |
|---|---|---|---|
| 画像 |  |  |  |
| 頂点図形 |  |  |  |
| 頂点構成 | 3. 5 ⁄ 2 .3. 5 ⁄ 2 .3. 5 ⁄ 2 | 5. 5 ⁄ 3 .5. 5 ⁄ 3 .5. 5 ⁄ 3 | (3.5.3.5.3.5)/2 |
| 顔 | 32 20 {3}, 12 { 5 ⁄ 2 } | 24 12 {5}, 12 { 5 ⁄ 2 } | 32 20 {3}, 12 {5} |
| ウィトフ記号 | 3 | 5/2 3 | 3 | 5/3 5 | 3 | 3/2 5 |
| コクセター図 | 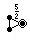 | 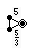 | 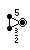 |
その他の均一な二三角多面体
小さな二三角十二面体と大きな二三角十二面体も均一です。
それらの双対はそれぞれ小二三角十二六十面体と大二三角十二六十面体である。[ 1 ]
参照
参考文献
注記
- ^ a b cハレル、1993
- ^ Uniform Polyhedron、Mathworld(2016年6月10日閲覧)
参考文献
- Coxeter, HSM、MS Longuet-Higgins、JCP Miller、「Uniform Polyhedra」、Phil. Trans. 246 A (1954) pp. 401–450。
- Har'El, Z. Uniform Solution for Uniform Polyhedra. , Geometriae Dedicata 47, 57–110, 1993. Zvi Har'El , Kaleido software , Images , dual images