ワームホール
ワームホールを2次元面として視覚化したもの。経路(a)は点1と点2の間の通常空間を通る最短経路であり、経路(b)はワームホールを通るより短い経路である。

ワームホールとは、時空における異なる点を結ぶ仮説上の構造である。時空における異なる点（すなわち、異なる場所、異なる時点、あるいはその両方）に両端を持つトンネルとして視覚化することができる。ワームホールは、アインシュタインの場の方程式の特殊解に基づいている。[ 1 ]ワームホールは一般相対性理論 と整合しているが、実際に存在するかどうかは不明である。多くの物理学者は、ワームホールは単に4次元空間の投影に過ぎないと仮定している。これは、 2次元（2D）の存在が3次元（3D）物体の一部しか体験できないのと同様である。[ 2 ]

1995年、マット・ヴィッサーは、初期宇宙で負の質量を持つ宇宙ひもが生成された場合、宇宙には多数のワームホールが存在する可能性があると示唆した。[ 3 ] [ 4 ]キップ・ソーンなどの物理学者は、ワームホールを人工的に作成する方法を提案している。[ 5 ]

用語

1928年、ドイツの数学者、哲学者、理論物理学者であるヘルマン・ワイルは、電磁場エネルギーの質量分析に関連して、物質のワームホール仮説を提唱した。 [ 6 ] [ 7 ]しかし、彼は「ワームホール」という用語は使わなかった（代わりに「1次元チューブ」という言葉を使った）。[ 8 ]

アメリカの理論物理学者ジョン・アーチボルド・ウィーラーは（ワイルの研究に触発されて）[ 8 ]「ワームホール」という用語を造語した。[ 9 ] [ 10 ] [ 11 ] 1957年にチャールズ・W・ミスナーと共著した論文の中で、彼らは次のように述べている。[ 12 ]

この分析により、位相学者が「多重連結空間のハンドル」と呼ぶもの、そして物理学者ならより鮮明に「ワームホール」と呼んでも許されるようなものを通る、力線の正味の流れがある状況について考える必要が出てきます。

— チャールズ・マイズナーとジョン・ウィーラー著『Annals of Physics』

現代の定義

ワームホールは幾何学的にも位相的にも定義されてきました。位相的な観点から見ると、宇宙内ワームホール（同一宇宙内の2点間のワームホール）とは、境界は位相的に自明であるものの、内部が単純連結ではないコンパクトな時空領域です。この概念を形式化すると、マット・ヴィッサーの『ロレンツ型ワームホール』（1996年）から引用した以下のような定義が導き出されます。 [ 13 ]

ミンコフスキー時空にコンパクト領域 が含まれ、 の位相がの形式である場合( は非自明な位相の3 次元多様体であり、その境界は の形式の位相を持ち、さらに超曲面がすべて空間的である場合、領域には準永久的な宇宙内ワームホールが含まれます。Ω{\displaystyle \オメガ}Ω{\displaystyle \オメガ}Ω〜S×Σ{\displaystyle \Omega \sim {S}\times \Sigma }Σ{\displaystyle \Sigma }δΣ〜S2{\displaystyle \delta \Sigma \sim {S^{2}}}Σ{\displaystyle \Sigma }Ω{\displaystyle \オメガ}

幾何学的には、ワームホールは閉曲面の漸進的変形を制限する時空領域として記述できます。例えば、エンリコ・ロドリゴの『スターゲイトの物理学』では、ワームホールは以下のように非公式に定義されています。

世界線（点または観測者の時間的発展）まで連続的に変形（縮小）できない「世界管」（閉じた表面の時間的発展）を含む時空領域。

発達

シュワルツシルトワームホールの「埋め込み図」

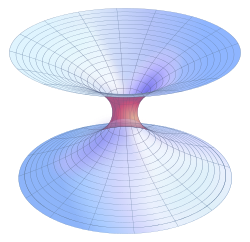
シュワルツシルトワームホール

最初に発見されたワームホールの解はシュワルツシルトワームホールで、これは永遠のブラックホールを記述するシュワルツシルト計量に存在するが、あまりに速く崩壊し、端から端まで何かが渡ることができないことが判明した。両方向に横断できるワームホールは通過可能なワームホールとして知られ、負のエネルギー密度を持つエキゾチック物質を使用して安定化できる場合にのみ可能であると考えられていた。 [ 14 ]その後、物理学者は、微視的な通過可能なワームホールが可能であり、エキゾチック物質を必要とせず、荷電ブラックホールに崩壊しないほど十分に小さい質量を持つ帯電フェルミオン物質のみを必要とすると報告した。[ 15 ] [ 16 ] [ 17 ]このようなワームホールは、もし可能であれば、情報の転送に限定されるかもしれないが、現実が弦理論と一致するブレーンベースの理論であるランドール・サンドラムモデル2によって広く記述できる場合、人間が通過できるワームホールが存在する可能性がある。[ 18 ] [ 19 ]

アインシュタイン・ローゼン橋

アインシュタイン・ローゼン橋（ER橋ともいう） [ 20 ]は、アルバート・アインシュタインとネイサン・ローゼン[ 21 ]にちなんで名付けられ、アインシュタイン場の方程式の真空解としてモデル化できる空間領域間の接続であり、現在では電荷も回転もない永遠のブラックホールを記述するシュワルツシルト計量の最大限に拡張されたバージョンの本質的な部分であると理解されている。ここで「最大限に拡張された」とは、時空がいかなる「端」も持たないという考えを指す。つまり、自由落下する粒子のあらゆる軌道（時空の 測地線に従う）について、この経路を粒子の未来または過去に向かって任意に遠くまで続けることが可能であるべきである。

この要件を満たすためには、事象の地平線を外側から落下する粒子が入り込むブラックホール内部領域に加えて、事象の地平線から上昇していく粒子の軌道を外挿できる、独立したホワイトホール内部領域が存在する必要があることが判明しました。 [ 22 ]そして、最大限に拡張された時空に2つの独立した内部領域があるように、2つの異なる「宇宙」と呼ばれることもある2つの独立した外部領域があり、この2つの宇宙によって、2つの内部領域における粒子の軌道を外挿することができます。つまり、ブラックホール内部領域には、どちらの宇宙から落ちてきた粒子が混在する可能性があり（したがって、一方の宇宙から落ちてきた観測者は、もう一方の宇宙から落ちてきた光を見ることができるかもしれません）、同様に、ホワイトホール内部領域からの粒子はどちらの宇宙にも逃げ出すことができます。これら4つの領域はすべて、クラスカル・シェケレス座標を用いた時空図で見ることができます。

この時空においては、一定時間の超曲面（すべての点が同じ時間座標を持ち、面上のすべての点が空間的な間隔を持ち、「空間的面」と呼ばれるものを与える点の集合）を選び、その時間における空間の曲率を表す「埋め込み図」を描くと、埋め込み図は2つの外部領域を結ぶ管のように見え、「アインシュタイン・ローゼン橋」として知られる。シュワルツシルト計量は、外部観測者の観点から永遠に存在する理想的なブラックホールを記述する。より現実的なブラックホールは、ある特定の時間に崩壊する恒星から形成されるため、異なる計量が必要となる。ブラックホールの地形図に落下する恒星物質を加えると、ホワイトホール内部領域に対応する部分と、もう一方の宇宙に対応する部分が除去される。[ 23 ]

アインシュタイン・ローゼン橋は、シュヴァルツシルトが解を発表した数か月後の1916年にルートヴィヒ・フラムによって発見され、 [ 24 ] 、アルバート・アインシュタインと彼の同僚のネイサン・ローゼンによって再発見され、1935年にその結果が発表されました。 [ 21 ] [ 25 ] 1962年に、ジョン・アーチボルド・ホイーラーとロバート・W・フラーは、このタイプのワームホールは同じ宇宙の2つの部分を接続している場合は不安定であり、一方の外部領域から落ち込む光（または光より遅く移動する粒子）がもう一方の外部領域に到達するには速すぎる速度で切断されることを示す論文を発表しました。

一般相対性理論によれば、十分にコンパクトな質量の重力崩壊は、特異なシュワルツシルトブラックホールを形成する。しかし、アインシュタイン・カルタン・シアマ・キブル重力理論では、通常のアインシュタイン・ローゼン橋を形成する。この理論は、アフィン接続の対称性の制約を取り除き、その反対称部分であるねじれテンソルを動的変数と見なすことで、一般相対性理論を拡張する。ねじれは、量子力学的に物質の固有の角運動量（スピン）を自然に説明する。ねじれとディラックスピノル間の最小限の結合は、極めて高密度のフェルミオン物質において顕著な反発スピン間相互作用を生成する。このような相互作用は、重力特異点（例えばブラックホール）の形成を妨げる。代わりに、崩壊する物質は巨大だが有限の密度に達して跳ね返り、橋の反対側を形成する。[ 27 ]

シュワルツシルトワームホールは双方向に通過可能ではないが、その存在に触発されてキップ・ソーンは、シュワルツシルトワームホールの「喉」をエキゾチック物質（負の質量/エネルギーを持つ物質）で開いたままにすることで通過可能なワームホールを想像した。[ 28 ]

その他の通過不可能なワームホールには、ローレンツワームホール（1957年にジョン・アーチボルド・ホイーラーによって初めて提案された）、ローレンツ多様体によって描かれた一般相対論的時空多様体内に時空泡を形成するワームホール、[ 29 ]、ユークリッドワームホール（リーマン多様体の構造であるユークリッド多様体にちなんで名付けられた）がある。[ 30 ]

通過可能なワームホール

カシミール効果は、量子場の理論では、空間の特定の領域でエネルギー密度が通常の物質の真空エネルギーに対して負になることが許容されるが、量子場の理論では、エネルギーが任意の時間長に対して任意の負になる状態は許容されないことが理論的に示されている。 [ 31 ] [ 32 ]スティーブン・ホーキング、[ 33 ]キップ・ソーン、[ 34 ]その他、[ 35 ]などの物理学者の中には、このような効果によって通過可能なワームホールを安定化できる可能性があると主張した。[ 36 ]一般相対性理論と量子力学の文脈で理論的にワームホールを形成すると予測される唯一の既知の自然プロセスは、フアン・マルダセナとレナード・サスキンドのER = EPR予想で提唱されたものである。量子泡仮説は、プランクスケールで微小なワームホールが自発的に現れては消滅する可能性があることを示唆するために時々使用される[ 37 ]：494-496 [ 38 ]そしてそのようなワームホールの安定したバージョンが暗黒物質の候補として示唆されてきた。[ 39 ] [ 40 ]また、負の質量の宇宙ひもによって開いたままになっている微小なワームホールがビッグバンの頃に現れていたとしたら、宇宙インフレーションによって巨視的サイズにまで膨らんだ可能性があると提案されている。[ 41 ]

テュービンゲン大学物理学研究所前の広場とフランス北部ブローニュ＝シュル＝メール近郊の砂丘を結ぶ、通過可能なワームホールのシミュレーション画像。この画像は、モリス＝ソーン・ワームホール計量を用いた4次元レイトレーシングによって計算されているが、光の波長に対する重力の影響はシミュレーションされていない。[注 1 ]

ロレンツ通過可能ワームホールは、宇宙のある部分から同じ宇宙の別の部分への双方向の移動を非常に高速に可能にするか、またはある宇宙から別の宇宙への移動を可能にします。一般相対論における通過可能なワームホールの可能性は、ホーマー・エリスによる1973年の論文[ 42 ]で初めて実証され、独立にKA・ブロニコフによる1973年の論文[ 43 ]でも実証された。エリスはエリス・ドレインホールの位相と測地線を解析し、それが測地線的に完全で、地平線がなく、特異点がなく、両方向に完全に通過可能であることを示した。ドレインホールは、真空時空におけるアインシュタインの場の方程式の解多様体であり、リッチテンソルに最小限に結合し、反正統的な極性（正ではなく負）を持つスカラー場を組み込むことで修正されている。 （エリスは、スカラー場を「エキゾチック」と呼ぶことを、非正統的な結合を理由に明確に拒否し、そうする論拠は説得力に欠けると判断した。）解は2つのパラメータに依存する。mは重力場の強度を決定し、nは空間断面積の曲率を決定する。mを0に設定すると、排水孔の重力場は消滅する。残るのはエリスワームホール、すなわち重力を持たず、純粋に幾何学的な、通過可能なワームホールである。

キップ・ソーンと大学院生のマイク・モリスは1988年に独立にエリスワームホールを発見し、一般相対性理論の教育ツールとしての利用を主張した。[ 44 ]このため、彼らが提案した球状の殻で開いた状態の通過可能なワームホールは、モリス・ソーンワームホールとも呼ばれる。

その後、一般相対性理論の方程式の許容解として、他のタイプの通過可能なワームホールが発見された。その中には、1989年のマット・ヴィッサーの論文で解析された多様体も含まれ、この多様体では、通過経路がエキゾチック物質の領域を通過しない場合でもワームホールを通過できる。しかし、純粋なガウス・ボネ重力（ブレーン宇宙論の文脈で研究されることもある、余分な空間次元を伴う一般相対性理論の修正）では、ワームホールの存在にエキゾチック物質は必要なく、物質がなくてもワームホールは存在できる。[ 45 ]負の質量を持つ宇宙ひもによって開いたままになるタイプが、ヴィッサーとクレイマーらの共同研究で提唱され、[ 41 ]その中で、そのようなワームホールは初期宇宙で自然に生成された可能性があると提案された。

ワームホールは時空上の2点を結ぶため、原理的には空間だけでなく時間も移動できる。1988年、モリス、ソーン、ユルトセバーは、ワームホールの2つの開口部のうち1つを加速させることで、空間を移動するワームホールを時間移動するワームホールに変換する方法を考案した。 [ 34 ]しかし、一般相対性理論によれば、ワームホールが初めてタイムマシンに変換された時点よりも前の時点にワームホールを使って移動することは不可能である。それまで、ワームホールは注目されることも、利用されることもなかったはずである。[ 37 ] : 504

レイチャウドゥリの定理とエキゾチック物質

なぜエキゾチック物質が必要なのかを理解するために、測地線に沿って進み、ワームホールを横切って反対側で再膨張する入射光の前面を考えてみましょう。膨張は負から正へと変わります。ワームホールの首は有限の大きさなので、少なくとも首の付近では、コースティックスが発生することは予想されません。光学的なレイショードリの定理によれば、これには平均ヌルエネルギー条件の違反が必要です。カシミール効果などの量子効果は、曲率がゼロの空間のどの近傍でも平均ヌルエネルギー条件に違反することはできませんが、[ 46 ]半古典的重力の計算では、曲がった時空では量子効果がこの条件に違反できる可能性があることが示唆されています。[ 47 ]最近、量子効果は平均ヌルエネルギー条件の非時系列バージョンに違反できないと期待されていましたが、[ 48 ]違反も見つかっており、[ 49 ]量子効果がワームホールをサポートするために使用される可能性が残っています。

修正一般相対性理論

一般相対論を修正したいくつかの仮説では、エキゾチック物質に頼ることなく崩壊しないワームホールが存在する可能性がある。例えば、f ( R )重力の一種であるR 2重力ではこれが可能である。[ 50 ]

光速を超える旅行

NASA のためにレス・ボシナが構想したワームホール旅行 レス・ボシナ (Cortez III Service Corp.) によるデジタルアート、1998 年
NASAのためにレ・ボッシナスが構想したワームホール旅行、 1998年頃

光速を超える相対速度の不可能性は、局所的にのみ適用されます。ワームホールは、局所的に光速を超えないことを保証することで、効果的な超光速（光速超）移動を可能にする可能性があります。ワームホールを通過する際は、光速以下の速度が使用されます。2点がワームホールで接続されており、その長さがワームホール外の2点間の距離よりも短い場合、ワームホールを通過するのにかかる時間は、光線がワームホール外の空間を通過するのにかかる時間よりも短くなる可能性があります。同じワームホールを通過する光線は、依然として移動者よりも速くなります。

タイムトラベル

もし通過可能なワームホールが存在するならば、タイムトラベルが可能になるかもしれない。[ 34 ]通過可能なワームホールを用いたタイムトラベルマシンの提案は、仮説的には以下のように動作する。ワームホールの一方の端を、おそらく何らかの高度な推進システムを用いて光速のかなりの割合まで加速し、その後、起点に戻す。あるいは、ワームホールの一方の入口を、​​もう一方の入口よりも重力が大きい物体の重力場内に移動し、その後、もう一方の入口の近くに戻すという方法もある。どちらの方法においても、時間の遅れにより、移動されたワームホールの端は、外部の観測者から見た静止した端よりも老化が遅くなる、つまり「若くなる」。しかし、ワームホール内と外部では時間の繋がり方が異なるため、ワームホールの両端にある同期した時計は、両端がどのように移動しても、ワームホールを通過する観測者から見ると常に同期したままである。[ 37 ] : 502 これは、「若い」端に入った観測者が「古い」端から「若い」端と同じ年齢の時に出て行くことを意味し、外部からの観測者から見ると事実上、時間を遡ることになります。このようなタイムマシンの大きな制約の一つは、機械が最初に作られた時点までしか遡ることができないことです。[ 37 ] : 503 これは、それ自体が時間を移動する装置というよりも、むしろ時間を通る道であり、技術自体を過去に遡らせることはできません。[ 51 ] [ 52 ]

ワームホールの性質に関する現在の理論によれば、通過可能なワームホールの構築には、負のエネルギーを持つ物質（しばしば「エキゾチック物質」と呼ばれる）の存在が必要となる。より技術的には、ワームホール時空は、ヌルエネルギー条件、弱エネルギー条件、強エネルギー条件、支配的エネルギー条件など、様々なエネルギー条件に違反するエネルギー分布を必要とする。量子効果によってヌルエネルギー条件がわずかに測定可能な程度に違反することが知られており、 [ 13 ] : 101 、多くの物理学者は、量子物理学におけるカシミール効果によって、必要な負のエネルギーは実際に可能であると考えている。[ 53 ]初期の計算では非常に大きな負のエネルギーが必要であると示唆されていたが、その後の計算では、負のエネルギーの量は任意に小さくできることが示された。[ 54 ]

1993年、マット・ヴィッサーは、このように誘起された時計差を持つワームホールの二つの開口部は、量子場と重力効果を誘起することなく接近させることはできないと主張した。その効果は、ワームホールを崩壊させるか、二つの開口部が互いに反発するかのいずれかであり、[ 55 ]あるいはワームホールを通過する情報の通過を妨げる。[ 56 ]このため、二つの開口部は因果律の破れが起こるほど近づけることができなかった。しかし、1997年の論文でヴィッサーは、N個のワームホールを対称多角形に配置した複雑な「ローマンリング」（トム・ローマンにちなんで名付けられた）構成は、依然としてタイムマシンとして機能する可能性があると仮説を立てた。ただし、これは因果律の破れが可能であることを証明するものではなく、古典的な量子重力理論の欠陥である可能性が高いと結論付けている。[ 57 ]

宇宙旅行

ワームホールを利用したタイムトラベルから生じるパラドックスの解決策は、量子力学の多世界解釈にかかっています。

1991年、デイヴィッド・ドイチュは、量子論が閉じた時間的曲線を持つ時空において完全に無矛盾であることを示した（いわゆる密度行列が不連続性から解放されるという意味で）。[ 58 ]その後、このような閉じた時間的曲線のモデルは内部矛盾を持つ可能性があり、非直交量子状態の区別や適切な混合と不適切な混合の区別といった奇妙な現象につながることが示された。[ 59 ] [ 60 ]したがって、半古典的計算によって示唆された、ワームホールタイムマシンを循環する仮想粒子の破壊的な正のフィードバックループは回避される。未来から帰還する粒子は、元の宇宙ではなく、並行宇宙に戻る。これは、極めて短い時間ジャンプを持つワームホールタイムマシンが、同時期の並行宇宙間の理論的な橋渡しとなることを示唆している。[ 14 ]

ワームホールタイムマシンは量子論に一種の非線形性を導入するため、並行宇宙間のこの種の通信は、スティーブン・ワインバーグの非線形量子力学の定式化におけるジョセフ・ポルチンスキーのエヴェレット電話[ 61 ]（ヒュー・エヴェレットにちなんで名付けられた）の提案と一致している。 [ 62 ]

並行宇宙間の通信の可能性は宇宙間旅行と呼ばれています。[ 63 ]

ワームホールは、シュワルツシルト・ブラックホールのペンローズ図にも描かれます。ペンローズ図では、光速を超える物体はブラックホールを横切り、別の端から別の空間、時間、または宇宙へと飛び出します。これは宇宙間ワームホールとなります。

メトリクス

ワームホール計量の理論は、ワームホールの時空幾何学を記述し、タイムトラベルの理論モデルとして機能する。（通過可能な）ワームホール計量の例としては、以下のものがある：[ 64 ]

ds2＝−c2dt2+dℓ2+（け2+ℓ2）（dθ2+罪2⁡θdφ2）、{\displaystyle ds^{2}=-c^{2}\,dt^{2}+d\ell ^{2}+(k^{2}+\ell ^{2})(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}),}

エリス排水孔の特殊なケースとしてエリスによって初めて提示されました (エリスワームホールを参照) 。

通過不可能なワームホールメトリックの 1 つのタイプは、シュワルツシルト解です(最初の図を参照)。

ds2＝−c2（1−2GMrc2）dt2+dr21−2GMrc2+r2（dθ2+罪2⁡θdφ2）。{\displaystyle ds^{2}=-c^{2}\left(1-{\frac {2GM}{rc^{2}}}\right)\,dt^{2}+{\frac {dr^{2}}{1-{\frac {2GM}{rc^{2}}}}}+r^{2}(d\theta ^{2}+\sin^{2}\theta \,d\varphi^{2}).}

オリジナルのアインシュタイン・ローゼン橋は1935年7月に発表された論文で説明されました。[ 65 ] [ 66 ]

シュワルツシルト球対称静的解の場合

ds2＝−11−2メートルrdr2−r2（dθ2+罪2⁡θdφ2）+（1−2メートルr）dt2、{\displaystyle ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}\right)\,dt^{2},}

適切な時間はどこですか？ ds{\displaystyle ds}c＝1{\displaystyle c=1}

を次のように置き換えるとr{\displaystyle r}あなた{\displaystyle u}あなた2＝r−2メートル{\displaystyle u^{2}=r-2m}

ds2＝−4（あなた2+2メートル）dあなた2−（あなた2+2メートル）2（dθ2+罪2⁡θdφ2）+あなた2あなた2+2メートルdt2{\displaystyle ds^{2}=-4(u^{2}+2m)\,du^{2}-(u^{2}+2m)^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+{\frac {u^{2}}{u^{2}+2m}}\,dt^{2}}

四次元空間は、数学的には、とに対応する二つの合同な部分、すなわち「シート」によって記述され、それらは超平面、あるいは が零となる平面によって結ばれる。このような二つのシート間の接続を「ブリッジ」と呼ぶ。あなた>0{\displaystyle u>0}あなた<0{\displaystyle u<0}r＝2メートル{\displaystyle r=2m}あなた＝0{\displaystyle u=0}グラム{\displaystyle g}

— A. アインシュタイン、N. ローゼン、「一般相対性理論における粒子問題」

アインシュタインとローゼンは、重力と電気の複合場に対して、次のようなシュワルツシルトの静的球対称解を導出した。

φ1＝φ2＝φ3＝0、φ4＝ε4、{\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0,\varphi _{4}={\frac {\varepsilon }{4}},}
ds2＝−1（1−2メートルr−ε22r2）dr2−r2（dθ2+罪2⁡θdφ2）+（1−2メートルr−ε22r2）dt2、{\displaystyle ds^{2}=-{\frac {1}{\left(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}}\right)}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}}\right)\,dt^{2},}

電荷は どこにありますか。ε{\displaystyle \varepsilon }

の場合の分母のない場の方程式は次のように書ける。 メートル＝0{\displaystyle m=0}

φμν＝φμ、ν−φν、μ{\displaystyle \varphi _{\mu \nu }=\varphi _{\mu ,\nu }-\varphi _{\nu ,\mu }}
グラム2φμν;σグラムνσ＝0{\displaystyle g^{2}\varphi _{\mu \nu ;\sigma }g^{\nu \sigma }=0}
グラム2（R私け+φ私αφけα−14グラム私けφαβφαβ）＝0{\displaystyle g^{2}(R_{ik}+\varphi _{i\alpha }\varphi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\varphi _{\alpha \beta }\varphi ^{\alpha \beta })=0}

特異点を解消するために、次の式に従って を に置き換えます。 r{\displaystyle r}あなた{\displaystyle u}

あなた2＝r2−ε22{\displaystyle u^{2}=r^{2}-{\frac {\varepsilon ^{2}}{2}}}

そして一つは[ 67 ] [ 68 ]メートル＝0{\displaystyle m=0}

φ1＝φ2＝φ3＝0{\displaystyle \varphi_{1}=\varphi_{2}=\varphi_{3}=0}そしてφ4＝ε（あなた2+ε22）1/2{\displaystyle \varphi _{4}={\frac {\varepsilon }{\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)^{1/2}}}}
ds2＝−dあなた2−（あなた2+ε22）（dθ2+罪2⁡θdφ2）+（2あなた22あなた2+ε2）dt2{\displaystyle ds^{2}=-du^{2}-\left(u^{2}+{\frac {\varepsilon^{2}}{2}}\right)(d\theta^{2}+\sin^{2}\theta \,d\varphi^{2})+\left({\frac {2u^{2}}{2u^{2}+\varepsilon^{2}}}\right)\,dt^{2}}

解は2枚のシートの空間内のすべての有限点に対して特異点を持たない。

— A. アインシュタイン、N. ローゼン、「一般相対性理論における粒子問題」

フィクションでは

ワームホールは、人間の一生スケール内で恒星間、銀河間、そして時には宇宙間移動を可能にするため、 SF作品ではよく見られる要素です。フィクションでは、ワームホールはタイムトラベルの手段としても使われてきました。

ワープポータルと高次元へのショートカット

理論物理学やSFにおいて、ワープまたはワープポータルの概念は、高次の空間次元にアクセスすることによってのみ可能となる空間の近道を説明する際に頻繁に用いられます。2次元空間において、離れた2点を近づけるためには、その平面を曲げたり折り畳んだりするための3次元の空間が必要となるのと同様に、 3次元空間において同様の操作を可能にするには、 4次元の空間軸内に埋め込まれている必要があります。[ 69 ]このアナロジーは、3次元空間を4次元の空間軸を通して曲げたり折り畳んだりすることで、離れた領域を隣接させることを可能にするワープポータルの描写の多くに見られます。

このようなメカニズムの存在は、たとえその次元が直接観測可能でなくても、宇宙が4次元の空間的枠組みを有している、あるいはその中に埋め込まれていることを意味する。これらの構造の幾何学は、ワームホール[ 70 ]やアルキュビエレ・ワープ・バブル[ 71 ]など、高次元の曲率に依存するアインシュタインの場の方程式の解を用いてモデル化されることが多い。

参照

注記

  1. ^記事内の画像の作成者が作成した、通過可能なワームホールの他のコンピューターレンダリング画像とアニメーションは、このページで見ることができます。このページには追加のレンダリングがあります。

参考文献

引用

  1. ^オーバーバイ、デニス(2022年10月10日). 「ブラックホールは私たちの宇宙に関する驚くべき秘密を隠しているかもしれない ― 重力と量子力学を加え、かき混ぜる。何が得られるだろうか？もしかしたら、ホログラフィック宇宙かもしれない」 .ニューヨーク・タイムズ. 2022年10月10日閲覧。
  2. ^ Choi, Charles Q. (2013年12月3日). 「不気味な物理現象が宇宙のワームホールを結びつける可能性」 NBCニュース. 2019年7月30日閲覧。
  3. ^ Cramer, John; Forward, Robert; Morris, Michael; Visser, Matt; Benford, Gregory; Landis, Geoffrey (1995). 「重力レンズとしての天然ワームホール」. Physical Review D. 51 ( 6): 3117– 3120. arXiv : astro-ph/9409051 . Bibcode : 1995PhRvD..51.3117C . doi : 10.1103/PhysRevD.51.3117 . PMID 10018782. S2CID 42837620 .  
  4. ^ 「『星への地下鉄』を探して」（プレスリリース）。 2012年4月15日時点のオリジナルよりアーカイブ。
  5. ^ソーン、キップ・S. (1994).ブラックホールとタイムワープ：アインシュタインのとんでもない遺産. ニューヨーク. p. 493. ISBN 978-0-393-31276-8。{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  6. ^ワイル、H. (1921)。「フェルドとマテリエ」。アンナレン・デア・フィジーク。65 (14): 541–563。Bibcode : 1921AnP...370..541W。土井：10.1002/andp.19213701405。
  7. ^エアハルト・ショルツ編。 (2001)。ヘルマン・ワイルの「Raum – Zeit – Materie および彼の科学的研究の一般的な紹介」。オーバーヴォルファッハセミナー。 Vol. 30. スプリンガー。 p. 199.ISBN​ 978-3-7643-6476-2。
  8. ^ a b「ヘルマン・ワイル」 ：スタンフォード哲学百科事典の項目。
  9. ^ Blum, Alexander S. (2022). 「ウッドチャックの穴からワームホールへ―ジョン・A・ウィーラーのノートブックを探る」 . Annalen der Physik . 534 (8) 2200244. Bibcode : 2022AnP...53400244B . doi : 10.1002/andp.202200244 . ISSN 1521-3889 . 
  10. ^ミスナー, チャールズ・W.; ソーン, キップ・S.; ズーレク, ヴォイチェフ・H. (2009-04-01). 「ジョン・ホイーラー、相対性理論、そして量子情報」 . Physics Today . 62 (4): 40– 46. Bibcode : 2009PhT....62d..40M . doi : 10.1063/1.3120895 . ISSN 0031-9228 . 
  11. ^ Novikov, Igor D.; Kardashev, NS; Shatskiy, AA (2010), Ciufolini, Ignazio; Matzner, Richard A. (eds.), "Wheeler Wormholes and the Modern Astrophysics" , General Relativity and John Archibald Wheeler , 367 , Dordrecht: Springer Netherlands: 39– 56, Bibcode : 2010ASSL..367...39N , doi : 10.1007/978-90-481-3735-0_4 , ISBN 978-90-481-3735-0、2025年2月20日取得{{citation}}: CS1 maint: work parameter with ISBN (link)
  12. ^ Misner, CW; Wheeler, JA (1957). 「古典物理学を幾何学として」. Ann. Phys . 2 (6): 525. Bibcode : 1957AnPhy...2..525M . doi : 10.1016/0003-4916(57)90049-0 .
  13. ^ a bヴィッサー、マット（1996年）『ロレンツワームホール』シュプリンガー・フェアラーク、ISBN 978-1-56396-653-8。
  14. ^ a bロドリゴ、エンリコ (2010)。スターゲイトの物理学。エリダヌス通信社。 p. 281.ISBN​ 978-0-9841500-0-7。
  15. ^ 「理論上は微小なワームホールが可能」phys.org . 2021年4月22日閲覧。
  16. ^ Blázquez-Salcedo, Jose Luis; Knoll, Christian; Radu, Eugen (2021年3月9日). 「アインシュタイン-ディラック-マクスウェル理論における通過可能なワームホール」 . Physical Review Letters . 126 (10) 101102. arXiv : 2010.07317 . Bibcode : 2021PhRvL.126j1102B . doi : 10.1103/PhysRevLett.126.101102 . hdl : 10773/32560 . PMID : 33784127. S2CID : 222378921. 2021年4月22日閲覧。  
  17. ^ Konoplya, RA; Zhidenko, A. (2022年3月4日). 「一般相対性理論における通過可能なワームホール」 . Physical Review Letters . 128 (9) 091104. arXiv : 2106.05034 . Bibcode : 2022PhRvL.128i1104K . doi : 10.1103/PhysRevLett.128.091104 . PMID 35302821. S2CID 247245028 .  
  18. ^ Schirber, Michael (2021年3月9日). 「Wormholes Open for Transport」 . Physics . 2021年4月22日閲覧。
  19. ^ Maldacena, Juan; Milekhin, Alexey (2021年3月9日). 「人間が通過可能なワームホール」 . Physical Review D. 103 ( 6) 066007. arXiv : 2008.06618 . Bibcode : 2021PhRvD.103f6007M . doi : 10.1103/PhysRevD.103.066007 .CC BY 4.0に基づいて利用可能です。
  20. ^ウラジミール・ドブレフ（編）、リー理論と物理学への応用：ブルガリア、ヴァルナ、2015年6月、シュプリンガー、2016年、246頁。
  21. ^ a b A. アインシュタインとN. ローゼン、「一般相対性理論における粒子問題」、物理学改訂48 (73) (1935)。
  22. ^ 「ブラックホールの説明 – 誕生から死まで」 YouTube 2018年8月12日。2021年12月11日時点のオリジナルよりアーカイブ。
  23. ^ 「ブラックホールへの崩壊」 Casa.colorado.edu. 2010年10月3日。2023年2月7日時点のオリジナルよりアーカイブ。 2010年11月11日閲覧。 この三次ソースは 他のソースからの情報を再利用しますが、そのソースの名前は示しません。
  24. ^フラム、L. (1916)。 「Beiträge zur Einsteinschen Gravitationstheorie」。物理的ツァイツシュリフト。17 : 448.（「アインシュタインの重力理論に関するコメント」）
  25. ^ Lindley, David (2005年3月25日). 「フォーカス：ワームホールの誕生」 .物理学. 15.アメリカ物理学会. 2016年2月20日閲覧。
  26. ^ Fuller, Robert W.; Wheeler, John A. (1962-10-15). 「Causality and Multiply Connected Space-Time」. Physical Review . 128 (2). American Physical Society (APS): 919– 929. Bibcode : 1962PhRv..128..919F . doi : 10.1103/physrev.128.919 . ISSN 0031-899X . 
  27. ^ Poplawski, Nikodem J. (2010). 「ねじれを伴う宇宙論：宇宙インフレーションの代替」. Phys. Lett. B. 694 ( 3): 181– 185. arXiv : 1007.0587 . Bibcode : 2010PhLB..694..181P . doi : 10.1016/j.physletb.2010.09.056 .
  28. ^ソーン、キップ・S. (1994).ブラックホールとタイムワープ：アインシュタインのとんでもない遺産. ニューヨーク. p. 488. ISBN 978-0-393-31276-8。{{cite book}}: CS1 maint: location missing publisher (link)
  29. ^ J. Wheeler (1957). 「量子幾何力学の性質について」. Ann. Phys . 2 (6): 604– 614. Bibcode : 1957AnPhy...2..604W . doi : 10.1016/0003-4916(57)90050-7 .(Misner と Wheeler (1957 年 12 月) のフォローアップ論文)
  30. ^エドゥアルド・プルゴベッキ、「量子幾何学：量子一般相対性理論の枠組み」、シュプリンガー、2013年、412ページ。
  31. ^ Ford; Roman (1995). 「平均エネルギー条件と量子不等式」. Physical Review D. 51 ( 8): 4277–4286 . arXiv : gr-qc/9410043 . Bibcode : 1995PhRvD..51.4277F . doi : 10.1103/PhysRevD.51.4277 . PMID 10018903. S2CID 7413835 .  
  32. ^ Sopova; Ford (2002). 「カシミール効果におけるエネルギー密度」. Physical Review D. 66 ( 4) 045026. arXiv : quant-ph/0204125 . Bibcode : 2002PhRvD..66d5026S . CiteSeerX 10.1.1.251.7471 . doi : 10.1103/PhysRevD.66.045026 . S2CID 10649139 .  
  33. ^ 「空間と時間の歪み」 Hawking.org.uk 。 2012年2月10日時点のオリジナルよりアーカイブ。2010年11月11日閲覧。
  34. ^ a b cモリス, マイケル; ソーン, キップ; ユルツェバー, ウルヴィ (1988). 「ワームホール、タイムマシン、そして弱エネルギー条件」(PDF) .フィジカル・レビュー・レターズ. 61 (13): 1446– 1449. Bibcode : 1988PhRvL..61.1446M . doi : 10.1103/PhysRevLett.61.1446 . PMID 10038800 . 
  35. ^ Olum (1998). 「超光速移動には負のエネルギーが必要」. Physical Review Letters . 81 (17): 3567– 3570. arXiv : gr-qc/9805003 . Bibcode : 1998PhRvL..81.3567O . doi : 10.1103/PhysRevLett.81.3567 . S2CID 14513456 . 
  36. ^ 「新発見のワームホールによりブラックホールから情報が脱出可能」 Quanta Magazine、2017年10月23日。
  37. ^ a b c dソーン、キップ・S. (1994).ブラックホールとタイムワープ. WWノートン. ISBN 978-0-393-31276-8。
  38. ^ Ian H., Redmount; Wai-Mo Suen (1994). 「ロレンツ時空泡の量子ダイナミクス」. Physical Review D. 49 ( 10): 5199– 5210. arXiv : gr-qc/9309017 . Bibcode : 1994PhRvD..49.5199R . doi : 10.1103/ PhysRevD.49.5199 . PMID 10016836. S2CID 39296197 .  
  39. ^ Kirillov, AA; P. Savelova, E. (2008). 「ワームホールガスからのダークマター」. Physics Letters B. 660 ( 3): 93– 99. arXiv : 0707.1081 . Bibcode : 2008PhLB..660...93K . doi : 10.1016/j.physletb.2007.12.034 . S2CID 12150385 . 
  40. ^ロドリゴ、エンリコ (2009). 「ワームホール-ブレーン遭遇の結末」. International Journal of Modern Physics D. 18 ( 12): 1809– 1819. arXiv : 0908.2651 . Bibcode : 2009IJMPD..18.1809R . doi : 10.1142/S0218271809015333 . S2CID 119239038 . 
  41. ^ a b John G. Cramer; Robert L. Forward; Michael S. Morris; Matt Visser; Gregory Benford & Geoffrey A. Landis (1995). 「重力レンズとしての天然ワームホール」 . Physical Review D. 51 ( 6): 3117– 3120. arXiv : astro-ph/9409051 . Bibcode : 1995PhRvD..51.3117C . doi : 10.1103/PhysRevD.51.3117 . PMID 10018782. S2CID 42837620 .  
  42. ^ HG Ellis (1973). 「排水孔を通るエーテルの流れ：一般相対論における粒子モデル」. J​​ournal of Mathematical Physics . 14 (1): 104– 118. Bibcode : 1973JMP....14..104E . doi : 10.1063/1.1666161 .
  43. ^ KA ブロンニコフ (1973)。 「スカラーテンソル理論とスカラー電荷」。アクタ フィジカ ポロニカ。B4：251～ 266。
  44. ^ Morris, Michael S. & Thorne, Kip S. (1988). 「時空におけるワームホールと星間旅行への利用：一般相対性理論の教育ツール」 . American Journal of Physics . 56 (5): 395– 412. Bibcode : 1988AmJPh..56..395M . doi : 10.1119/1.15620 .
  45. ^エリアス・グラバニス;スティーブン・ウィリソン (2007)。 」ガウス・ボネ重力における薄い殻からの「質量のない質量」。Phys . Rev. D . 75 (8) 084025. arXiv : gr-qc/0701152 . Bibcode : 2007PhRvD..75h4025G . doi : 10.1103/PhysRevD.75.084025 . S2CID  53529713 .
  46. ^ Fewster, Christopher J.; Ken D. Olum; Michael J. Pfenning (2007). 「境界を持つ時空における平均ヌルエネルギー条件」. Physical Review D. 75 ( 2) 025007. arXiv : gr-qc/0609007 . Bibcode : 2007PhRvD..75b5007F . doi : 10.1103/PhysRevD.75.025007 . S2CID 119726654 . 
  47. ^ Visser, Matt (1996). 「重力真空分極. II. Boulware真空におけるエネルギー条件」. Physical Review D. 54 ( 8): 5116– 5122. arXiv : gr-qc/9604008 . Bibcode : 1996PhRvD..54.5116V . doi : 10.1103 /PhysRevD.54.5116 . PMID 10021199. S2CID 31954680 .  
  48. ^グラハム、ノア；ケン・D・オラム（2007年）「非時平均ヌルエネルギー条件」Physical Review D. 76 ( 6) 064001. arXiv : 0705.3193 . Bibcode : 2007PhRvD..76f4001G . doi : 10.1103/PhysRevD.76.064001 . S2CID 119285639 . 
  49. ^アーバン、ダグラス；ケン・D・オラム（2010）「時空平均ヌルエネルギー条件」Physical Review D . 81 (6) 124004. arXiv : 1002.4689 . Bibcode : 2010PhRvD..81l4004U . doi : 10.1103/PhysRevD.81.124004 . S2CID 118312373 . 
  50. ^デュプレシス, フランシス; イーソン, ダミアン A. (2015). 「エキゾチカ・エクス・ニヒロ：二次重力の真空から探索可能なワームホールと非特異ブラックホール」. Physical Review D. 92 ( 4) 043516. arXiv : 1506.00988 . Bibcode : 2015PhRvD..92d3516D . doi : 10.1103/PhysRevD.92.043516 . S2CID 118307327 . 
  51. ^サスキンド、レナード (2005). 「ワームホールとタイムトラベル？あり得ない」. arXiv : gr-qc/0503097 .
  52. ^エヴェレット、アレン、ローマン、トーマス (2012). 『タイムトラベルとワープドライブ』 シカゴ大学出版局. p.  135. ISBN 978-0-226-22498-5。
  53. ^ Cramer, John G. (1994). 「NASA​​ Goes FTL Part 1: Wormhole Physics」 . Analog Science Fiction & Fact Magazine . 2006年6月27日時点のオリジナルよりアーカイブ。 2006年12月2日閲覧。
  54. ^ Visser, Matt ; Sayan Kar; Naresh Dadhich (2003). 「エネルギー条件の任意の小さな違反を伴う通過可能なワームホール」 . Physical Review Letters . 90 (20): 201102.1 – 201102.4 . arXiv : gr -qc/0301003 . Bibcode : 2003PhRvL..90t1102V . doi : 10.1103/PhysRevLett.90.201102 . PMID 12785880. S2CID 8813962 .  
  55. ^ Visser, Matt (1993). 「ワームホールからタイムマシンへ：ホーキングのクロノロジープロテクションに関するコメント」. Physical Review D. 47 ( 2): 554– 565. arXiv : hep-th/9202090 . Bibcode : 1993PhRvD..47..554V . doi : 10.1103/PhysRevD.47.554 . PMID 10015609. S2CID 16830951 .  
  56. ^ Visser, Matt (2002).年代学保護の量子物理学. arXiv : gr-qc/0204022 . Bibcode : 2003ftpc.book..161V .
  57. ^ Visser, Matt (1997). 「通過可能なワームホール：ローマリング」. Physical Review D. 55 ( 8): 5212– 5214. arXiv : gr-qc/9702043 . Bibcode : 1997PhRvD..55.5212V . doi : 10.1103/PhysRevD.55.5212 . S2CID 2869291 . 
  58. ^ Deutsch, David (1991). 「閉じた時間的直線近傍の量子力学」. Physical Review D. 44 ( 10): 3197–3217 . Bibcode : 1991PhRvD..44.3197D . doi : 10.1103/PhysRevD.44.3197 . PMID 10013776 . 
  59. ^ Brun; et al. (2009). 「局所的閉時間的曲線は量子状態を完全に区別できる」. Physical Review Letters . 102 (21) 210402. arXiv : 0811.1209 . Bibcode : 2009PhRvL.102u0402B . doi : 10.1103/ PhysRevLett.102.210402 . PMID 19519086. S2CID 35370109 .  
  60. ^ Pati; Chakrabarty; Agrawal (2011). 「閉じた時間的曲線を持つ混合状態の精製は不可能である」. Physical Review A. 84 ( 6) 062325. arXiv : 1003.4221 . Bibcode : 2011PhRvA..84f2325P . doi : 10.1103/PhysRevA.84.062325 . S2CID 119292717 . 
  61. ^ポルチンスキー、ジョセフ (1991). 「ワインバーグの非線形量子力学とアインシュタイン・ポドルスキー・ローゼンのパラドックス」.フィジカル・レビュー・レターズ. 66 (4): 397– 400.書誌コード: 1991PhRvL..66..397P . doi : 10.1103/PhysRevLett.66.397 . PMID 10043797 . 
  62. ^エンリコ・ロドリゴ、「スターゲイトの物理学：パラレル宇宙、タイムトラベル、ワームホール物理学の謎」、エリダヌス・プレス、2010年、281ページ。
  63. ^サミュエル・ウォーカー、「宇宙間旅行：ここから始めないだろう」、ニューサイエンティスト（2017年2月1日）。
  64. ^レイン、デレク、トーマス、エドウィン (2009).ブラックホール：入門（第2版）. インペリアル・カレッジ・プレス. p.  143. doi : 10.1142 /p637 . ISBN 978-1-84816-383-6。
  65. ^アインシュタイン、A.; ローゼン、N. (1935年7月1日). 「一般相対性理論における粒子問題」 .フィジカル・レビュー. 48 (1): 73– 77. Bibcode : 1935PhRv...48...73E . doi : 10.1103/PhysRev.48.73 .
  66. ^ 「Leonard Susskind | 「ER = EPR」または「ブラックホールの地平線の背後には何があるか?」2014年11月4日。2021年12月11日時点のオリジナルよりアーカイブ– www.youtube.comより。
  67. ^ 「宇宙の2つの領域を結ぶ磁気『ワームホール』が初めて発見」ScienceDaily .
  68. ^ 「磁気ワームホールが初めて生成」バルセロナUAB。
  69. ^ブライアン・グリーン（2004年）『宇宙の構造』クノップフ社、ISBN 978-0375727207。
  70. ^ Morris, Michael S.; Thorne, Kip S. (1988). 「時空におけるワームホールとその星間旅行への利用：一般相対性理論の教育ツール」 American Journal of Physics . 56 (5): 395–412. doi:10.1119/1.15620.
  71. ^アルクビエレ、ミゲル (1994). 「ワープドライブ：一般相対論における超高速移動」.古典重力と量子重力. 11 (5): L73–L77. doi:10.1088/0264-9381/11/5/001.

出典

ウィキメディア コモンズには、ワームホールに関連するメディアがあります。
「 https://en.wikipedia.org/w/index.php?title=Wormhole&oldid=1334504419#Interuniversal_travel」より取得