妖精のチェスの駒

カパブランカ チェスやその他の類似のチェスの変種で使用されるチャンセラー (左) とアーチビショップ (右) のチェスの駒のスタントンスタイルのデザイン。

妖精チェスの駒、変種チェスの駒、非正統的なチェスの駒、または異端のチェスの駒は、従来のチェスでは使用されないが、特定のチェスの変種や一部の非正統的なチェス問題に組み込まれているチェスの駒であり、妖精チェスとして知られています。従来の駒と比較すると、妖精の駒は主に動き方が異なりますが、捕獲、昇格などに関して特別なルールに従うこともあります。非正統的なチェスの発展は分散的で非協調的であるため、同じ駒が異なる名前を持つことがあり、さまざまな文脈で異なる駒が同じ名前を持つこともあります。

大半は図表上で標準的な駒を反転または回転させたアイコンとして表され、これらの「ワイルドカード」の意味はそれぞれの文脈において個別に定義される必要がある。問題ではなくチェスの変種で使用するために考案された駒には、専用のアイコンがデザインされている場合もあるが、一部の例外（プリンセス、エンプレス、そして時折アマゾン）を除き、これらの多くは、考案されたゲーム以外では使用されない。^{[ 1 ]}

背景

17世紀ロシアのチェス盤と駒の断片。これはかつて特定の地域におけるチェスの「標準」形式だった可能性がある。

チェスの最も古い形態は、7 世紀のペルシャ (チャトラン) とインド (チャトランガ) に遡ります。当時のルールは現代とは異なっていました。このゲームはアラブ人に伝わり、その後ヨーロッパ人に伝わり、数世紀に渡って古代のルールでプレイされました。たとえば、かつてクイーンは斜めに 1 マスしか動けませんでしたが、ビショップは斜めに 2 マスジャンプできました。ルールの変更は 15 世紀末にスペインで起こり、クイーンとビショップに現代的な動きが与えられました。古いイスラムの写本では、これら 2 つの駒はferz (顧問を意味する) とfil (象を意味する) と呼ばれていました。ロシア語とウクライナ語では、クイーンは今でもferz 、ビショップはslon (象)と呼ばれています。スペイン語ではビショップは今でも alfil ( al filから派生し、冠詞を使用) と呼ばれています。フェルズとアルフィルは、駒の動き方が変化するため、非標準的なチェスの駒とみなされています。15世紀に現代チェスを発明した人々と同様に、チェス愛好家は今でも独自のルールや駒の動き方を考案することがあります。標準ルールとは異なる動きをする駒は、「変種」または「妖精」と呼ばれる駒と呼ばれます。^{[ 2 ]}

妖精駒の名称は標準化されておらず、ほとんどは標準的なシンボルに関連付けられていません。図では、ほとんどの妖精駒は通常の駒のアイコンを回転させて表されますが、例外として、エクイホッパーとナイトの称号を持つ駒（プリンセス、エンプレス、アマゾン）^{[ 3 ]} 、そしていくつかの基本的なリーパー（ワジール、フェルズ、アルフィルなど）は独自のアイコンを持つ場合があります。^{[ 4 ]}ここでは可能な限り駒の一般的な名称を使用していますが、チェス問題に関連するサークルとチェスのバリアントに関連するサークルでは、これらの名称が異なる場合があります。

分類

最も単純な妖精チェスの駒の多くはオーソドックスなゲームには登場しませんが、通常は3つのクラスのいずれかに分類されます。^{[ 5 ]} 2つ以上の異なる駒の動きを組み合わせた複合駒もあります。

シンプルなピース

リーパーズ

跳躍者の名前と動き

メートル n	0	1	2	3	4
0	ゼロ( 0 )	ワジール（W）	ダババ（D）	スリーリーパー( H )	フォーリーパー
1	ワジール（W）	フェルズ( F )	ナイト（N）	ラクダ（C）	キリン
2	ダババ（ D）	ナイト（N）	アルフィル（A）	シマウマ（Z）	雄鹿
3	スリーリーパー( H )	ラクダ（C）	シマウマ（Z）	トリッパー（G）	アンテロープ
4	フォーリーパー	キリン	雄鹿	アンテロープ	通勤者
ピースの名称は異なる場合があります。この表では、各ピースの最も一般的な名称を使用しています。

跳躍駒とは、一定距離離れたマス目に直接移動する駒です。跳躍駒は、敵の駒があるマス目を占領することで駒を取ります。跳躍駒の動きはブロックできません（シャンチーやジャンギにおける象や馬とは異なります）。跳躍駒は、間に挟まれた駒を「飛び越える」ため、跳躍駒のチェックを妨害することはできません。跳躍駒はピンを作ることはできませんが、効果的な分岐駒です。跳躍駒の動きが直交（水平または垂直）でも斜めでもないものは、ヒッポゴナル（水平または垂直）と呼ばれます。

リーパーの動きは、着地マスまでの距離、つまり一方向に直交するマスの数と直角方向に直交するマスの数で表すことができます。例えば、オーソドックスなナイトは(1,2)リーパーまたは(2,1)リーパーと呼ばれます。^{[ 6 ]}右の表は、4マスまでのリーパーの一般的な（ただし決して標準的なものではない）名称と、妖精駒の表記法としてよく使われるベッツァ表記法における文字を示しています。

隣接するマスへの移動は、通常の用法では厳密には「跳躍」とはみなされませんが、一般性のためにここに含めています。隣接するマスへの移動のみを行う跳躍手は、将棋の変種においてはステップムーバーと呼ばれることがあります。^{[ 7 ]}

チェスのペルシア語源であるシャトランジでは、ビショップとクイーンの前身はリーパーでした。アルフィルは(2,2)-リーパー（任意の方向に2マス斜めに移動する）、フェルズは(1,1)-リーパー（任意の方向に1マス斜めに移動する）です。^{[ 8 ]}ワジールは(0,1)-リーパー（「直交」1マスリーパー）です。ダババは(0,2)-リーパーです。レベル3のリーパーは、スリーリーパー（0,3）、ラクダ（1,3）、シマウマ（2,3）、トリッパー（3,3）です。レベル4のリーパーは、フォーリーパー（0,4） 、キリン（1,4）、スタッグ（2,4）、アンテロープ（3,4）、コミューター（4,4）です。これらの基本的なリーパーの多くはティムールのチェスに登場します。

Ferz（表記F）

アルフィル（表記A）はジャンプできる。

ワジール（表記W）

ダババ（表記D）はジャンプできます。

ライダー

ライダー、またはレンジングピースは、他の駒がない限り、一方向に無制限の距離を移動できる駒です。各基本ライダーは基本リーパーに対応しており、障害物に到達するまで、そのリーパーの動きを一方向に繰り返すと考えることができます。障害物が味方の駒であれば、それ以上の移動は阻止されます。障害物が敵の駒であれば、捕獲することはできますが、飛び越えることはできません。

オーソドックスチェスには3種類のライダーがあります。ルークは(0,1)ライダー、ビショップは(1,1)ライダー、クイーンは両方のパターンを組み合わせたものです。スライダーはライダーの特殊なケースで、幾何学的に連続したセル間でのみ移動できます。オーソドックスチェスにおけるライダーはすべてスライダーの例です。

	1つの	b	c	d	e	f	グラム	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	1つの	b	c	d	e	f	グラム	h

ナイトライダー(反転したナイトで表現) は、任意の数のナイトを同じ方向に動かします。

	1つの	b	c	d	e	f	グラム	h
8									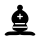8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	1つの	b	c	d	e	f	グラム	h

a1の白のナイトライダーは、b3のポーンによってc5への到達を阻まれている。a2、b2、b1の駒とは独立してc2へ移動できる。e3の敵ポーンを捕獲することはできるが、g4へは移動できないため、黒のキングはチェックされていない。黒のeポーンはピン留めされている。これは、移動することでキングがチェックにさらされるからだ。白のクイーンとルークは、a8の黒のナイトライダーによって串刺しにされている。したがって、NNxe3+が可能である。

ライダーはピンと串刺しの両方を作ることができます。人気の高いフェアリーチェスのライダーの 1 つにナイトライダーがあります。ナイトライダーは、どの方向にも無制限にナイトを動かすことができます (他のライダーと同様に、動きの途中で方向を変えることはできません)。ライダーの名前は、多くの場合、基本となるリーパーの名前に接尾辞「ライダー」を追加したものです。たとえば、ゼブラライダーは (2,3) ライダーです。ナイトライダーは、その構成要素であるナイトの動きの 1 つが落ちるマス目でのみブロックされます。つまり、ナイトライダーが a1 から開始する場合、b3 または c2 でブロックできますが、a2、b2、または b1 ではブロックできません。ナイトライダーは、介在するマス b3 が空いている場合のみ、a1 から c5 に移動できます。

一般的なライダーの中には、直線的な軌道を辿らないものもあります。グラント・アセドレックスという歴史的なゲームに登場するアアンカは、まさに「曲がったライダー」です。最初の一歩はフェルズのように踏み出し、そこからルークのように外側へ進みます。同じゲームに登場するユニコーンは、最初の一歩はナイトのように踏み出し、そこからビショップのように外側へ進みます。非常に大きなチェス盤で使用されるローズは、ほぼ正八角形上でナイトの動きの軌道を描きます。e1からg2、h4、g6、e7、c6、b4、c2へと進み、e1に戻ります。曲がったビショップ、つまりボーイスカウトはジグザグに進み、f1からe2、f3、e4、f5、e6、f7、e8（またはg2、f3、g4、f5、g6、f7、g8）へと進みます。

射程が制限された駒は、ライダーのように動きますが、特定の数までしか移動できません。例えば、チェスの異なる軍隊を持つショートルークは、ルークのように動きますが、移動距離は4マスまでです。a1からb1、c1、d1、e1までは1回の移動で移動できますが、f1までは移動できません。ライダーに対応するリーパーは、射程が1の射程が制限された駒と考えることができます。ワジールは、一度に1マスしか移動できないルークです。大将棋（日本の古代将棋）の荒牛と飛龍は、それぞれ射程2のルークと射程2のビショップです。

他にも一般化できる例がある。ティムールチェスのピケットはビショップのように動くが、少なくとも2マス移動する（したがって、隣のマスに止まることはできないが、そこでブロックすることはできる）。これらは一般にスキー駒と呼ばれる。ピケットはスキービショップである。スキップライダーは最初のマスを飛び越え、次に進路上のすべての奇数マスを飛び越える。スキップしたマスでブロックされることはない。したがって、スキップルークはダババリダー、スキップビショップはアルフィルライダーとなる。スリップライダーも同様だが、 2番目のマスを飛び越え、次に進路上のすべての偶数マスを飛び越える。 ^{[ 9 ]}

将棋の変種（チェスの変種）の中には、面移動と呼ばれる駒もあります。これは、一定の回数まで同じ基本手順を繰り返し、駒を捕獲したら必ず停止するという点で、限定射程駒に似ています。しかし、他の騎手とは異なり、騎手は移動中に方向を変えることができ、騎手やベント騎手のように決まった軌道を持ちません。

ホッパー

大砲（砲）の遠距離の脅威：示されている動きは砲の動きです（ここでは「俥」を占領しています）。

ホッパーとは、他の駒（ハードルと呼ばれる）を飛び越えて移動する駒です。ハードルは、任意の色の駒であれば何でも構いません。他の駒を飛び越えることができなければ、ホッパーは移動できません。ホッパーは通常、ハードルを飛び越えるのではなく、移動先のマスにある駒を取ることで捕獲します（チェッカーの場合）。例外として、イナゴは犠牲者を飛び越えて捕獲する駒です。イナゴはホッパーの一種と見なされることがあります。

西洋のチェスにはホッパーは存在しません。シャンチー（中国のチェス）では、大砲はルークのラインに沿ってホッパーとして捕獲します（捕獲していないときは、ジャンプできない（0,1）ライダーで、ルークと同じです）。ジャンギ（韓国のチェス）では、大砲は移動中または捕獲中にルークのラインに沿ってホッパーですが、味方であれ敵であれ、他の大砲をジャンプすることはできません。バッタはクイーンと同じラインに沿って移動し、他の駒を飛び越えてそのすぐ先のマスに着地します。ヤンチーには、大砲の対角線上の駒であるヴァオが含まれており、これはビショップとして移動し、ビショップのラインに沿ってホッパーとして捕獲します。

複合ピース

複合駒は、2つ以上の駒の力を組み合わせたものです。クイーンはルークとビショップを組み合わせたものと考えることができます。標準チェスのキングは、フェルズとワジールを組み合わせたもので、チェックとチェックメイトの制限とキャスリングを無視します。アリババはダババとアルフィルを組み合わせたもので、リスは2ユニット離れた任意のマスに移動できます（ナイトとアリババを組み合わせたもの）。フェニックスはワジールとアルフィルを組み合わせたもので、キリンはフェルズとダババを組み合わせたものです。これらはどちらも、今日でも時々プレイされる古い日本のチェスの変種である 中将棋に登場します。

両生類は、その構成要素のいずれよりも広い範囲を跳躍する複合跳躍者です。例えば、カエル​​は(1,1)-(0,3)跳躍者です。(1,1)跳躍者は盤面の半分、(0,3)跳躍者は盤面の9分の1に制限されていますが、これらの組み合わせは盤面のどのマスにも到達できます。^{[ 10 ]}

組み合わせた駒の 1 つがナイトの場合、その複合駒はナイト駒と呼ばれることがあります。アーチビショップ、チャンセラー、アマゾンの3 つは、非ロイヤルのオーソドックスなチェスの駒の力を組み合わせた人気の複合駒です。これらはそれぞれ、ナイトビショップ、ナイトルーク、ナイトクイーンです。組み合わせた駒の 1 つがキングの場合、その複合駒はクラウンピースと呼ばれることがあります。クラウンナイトは、ナイトとキングの動き (ロイヤルの場合は、ナイトキングと呼ばれます) を組み合わせたものです。将棋の竜王はクラウンルーク (ルーク + キング) であり、竜馬はクラウンビショップ (ビショップ + キング) です。ナイト複合駒は、複合駒が上記の 3 つの基本カテゴリのいずれにも当てはまらないことを示しています。プリンセスはビショップの動きではスライドしますが (その方向の障害物によってブロックされる可能性があります)、ナイトの動きではリープします (その方向ではブロックされません)。 （プリンセスと皇后という名前は、プロブレム主義の伝統では一般的です。これらの駒を使ったチェスのバリアントでは、カパブランカチェスではそれぞれ大司教と長官、グランドチェスでは枢機卿と元帥など、別の名前で呼ばれることがよくあります。）ファルコンチェスのハヤブサと既知の駒の組み合わせは、翼のある駒と呼ばれます。完全順列チェスでは、翼のあるナイト、ビショップ、ルーク、クイーンだけでなく、翼のある元帥、翼のある枢機卿、翼のあるアマゾンも登場します。^{[ 11 ]}

海の駒は、ライダーまたはリーパー（通常の動き）とイナゴ（捕獲）が同じ方向に並んだ複合駒です。海の駒には、海やその神話にちなんだ名前が付けられています。例えば、ネレイド（海の司教）、トリトン（海のルーク）、マーメイド（海の女王）、ポセイドン（海の王）などです。神話に登場しない海の生物にちなんで名付けられた例としては、タツノオトシゴ（海の騎士）、イルカ（海のナイトライダー）、アネモネ（海の護衛またはマン）、エビ（海のポーン）などがあります。これらの海の駒を使ったゲームは「シーチェス」と呼ばれ、イナゴのような捕獲の動きにより多くのマスが必要となるため、より大きな盤上でプレイされることが多いです。

制限作品

駒の力を組み合わせるだけでなく、特定の方法で制限を加えることで、駒を改変することもできます。例えば、駒の力を移動のみ、捕獲のみ、前進のみ、後退のみ、横移動のみ、最初の移動のみ、特定のマス目のみ、特定の駒に対してのみ、などです。象棋（中国将棋）の馬は跳躍できないナイトです。馬は、隣接するマス目ではブロックされます。大将棋の石将は前進のみ可能なフェルズです（そのため、盤の端に到達するとブロックされます）。

このような制約は、組み合わせることもできる。将棋の金将はワジールと前進のみのフェルズを組み合わせたもので、将棋の銀将はフェルズと前進のみのワジールを組み合わせたものである。ポーンはワジールの力を持つが、前進と移動のみに限られ、フェルズの力を持つが、前進と捕獲のみに限られ、2マスの範囲に限定されたルークの力を持つが、前進のみで捕獲はできず、最初の移動のみに限られ、より強力な駒に置き換えられる力を持つが、最後の段に到達した時のみに限られ、そしてアンパッサンで捕獲する力を持つ。ポーンのように動き方や捕獲の仕方が異なる駒は分岐駒と呼ばれる。^{[ 12 ]}

以下に説明するように、基本的な楽曲の基本的な制約の任意の組み合わせをより簡潔に表現できる強力な表記法がいくつかあります。

キャプチャ

上記の駒はすべて、アンパサント（アンパサント）を除き、1ターンに1回移動し、交換（つまり、犠牲者のマスに移動して交換する）によって捕獲します。射撃駒（ライフルチェスなど）は交換による捕獲は行いません（捕獲時にその場に留まります）。このような射撃による捕獲は、古くからよく行われていた日本のチェスでは「居喰い」と呼ばれています。バロックチェスには、隣接する駒から直接離れて捕獲する「撤退駒」など、交換による捕獲を行わない駒の例が多くあります。

1ターンに複数回移動する

中将棋の獅子は、マルセイユチェスの駒と同様に、 1ターンに2回動くことができます。このような駒は、将棋の変種と呼ばれる日本の古いチェスの変種でよく見られ、最も単純な例にちなんで「獅子手」と呼ばれています。獅子は1ターンに2回動く力を持つ王様です。つまり、獅子は駒を捕獲してから移動し、さらに別の駒を捕獲したり、元のマスに戻ったりすることができます。2回動く駒が駒を捕獲してから元のマスに戻る場合、それは「射駒」のように機能します。

ゲーム

赤/黒の象（アルフィルス）

赤/黒の大砲

Xiangqiゲームピースディスク

桂馬（けいま）

ヒシャ（ルーク）

将棋の駒

いくつかの種類の駒は特定のゲームに由来し、共通の特徴を持っています。例えば、チェスに似た中国のゲームであるシャンチーの駒が挙げられます。最も一般的な駒は、レオ、パオ、ヴァオ（中国の大砲に由来）、そしてマオ（馬に由来）です。大砲に由来する駒は、捕獲時はホッパーのように動き、それ以外はライダーのように動くことで区別されます。

シャンチーの駒は通常、円盤状で、駒を識別するための漢字がラベルまたは刻印されています。将棋の駒は通常、くさび形のチップ状で、駒を識別するための漢字が刻印されています。

特別な属性

妖精駒は動き方が様々ですが、中には特別な特性や能力を持つものもあります。ジョーカーは（その定義の一つにおいて）対戦相手の最後の動きを模倣します。例えば、白がビショップを動かすと、黒はジョーカーをビショップとして動かすことができます。孤児駒には独自の移動力はありませんが、攻撃してきた敵駒と同じように動きます。つまり、ルークが孤児駒を攻撃すると、孤児駒はルークと同じ移動力を持つようになりますが、敵のルークが離れるとその力は失われます。孤児駒はこれらの伝達された力を使って互いに攻撃し合い、連鎖を形成します。^{[ 13 ] [ 14 ]}

ロイヤル駒は、決して捕獲されてはならない駒です。ロイヤル駒が捕獲の脅威にさらされ、次の手で捕獲を避けられない場合、ゲームは負けとなります (チェックメイトの一般化)。オーソドックスなチェスでは、キングがロイヤルです。フェアリーチェスでは、他のどの駒でもロイヤルになることができ、複数であっても、まったくロイヤルにならないこともあります (この場合、勝利条件は、相手の駒をすべて捕獲するか、ポーンを昇格させるなど、他の目標である必要があります)。ティムールチェスと中将棋では、昇格によって複数のロイヤルを作成できます。ロイヤル駒が複数ある場合、ゲームは、そのうちの 1 つを捕獲するか (絶対ロイヤル)、すべてを捕獲すると (絶滅ロイヤル)、勝利できます。ルールでは、チェックしたままにできるロイヤルの数に制限を設けることもできます。スパルタチェスでは、黒にキングが 2 体あり、1 回のターンで両方を捕獲することはできませんが、両方をチェックしたままにすることはできません。レックス・マルチプレックスというフェアリーチェスの条件では、ポーンはキングに昇格することができる。複数のキングを同時にチェックする動きは、次の動きですべてのチェックが解決されない限り、違法である。チェックメイトは、ある動きで反対色のすべてのキングがチェックメイトされると発生する。（プレイヤーは、たとえ他の攻撃されたキングのチェックやチェックメイトを解決するためであっても、自分のキングをチェックやチェックメイトにさらしてはならない。）^{[ 15 ]}

駒は、動くと、自分自身または他の駒に (一時的または永続的な) 効果を生み出すことができます。ナイトリレーチェスでは、ナイトは守っている味方の駒に、ナイトのように動く能力を与えます。この能力は一時的なもので、駒がナイトに守られなくなると無効になります。アンダーナッハチェスでは、動いたり捕獲したりする駒の色が変わります。フェアリーチェスの問題の一種であるボラージュでは、駒は明るいマス目から暗いマス目 (その逆) に初めて動いたときに色が変わり、その後は色が固定されます。マドラスチェスでは、同じ種類だが色が異なる 2 つの駒が互いを攻撃すると、一時的に互いが麻痺します。つまり、外側の駒によって相互の攻撃が阻止されるまで、どちらも動けなくなります。ラルフ・ベッツァの『ネモロス』に登場するバジリスクは、この麻痺を永続的に付与します（ただし、麻痺した駒はゲーム内の別の駒である「ゴーアウェイ」によって押される可能性があり、自発的に動くことしかできなくなります）。同ゲームに登場するガストは、2マス以内の味方駒の動きを、自身から幾何学的に遠ざかる方向に制限し、敵駒にも同様に移動を強制します（オーソドックスチェスにおける王手解決の強制に似ています）。バロックチェスのイモビライザーは、隣接する駒の動きを制限します。天竺将棋の火鬼と古将棋の毒炎は、ターン終了時に自身と隣り合った敵駒を捕獲します。マカ大大将棋のティーチングキングとブッダスピリットは「伝染性」があり、ティーチングキングまたはブッダスピリットを捕獲した駒は、ティーチングキングまたはブッダスピリットになります（これは一種の強制昇格と見なすことができます）。

駒は、オーソドックスなチェスのポーンのように、他の駒に昇格することがあります。ポーンは昇格先を選択できます。シャンチーでは、ポーンは盤の中央の川を渡るとすぐに自動的に昇格しますが、この昇格は固定されており、前方だけでなく横方向にも移動する力しか与えられません。将棋では、ポーンだけが昇格できる駒ではありません。昇格は、プレイヤーの観点から最後の3つの列で部分的または全体的に移動が行われた場合にも発生する可能性があり、駒がそれ以上動けなくなった場合を除き任意ですが、駒の昇格は固定されています。大大将棋では、昇格できる駒が捕獲を行った場合に昇格（これも駒によって固定）が起こり、拒否することはできません。

駒の移動場所に制限がある場合もあります。シャンチーでは、将軍と顧問は宮殿（各プレイヤーの盤上の3×3の区画）から出られません。盤のトポロジーも変更可能で、一部の駒はそれを尊重しますが、他の駒はそれを無視します。ティムールチェスでは、王、王子、または先住王のみが相手の城塞に入ることができ、先住王のみが自身の城塞に入ることができます。円筒チェスでは、左右の端が互いにつながっているため、ルークはh1から右に進み、最終的にa1に到達できます。円筒形の駒と通常の駒の両方を同じ盤上に置くことも可能です。

駒には捕獲方法に制限がある場合もあります。鉄の駒は全く捕獲できないかもしれません。^{[ 16 ]}他にも、将棋でよくあるように、一部の駒には捕獲できるが他の駒には捕獲できない駒など、様々な可能性があります（例えば、盾のユニットは弓や銃に対して無敵です）。ラルフ・ベッツァのジュピター軍では、木星のビショップはネメシスフェルズです。つまり、捕獲できず、敵のキングとの距離を広げることもできず、捕獲されることもありません（ただし、敵のキング自身に捕獲されることはありますが、ベッツァはこの点について優柔不断です）。^{[ 17 ]}

このような駒の特殊な特徴は、通常、妖精駒の動きを記述する記法には含まれておらず、別途説明されることが多い。

高次元

ラウムシャッハなどの3 次元チェスのバリエーションもいくつか存在し、盤上の追加の次元を利用する駒も存在します。

E D C B あ ラウムシャッハでは、ユニコーンは立方体の頂点（つまり、空間の対角線に沿って）を移動します。Cd4のユニコーンは、黒点のあるマスに移動できます。ボードは重ねられており、ボードEが一番上にあります。

チェスの亜種や妖精の駒の動きは、3次元以上のものも存在する。例えば、チェスの亜種ビデオゲーム「5D Chess with Multiverse Time Travel」では、4次元の動きが利用可能である。このゲームに登場する妖精の駒の1つはドラゴンと呼ばれ、移動時には4次元すべてを使用する。特に、移動経路の途中で移動を妨げる駒がない限り、4次元に沿って任意の距離、各次元に沿って等しい距離を移動することができる。このゲームでは、このような経路を形成する正方形の直線を四角形と呼ぶ。^{[ 18 ]}

表記

パーレットの移動記法

デイヴィッド・パーレットは著書『オックスフォード・ボードゲームの歴史』^{[ 19 ]} の中で、妖精の駒の動きを記述するための記法を用いています。動きはm={式}という形式で指定されます。ここでmは「動き」を意味し、式は以下の要素から構成されます。

• 距離（数値、n）
  • 1 – 距離1（つまり隣接するマスまで）
  • 2 – 2の距離
  • n – 指定された方向の任意の距離
• 方向（句読点、X）
  • + – 直交方向（4つの方向が可能）
  • > – 直交前方
  • < – 直交後方
  • <> – 直交前方および後方
  • = – 直交横方向（ここではパーレットの除算記号÷の代わりに使用）
  • >= – 前方または横方向に直角
  • <= – 直交後方または横方向
  • X – 斜め（4つの方向が可能）
  • X> – 斜め前
  • X< – 斜め後ろ
  • ✳ – 直交または斜め（全8方向）; +Xと同じ; Parlettは*を使用する
• グループ化
  • / –スラッシュで区切られた2つの直交移動は、ヒッポゴナル移動（つまり、ナイトのようなジャンプ）を表します。
  • & – 同じ方向への繰り返しの動き、例えば、ヒッポゴナルライダー（例：ナイトライダー）
  • . – それから、（例えば、アアンカは1X.n+です。斜めに1歩進み、それから直交方向に任意の距離進みます）

パーレットへの追加

Parlett をさらに完全なものにするために、次のものを追加できます。

• 移動が発生する可能性のある条件（nを除く小文字の英数字）
  • （デフォルト） – ゲームのどの時点でも発生する可能性があります
  • i – 最初の動き（例：ポーンの2手目）でのみ実行できます
  • c – 捕獲時にのみ実行できます（例：ポーンの斜め捕獲）
  • o – 捕獲には使用できません（例：ポーンの前進）
• 移動タイプ
  • （デフォルト） – ピースの上に着地することで捕獲する。中間のピースによってブロックされる。
  • ~ – リーパー（跳躍）; 相手の駒に着地して捕獲する
  • ^ – イナゴ（跳躍して捕獲する；ホッパーを意味する）；捕獲した駒の1マス先への移動
• グループ化（句読点）
  • , (カンマ) – 移動オプションを区切ります。カンマで区切られたオプションは、移動ごとに1つだけ選択できます。
  • () – グループ化演算子。ナイトライダーを参照
  • - – 範囲演算子

形式（グループ化を除く）は次のとおりです: <条件> <移動タイプ> <距離> <方向> <その他>

これを基に、伝統的なチェスの動き（キャスリングとアンパッサンキャプチャを除く）は次のようになります。

• キング：1✳
• 女王: n ✳
• ビショップ: nX
• ルーク: n+
• ポーン: o1>, c1X>, oi2>
• ナイト: ~1/2

ラルフ・ベッツァの「面白い記法」

ラルフ・ベッツァは、基本的な駒の動きと修飾子に基づいて、妖精チェスの駒（標準的なチェスの駒を含む）の分類体系を作成した。^{[ 20 ]}

大文字は、1マスの直交移動から3×3の斜め移動まで、基本的な跳躍動作を表します。Wazir 、 Ferz 、 D abbaba、K Night、A lfil、T H reeleaper (ort H ogonal)、C amel、Z ebra、dia G onal (3,3)-leaper などです。CとZは、現在はあまり使われていない旧式の文字L (Long Knight) とJ (Jump)に相当します。より長い跳躍は、キリンの場合は (1,4) のようにベクトルで指定します。

ベッツァの駒の動きの「原子的」記法

原子	名前	ボードステップ
W	ワジール	（1,0）
F	フェルズ	（1,1）
D	ダババ	（2,0）
北	騎士	（2,1）
あ	アルフィル	（2,2）
H	スリーリーパー	（3,0）
C (旧L )	キャメル	（3,1）
Z（旧J）	シマウマ	（3,2）
G	トリッパー	（3,3）

リーパーは、その文字を2つ重ねることでライダーに変換されます。例えば、WWはルーク、FFはビショップ、NNはナイトライダーを表します。2つ目の文字は数字にすることができ、これはリープ動作を何回繰り返すことができるかの制限を表します。例えば、W4はルークの移動が4マスに制限されていることを示します。R4はW4の古い同義語です。^{[ 21 ]}

複数の移動文字を文字列に組み合わせると、駒は利用可能な選択肢のいずれかを使用できることを意味します。例えば、WFはキングを表し、キングは直交または斜めに1マス移動できます。

ポーン（特に複雑）とナイト（基本的な跳躍動作）を除く標準的なチェスの駒には、独自の文字が用意されています。K = WF、Q = WWFF、B = FF、R = WWです。^{[ 21 ]}

言及されているすべての大文字は、移動とキャプチャの両方に使用できる最大限対称な一連の動きを指します。大文字の前の小文字はコンポーネントを修飾し、通常は動きをサブセットに制限します。これらは、方向修飾子、モーダル修飾子、およびその他の修飾子で区別できます。基本的な方向修飾子は、forward、backward、right、leftです。非直交の動きの場合、これらは動きのペアを示し、単一の方向を完全に指定するには、percentageタイプの2番目の修飾子が必要です。そうでない場合、複数の方向について言及されているときは、これらすべての方向への動きが可能であることを意味します。接頭辞表記s sideways およびverticalは、それぞれlrおよびfbの省略形です。モーダル修飾子は、 moveのみ、captureのみです。その他の修飾子は、jumping（基本的な遠距離跳躍、ジャンプしなければならず、障害なしでは移動できない）、n中国象のようなon-jumping、g rasshopper（最初に遭遇したピースのすぐ先のマス目に着地することによってのみ移動するライダー）、p ao（最初に遭遇したピースの任意の数のマス目に着地することによってのみ移動するライダーだが、2 番目のピースを超えることはできない）、o cylinderly（ボードの片側から移動すると、反対側に巻き付く）、 z crooked（ボーイスカウトのようにジグザグに移動）、 q circular movement（バラのように）、およびthen（グリフォンのように、一方向に動き始めてから別の方向に動き続けるピース）です。

さらに、ベツァは表記に括弧を追加することも提案しています。q[WF]q[FW] は循環的なキングとなり、e4 から f5 (最初に ferz の動き) に動き、次に g5、h4、h3、g2、f2、e3 と動き、e4 に戻って効果的にターンをパスします。また、e4 から f4 (最初に wazir の動き) に動き、次に g5、g6、f7、e7、d6、d5 と動き、e4 に戻ることもできます。

例: 標準的なチェスのポーンは、mfWcfF (最初の 2 度の移動を無視) と記述できます。

構成要素と修飾語の順序は決まっていません。ベッツァは、発音しやすい曲名や芸術的な言葉遊びを作るために、順序を巧みに操ることがよくあります。

ベッツァの基本的な跳躍の記法

X はい	−3	−2	−1	0	1	2	3
3	G	Z	C	H	C	Z	G
2	Z	あ	北	D	北	あ	Z
1	C	北	F	W	F	北	C
0	H	D	W	0	W	D	H
−1	C	北	F	W	F	北	C
−2	Z	あ	北	D	北	あ	Z
−3	G	Z	C	H	C	Z	G

この表はデカルト座標平面の特殊なケースであり、原点は常に移動しようとしている駒の 現在の位置であることに注意してください。

ベッツァ記法への追加（「XBetza」）

ベッツァは小文字のi は用いない。これはここでは、ポーンの種類を表す頭文字として用いられている。文字aはここでagainを表すために用いられており、駒が前置された動きを複数回実行できることを示している。a の後ろには新たな修飾語句が付記される可能性があり、その修飾語句は動きの2番目の「レグ」に適用される。このような継続ステップの方向指定は、最初のステップを基準として解釈されるべきである（例えば、aW は方向を変更できる2ステップの直交移動であり、afW は同じ方向を継続しなければならない2ステップの直交移動である）。^{[ 22 ]}

頻繁に発生する特殊な動きを処理するために、e をmおよびcの次に使用して、アンパッサントキャプチャー、つまりiおよびn修飾子を使用して移動したばかりの駒を、 nが示すブロックできた可能性のあるマスに移動することによってキャプチャーすることを示します。(これで、FIDE ポーン mfWcefFimfnD の完全な説明が作成されます。)範囲指定子付きのOは、初期セットアップでその方向に最も遠い駒でキャスリングすることを示すために使用されます。範囲は、キングが移動するマスの数を示します (オーソドックス キャスリング: ismO2)。XBetza は、元の意味が意味をなさない場合に別の意味を与えることで、一部の修飾子をオーバーロードします。たとえば、継続レグ ('iso') 内のi は、長さが前のライディング レグと同じでなければならないことを示し、ライフル キャプチャー (caibR) を示すのに役立ちます。

複数レグの移動の最終でないレグでは、占有されているマス目でその内容を乱さずに終了するオプションもあります。これを示すために修飾子pが使用され、最終レグの場合とは少し意味が異なります。この場合、従来の意味はpafの省略形と見なすことができます。 a表記をより汎用的にするために、2 つのレグの移動が正確に一致しない場合にも使用できます。gは、占有されているマス目への最終でないレグを示す代替ですが、pとは対照的に「範囲トグル」を指定し、言及されているライダー移動を次のレグの対応するリーパー移動 (例: R ⟷ W ) に変換し、その逆も同様です (従来のgはgafの省略形になります)。空のマス目に到達したときの同様の範囲トグルはyで示すことができ、スライダーがリープで開始した後に自発的にコーナーを曲がることを示します。最初のレグが 4 倍対称性しか持っていなかったとしても、継続方向は常に 8 倍 ( K ) システムにエンコードされます。 4 重対称の移動における中間方向の指定は、直交移動を対応する斜め移動に交換します (例: W ⟷ F )。また、その逆も同様です。 (つまり、 mafsW はシャンチー馬で、空の W マスに移動し、45 度で 1 つの F ステップを継続します。 FyafsF はグリフォンです。)

Bex 表記法では、さまざまな捕獲モードを示すための拡張機能も多数追加されています。チェスのように単純なcで置換捕獲を表し、 [ca]、[cw]、[cl]などの表記法は接近、撤退、飛び越えなどによる捕獲を表します。[crM]はライフル捕獲(つまり、移動せずに敵の駒を全滅させること)を表し、アトムMを使用して、その方法で捕獲できるものを指定します。Bex 表記法では、より長い移動のステップとしてエキゾチックな効果を記述する方法も導入されています。たとえば、最終移動ステップの[xo]は元のマスに戻ることを示し、[xiK]は現在のマスからKステップ離れたすべての駒を動けなくすることを意味しますが、 [x!iK]は同様にそのような隣接する駒を動かします。[xwN]はNステップ離れた駒との位置の交換を示します。これらのことはどれも元の Betza 表記法では指定できませんが、表記法が完全にアドホックであり、基本原理に従っていないという欠点があります。

問題論者が使用する表記法

英国チェス問題協会（BCPS）は、多くのフェアリーチェスの駒に表記法を提供しており、^{[ 23 ]}チェスの標準的な代数表記法を拡張している。表記法は1つまたは2つの大文字、あるいは1つの大文字とそれに続く数字で構成される。標準的なナイトの表記法は文字S（ドイツ語のSpringer、跳躍者を意味する）であり、文字Nはナイトライダーを表すことは注目に値する。ワジールの表記法はWE（ドイツ語のWesir）であり、WAはワラン（ルーク+ナイトライダー）を表す。

ピースの相対的な価値

伝統的なチェスの駒の価値と同様に、妖精の駒にもスコアリングや戦略策定に用いるための価値が割り当てられています。チェスの様々な駒の相対的な価値に関する情報は豊富にありますが、数種類の駒以外について簡潔な形式でまとめられたリソースはほとんどありません。このような要約を作成する際の課題の一つは、駒の価値が、それらがプレイされる盤のサイズや、盤上の他の駒の組み合わせに依存することです。たとえ同じゲーム形式（盤のサイズや他の駒の組み合わせ）を想定していても、他の多くの駒の具体的な価値についてはほとんど合意が得られていません。

8×8の盤上では、標準的なチェスの駒（ポーン、ナイト、ビショップ、ルーク、クイーン）には通常、それぞれ1、3、3、5、9の値が与えられます。基本駒であるワジール（W）、フェルズ（F）、マン（WF = K）を同様の駒の組み合わせでプレイすると、通常はそれぞれ約1、1.5、3ポイントの値が与えられます。人気の複合駒であるアーチビショップ（BN）、チャンセラー（RN）、アマゾン（QN）の3つは、それぞれ約8、8.5、12ポイントの値が与えられると推定されています。その他の駒の価値は十分に確立されておらず、複合駒は構成駒の合計で近似される場合もあれば、相乗効果（アーチビショップとチャンセラーの場合など）により若干高く推定される場合もあります。

現代のチェスの変種であるマスケット銃士チェス^{[ 24 ]}は、タカ、ゾウ、ユニコーン、要塞、ドラゴン、スパイダー、ヒョウ、大砲、アーチビショップ、チャンセラーの 10 種類の妖精の駒の比較的正確な価値を算出しようと試みました。これらの計算に使用された方法は、開発された専用エンジンを使用した計算に基づいています。何千ものゲームが生成され、出発点となった値を改良するのに役立ちました (マスケット銃士チェスの駒の相対的価値^{[ 25 ]} )。他の独立したアプローチでは、マスケット銃士チェスが試されました。^{[ 26 ]}例えば、Sbiis Sabian は 24 ページの記事で、既存の多くの方法をレビューし、以前の試行からヒントを得て独自の方法論を考案しました。彼は、ランダムなチェスの位置を生成するプログラムを作成し、相対的な駒の価値を近似する何千もの位置での平均移動を計算しました。^{[ 26 ]}もう一つの進歩は強力なエンジンの使用である。グランドマスターのラリー・カウフマンが提示したアプローチは、ビショップペアなど多くの状況で相対的な駒の価値を評価することを可能にした。^{[ 27 ]}

ユニコード

回転した駒、等速ホッパー、ハイブリッドなど、多くのフェアリー駒のシンボルが、UnicodeブロックChess Symbolsで使用できます。

参照

• 妖精チェス
• 妖精のチェスの駒のリスト
• チェスの亜種
• 通信チェス
• オーソドックスな作品の動き
• さまざまな言語での正統派の曲名
• ペヌルティマ– 各ゲームごとに妖精の駒が発明されるチェスのバリエーション
• 3次元チェス-前述のラウムシャッハを含む複数のバリエーション

参考文献

1. 異端のチェスの駒に関するUnicode提案。Wayback Machineに2017年7月24日にアーカイブ。引用：「妖精の駒のほとんどは、慣例的に標準的なチェスの駒のシンボルを回転させることによって表現される。」（p. 1）、「常に正統な駒に対応する標準的な直立シンボルとは異なり、回転シンボルと特定の駒の種類の間には厳密な一対一の対応関係はない。使用される妖精の駒の数は無数であり、考えられる駒の数は無限である。代わりに、回転シンボルは必要に応じて駒に割り当てられ、作曲家は適切と思われるシンボルを幅広く選択できる。慣例によって固定されているのはごく少数のごく一般的なシンボルのみである…」（p. 2）、「これらの駒に独自のシンボルを使用することは、問題のあるチェスの愛好家よりも、前述の変種チェスのプレイヤーの間でより一般的である」（p. 6）。
2. ヴェリミロヴィッチ、M. Valtonen, K. (2012)、Encyclopedia of Chess 問題、Šahovski 情報提供者、p. 168
3. Wallace, Garth; Everson, Michael (2017年4月4日). 「UCSにおける異端のチェス記号のエンコードに関する改訂提案」(PDF) . unicode.org . Unicode . 2024年1月9日閲覧。
4. Bala, Gavin Jared; Miller, Kirk (2023年12月22日). 「Unicode request for shatranj symbol」(PDF) . unciode.org . Unicode . 2024年1月9日閲覧。
5. ディッキンズ、アンソニー・S・M (1969) [1967].『フェアリーチェス入門』（1971年ドーバー版第2版）リッチモンド（イギリス）、ニューヨーク：Qプレス（ドーバー）。ISBN 0-486-22687-5; 9, 30頁。
6. Poisson、「Categories de pièces – 作品の種類」、§「Bondisseur( m , n ) – ( m , n )Leaper」
7. 「Chu Shogi」 .
8. Poisson、「Pièces féeriques – 妖精の断片」、§§「アルフィル」および「フェルス」
9. 「JP・ジェリス『All the King's Men』」 2016年7月31日時点のオリジナルよりアーカイブ。 2010年7月20日閲覧。
10. 「JP Jelliss, Theory of Moves and Pieces」。2017年7月31日時点のオリジナルよりアーカイブ。2017年9月11日閲覧。
11. “P. Aronson and GW Duke, Complete Permutation Chess” . 2021年11月30日時点のオリジナルよりアーカイブ。2021年4月5日閲覧。
12. 「The Piececlopedia: Pawn」 .
13. “Piecelopedia: Orphan” . 2022年10月27日時点のオリジナルよりアーカイブ。 2022年10月27日閲覧。
14. フェアリーチェスのUnicode提案: L2/16-293 Archived 2017-07-24 at the Wayback Machine、 L2/17-034R3 Archived 2022-10-03 at the Wayback Machine
15. 「Rexマルチプレックス」。
16. 「鉄の騎士」。
17. 「宇宙戦争: ジュピター」。
18. Thunkspace (2020-07-22). 5Dチェスとマルチバースタイムトラベル。シーン：ガイド。ドラゴンは四角形に沿って任意の距離を移動できます。
19. パーレット、1999
20. Overby, Glenn, II (2003).「ベッツァ記法」Archived 2010-06-20 at the Wayback Machine . CVP .
21. ベッツァ、ラルフ. 「My Funny Notation」 .チェスのバリアント– chessvariants.comより。
22. 「XBetza」Wayback Machineで2017年6月20日にアーカイブ。GNU XBoard。
23. 「S. エマーソン著『フェアリーチェスの定義用語集』（PDF） . 2021年5月6日時点のオリジナルよりアーカイブ（PDF） 。 2021年4月15日閲覧。
24. 「ホームページ」 . www.musketeerchess.net . 2019年11月4日閲覧。
25. Haddad, Zied (2017年12月12日). 「マスケット銃チェス、駒の相対的価値」 .マスケット銃チェスゲーム、現代のチェスのバリエーション. 2019年11月4日閲覧。
26. Sabian, Sbiis. 「muskeetervalues - Recreomathematica」 . sites.google.com . 2020年3月31日時点のオリジナルよりアーカイブ。 2019年11月4日閲覧。
27. Kaufman, Larry (2008年11月17日). 「物質的不均衡の評価（IM Larry Kaufman著）」 . Chess.com . 2019年11月4日閲覧。

参考文献

• カゾー、ジャン＝ルイ、ノールトン、リック（2017年）『チェスの世界：世紀と文明を通じた発展と変遷』マクファーランド、ISBN 978-0-7864-9427-9。
• ディッキンズ、アンソニー・S・M（1969）[1967]. 『フェアリーチェス入門』 （1971年ドーバー出版、第2版）。リッチモンド、イギリス；ニューヨーク：Qプレス；ドーバー。ISBN 0-486-22687-5。
• カール・ファベル;ケンプ、チャールズ E. (1969)。Schach ohne Grenzen (TR Dawsons Märchenschach) = Chess Unlimited (TR Dawson's Fairy Chess) (ドイツ語と英語)。アーンフリード・ハウプト（カバーデザイン）。デュッセルドルフとケンプテン/アルゴイ、ドイツ: Walter Rau Verlag。ASIN  B0000BQXG3。OCLC  601619310。
• ギファード、ニコラス。アラン・ビエナベ（1993）。Le Guide des échecs。特性が完了しました。パリ: ロベール・ラフォン - ブカン。ページ 1173–1219。ISBN​​ 9782221059135。
• マレー、ハロルド・JR (1913). 『チェスの歴史』 オックスフォード:クラレンドン・プレス. ISBN 978-0-19-827403-2。リンク。
• パーレット、デイヴィッド（1999年）『オックスフォード・ボードゲームの歴史』オックスフォード：オックスフォード大学出版局。ISBN 0-19-212998-8。
• プリチャード、デイヴィッド・B. (1994). 『チェスのバリエーション百科事典』 ゴダルミング、イギリス: ゲームズ＆パズルズ出版. pp.  132–33 . ISBN 0-9524142-0-1。
• プリチャード, デイビッド・B. (2007). ビーズリー, ジョン・D. (編). 『チェスのバリエーション分類百科事典（第2版）』 ハーペンデン, イギリス: ジョン・ビーズリー. ISBN 978-0-9555168-0-1。
• シュミットバーガー、R. ウェイン (1992). 『クラシックゲームのための新しいルール』ニューヨーク: ジョン・ワイリー. ISBN 0-471-53621-0。

ウェブページ

• Bagley-Jones, Christine (2012). 「Fairy Pieces Part 1」 . CVP . 2021年3月16日閲覧。昔の将棋の変種から154個の駒。
• ベッツァ、ラルフ(1996–2000). 「My Funny Notation」 . CVP . 2006年5月13日閲覧。
• ボドランダー、ハンス・L.、ハウ、デイヴィッド、ドゥニホ、ファーガス編 (1995). 「CVPの索引ページ」チェス・バリアント・ページズ.. §§: 「ピースクロペディア」と「ピースに関する記事」。
• カゾー、ジャン＝ルイ (2000–2014). 「チェスの歴史」 .チェスの歴史: JL カゾーのチェスページ.また、「私のチェスのバリエーション」。
• デルジャンスキー、イヴァン・A. (2001). 「Eight by Eight の Who is Who」 . CVP .
• ハウ、デイヴィッド (2011). 「チェスのバリエーションの簡潔ガイド」 . CVP .
• ジェリス、ジョージ・P. (2002–2012). 「バリアントチェスガイド」 .メイヘマティクス.英国チェスバリアント協会. § 「キングスメン全員」 . 2010年7月20日閲覧。§§：「バリアントチェスゲーム」；「バリアントチェスの紹介」＆「シンプルなチェスのバリアント」 [PDF]（2010）
• ジェリス、ジョージ・P. (2000–2016). 「ナイトの旅ノート」 .メイヘマティクス. § 「国王の部下たち」 .§§: 「幾何学: 動きの理論」 ; 「歴史」および「その他の駒」。
• ポワソン、クリスチャン (2003–2011). 「Categories de pièces – Types of pieces」 . Problemesis (フランス語と英語) . 2008年4月18日閲覧.
• ポワソン、クリスチャン (2002–2006). 「妖精の小品 ― 妖精の小品」 . Problemesis (フランス語と英語) . 2008年4月18日閲覧.

外部リンク

• ピースクロペディア妖精のチェスの駒の広範なリスト、その歴史と動きの図
• イヴァン・A・デルジャンスキーが編集した「Eight by Eight」のWho is Whoは、駒の価値も表示しています。
• 汎用チェス駒作成システム駒の価値を見積もる簡単な方法
• バリアントチェスガイド：キングスメン