輪郭積分

複素解析の数学分野において、路積分は複素平面上の経路に沿って特定の積分を評価する方法である。^{[ 1 ] [ 2 ] [ 3 ]}

輪郭積分は複素解析法の一つである留数計算^{[ 4 ]}と密接な関係がある。

路面積分の用途の一つは、実変数法だけでは容易に求まらない実数直線に沿った積分を評価することである。また、物理学においても様々な応用がある。^{[ 5 ]}

輪郭積分法には次のものがあります:

• 複素平面上の曲線に沿った複素数値関数の直接積分
• コーシー積分公式の応用
• 留数定理の応用

これらの積分または合計を求めるために、1 つの方法を使用することも、これらの方法を組み合わせて使用​​することも、さまざまな制限プロセスを使用することもできます。

複素平面上の曲線

複素解析において、積分路は複素平面上の曲線の一種です。積分路積分において、積分路は積分を適切に定義できる曲線の正確な定義を提供します。複素平面上の曲線は、実数直線の閉区間から複素平面への連続関数として定義されます。 ${\displaystyle z:[a,b]\to \mathbb {C} }$

この曲線の定義は、曲線の直感的な概念と一致しますが、閉区間からの連続関数によるパラメータ化を含みます。このより正確な定義により、積分に有用な曲線となるためにはどのような特性を持つ必要があるかを検討することができます。以下の節では、積分可能な曲線の集合を、方向を与えられる有限個の連続曲線から構築できる曲線のみに絞り込みます。さらに、「断片」が互いに交差しないように制限し、各断片が有限の（零でない）連続微分を持つことを要求します。これらの要件は、ペンで描くなど、一連の均一で安定したストロークで描くことができる曲線のみを考慮する必要があるという要件に対応しています。ストロークは、曲線の新しい断片を始めるためだけに止まり、ペンを離す必要はありません。^{[ 6 ]}

方向付けられた滑らかな曲線

輪郭線は、しばしば有向滑らかな曲線によって定義される。^{[ 6 ]}これらは、輪郭線を構成する滑らかな曲線の「部分」の正確な定義を提供する。

滑らかな曲線とは、各点を一度だけ通過する（ zは1対1）ような、ゼロでない連続的な微分を持つ曲線のことである。ただし、端点が一致する曲線（ ）は例外となる可能性がある。端点が一致する場合、その曲線は閉じた曲線と呼ばれ、関数は他のすべての点で1対1であり、微分は指定された点（）で連続でなければならない。閉じていない滑らかな曲線は、しばしば滑らかな円弧と呼ばれる。^{[ 6 ]}${\displaystyle z:[a,b]\to \mathbb {C} }$ ${\displaystyle z(a)=z(b)}$ ${\displaystyle z'(a)=z'(b)}$

曲線の媒介変数表示により、曲線上の点の自然な順序付けが提供されます。はの前に来ます。これは、有向滑らかな曲線の概念につながります。特定の媒介変数表示から独立した曲線を考えるのが最も有用です。これは、同じ方向を持つ滑らかな曲線の同値類を考えることによって行うことができます。有向滑らかな曲線は、複素平面上の点の順序付き集合として定義することができ、これは (媒介変数表示に従って) 自然な順序で並んだ滑らかな曲線の像です。点のすべての順序付けが滑らかな曲線の自然な順序付けであるとは限らないことに注意してください。実際、与えられた滑らかな曲線には、そのような順序付けが 2 つしかありません。また、1 つの閉曲線は任意の点を端点として持つことができますが、滑らかな円弧では端点の選択肢は 2 つしかありません。 ${\displaystyle z(x)}$ ${\displaystyle z(y)}$ ${\displaystyle x<y}$

輪郭

等高線は、等高線積分を定義する曲線のクラスです。等高線とは、端点が一方向に一致するように一致した、有向滑らかな曲線の有限列から構成される有向曲線です。これは、 となるすべての に対して、 の終点が の始点と一致するような曲線列でなければなりません。これには、すべての有向滑らかな曲線が含まれます。また、複素平面上の単一の点も等高線とみなされます。記号 は、曲線をつなぎ合わせて新しい曲線を形成することを示すためによく使用されます。したがって、曲線 で構成される等高線は次のように表すことができます。${\displaystyle \gamma _{1},\dots ,\gamma _{n}}$ ${\displaystyle \gamma_{i}}$ ${\displaystyle \gamma_{i+1}}$ ${\displaystyle i}$ ${\displaystyle 1\leq i<n}$ ${\displaystyle +}$ ${\displaystyle \Gamma}$ ${\displaystyle n}$ $${\displaystyle \Gamma =\gamma _{1}+\gamma _{2}+\cdots +\gamma _{n}.}$$

等高線積分

複素関数の路面積分は、実数値関数の積分の一般化である。複素平面上の連続関数の場合、路面積分は線積分と同様に定義することができる。まず、有向滑らかな曲線に沿った積分を実数値パラメータ上の積分で定義する。より一般的な定義は、区間分割やリーマン積分と同様に、路面の分割によって与えることができる。どちらの場合も、路面上の積分は、その路面を構成する有向滑らかな曲線上の積分の和として定義される。 ${\displaystyle f:\mathbb {C} \to \mathbb {C} }$

連続関数の場合

このように路面積分を定義するには、まず実変数上の複素数値関数の積分を考える必要がある。実変数の複素数値関数を とする。 の実部と虚部はそれぞれ とと表記されることが多いため、 となる。 すると、複素数値関数の区間上の積分は次のように与えられる。 ${\displaystyle f:\mathbb {R} \to \mathbb {C} }$ ${\displaystyle t}$ ${\displaystyle f}$ ${\displaystyle u(t)}$ ${\displaystyle v(t)}$ $${\displaystyle f(t)=u(t)+iv(t).}$$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ $${\displaystyle {\begin{aligned}\int _{a}^{b}f(t)\,dt&=\int _{a}^{b}{\big (}u(t)+iv(t){\big )}\,dt\\&=\int _{a}^{b}u(t)\,dt+i\int _{a}^{b}v(t)\,dt.\end{aligned}}}$$

さて、輪郭積分を定義するために、 を有向滑らかな曲線上の連続関数とする。をその位数（方向）と一致する任意の媒介変数化とする。すると、 に沿った積分はと表され 、次のように与えられる^{[ 6 ]。}${\displaystyle f:\mathbb {C} \to \mathbb {C} }$ ${\displaystyle \gamma}$ ${\displaystyle z:[a,b]\to \mathbb {C} }$ ${\displaystyle \gamma}$ ${\displaystyle \gamma}$ $${\displaystyle \int _{\gamma }f(z)\,dz\,}$$ $${\displaystyle \int _{\gamma }f(z)\,dz:=\int _{a}^{b}f{\big (}z(t){\big )}z'(t)\,dt.}$$

この定義は明確に定義されている。つまり、結果は選択されたパラメータ化に依存しない。^{[ 6 ]}右辺の実積分が存在しない場合、 に沿った積分は存在しないと言われる。 ${\displaystyle \gamma}$

リーマン積分の一般化として

リーマン積分の複素変数関数への一般化は、実数関数に対する定義と完全に類似して行われます。有向滑らかな曲線の分割は、曲線上の有限かつ順序付けられた点の集合として定義されます。曲線上の積分は、分割上の点における関数値の有限和の極限であり、分割上の任意の2つの連続する点（2次元複素平面上）間の最大距離（メッシュとも呼ばれます）が0に近づく極限です。 ${\displaystyle \gamma}$ ${\displaystyle \gamma}$

直接的な方法

直接法では、多変数微積分における線積分の計算と同様の方法で積分を計算します。つまり、以下の方法を用います。

• 輪郭のパラメータ化

  輪郭は、実変数の微分可能な複素数値関数によってパラメータ化されるか、または輪郭が複数の部分に分割されて個別にパラメータ化されます。

• パラメータ化を積分関数に代入する

  パラメータ化を積分関数に代入すると、積分は 1 つの実変数の積分に変換されます。

• 直接評価

  積分は実変数積分に類似した方法で評価されます。

例

複素解析における基本的な結果は、⁠1/z⁠は2π iであり、ここで等高線の軌跡は単位円（または0を中心とする正の向きのジョルダン曲線）を反時計回りに横断したものとみなされる。単位円の場合、積分を直接評価する方法がある。 $${\displaystyle \oint _{C}{\frac {1}{z}}\,dz.}$$

この積分を評価するには、単位円| z | = 1 をz ( t ) = e ^it （ t ∈ [0, 2π] ）でパラメータ化した等高線として使用し、次のようにします。dz/dt⁠ =つまり^それと​ $${\displaystyle \oint _{C}{\frac {1}{z}}\,dz=\int _{0}^{2\pi }{\frac {1}{e^{it}}}ie^{it}\,dt=i\int _{0}^{2\pi }1\,dt=i\,t{\Big |}_{0}^{2\pi }=\left(2\pi -0\right)i=2\pi i}$$

これは積分の値です。この結果は、z が -1 乗されている場合にのみ適用されます。乗が -1 でない場合、結果は常にゼロになります。

積分定理の応用

積分定理の応用は、等高線に沿った等高線積分を評価するためにもよく使用されます。つまり、等高線積分の計算と同時に実数値積分も計算されます。

コーシーの積分公式や留数定理などの積分定理は、一般的に次のような方法で使用されます。

• 特定の輪郭が選択されます。

  積分路は、実数値積分を記述する複素平面の部分に沿っており、また、積分関数の特異点を囲んでいるため、コーシーの積分公式や留数定理を適用できるような曲線が選ばれる。

• コーシーの積分定理の応用

  積分は、各極の周りの小さな円の周りの積分のみに簡約されます。

• コーシーの積分公式または留数定理の応用

  これらの積分公式を適用すると、等高線全体の積分値が得られます。

• 等高線を実部と虚部に沿った等高線に分割する

  積分路全体は、先に選択した実数値積分を記述する複素平面上の部分（これをRとする）に沿う積分路と、複素平面を横切る積分路（これをIとする）に分けられる。積分路全体にわたる積分は、これらの積分路それぞれにおける積分の和となる。

• 複素平面を横切る積分は和に何ら影響を与えないことの証明

  積分I がゼロであることが証明できる場合、または求められている実数値積分が不適切である場合、上記の積分Iが 0 に近づくことを証明すれば、 Rに沿った積分は、輪郭R + Iの周りの積分に近づくことになります。

• 結論

  上記の手順を示すことができれば、実数値積分Rを直接計算できます。

例1

積分を考えてみよう $${\displaystyle \int _{-\infty }^{\infty }{\frac {1}{\left(x^{2}+1\right)^{2}}}\,dx,}$$

この積分を評価するために、複素数値関数を見る。 $${\displaystyle f(z)={\frac {1}{\left(z^{2}+1\right)^{2}}}}$$

iと− iに特異点を持つ。実数値積分を囲む積分路を選ぶ。ここでは実数直線（例えば− aからaへ向かう直線）上に境界直径を持つ半円が便利である。この積分路をCと呼ぶ。

処理には、コーシーの積分公式を使用する方法と留数法を使用する方法 の 2 つの方法があります。

コーシーの積分公式を用いる

注意してください: したがって $${\displaystyle \oint _{C}f(z)\,dz=\int _{-a}^{a}f(z)\,dz+\int _{\text{Arc}}f(z)\,dz}$$ $${\displaystyle \int _{-a}^{a}f(z)\,dz=\oint _{C}f(z)\,dz-\int _{\text{Arc}}f(z)\,dz}$$

さらに、 $${\displaystyle f(z)={\frac {1}{\left(z^{2}+1\right)^{2}}}={\frac {1}{(z+i)^{2}(zi)^{2}}}.}$$

輪郭の唯一の特異点は iにあるので、次のように書くことができる。 $${\displaystyle f(z)={\frac {\frac {1}{(z+i)^{2}}}{(zi)^{2}}},}$$

これにより、関数は式を直接適用できる形になります。そして、コーシーの積分公式を用いることで、 $${\displaystyle \oint _{C}f(z)\,dz=\oint _{C}{\frac {\frac {1}{(z+i)^{2}}}{(zi)^{2}}}\,dz=2\pi i\,\left.{\frac {d}{dz}}{\frac {1}{(z+i)^{2}}}\right|_{z=i}=2\pi i\left[{\frac {-2}{(z+i)^{3}}}\right]_{z=i}={\frac {\pi }{2}}}$$

上記の手順では、極が2次極であるため、1次微分を採用しています。つまり、( z − i )を2乗するので、f ( z )の1次微分を採用します。( z − i )を3乗する場合は、2次微分を採用し、2で割るなどします。( z − i )を1乗する場合は、0次微分、つまりf ( z )そのものに相当します。

推定補題を用いて、半円弧上の積分がa → ∞のときにゼロに近づくことを示す必要がある。$${\displaystyle \left|\int _{\text{Arc}}f(z)\,dz\right|\leq ML}$$

ここでMは弧に沿った| f ( z ) |の上限であり、 Lは弧の長さである 。 $${\displaystyle \left|\int _{\text{Arc}}f(z)\,dz\right|\leq {\frac {a\pi }{\left(a^{2}-1\right)^{2}}}\to 0{\text{ as }}a\to \infty .}$$ $${\displaystyle \int _{-\infty }^{\infty }{\frac {1}{\left(x^{2}+1\right)^{2}}}\,dx=\int _{-\infty }^{\infty }f(z)\,dz=\lim _{a\to +\infty }\int _{-a}^{a}f(z)\,dz={\frac {\pi }{2}}.\quad \square }$$

残余法を用いる

我々が考慮する必要がある唯一の特異点である iを中心としたf ( z )のローラン級数を考えてみましょう。すると、$${\displaystyle f(z)={\frac {-1}{4(z-i)^{2}}}+{\frac {-i}{4(z-i)}}+{\frac {3}{16}}+{\frac {i}{8}}(z-i)+{\frac {-5}{64}}(z-i)^{2}+\cdots }$$

(この級数の導出については、 ローラン級数からのサンプルのローラン計算を参照してください。)

検査により、残留物が以下のものであることは明らかである。私/4⁠なので、留数定理により、 $${\displaystyle \oint _{C}f(z)\,dz=\oint _{C}{\frac {1}{\left(z^{2}+1\right)^{2}}}\,dz=2\pi i\,\operatorname {Res} _{z=i}f(z)=2\pi i\left(-{\frac {i}{4}}\right)={\frac {\pi }{2}}\quad \square }$$

したがって、前と同じ結果が得られます。

輪郭ノート

余談ですが、半円は− iを囲むもう一つの特異点を含むとみなすべきではないかという疑問が生じます。実軸に沿った積分が正しい方向に動くためには、積分曲線は時計回り、つまり負の方向に進み、積分全体の符号を反転させる必要があります。

これは、系列による残余の方法の使用には影響しません。

例2 – コーシー分布

積分 $${\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx}$$

輪郭

（コーシー分布の特性関数のスカラー倍として確率論で現れる）は、初等微積分の手法では扱えない。これを、実数直線−aからaに沿って進み、その後、 0を中心とする半円に沿って反時計回りにaから−aまで進む曲線Cに沿った路面積分の極限として表すことで評価する。虚数単位iが曲線内に含まれる ように、 aは1より大きいものとする。路面積分は$${\displaystyle \int _{C}{\frac {e^{itz}}{z^{2}+1}}\,dz.}$$

e ^itzは整関数（複素平面上のどの点にも特異点を持たない関数）であるため、この関数^は分母z ² + 1がゼロとなる点においてのみ特異点を持つ。z 2 + 1 = ( z + i )( z − i ) であるので、これはz = iまたはz = − iの場合にのみ起こる。これらの点のうち、この等高線で囲まれた領域に含まれるのは1点だけである。f ( z )のz = iにおける留数は $${\displaystyle \lim _{z\to i}(z-i)f(z)=\lim _{z\to i}(z-i){\frac {e^{itz}}{z^{2}+1}}=\lim _{z\to i}(z-i){\frac {e^{itz}}{(z-i)(z+i)}}=\lim _{z\to i}{\frac {e^{itz}}{z+i}}={\frac {e^{-t}}{2i}}.}$$

留数定理によれば、 $${\displaystyle \int _{C}f(z)\,dz=2\pi i\operatorname {Res} _{z=i}f(z)=2\pi i{\frac {e^{-t}}{2i}}=\pi e^{-t}.}$$

輪郭線Cは「直線」部分と曲線の円弧に分割することができるので 、 $${\displaystyle \int _{\text{straight}}+\int _{\text{arc}}=\pi e^{-t},}$$ $${\displaystyle \int _{-a}^{a}=\pi e^{-t}-\int _{\text{arc}}.}$$

ジョルダンの補題によれば、t > 0の場合には$${\displaystyle \int _{\text{arc}}{\frac {e^{itz}}{z^{2}+1}}\,dz\rightarrow 0{\mbox{ as }}a\rightarrow \infty .}$$

したがって、t > 0の場合、$${\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx=\pi e^{-t}.}$$

iではなく− iの周りを回る弧を使った同様の議論から、t < 0の場合 、最終的に次のようになる ことがわかります。$${\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx=\pi e^{t},}$$ $${\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx=\pi e^{-|t|}.}$$

（t = 0の場合、積分は直ちに実数値計算法に帰着し、その値はπです。）

例3 – 三角関数の積分

三角関数を含む積分には特定の置換を行うことができ、その結果、積分は複素変数の有理関数に変換され、その後上記の方法を使用して積分を評価できます。

例として、 $${\displaystyle \int _{-\pi }^{\pi }{\frac {1}{1+3(\cos t)^{2}}}\,dt.}$$

z = e ^itの置き換えを試みよう。ここで 、 $${\displaystyle \cos t={\frac {1}{2}}\left(e^{it}+e^{-it}\right)={\frac {1}{2}}\left(z+{\frac {1}{z}}\right)}$$ $${\displaystyle {\frac {dz}{dt}}=iz,\ dt={\frac {dz}{iz}}.}$$

C を単位円と すると、次の式が得られます。

${\displaystyle {\begin{aligned}\oint _{C}{\frac {1}{1+3\left({\frac {1}{2}}\left(z+{\frac {1}{z}}\right)\right)^{2}}}\,{\frac {dz}{iz}}&=\oint _{C}{\frac {1}{1+{\frac {3}{4}}\left(z+{\frac {1}{z}}\right)^{2}}}{\frac {1}{iz}}\,dz\\&=\oint _{C}{\frac {-i}{z+{\frac {3}{4}}z\left(z+{\frac {1}{z}}\right)^{2}}}\,dz\\&=-i\oint _{C}{\frac {dz}{z+{\frac {3}{4}}z\left(z^{2}+2+{\frac {1}{z^{2}}}\right)}}\\&=-i\oint _{C}{\frac {dz}{z+{\frac {3}{4}}\left(z^{3}+2z+{\frac {1}{z}}\right)}}\\&=-i\oint _{C}{\frac {dz}{{\frac {3}{4}}z^{3}+{\frac {5}{2}}z+{\frac {3}{4z}}}}\\&=-i\oint _{C}{\frac {4}{3z^{3}+10z+{\frac {3}{z}}}}\,dz\\&=-4i\oint _{C}{\frac {dz}{3z^{3}+10z+{\frac {3}{z}}}}\\&=-4i\oint _{C}{\frac {z}{3z^{4}+10z^{2}+3}}\,dz\\&=-4i\oint _{C}{\frac {z}{3\left(z+{\sqrt {3}}i\right)\left(z-{\sqrt {3}}i\right)\left(z+{\frac {i}{\sqrt {3}}}\right)\left(z-{\frac {i}{\sqrt {3}}}\right)}}\,dz\\&=-{\frac {4i}{3}}\oint _{C}{\frac {z}{\left(z+{\sqrt {3}}i\right)\left(z-{\sqrt {3}}i\right)\left(z+{\frac {i}{\sqrt {3}}}\right)\left(z-{\frac {i}{\sqrt {3}}}\right)}}\,dz.\end{aligned}}}$

考慮すべき特異点は、C _{1 を}の周りの小円、C _{2 を}の周りの小円とすると、次のようになります。 ${\displaystyle {\tfrac {\pm i}{\sqrt {3}}}.}$ ${\displaystyle {\tfrac {i}{\sqrt {3}}},}$ ${\displaystyle {\tfrac {-i}{\sqrt {3}}}.}$ $${\displaystyle {\begin{aligned}&-{\frac {4i}{3}}\left[\oint _{C_{1}}{\frac {\frac {z}{\left(z+{\sqrt {3}}i\right)\left(z-{\sqrt {3}}i\right)\left(z+{\frac {i}{\sqrt {3}}}\right)}}{z-{\frac {i}{\sqrt {3}}}}}\,dz+\oint _{C_{2}}{\frac {\frac {z}{\left(z+{\sqrt {3}}i\right)\left(z-{\sqrt {3}}i\right)\left(z-{\frac {i}{\sqrt {3}}}\right)}}{z+{\frac {i}{\sqrt {3}}}}}\,dz\right]\\={}&-{\frac {4i}{3}}\left[2\pi i\left[{\frac {z}{\left(z+{\sqrt {3}}i\right)\left(z-{\sqrt {3}}i\right)\left(z+{\frac {i}{\sqrt {3}}}\right)}}\right]_{z={\frac {i}{\sqrt {3}}}}+2\pi i\left[{\frac {z}{\left(z+{\sqrt {3}}i\right)\left(z-{\sqrt {3}}i\right)\left(z-{\frac {i}{\sqrt {3}}}\right)}}\right]_{z=-{\frac {i}{\sqrt {3}}}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{\left({\frac {i}{\sqrt {3}}}+{\sqrt {3}}i\right)\left({\frac {i}{\sqrt {3}}}-{\sqrt {3}}i\right)\left({\frac {i}{\sqrt {3}}}+{\frac {i}{\sqrt {3}}}\right)}}+{\frac {-{\frac {i}{\sqrt {3}}}}{\left(-{\frac {i}{\sqrt {3}}}+{\sqrt {3}}i\right)\left(-{\frac {i}{\sqrt {3}}}-{\sqrt {3}}i\right)\left(-{\frac {i}{\sqrt {3}}}-{\frac {i}{\sqrt {3}}}\right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{\left({\frac {4}{\sqrt {3}}}i\right)\left(-{\frac {2}{i{\sqrt {3}}}}\right)\left({\frac {2}{{\sqrt {3}}i}}\right)}}+{\frac {-{\frac {i}{\sqrt {3}}}}{\left({\frac {2}{\sqrt {3}}}i\right)\left(-{\frac {4}{\sqrt {3}}}i\right)\left(-{\frac {2}{\sqrt {3}}}i\right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {i}{\sqrt {3}}}{i\left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}+{\frac {-{\frac {i}{\sqrt {3}}}}{-i\left({\frac {2}{\sqrt {3}}}\right)\left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{\left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}+{\frac {\frac {1}{\sqrt {3}}}{\left({\frac {2}{\sqrt {3}}}\right)\left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}+{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {3}{16}}+{\frac {3}{16}}\right]\\={}&\pi .\end{aligned}}}$$

例3a – 三角関数の積分、一般的な手順

上記の方法は、以下のタイプのすべての積分に適用できる。 $${\displaystyle \int _{0}^{2\pi }{\frac {P{\big (}\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t),\ldots {\big )}}{Q{\big (}\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t),\ldots {\big )}}}\,dt}$$

ここで、PとQは多項式、つまり三角関数の有理関数を積分するものです。積分の境界は、前の例のようにπと − π、あるいは 2 π離れた任意の端点のペアでもよいことに注意してください。

コツは、置換z = e ^itを使うことです。ここでdz = ie ^it dtなので、 $${\displaystyle {\frac {1}{iz}}\,dz=dt.}$$

この置換により、区間[0, 2π]が単位円に写像されます。さらに、 この 置換により zに関する 有理関数f ( z )が得られ、その積分はf ( z ) の留数を合計することで計算されます。$${\displaystyle \sin(kt)={\frac {e^{ikt}-e^{-ikt}}{2i}}={\frac {z^{k}-z^{-k}}{2i}}}$$ $${\displaystyle \cos(kt)={\frac {e^{ikt}+e^{-ikt}}{2}}={\frac {z^{k}+z^{-k}}{2}}}$$ $${\displaystyle \oint _{|z|=1}f(z){\frac {1}{iz}}\,dz}$$ 1/iz⁠単位円の内側。

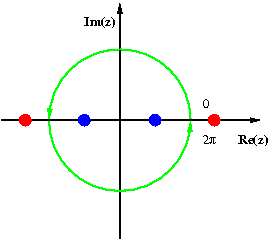
右の図はこれを示し、 これから計算します。最初のステップは、 $${\displaystyle I=\int _{0}^{\frac {\pi }{2}}{\frac {1}{1+(\sin t)^{2}}}\,dt,}$$ $${\displaystyle I={\frac {1}{4}}\int _{0}^{2\pi }{\frac {1}{1+(\sin t)^{2}}}\,dt.}$$

置換により $${\displaystyle {\frac {1}{4}}\oint _{|z|=1}{\frac {4iz}{z^{4}-6z^{2}+1}}\,dz=\oint _{|z|=1}{\frac {iz}{z^{4}-6z^{2}+1}}\,dz.}$$

この関数の極は1 ± √ 2と−1 ± √ 2にあります。これらのうち、1 + √ 2と−1 − √ 2は単位円の外側にあります（赤で表示、縮尺通りではありません）。一方、1 − √ 2と−1 + √ 2は単位円の内側にあります（青で表示）。対応する留数はどちらも− ⁠私√2​/16⁠、積分の値は $${\displaystyle I=2\pi i\;2\left(-{\frac {\sqrt {2}}{16}}i\right)=\pi {\frac {\sqrt {2}}{4}}.}$$

例4 – 分岐カット

実積分を考える $${\displaystyle \int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,dx.}$$

まず複素積分を定式化することから始めましょう $${\displaystyle \int _{C}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz=I.}$$

コーシーの積分公式または留数定理を再び用いて、適切な留数を得ることができます。ただし、重要なのは、z ^1/2 = e ^{(Log z )/2}であるため、z ^1/2には分岐切断があることです。これは、積分路Cの選択に影響します。通常、対数分岐切断は負の実軸として定義されますが、積分の計算が若干複雑になるため、ここでは正の実軸として定義します。

次に、いわゆるキーホール輪郭を使用します。これは、例えば半径εの原点を中心とする小円で構成され、正の実軸に平行でそれに近いが接触しない線分まで延長し、ほぼ完全な円まで延長し、負の方向に正の実軸に平行でそれに近い下の線分に戻り、中央の小円に戻ります。

z = −2とz = −4が大きな円の内側にあることに注意してください。これらは残りの2つの極であり、積分関数の分母を因数分解することで導出できます。z = 0の分岐点は原点を迂回することで回避されています。

γを半径εの小円、Γ を半径Rの大きい円とすると、 $${\displaystyle \int _{C}=\int _{\varepsilon }^{R}+\int _{\Gamma }+\int _{R}^{\varepsilon }+\int _{\gamma }.}$$

Γとγの積分は、 ε → 0およびR → ∞のときに両方ともゼロに近づくことが、上記の推定議論から示され、2つの項が残ります。ここで、 z ^1/2 = e ^{(Log z )/2}なので、分岐切断の外側の等高線上では、γに沿って2 π の偏角を得ています。（オイラーの恒等式により、e ^{i π は}単位ベクトルを表し、したがってその対数はπです。このπがzの偏角を意味します。⁠​​ の係数は1/2⁠ 2πを使うことを強制します。) だから $${\displaystyle {\begin{aligned}\int _{R}^{\varepsilon }{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz&=\int _{R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}\operatorname {Log} z}}{z^{2}+6z+8}}\,dz\\[6pt]&=\int _{R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}(\log |z|+i\arg {z})}}{z^{2}+6z+8}}\,dz\\[6pt]&=\int _{R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}\log |z|}e^{{\frac {1}{2}}(2\pi i)}}{z^{2}+6z+8}}\,dz\\[6pt]&=\int _{R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}\log |z|}e^{\pi i}}{z^{2}+6z+8}}\,dz\\[6pt]&=\int _{R}^{\varepsilon }{\frac {-{\sqrt {z}}}{z^{2}+6z+8}}\,dz\\[6pt]&=\int _{\varepsilon }^{R}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz.\end{aligned}}}$$

したがって： $${\displaystyle \int _{C}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz=2\int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,dx.}$$

留数定理またはコーシーの積分公式（最初に部分分数法を用いて2つの単純な積分の和を導出する）を用いると、次式が得られる。 $${\displaystyle \pi i\left({\frac {i}{\sqrt {2}}}-i\right)=\int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,dx=\pi \left(1-{\frac {1}{\sqrt {2}}}\right).\quad \square }$$

例5 – 対数の2乗

このセクションでは、 を例にした 積分のタイプを扱います 。$${\displaystyle \int _{0}^{\infty }{\frac {\log x}{\left(1+x^{2}\right)^{2}}}\,dx}$$

この積分を計算するには、関数 と、 −π < arg z ≤ π に対応する対数の枝を使用します。 $${\displaystyle f(z)=\left({\frac {\log z}{1+z^{2}}}\right)^{2}}$$

右に示すキーホール輪郭に沿ってf ( z )の積分を計算します。この積分は、計算したい最初の積分の倍数であり、コーシー留数定理により、

${\displaystyle {\begin{aligned}\left(\int _{R}+\int _{M}+\int _{N}+\int _{r}\right)f(z)\,dz=&\ 2\pi i{\big (}\operatorname {Res} _{z=i}f(z)+\operatorname {Res} _{z=-i}f(z){\big )}\\=&\ 2\pi i\left(-{\frac {\pi }{4}}+{\frac {1}{16}}i\pi ^{2}-{\frac {\pi }{4}}-{\frac {1}{16}}i\pi ^{2}\right)\\=&\ -i\pi ^{2}.\end{aligned}}}$

大きい円の半径をR、小さい円の半径をrとする。上側の直線をM、下側の直線をNで表す。前と同様に、 R → ∞かつr → 0の極限をとる。2つの円からの寄与はゼロとなる。例えば、ML補題を用いると、次のような上限が得られる。 $${\displaystyle \left|\int _{R}f(z)\,dz\right|\leq 2\pi R{\frac {(\log R)^{2}+\pi ^{2}}{\left(R^{2}-1\right)^{2}}}\to 0.}$$

MとNの寄与を計算するために、Mではz = − x + iε、Nではz = − x − iεと設定します（0 < x < ∞）。

${\displaystyle {\begin{aligned}-i\pi ^{2}&=\left(\int _{R}+\int _{M}+\int _{N}+\int _{r}\right)f(z)\,dz\\[6pt]&=\left(\int _{M}+\int _{N}\right)f(z)\,dz&&\int _{R},\int _{r}{\mbox{ vanish}}\\[6pt]&=-\int _{\infty }^{0}\left({\frac {\log(-x+i\varepsilon )}{1+(-x+i\varepsilon )^{2}}}\right)^{2}\,dx-\int _{0}^{\infty }\left({\frac {\log(-x-i\varepsilon )}{1+(-x-i\varepsilon )^{2}}}\right)^{2}\,dx\\[6pt]&=\int _{0}^{\infty }\left({\frac {\log(-x+i\varepsilon )}{1+(-x+i\varepsilon )^{2}}}\right)^{2}\,dx-\int _{0}^{\infty }\left({\frac {\log(-x-i\varepsilon )}{1+(-x-i\varepsilon )^{2}}}\right)^{2}\,dx\\[6pt]&=\int _{0}^{\infty }\left({\frac {\log x+i\pi }{1+x^{2}}}\right)^{2}\,dx-\int _{0}^{\infty }\left({\frac {\log x-i\pi }{1+x^{2}}}\right)^{2}\,dx&&\varepsilon \to 0\\&=\int _{0}^{\infty }{\frac {(\log x+i\pi )^{2}-(\log x-i\pi )^{2}}{\left(1+x^{2}\right)^{2}}}\,dx\\[6pt]&=\int _{0}^{\infty }{\frac {4\pi i\log x}{\left(1+x^{2}\right)^{2}}}\,dx\\[6pt]&=4\pi i\int _{0}^{\infty }{\frac {\log x}{\left(1+x^{2}\right)^{2}}}\,dx\end{aligned}}}$

これにより $${\displaystyle \int _{0}^{\infty }{\frac {\log x}{\left(1+x^{2}\right)^{2}}}\,dx=-{\frac {\pi }{4}}.}$$

例6 – 対数と無限大における留数

私たちは評価しようとしています $${\displaystyle I=\int _{0}^{3}{\frac {x^{\frac {3}{4}}(3-x)^{\frac {1}{4}}}{5-x}}\,dx.}$$

これには、 $${\displaystyle f(z)=z^{\frac {3}{4}}(3-z)^{\frac {1}{4}}.}$$

f ( z ) を、図の赤線で示すように[0, 3]に分岐を持つように構成します。そのために、対数の2つの枝を選び 、 $${\displaystyle z^{\frac {3}{4}}=\exp \left({\frac {3}{4}}\log z\right)\quad {\mbox{where }}-\pi \leq \arg z<\pi }$$ $${\displaystyle (3-z)^{\frac {1}{4}}=\exp \left({\frac {1}{4}}\log(3-z)\right)\quad {\mbox{where }}0\leq \arg(3-z)<2\pi .}$$

したがって、z ^{3 ⁄ 4}のカットは(−∞, 0]であり、 (3 − z ) ^1/4のカットは(−∞, 3]です。2つの積、つまりf ( z )のカットが[0, 3]であることは簡単にわかります。なぜなら、 f ( z )は実際には(−∞, 0)にわたって連続しているからです。これは、z = − r < 0で上からカットに近づくと、f ( z )が次の値を持つ ためです。$${\displaystyle r^{\frac {3}{4}}e^{{\frac {3}{4}}\pi i}(3+r)^{\frac {1}{4}}e^{{\frac {2}{4}}\pi i}=r^{\frac {3}{4}}(3+r)^{\frac {1}{4}}e^{{\frac {5}{4}}\pi i}.}$$

下から近づくと、f ( z )の値は $${\displaystyle r^{\frac {3}{4}}e^{-{\frac {3}{4}}\pi i}(3+r)^{\frac {1}{4}}e^{{\frac {0}{4}}\pi i}=r^{\frac {3}{4}}(3+r)^{\frac {1}{4}}e^{-{\frac {3}{4}}\pi i}.}$$

しかし $${\displaystyle e^{-{\frac {3}{4}}\pi i}=e^{{\frac {5}{4}}\pi i},}$$

こうすることで、切断面全体で連続性が保たれます。これは図に示されており、2つの黒い円には、 z ^{3 ⁄ 4}と(3 − z ) ^1/4で使用される対数の引数の対応する値がラベル付けされています。

図の緑色で示された等高線を使用します。そのためには、切断面のすぐ上とすぐ下の線分に沿って f ( z )の値を計算する必要があります。

z = rとします（極限、つまり2つの緑の円が半径0に縮むとき）（0 ≤ r ≤ 3）。上側の線分に沿って、f ( z )は値を持ち 、下側の線分に沿って、 $${\displaystyle r^{\frac {3}{4}}e^{{\frac {0}{4}}\pi i}(3-r)^{\frac {1}{4}}e^{{\frac {2}{4}}\pi i}=ir^{\frac {3}{4}}(3-r)^{\frac {1}{4}}}$$ $${\displaystyle r^{\frac {3}{4}}e^{{\frac {0}{4}}\pi i}(3-r)^{\frac {1}{4}}e^{{\frac {0}{4}}\pi i}=r^{\frac {3}{4}}(3-r)^{\frac {1}{4}}.}$$

⁠の積分はf ( z )/5 − z⁠上側のセグメントでは極限で− iIとなり、下側のセグメントではI となります。

2つの緑色の円に沿った積分が極限でゼロになることを示すことができれば、コーシー留数定理によりIの値も得られます。緑色の円の半径をρ （ ρ < 0.001、ρ → 0）とし、最尤不等式を適用します。左側の 円C _{Lについては、}$${\displaystyle \left|\int _{C_{\mathrm {L} }}{\frac {f(z)}{5-z}}dz\right|\leq 2\pi \rho {\frac {\rho ^{\frac {3}{4}}3.001^{\frac {1}{4}}}{4.999}}\in {\mathcal {O}}\left(\rho ^{\frac {7}{4}}\right)\to 0.}$$

同様に、右側の 円C _{Rについては、}$${\displaystyle \left|\int _{C_{\mathrm {R} }}{\frac {f(z)}{5-z}}dz\right|\leq 2\pi \rho {\frac {3.001^{\frac {3}{4}}\rho ^{\frac {1}{4}}}{1.999}}\in {\mathcal {O}}\left(\rho ^{\frac {5}{4}}\right)\to 0.}$$

コーシー留数定理を用いると、 以下の式が得られます。マイナス符号は留数の周りを時計回りに回っているためです。先ほどの対数の枝を用いると、明らかに $${\displaystyle (-i+1)I=-2\pi i\left(\operatorname {Res} _{z=5}{\frac {f(z)}{5-z}}+\operatorname {Res} _{z=\infty }{\frac {f(z)}{5-z}}\right).}$$ $${\displaystyle \operatorname {Res} _{z=5}{\frac {f(z)}{5-z}}=-5^{\frac {3}{4}}e^{{\frac {1}{4}}\log(-2)}.}$$

図では極は青で示されています。値は次のように簡略化されます。 $${\displaystyle -5^{\frac {3}{4}}e^{{\frac {1}{4}}(\log 2+\pi i)}=-e^{{\frac {1}{4}}\pi i}5^{\frac {3}{4}}2^{\frac {1}{4}}.}$$

無限大における剰余については次の式を使用します。 $${\displaystyle \operatorname {Res} _{z=\infty }h(z)=\operatorname {Res} _{z=0}\left(-{\frac {1}{z^{2}}}h\left({\frac {1}{z}}\right)\right).}$$

を代入すると、 そして、 対数の第二枝として −1 = e ^{π i} という事実を用いたことがわかります。次に二項展開を適用して、$${\displaystyle {\frac {1}{5-{\frac {1}{z}}}}=-z\left(1+5z+5^{2}z^{2}+5^{3}z^{3}+\cdots \right)}$$ $${\displaystyle \left({\frac {1}{z^{3}}}\left(3-{\frac {1}{z}}\right)\right)^{\frac {1}{4}}={\frac {1}{z}}(3z-1)^{\frac {1}{4}}={\frac {1}{z}}e^{{\frac {1}{4}}\pi i}(1-3z)^{\frac {1}{4}},}$$ $${\displaystyle {\frac {1}{z}}e^{{\frac {1}{4}}\pi i}\left(1-{1/4 \choose 1}3z+{1/4 \choose 2}3^{2}z^{2}-{1/4 \choose 3}3^{3}z^{3}+\cdots \right).}$$

結論としては $${\displaystyle \operatorname {Res} _{z=\infty }{\frac {f(z)}{5-z}}=e^{{\frac {1}{4}}\pi i}\left(5-{\frac {3}{4}}\right)=e^{{\frac {1}{4}}\pi i}{\frac {17}{4}}.}$$

最終的に、 Iの値は 次式 となる。$${\displaystyle I=2\pi i{\frac {e^{{\frac {1}{4}}\pi i}}{-1+i}}\left({\frac {17}{4}}-5^{\frac {3}{4}}2^{\frac {1}{4}}\right)=2\pi 2^{-{\frac {1}{2}}}\left({\frac {17}{4}}-5^{\frac {3}{4}}2^{\frac {1}{4}}\right)}$$ $${\displaystyle I={\frac {\pi }{2{\sqrt {2}}}}\left(17-5^{\frac {3}{4}}2^{\frac {9}{4}}\right)={\frac {\pi }{2{\sqrt {2}}}}\left(17-40^{\frac {3}{4}}\right).}$$

留数定理による評価

留数定理を用いることで、閉路積分を評価することができます。以下は、留数定理を用いて閉路積分を評価する例です。

留数定理を使ってこの輪郭積分を評価してみましょう。 $${\displaystyle \oint _{C}{\frac {e^{z}}{z^{3}}}\,dz}$$

留数定理は次のように述べている。 $${\displaystyle \oint _{C}f(z)dz=2\pi i\cdot \sum \operatorname {Res} (f,a_{k})}$$

ここで、 は の留数、 はの輪郭線内に存在するの特異点です（ 上に直接存在するものは存在しません）。 ${\displaystyle \operatorname {Res} }$ ${\displaystyle f(z)}$ ${\displaystyle a_{k}}$ ${\displaystyle f(z)}$ ${\displaystyle C}$ ${\displaystyle C}$

${\displaystyle f(z)}$ は極を1つしか持たない。このことから、の留数は${\displaystyle 0}$ ${\displaystyle f(z)}$ ${\displaystyle {\tfrac {1}{2}}}$ $${\displaystyle {\begin{aligned}\oint _{C}f(z)dz&=\oint _{C}{\frac {e^{z}}{z^{3}}}dz\\&=2\pi i\cdot \operatorname {Res} _{z=0}f(z)\\&=2\pi i\operatorname {Res} _{z=0}{\frac {e^{z}}{z^{3}}}\\&=2\pi i\cdot {\frac {1}{2}}\\&=\pi i\end{aligned}}}$$

したがって、留数定理を使用して、次のことを決定できます。 $${\displaystyle \oint _{C}{\frac {e^{z}}{z^{3}}}dz=\pi i.}$$

多変数等高線積分

多変数の等高線積分（すなわち、面積分、複素体積積分、高階積分）を解くには、発散定理を用いる必要があります。ここでは、を と交換可能とします。これらはどちらも、 で表されるベクトル場の発散として機能します。この定理は以下を述べています。 ${\displaystyle \nabla \cdot }$ ${\displaystyle \operatorname {div} }$ ${\displaystyle \mathbf {F} }$ $${\displaystyle \underbrace {\int \cdots \int _{U}} _{n}\operatorname {div} (\mathbf {F} )\,dV=\underbrace {\oint \cdots \oint _{\partial U}} _{n-1}\mathbf {F} \cdot \mathbf {n} \,dS}$$

さらに、の別の表記である を評価する必要もあります。任意の次元の発散は次のように記述できます。 ${\displaystyle \nabla \cdot \mathbf {F} }$ ${\displaystyle \nabla \cdot \mathbf {F} }$ ${\displaystyle \operatorname {div} (\mathbf {F} )}$ $${\displaystyle {\begin{aligned}\operatorname {div} (\mathbf {F} )&=\nabla \cdot \mathbf {F} \\&=\left({\frac {\partial }{\partial u}},{\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}},\dots \right)\cdot (F_{u},F_{x},F_{y},F_{z},\dots )\\&=\left({\frac {\partial F_{u}}{\partial u}}+{\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}+\cdots \right)\end{aligned}}}$$

例1

ベクトル場 とを次の式で囲むとする。 ${\displaystyle \mathbf {F} =\sin(2x)\mathbf {e} _{x}+\sin(2y)\mathbf {e} _{y}+\sin(2z)\mathbf {e} _{z}}$ $${\displaystyle {0\leq x\leq 1}\quad {0\leq y\leq 3}\quad {-1\leq z\leq 4}}$$

対応する二重等高線積分は次のように設定されます。

${\displaystyle }$ ${\displaystyle {\scriptstyle S}}$ ${\displaystyle \mathbf {F} \cdot \mathbf {n} \,dS}$

ここで を評価します。同時に、対応する三重積分を設定します。 ${\displaystyle \nabla \cdot \mathbf {F} }$ $${\displaystyle {\begin{aligned}&=\iiint _{V}\left({\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}\right)dV\\[6pt]&=\iiint _{V}\left({\frac {\partial \sin(2x)}{\partial x}}+{\frac {\partial \sin(2y)}{\partial y}}+{\frac {\partial \sin(2z)}{\partial z}}\right)dV\\[6pt]&=\iiint _{V}2\left(\cos(2x)+\cos(2y)+\cos(2z)\right)dV\\[6pt]&=\int _{0}^{1}\int _{0}^{3}\int _{-1}^{4}2(\cos(2x)+\cos(2y)+\cos(2z))\,dx\,dy\,dz\\[6pt]&=\int _{0}^{1}\int _{0}^{3}(10\cos(2y)+\sin(8)+\sin(2)+10\cos(z))\,dy\,dz\\[6pt]&=\int _{0}^{1}(30\cos(2z)+3\sin(2)+3\sin(8)+5\sin(6))\,dz\\[6pt]&=18\sin(2)+3\sin(8)+5\sin(6)\end{aligned}}}$$

例2

ベクトル場 を とし、この場合、パラメータは4つあることに注意する。このベクトル場が以下の式で囲まれるとする。 ${\displaystyle \mathbf {F} =u^{4}\mathbf {e} _{u}+x^{5}\mathbf {e} _{x}+y^{6}\mathbf {e} _{y}+z^{-3}\mathbf {e} _{z}}$ $${\displaystyle {0\leq x\leq 1}\quad {-10\leq y\leq 2\pi }\quad {4\leq z\leq 5}\quad {-1\leq u\leq 3}}$$

これを評価するには、前述の発散定理を利用し、を評価する必要があります。${\displaystyle \nabla \cdot \mathbf {F} }$ ${\displaystyle dV=dx\,dy\,dz\,du}$

${\displaystyle {\scriptstyle S}}$ ${\displaystyle \mathbf {F} \cdot \mathbf {n} \,dS}$

$${\displaystyle {\begin{aligned}&=\iiiint _{V}\left({\frac {\partial F_{u}}{\partial u}}+{\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}\right)\,dV\\[6pt]&=\iiiint _{V}\left({\frac {\partial u^{4}}{\partial u}}+{\frac {\partial x^{5}}{\partial x}}+{\frac {\partial y^{6}}{\partial y}}+{\frac {\partial z^{-3}}{\partial z}}\right)\,dV\\[6pt]&=\iiiint _{V}{\frac {4u^{3}z^{4}+5x^{4}z^{4}+5y^{4}z^{4}-3}{z^{4}}}\,dV\\[6pt]&=\iiiint _{V}{\frac {4u^{3}z^{4}+5x^{4}z^{4}+5y^{4}z^{4}-3}{z^{4}}}\,dV\\[6pt]&=\int _{0}^{1}\int _{-10}^{2\pi }\int _{4}^{5}\int _{-1}^{3}{\frac {4u^{3}z^{4}+5x^{4}z^{4}+5y^{4}z^{4}-3}{z^{4}}}\,dV\\[6pt]&=\int _{0}^{1}\int _{-10}^{2\pi }\int _{4}^{5}\left({\frac {4(3u^{4}z^{3}+3y^{6}+91z^{3}+3)}{3z^{3}}}\right)\,dy\,dz\,du\\[6pt]&=\int _{0}^{1}\int _{-10}^{2\pi }\left(4u^{4}+{\frac {743440}{21}}+{\frac {4}{z^{3}}}\right)\,dz\,du\\[6pt]&=\int _{0}^{1}\left(-{\frac {1}{2\pi ^{2}}}+{\frac {1486880\pi }{21}}+8\pi u^{4}+40u^{4}+{\frac {371720021}{1050}}\right)\,du\\[6pt]&={\frac {371728421}{1050}}+{\frac {14869136\pi ^{3}-105}{210\pi ^{2}}}\\[6pt]&\approx {576468.77}\end{aligned}}}$$

したがって、 の等高線積分を評価できます。 の任意のベクトル場に対しても、同じ方法で等高線積分を評価できます。 ${\displaystyle n=4}$ ${\displaystyle n>4}$

積分表現

複素解析において、積分表現は関数を複素平面上の線積分として表す。このような表現は正則関数の理論において中心的な役割を果たし、複素積分の基本定理と密接に結びついている。

最も重要な例の 1 つは、コーシーの積分公式です。これは、解析関数を周囲の輪郭上の値から 再構築する方法を提供します。

${\displaystyle f(z)={\frac {1}{2\pi i}}\oint _{\gamma }{\frac {f(\zeta )}{\zeta -z}}\,d\zeta }$

ここで、 は単純閉曲線 上および 内部の正則関数、は 内部の点、は積分変数です。この式は、曲線内部の の値は、 曲線に沿った の値によって決まることを示しています。 ${\displaystyle f}$ ${\displaystyle \gamma }$ ${\displaystyle z}$ ${\displaystyle \gamma }$ ${\displaystyle \zeta }$ ${\displaystyle f}$

例

逆ラプラス変換

逆ラプラス変換は、ブロムウィッチ積分と呼ばれる複素積分によって定義されます。

${\displaystyle f(t)={\frac {1}{2\pi i}}\int _{\gamma -i\infty }^{\gamma +i\infty }e^{st}F(s)\,ds}$

この積分は関数をそのラプラス変換で表現します。 ${\displaystyle f(t)}$ ${\displaystyle F(s)}$

シンク関数表現

次の積分はsinc関数の表現を与えます。

${\displaystyle {\frac {\sin x}{x}}={\frac {1}{\pi }}\int _{0}^{\infty }\cos(xt)\,dt}$

これは実積分ですが、その導出や評価には、しばしば等高線積分の手法が使用されます。

ガンマ関数

ガンマ関数の積分表現は次のようになります。

${\displaystyle \Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}\,dt\quad {\text{for }}\operatorname {Re} (z)>0}$

この定義の拡張には複素平面上の等高線積分が含まれます。

リーマンゼータ関数

ディリクレ級数によるリーマンゼータ関数 の元々の定義は、 ${\displaystyle \zeta (s)}$

${\displaystyle \zeta (s)=\sum _{k=1}^{\infty }{\frac {1}{k^{s}}}}$ 、

は にのみ有効ですが、 ${\displaystyle \operatorname {Re} (s)>1}$

${\displaystyle \zeta (s)={\dfrac {\Gamma (1-s)}{2\pi i}}\int _{H}{\dfrac {(-t)^{s-1}}{e^{t}-1}}dt}$ 、

ここで、積分はハンケル曲線 上で行われ、と等しくないすべての複素数 に対して有効です。 ${\displaystyle H}$ ${\displaystyle s}$ ${\displaystyle 1}$

アプリケーション

積分表現は、定積分を評価したり、関数恒等式を導出したり、微分方程式を解いたりするのに用いられます。また、複素漸近解析、ポテンシャル理論、数理物理学にも登場します。

参照

• 残差（複素解析）
• コーシー主値
• ポアソン積分
• ポッホハマー輪郭

参考文献

1. ストーカー、ジョン（1998年）『複素解析：古典関数理論の基礎』シュプリンガー、p.77、ISBN 0-8176-4038-X。
2. Bak, Joseph; Newman, Donald J. (1997). 「第11章と第12章」 .複素解析. Springer. pp.  130– 156. ISBN 0-387-94756-6。
3. クランツ、スティーブン・ジョージ (1999). 「第2章」 .複素変数ハンドブック. シュプリンガー. ISBN 0-8176-4011-8。
4. ミトリノヴィッチ, ドラゴスラフ・S.; ケチキッチ, ヨヴァン・D. (1984). 「第2章」コーシー留数法：理論と応用. シュプリンガー. ISBN 90-277-1623-4。
5. ミトリノヴィッチ, ドラゴスラフ・S.; ケチキッチ, ヨヴァン・D. (1984). 「第5章」.コーシー留数法：理論と応用. シュプリンガー. ISBN 90-277-1623-4。
6. サフ, エドワード・B.; スナイダー, アーサー・デイヴィッド (2003). 「第4章」.複素解析の基礎と工学、科学、数学への応用（第3版）. プレンティス・ホール. ISBN 0-1390-7874-6。

さらに読む

• ティッチマーシュ, EC (1939)、『関数論』（第2版）、オックスフォード大学出版局; 1968年再版、ISBN 0-19-853349-7
• Marko Riedel 他、Problème d'intégrale、Les-Mathematiques.net、フランス語。
• Marko Riedel 他、「剰余による積分」、math.stackexchange.com。
• WWL チェン『複素解析入門』
• さまざまな著者、sin límites ni cotas、es.ciencia.matematicas、スペイン語。

外部リンク

• 「複素積分法」、数学百科事典、EMS Press、2001 [1994]