傾き
傾斜m＝ΔyΔx＝tan⁡（θ）{\displaystyle m={\frac {\Delta y}{\Delta x}}=\tan(\theta)}

数学において、直線の傾斜または勾配は、平面上の直線の方向を表す数値です。[ 1 ]傾斜は、しばしば文字mで表され、直線上の2つの異なる点間の垂直方向の変化と水平方向の変化（「上昇/下降」）の比率として計算され、同じ勾配を与えます。傾斜とは、2点間の垂直距離（上昇）と水平距離（下降）の比率であり、任意の点を選択した場合の直線距離や直角ではありません。説明すると、傾斜とは、 2点間の垂直距離（上昇）と水平距離（下降）の比率であり、直距離や直角ではありません。直線は、道路測量士 によって設定された物理的なもの、道路や屋根の図面のような絵画的なもの、または抽象的なものとなる場合があります。 数学的概念の応用は、地理学や土木工学における勾配または勾配に見られます

直線の傾き、勾配、または勾配は、その傾きの絶対値です。絶対値が大きいほど、直線の勾配が急であることを示します。直線の傾向は次のように定義されます。

  • 「増加」または「上昇」する線は左から右に上がり、正の傾きを持ちます。m＞0{\displaystyle m>0}
  • 「減少」または「下降」線は左から右に下がり、負の傾きを持ちます。m<0{\displaystyle m<0}

特別な方向は次のとおりです。

  • 「（正方形の）対角線」の直線の傾きは1ですm＝1{\displaystyle m=1}
  • 「水平」線（定数関数のグラフ）の傾きは 0 です。m＝0{\displaystyle m=0}
  • 「垂直」線は、定義されていない、または無限の傾斜を持ちます (以下を参照)。

道路上の2点の標高がそれぞれy 1とy 2の場合、その差は ( y 2 − y 1 ) = Δ yです。地球の曲率を無視すると、2点間の水平距離が固定点からx 1とx 2の場合、勾配は ( x 2 − x 1 ) = Δ xです。2点間の勾配は、その差の比です。

m＝ΔyΔx＝y2−y1x2−x1。{\displaystyle m={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.}}

三角法によれば、直線の傾きmは、その傾斜角θと正接関数によって関係づけられる。

m＝tan⁡（θ）。{\displaystyle m=\tan(\theta ).}

したがって、45°の上昇線の傾きはm = +1 となり、45°の下降線の傾きはm = −1 となります。

これを一般化すると、微分積分学では、平面曲線のある点における傾きを、その点における接線の傾きとして定義します。曲線を複数の点で近似する場合、曲線の傾きは、隣接する2点間の割線の傾きで近似できます。曲線が代数式のグラフとして与えられる場合、微積分学は各点における傾きの公式を与えます。このように、傾きは微積分学とその設計への応用における中心的な概念の一つです。

表記法

傾きを表すのに文字mが使われる理由については明確な答えはないようですが、英語でmが初めて登場したのは、直線の方程式を「y = mx + b」と導入したオブライエン（1844）[ 2 ]です。また、トッドハンター（1888）[ 3 ]も「y = mx + c」と記しています。[ 4 ]

定義

y = (3/2) x − 1の傾きを図解しています。クリックして拡大してください
座標系における直線の傾き、f ( x ) = −12 x + 2からf ( x ) = 12 x + 2まで

x軸とy軸を含む平面上の直線の傾きは、一般的に文字mで表され[ 5 ]、直線上の2つの異なる点間のy座標の変化をx座標の対応する変化で割ったものとして定義されます。これは次の式で表されます。

m＝ΔyΔx＝垂直変化水平変化＝上昇走行。{\displaystyle m={\frac {\Delta y}{\Delta x}}={\frac {{\text{垂直}}\,{\text{変化}}}{{\text{水平}}\,{\text{変化}}}}={\frac {\text{上昇}}{\text{走行}}}.}}

(ギリシャ文字のデルタΔ は、数学では一般的に「違い」や「変化」を意味します。)

2点とが与えられている場合、一方から他方への の変化は（増加）であり、 の変化は（上昇）です。両方の量を上記の式に代入すると、以下の式が得られます。 （x1、y1）{\displaystyle (x_{1},y_{1})}（x2、y2）{\displaystyle (x_{2},y_{2})}x{\displaystyle x}x2−x1{\displaystyle x_{2}-x_{1}}y{\displaystyle y}y2−y1{\displaystyle y_{2}-y_{1}}

m＝y2−y1x2−x1。{\displaystyle m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}

この式は、軸に平行な垂直線（ゼロ除算を参照）では成立しません。垂直線では、傾きが無限大とみなされるため、垂直線の傾きは未定義とみなされます。 y{\displaystyle y}

例

2点P  = (1, 2)とQ = (13, 8)を通る直線があるとします 。-座標の差を-座標の差で割ることで、直線の傾きを求めることができます y{\displaystyle y}x{\displaystyle x}

m＝ΔyΔx＝y2−y1x2−x1＝（8−2）（13−1）＝612＝12。{\displaystyle m={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}={\frac {(8-2)}{(13-1)}}={\frac {6}{12}}={\frac {1}{2}}.}
傾きが正なので、直線の方向は増加しています。| m | < 1 なので、傾斜はそれほど急ではありません（傾斜 < 45°）。

別の例として、点(4, 15)と点(3, 21)を通る直線を考えてみましょう。この直線の傾きは

m＝21−153−4＝6−1＝−6.{\displaystyle m={\frac {21-15}{3-4}}={\frac {6}{-1}}=-6.}
傾きが負なので、直線の方向は下降しています。| m | > 1 なので、この下降はかなり急です（下降角 > 45°）。

代数と幾何学

平行線と垂直線の傾き
  • が の線形関数である場合、 の係数は関数をプロットすることによって作成された直線の傾きです。したがって、直線の方程式が次のように表される場合 y{\displaystyle y}x{\displaystyle x}x{\displaystyle x}
    y＝mx＋b{\displaystyle y=mx+b}
    は傾きです。直線の方程式のこの形式は傾き切片形式と呼ばれます。これは、直線のy切片、つまり直線が軸と交差する座標として解釈できるためです。m{\displaystyle m}b{\displaystyle b}y{\displaystyle y}y{\displaystyle y}
  • 直線の傾きと直線上の点が両方とも分かっている場合、点-傾きの公式を使用して直線の方程式を見つけることができます。 m{\displaystyle m}(x1,y1){\displaystyle (x_{1},y_{1})}
    y−y1=m(x−x1).{\displaystyle y-y_{1}=m(x-x_{1}).}
  • 線形方程式によって定義される直線の傾き
    ax+by+c=0{\displaystyle ax+by+c=0}
    は
    −ab{\displaystyle -{\frac {a}{b}}}。
  • 2本の直線が平行であるためには、それらが同じ直線（一致）ではなく、かつ、それらの傾きが等しいか、または両方とも垂直で、したがって両方とも傾きが定義されていない場合に限ります
  • 2 本の直線の傾きの積が -1 であるか、一方の直線の傾きが 0 (水平線) でもう一方の直線の傾きが定義されていない場合 (垂直線)、2 本の直線は垂直になります。
  • 直線がx軸となす角度 θ (-90° から 90° の間) は、傾きmと次のように関係します。
    m=tan⁡(θ){\displaystyle m=\tan(\theta )}
    そして
    θ=arctan⁡(m){\displaystyle \theta =\arctan(m)}   （これは正接の逆関数です。逆三角関数を参照してください）。

例

例えば、点(2,8)と点(3,20)を通る直線を考えてみましょう。この直線の傾きmは

(20−8)(3−2)=12.{\displaystyle {\frac {(20-8)}{(3-2)}}=12.}

次に、点と傾きの形式で直線の方程式を書きます。

y−8=12(x−2)=12x−24.{\displaystyle y-8=12(x-2)=12x-24.}

または

y=12x−16.{\displaystyle y=12x-16.}

この直線がx軸となす-90°と90°の間の角度θは

θ=arctan⁡(12)≈85.2∘.{\displaystyle \theta =\arctan(12)\approx 85.2^{\circ }.}

2本の直線y = −3 x + 1とy = −3 x − 2を考えてみましょう。どちらの直線も傾きはm = −3です。これらは同じ直線ではありません。つまり、平行線です。

2つの直線 y = −3 x + 1とy = ⁠を考えます。x/3⁠ − 2。最初の直線の傾きはm 1 = −3です。2番目の直線の傾きはm 2 = ⁠です1/3⁠これら2つの傾きの積は-1です。したがって、これら2つの直線は垂直です

統計

統計学では、与えられたデータサンプルに対する最小二乗回帰の最も適合する直線の勾配は、次のように表されます

m=rsysx{\displaystyle m={\frac {rs_{y}}{s_{x}}}}、

この量mは直線の回帰傾きと呼ばれます。量はピアソンの相関係数、はy値の標準偏差、はx値の標準偏差です。これは共分散比としても表すことができます。[ 6 ]y=mx+c{\displaystyle y=mx+c}r{\displaystyle r}sy{\displaystyle s_{y}}sx{\displaystyle s_{x}}

m=cov⁡(Y,X)cov⁡(X,X){\displaystyle m={\frac {\operatorname {cov} (Y,X)}{\operatorname {cov} (X,X)}}}

微積分

各点における導関数は、その点で曲線に接する直線の傾きです。注：点Aにおける導関数は、緑色の二点鎖線では正、赤色の破線では負、黒色の実線では0です

傾きの概念は微分積分学の中心的な概念です。非線形関数の場合、変化率は曲線に沿って変化します。ある点における関数の微分は、その点における曲線の接線の傾きであり、したがって、その点における関数の変化率に等しくなります。

曲線上の2点間の 距離をΔ xとΔ yとすると（それぞれx軸とy軸に沿った距離）、上記の定義で与えられる傾きは、

m=ΔyΔx{\displaystyle m={\frac {\Delta y}{\Delta x}}}、

曲線に対する割線の傾きです。直線の場合、任意の2点間の割線は直線自体となりますが、他の種類の曲線ではそうではありません。

たとえば、y = x 2と交差する正割線の傾きは (0,0) と (3,9) で 3 です。 ( x = 3 ⁄ 2における接線の傾きも 3 − 平均値定理の結果です。)

Δ yと Δ x が減少するように 2 点を近づけると、割線は曲線の接線に近づき、その結果、割線の傾きは接線の傾きに近づきます。微分積分を使用すると、極限、つまり Δ yとΔ xが0に近づくにつれてΔ y /Δ xが近づく値を決定できます。したがって、この極限は接線の正確な傾きになります。yがxに依存する場合は、 Δ xのみが 0 に近づく極限を取れば十分です。したがって、接線の傾きは、 Δ xが 0 に近づくにつれてΔ y /Δ xの極限、つまり d y /d xです。この極限を導関数と呼びます。

dydx=limΔx→0ΔyΔx{\displaystyle {\frac {\mathrm {d} y}{\mathrm {d} x}}=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}}

関数上の特定の点における導関数の値は、その正確な位置における接線の傾きを与えます。例えば、y = x 2とします。この関数上の点は (−2,4) です。この関数の導関数はd y ⁄ d x = 2 xです。したがって、 (−2,4) におけるyの接線の傾きは2 ⋅ (−2) = −4です。この接線の方程式は、y − 4 = (−4)( x − (−2))またはy = −4 x − 4です。

傾きの差

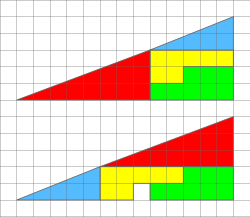
青い三角形と赤い三角形が交わる部分の傾きを比較すると、面積のパラドックスの錯覚は払拭されます

角度の概念の拡張は、傾斜の差から導き出されます。せん断写像を考えてみましょう。

(u,v)=(x,y)(1v01).{\displaystyle (u,v)=(x,y){\begin{pmatrix}1&v\\0&1\end{pmatrix}}.}

はに写像されます。 の傾きは0で、 の傾きはです。せん断写像により の傾きが追加されました。 上の2点が傾き と である場合、画像 (1,0){\displaystyle (1,0)}(1,v){\displaystyle (1,v)}(1,0){\displaystyle (1,0)}(1,v){\displaystyle (1,v)}v{\displaystyle v}v{\displaystyle v}{(1,y):y∈R}{\displaystyle \{(1,y):y\in \mathbb {R} \}}m{\displaystyle m}n{\displaystyle n}

(1,y)(1v01)=(1,y+v){\displaystyle (1,y){\begin{pmatrix}1&v\\0&1\end{pmatrix}}=(1,y+v)}

の傾きは だけ増加しますが、傾きの差はせん断の前後で同じです。この傾き差の不変性により、傾きは角度不変測度となり、円角（回転に対して不変）や双曲角と同等であり、スクイーズ写像の不変群 を持ちます。[ 7 ] [ 8 ]v{\displaystyle v}n−m{\displaystyle n-m}

屋根の傾斜

屋根の勾配は、伝統的に一般的に屋根勾配と呼ばれ、アメリカの大工や建築業界では、イギリス帝国単位系に由来する1フィートの整数分数（幾何正接、高さ÷長さ）で表されます。他の地域では、同様の慣習に基づき、他の単位が使用されています。詳細については、屋根勾配を参照してください。

道路や鉄道の勾配

道路や鉄道の勾配を表す一般的な方法は2つあります。1つは0°から90°までの角度（度）で表す方法で、もう1つは勾配をパーセンテージで表す方法です。「急勾配鉄道」と「ラック式鉄道」も参照してください。

パーセンテージで表された傾斜を度単位の角度に変換したり、その逆を行ったりする式は次のとおりです。

angle=arctan⁡(slope100%){\displaystyle {\text{angle}}=\arctan \left({\frac {\text{slope}}{100\%}}\right)}（これは正接の逆関数です。三角法を参照してください）

そして

slope=100%×tan⁡(angle),{\displaystyle {\mbox{slope}}=100\%\times \tan({\mbox{angle}}),}

ここで角度は度単位で、三角関数は度単位で動作します。例えば、傾斜が100 %または1000 ‰の場合、角度は45°です

3つ目の方法は、1単位の勾配を10、20、50、または100の水平単位で表す方法です（例：1:10）。1:20、1:50、または1:100（または「1/10」、「1/20」など）は、1:10の方が1:20よりも急勾配です。例えば、勾配が20%の場合、勾配は1:5、つまり11.3°の傾斜となります。

道路や鉄道には縦断勾配と横断勾配があります。

その他の用途

傾きや勾配の概念は、数学における他の応用を開発するための基礎としても使用されます

  • 勾配降下法は、関数の最小値を見つけるための一次反復最適化アルゴリズムです。
  • 勾配定理、勾配場を通る線積分は、曲線の端点で元のスカラー場を評価することによって評価できるという定理
  • 勾配法、現在の点における関数の勾配によって定義される探索方向を持つ問題を解くアルゴリズム
  • 共役勾配法、特定の線形方程式系の数値解法アルゴリズム
  • 非線形共役勾配法は、共役勾配法を非線形最適化に一般化します。
  • 確率的勾配降下法、微分可能な目的関数を最適化するための反復法

参照

参考文献

  1. ^ Clapham, C.; Nicholson, J. (2009). 「Oxford Concise Dictionary of Mathematics, Gradient」(PDF) . Addison-Wesley. p. 348. 2013年10月29日時点のオリジナル(PDF)からアーカイブ。2013年9月1日閲覧
  2. ^オブライエン、M.（1844）、平面座標幾何学に関する論文、または平面幾何学の問題の解決における座標法の応用、ケンブリッジ、イギリス：デイトンズ
  3. ^トッドハンター、I.（1888）、直線と円錐断面に応用された平面座標幾何学に関する論文、ロンドン：マクミラン
  4. ^ Weisstein, Eric W. 「Slope」 . MathWorld--A Wolfram Web Resource. 2016年12月6日時点のオリジナルよりアーカイブ。2016年10月30日閲覧。
  5. ^この慣例の初期の例としては、Salmon, George (1850). A Treatise on Conic Sections (2nd ed.). Dublin: Hodges and Smith. pp.  14– 15が挙げられます。
  6. ^ Further Mathematics Units 3&4 VCE（改訂版） . Cambridge Senior Mathematics. 2016. ISBN 9781316616222– 物理コピー経由
  7. ^ボルト、マイケル、フェルディナンズ、ティモシー、カヴリー、ランドン (2009). 「放物線を放物線に写像する最も一般的な平面変換」 . Involve: A Journal of Mathematics . 2 (1): 79– 88. doi : 10.2140/involve.2009.2.79 . ISSN 1944-4176 . 2020年6月12日時点のオリジナルよりアーカイブ。2021年5月22日閲覧 
  8. ^抽象代数/せん断と傾斜（Wikibooks）
無料辞書『ウィクショナリー』で「上り坂」を調べてください
「 https://en.wikipedia.org/w/index.php?title=Slope&oldid=1334362344」から取得