錯体の安定度定数

錯体化学において、安定度定数（生成定数または結合定数とも呼ばれる）は、溶液中での錯体形成における平衡定数である。これは、錯体を形成する試薬間の相互作用の強さの尺度である。錯体には主に2種類ある。金属イオンと配位子の相互作用によって形成される化合物と、ホスト-ゲスト錯体やアニオン錯体などの超分子錯体である。安定度定数は、溶液中の錯体の濃度を計算するために必要な情報を提供する。化学、生物学、医学など、多くの分野に応用されている。

歴史

ヤニック・ビェルム（ニールス・ビェルムの息子）は1941年に、金属アミン錯体の安定度定数を決定するための最初の一般的な方法を開発した。^{[ 1 ]}なぜこの方法が、アルフレッド・ヴェルナーが配位錯体の正しい構造を提唱してから約50年後という遅い時期に開発されたのかは、ベックとナジパルによってまとめられている。^{[ 2 ]}ビェルムの方法の鍵は、当時開発されたばかりのガラス電極とpHメーターを用いて溶液中の水素イオン濃度を測定したことである。ビェルムは、配位子と金属錯体との形成は一種の酸塩基平衡であることを認識していた。つまり、配位子Lをめぐって金属イオンM ⁿ⁺と水素イオンH ⁺が競合する。これは、同時に存在する2つの平衡を考慮しなければならないことを意味する。以下では、一般性のために電荷は省略する。2つの平衡とは、

${\displaystyle \mathrm {H+L} \leftrightharpoons \mathrm {HL} }$

${\displaystyle \mathrm {M+L} \leftrightharpoons \mathrm {ML} }$

したがって、MとHLの混合物を塩基で滴定する際の水素イオン濃度を追跡し、 HLの酸解離定数を知ることで、MLの形成に関する安定度定数を決定することができる。ビェルムはさらに、多くの錯体が形成される可能性のある系の安定度定数を決定した。

${\displaystyle \mathrm {M} +q\mathrm {L} \leftrightharpoons \mathrm {ML} _{q}}$

その後の20年間で、決定された安定度定数の数は爆発的に増加しました。アーヴィング・ウィリアムズ級数などの関係式が発見されました。計算はいわゆるグラフィカル法を用いて手作業で行われました。この時期に使用された手法の基礎となる数学は、ロッソッティとロッソッティによって要約されています。^{[ 3 ]}次の重要な進歩は、計算にコンピュータプログラムLETAGROP ^{[ 4 ] [ 5 ]}の使用でした。これにより、手計算では評価できないほど複雑な系の解析が可能になりました。その後、SCOGS ^{[ 6 ]}やMINIQUAD ^{[ 7 ]}といった、一般的な複雑な平衡状態を扱うことができるコンピュータプログラムが開発され、今日では安定度定数の決定はほぼ「日常的な」作業となっています。数千もの安定度定数の値は、2つの商用データベースで見つけることができます。^{[ 8 ] [ 9 ]}

理論

金属イオンMと配位子Lとの錯体形成は、実際には通常、置換反応です。例えば、水溶液中では金属イオンはアクアイオンとして存在するため、最初の錯体形成反応は次のように表すことができます 。

${\displaystyle \mathrm {[M(H_{2}O)} _{n}]+\mathrm {L} \leftrightharpoons \mathrm {[M(H_{2}O)} _{n-1}\mathrm {L} ]+\mathrm {H_{2}O} }$

この反応の平衡定数は次のように与え られる。

${\displaystyle \beta ^{'}={\frac {[\mathrm {M(H_{2}O)} _{n-1}\mathrm {L} ][\mathrm {H_{2}O} ]}{[\mathrm {M(H_{2}O)} _{n}][\mathrm {L} ]}}}$

[L]は「Lの濃度」と読み替え、角括弧内の他の項も同様です。定数項を省くことで、式は大幅に簡略化されます。各金属イオンに結合している水分子の数は一定です。希薄溶液では、水の濃度は実質的に一定です。式は次のようになります。

${\displaystyle \beta =\mathrm {\frac {[ML]}{[M][L]}} .}$

この単純化に従って、一般均衡に対する一般的な定義を与えることができる。

${\displaystyle p\mathrm {M} +q\mathrm {L} \leftrightharpoons \mathrm {M} _{p}\mathrm {L} _{q}}$

${\displaystyle \beta _{pq...}={\frac {[\mathrm {M} _{p}\mathrm {L} _{q}...]}{[\mathrm {M} ]^{p}[\mathrm {L} ]^{q}...}}}$

この定義は、任意の数の試薬を含むように容易に拡張できます。試薬は必ずしも金属と配位子である必要はなく、錯体を形成する任意の種とすることができます。このように定義された安定度定数は会合定数です。pK a値は解離定数であるため_、混乱を招く可能性があります。汎用コンピュータプログラムでは、すべての定数を会合定数として定義するのが慣例です。この2種類の定数の関係は、会合定数と解離定数に示されています。

段階的定数と累積定数

累積定数または全体定数（記号βで表す）は、試薬から錯体を形成する際の定数である。例えば、ML ₂の形成における累積定数は次のように表される。

${\displaystyle {\ce {{M}+ 2L <=> ML2}}}$ ;     ${\displaystyle \beta _{1,2}=\mathrm {\frac {[ML_{2}]}{[M][L]^{2}}} }$

段階的定数K ₁およびK _{2 は}、複合体が 1 段階ずつ形成されることを表します。

${\displaystyle {\ce {{M}+ L <=> ML}}}$ ;     ${\displaystyle K_{1}=\mathrm {\frac {[ML]}{[M][L]}} }$

${\displaystyle {\ce {{ML}+ L <=> ML2}}}$ ;     ${\displaystyle K_{2}=\mathrm {\frac {[ML_{2}]}{[ML][L]}} }$

すると、

${\displaystyle \beta _{1,2}=K_{1}K_{2}\,}$

累積定数は常に段階的定数の積として表すことができます。逆に、段階的定数は2つ以上の全体定数の商として表すことができます。段階的定数には統一された表記法はありませんが、Kのような記号が用いられます。^L _ML文献には時々記載されています。上記のように、各安定定数を明示的に指定することをお勧めします。

加水分解生成物

ヒドロキソ錯体の形成は加水分解反応の典型的な例です。加水分解反応とは、基質が水と反応し、水分子を水酸化物イオンと水素イオンに分解する反応です。この場合、水酸化物イオンは基質と錯体を形成します。

${\displaystyle \mathrm {M+OH} \leftrightharpoons \mathrm {M(OH)} }$ ;    ${\displaystyle K=\mathrm {\frac {[M(OH)]}{[M][OH]}} }$

水中では、水酸化物の濃度は自己イオン化定数K _wによって水素イオンの濃度と関連しています。

${\displaystyle K_{w}=\mathrm {[H]} ^{+}\mathrm {[OH]} ^{-}}$

水酸化物濃度の式を生成定数の式に代入する。

${\displaystyle K={\frac {[\mathrm {M} (\mathrm {OH} )]}{[\mathrm {M} ]K_{\mathrm {w} }[\mathrm {H} ]^{-1}}}}$

${\displaystyle \beta _{1,-1}^{*}=KK_{\mathrm {w} }={\frac {[\mathrm {M} (\mathrm {OH} )]}{[\mathrm {M} ][\mathrm {H} ]^{-1}}}}$

一般的に、反応については

${\displaystyle \mathrm {M} +n\mathrm {OH} \leftrightharpoons \mathrm {M(OH} )_{n}}$     ${\displaystyle \log \beta _{1,-n}^{*}\approx \log K-14n}$

古い文献では、加水分解定数としてlog Kの値が引用されることが多い。また、一般化学式M _p L _q (OH) _{rで表される加水分解錯体については、log} β ^*値が引用されることが多い。

酸塩基錯体

ルイス酸A とルイス塩基B は複合体 AB を形成すると考えられます。

${\displaystyle {\ce {A + B <=> AB,}}}$     ${\displaystyle K={\frac {{\ce {[AB]}}}{{\ce {[A][B]}}}}$

ルイス酸と塩基の強さとそれらの相互作用に関しては、主に 3 つの理論があります。

1. ハード酸塩基理論とソフト酸塩基理論（HSAB）。^{[ 10 ]}これは主に定性的な目的で使用されます。
2. ドラゴとウェイランドは、非常に多くの付加物の標準生成エンタルピーを非常に正確に予測する2パラメータ方程式を提案した。−Δ H ^⊖ (A − B) = E _A E _B + C _A C _B。EパラメータとCパラメータの値は入手可能である。^{[ 11 ]}
3. グットマンドナー数：塩基の場合、溶媒として1,2-ジクロロエタンを用いた場合の塩基と五塩化アンチモンの反応エンタルピーから算出される。酸の場合、アクセプター数は酸とトリフェニルホスフィンオキシドの反応エンタルピーから算出される。^{[ 12 ]}

熱力学

金属イオン錯体形成の熱力学は、多くの重要な情報を提供します。^{[ 13 ]}特に、エンタルピー効果とエントロピー効果を区別するのに役立ちます。エンタルピー効果は結合強度に依存し、エントロピー効果は溶液全体の秩序／無秩序の変化に関係しています。以下に示すキレート効果は、熱力学の観点から最もよく説明されます。

平衡定数は、反応の 標準ギブス自由エネルギー変化と関係している。

${\displaystyle \Delta G^{\ominus }=-2.303RT\log \beta }$

Rは気体定数、Tは絶対温度です。25℃では、Δ G ^⊖ = (−5.708 kJ mol ⁻¹ ) ⋅ log βとなります。自由エネルギーはエンタルピー項とエントロピー項から構成されます。

${\displaystyle \Delta G^{\ominus }=\Delta H^{\ominus }-T\Delta S^{\ominus }}$

標準エンタルピー変化は、熱量測定法またはファントホッフの式を用いて決定できますが、熱量測定法の方が好ましいです。標準エンタルピー変化と安定度定数が両方決定されていれば、上記の式から標準エントロピー変化は容易に計算できます。

_{ML n}型錯体の段階的形成定数がnの増加に伴って減少するという事実は、エントロピー因子によって部分的に説明できるかもしれない。八面体錯体の形成を例に挙げてみよう。

${\displaystyle {\ce {{M(H2O)_{\mathit {m}}L_{{\mathit {n}}-1}}+L<=>M(H2O)_{{\mathit {m}}-1}L_{\mathit {n}}}}$

最初のステップでは、m = 6、n = 1であり、リガンドは6つのサイトのうちの1つに入ることができます。2番目のステップでは、m = 5であり、2番目のリガンドは5つのサイトのうちの1つしか入ることができません。これは、最初のステップの方が2番目のステップよりもランダム性が高いことを意味します。Δ S ^⊖はより正であるため、Δ G ^⊖はより負になり、 。ステップごとの安定度定数の比はこれに基づいて計算できますが、Δ H ^{⊖ は}各ステップで必ずしも同じではないため、実験的な比はまったく同じではありません。^{[ 14 ]}この規則の例外については、以下の#キレート効果と#幾何学的因子で説明します。 ${\displaystyle K_{1}>K_{2}}$

イオン強度依存性

熱力学的平衡定数K⊖^は、平衡

${\displaystyle {\ce {M + L <=> ML}}}$

次のように 定義できる^{[ 15 ]}

${\displaystyle K^{\ominus }={\frac {{\ce {\{ML\}}}}{{\ce {\{M\}\{L\}}}}}$

ここで、{ML}は化学種MLの活量などです。活量は無次元であるため、 K⊖^も無次元です。生成物の活量は分子に、反応物の活量は分母に置きます。この式の導出については、 活量係数を参照してください。

活性は濃度と活性係数（γ ）の積であるため、定義は次のようにも書ける。

${\displaystyle K^{\ominus }={\frac {{\ce {[ML]}}}{{\ce {[M][L]}}}\times {\frac {\gamma _{{\ce {ML}}}}{\gamma _{{\ce {M}}}\gamma _{{\ce {L}}}}={\frac {{\ce {[ML]}}}{{\ce {[M][L]}}}\times \Gamma }$

ここで、[ML]はMLの濃度、Γは活量係数の商である。この式は次のように一般化できる。

${\displaystyle \beta _{pq...}^{\ominus }={\frac {[{\ce {M}}_{p}{\ce {L}}_{q}...]}{[{\ce {M}}]^{p}[{\ce {L}}]^{q}...}}\times \Gamma }$

^{[Cu(グリシン)] +}の生成安定度定数のイオン強度（NaClO ₄）依存性^{[ 16 ]}

活性度を用いる際の複雑さを避けるため、安定度定数は、可能な限り、高イオン強度の背景電解質溶液からなる媒体、すなわちΓが常に一定であると仮定できる条件下で決定される。 ^{[ 15 ]}例えば、媒体は0.1 mol dm ^−3の硝酸ナトリウム溶液、または3 mol dm ^−3の過塩素酸ナトリウム溶液である。Γが一定の場合、 Γは無視することができ、上記の理論上の一般式が得られる。

発表されている安定度定数の値はすべて、その決定に使用された特定のイオン媒体を参照し、錯体 CuL (L =グリシン酸塩) で示されているように、条件が異なると異なる値が得られます。さらに、同じイオン強度であっても電解質が異なればΓの値が異なるため、安定度定数の値は使用される特定の電解質に依存します。平衡状態にある種と背景電解質との間に化学相互作用がある必要はありませんが、特定のケースではそのような相互作用が発生する可能性があります。たとえば、リン酸塩はアルカリ金属と弱い錯体を形成するため、 ATPなどのリン酸塩を含む安定度定数を決定する場合、使用される背景電解質は、たとえばテトラアルキルアンモニウム塩になります。別の例としては、ハロゲン化物イオンやその他の陰イオンと弱い錯体を形成するが、過塩素酸イオン とは形成しない鉄 (III) があります。

公表されている定数が特定の用途に必要なイオン強度以外のイオン強度を示す場合、その定数は特異イオン理論（SIT）やその他の理論によって調整されることがある。^{[ 17 ]}

温度依存性

すべての平衡定数はファントホッフの式に従って温度とともに変化する^{[ 18 ]}

${\displaystyle {\frac {d(\ln K)}{dT}}={\frac {\Delta {\mathit {H}}_{\mathrm {m} }^{\ominus }}{RT^{2}}}}$

あるいは

${\displaystyle {\frac {d\ln K}{d(1/T)}}=-{\frac {\Delta H^{\ominus }}{R}}}$

Rは気体定数、Tは熱力学温度です。したがって、標準エンタルピー変化ΔH⊖が負となる発熱反応で^はKは温度とともに減少しますが、ΔH⊖^が正となる吸熱反応ではKは温度とともに増加します。

複合体の安定度定数に影響を与える要因

キレート効果

メチルアミン（左）およびエチレンジアミン（右）とのCu ^2+錯体

水溶液中における銅(II)イオンCu ²⁺とエチレンジアミン(en)とメチルアミンMeNH ₂との間の2つの平衡を考えてみましょう。

${\displaystyle {\ce {Cu^2+ + en <=> [Cu(en)]^2+}}}$

${\displaystyle {\ce {Cu^2+ + 2 MeNH2 <=> [Cu(MeNH2)2]^2+}}}$

最初の反応では、二座配位子のエチレンジアミンが銅イオンとキレート錯体を形成します。キレート化の結果、五員環が形成されます。2 番目の反応では、二座配位子がほぼ同じ供与力を持つ 2 つの単座メチルアミン配位子に置き換えられます。つまり、 2 つの反応における Cu–N 結合の生成エンタルピーはほぼ同じです。銅濃度が等しく、メチルアミンの濃度がエチレンジアミンの濃度の 2 倍の条件下では、二座錯体の濃度は 2 つの単座配位子を持つ錯体の濃度よりも高くなります。この効果はキレート環の数とともに増加するため、 5 つのキレート環を持つEDTA錯体の濃度は、2 つの単座窒素供与配位子と 4 つの単座カルボキシレート配位子を持つ対応する錯体よりもはるかに高くなります。したがって、キレート効果の現象はしっかりと確立された経験的事実です。同等の条件下では、キレート錯体の濃度は、単座配位子を持つ類似の錯体の濃度よりも高くなります。

キレート効果を説明するための熱力学的アプローチでは、反応の平衡定数を考慮します。平衡定数が大きいほど、複合体の濃度が高くなります。

${\displaystyle [{\ce {Cu(en)}}]=\beta _{11}{\ce {[Cu][en]}}}$

${\displaystyle [{\ce {Cu(MeNH2)2}}]=\beta _{12}{\ce {[Cu][MeNH2]^2}}}$

メチルアミンの分析濃度がエチレンジアミンの2倍で、銅の濃度が両方の反応で同じ場合、β 11 ≫ β 12 であるため、[Cu(en)] 2+ の濃度は_[  Cu  ( _MeNH 2 ) ² _] 2+_の濃度^よりもはるかに高くなります。

2つの安定度定数の差は、主に標準エントロピー変化ΔS⊖の差によるものである。^キレート配位子との反応では、左側に2つの粒子、右側に1つの粒子が存在するが、単座配位子との反応式では、左側に3つの粒子、右側に1つの粒子が存在する。これは、キレート錯体が形成される場合、単座配位子との錯体が形成される場合よりも、無秩序性のエントロピー損失が少ないことを意味する。これがエントロピー差に寄与する要因の1つである。その他の要因としては、溶媒和変化や環形成などが挙げられる。この効果を示す実験データを次の表に示す。^{[ 19 ]}

平衡	対数 β	Δ G ^⊖ /kJ モル^−1	Δ H ^⊖ /kJ モル^−1	− T Δ S ^⊖ /kJ モル^−1
Cd ^2+ + 4 MeNH 2 ⇌ Cd(MeNH2）^2+4	6.55	−37.4	−57.3	19.9
Cd ^2+ + 2 en ⇌ Cd(en)^2+2	10.62	−60.67	−56.48	−4.19

EDTA複合体

これらのデータは、2つの反応における標準エンタルピー変化が実際にほぼ等しいこと、そしてキレート錯体の方がはるかに安定である主な理由は、標準エントロピー項がそれほど不利ではないこと、実際この場合には有利であることを示している。一般に、分子レベルでの溶液の変化という観点から熱力学値を正確に説明することは困難であるが、キレート効果は主にエントロピーの影響であることは明らかである。シュワルツェンバッハ^{[ 20 ]による説明を含む他の説明については、グリーンウッドとアーンショー[ 19 ]}で議論されている。

ジエチレントリアミン

キレート環の数が増えるほど、キレート効果は増大します。たとえば、錯体 [Ni(dien) ₂ )] ²⁺は錯体 [Ni(en) ₃ )] ²⁺よりも安定しています。両方の錯体ともニッケルイオンの周りに 6 つの窒素原子を持つ八面体ですが、ジエン (ジエチレントリアミン、1,4,7-トリアザヘプタン) は三座配位子で、エンは二座配位子です。キレート環の数は、配位子のドナー原子の数より 1 つ少ないです。EDTA (エチレンジアミン四酢酸)は6 つのドナー原子を持つため、5 つのキレート環を持つ非常に強力な錯体を形成します。8 つのドナー原子を持つDTPAなどの配位子は、通常 8 または 9 配位錯体を形成するランタニドイオンやアクチニドイオンなどの大きな金属イオンとの錯体を形成するために使用されます。 5員環および6員環のキレート環は最も安定な錯体を形成します。4員環は環の結合角が小さいため、内部歪みを受けます。7員環および8員環では、より大きな環は剛性が低く、形成時に失われるエントロピーが少なくなるため、キレート効果も減少します。

脂肪族-OH基の脱プロトン化

2-アミノエタノール

トリス

水溶液中では、脂肪族-OH基からプロトンを除去することは困難です。これは、このプロセスに必要なエネルギーがかなり大きいためです。そのため、水溶液中での脂肪族-OH基のイオン化は、特殊な状況下でのみ起こります。そのような状況の一つとして、H ₂ N–C–C–OH構造を含む化合物が挙げられます。例えば、2-アミノエタノール構造を含む化合物は、脱プロトン化されたH ₂ N–C–C–O ⁻と金属キレート錯体を形成できます。このキレート効果により、O–H結合を切断するために必要な余分なエネルギーが供給されます。

重要な例として、トリス分子が挙げられます。この分子は、Fe ³⁺やCu ²⁺などのイオンとキレート錯体を形成するため、緩衝剤としては注意して使用する必要があります。

マクロサイクリック効果

銅(II)とマクロ環状配位子シクラム（1,4,8,11-テトラアザシクロテトラデカン）との錯体の安定性は、対応する開鎖アミンとの錯体の安定性と比較して、予想よりもはるかに高いことがわかった。^{[ 21 ]}この現象はマクロ環状効果 と名付けられ、エントロピー効果としても解釈された。しかし、その後の研究では、エンタルピーとエントロピーの両方の要因が関与していることが示唆された。^{[ 22 ]}

大環状配位子と開鎖（キレート）配位子の重要な違いは、錯体形成時に金属イオンが挿入される空洞の大きさに基づいて、金属イオンに対する選択性を持つ点である。例えば、クラウンエーテル18-クラウン-6は、より小さなナトリウムイオンNa ^+よりもカリウムイオンK ⁺とはるかに強力な錯体を形成する。^{[ 23 ]}

ヘモグロビンでは、鉄(II)イオンが大環状ポルフィリン環と錯体を形成しています。記事「ヘモグロビン」では、オキシヘモグロビンに鉄(III)が含まれていると誤って記載されています。現在では、ヘモグロビンの鉄(II )は低スピン錯体であるのに対し、オキシヘモグロビンでは高スピン錯体であることが分かっています。低スピンのFe ²⁺イオンはポルフィリン環の空洞にぴったり収まりますが、高スピンの鉄(II)はかなり大きく、鉄原子は大環状リガンドの平面から押し出されます。^{[ 24 ]}この効果により、ヘモグロビンは生物学的条件下で酸素を可逆的に結合することができます。ビタミンB12では、コバルト(II)イオンがコリン環に保持されています。クロロフィルはマグネシウム(II)の大環状錯体です。

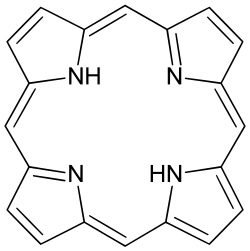サイクラム	最も単純なポルフィリンであるポルフィン。

一般的なクラウンエーテルの構造：12-クラウン-4、15-クラウン-5、18-クラウン-6、ジベンゾ-18-クラウン-6、およびアザクラウンエーテル

幾何学的要因

_{ML n}（n = 1, 2, ...）のような系列における段階的な生成定数K _{n は}、通常、 nが増加するにつれて減少します。この規則の例外は、ML _n錯体の形状が系列内のすべてのメンバーで同じではない場合に発生します。典型的な例は、水溶液中での ジアミン銀(I)錯体[Ag(NH ₃ ) ₂ ] ⁺の形成です。

${\displaystyle {\ce {Ag+ + NH3 <=> [Ag(NH_3)]^+}};\ K_{1}={\frac {{\ce {[Ag(NH3)]}}}{{\ce {[Ag][NH3]}}}}}$

${\displaystyle {\ce {Ag(NH3)+ + NH3 <=> [Ag(NH3)2]^+}};\ K_{2}={\frac {{\ce {[Ag(NH3)2]}}}{{\ce {[Ag(NH3)][NH3]}}}}}$

この場合、K ₂ > K _{1 で}ある。その理由は、水溶液中では、 Ag ⁺と書かれたイオンが実際には四配位四面体アクア種 [Ag(H ₂ O) ₄ ] ⁺として存在するためである。最初のステップは、結合した水分子をアンモニアが置換して四面体錯体 [Ag(NH ₃ )(H ₂ O) ₃ ] ⁺を形成する置換反応である。第2段階では、すべてのアクア配位子が失われ、線状の二配位生成物 [H ₃ N–Ag–NH ₃ ] ⁺が形成される。熱力学データ^{[ 25 ]}を調べると、エントロピー変化の差が、2つの錯形成反応の安定度定数の差の主な要因であることがわかっている。

平衡	Δ H ^⊖ /kJ モル^−1	Δ S ^⊖ /J K ^−1 モル^−1
Ag ^+ + NH 3 ⇌ [Ag(NH 3 )] ^+	−21.4	8.66
[Ag(NH 3 )] ^+ + NH 3 ⇌ [Ag(NH 3 ) 2 ] ^+	−35.2	−61.26

他には、[Co(H ₂ O) ₆ ] ^{2+から [CoCl} ₄ ] ²⁻が形成される場合のように、八面体から四面体への変化の例もある。

金属イオンの分類

Ahrland、Chatt、Davies は、金属イオンが、窒素、酸素、フッ素を供与原子とする配位子と、リン、硫黄、塩素を供与原子とする配位子よりも強い錯体を形成する場合、クラス A と記述でき、その逆の場合、クラス B と記述できると提案しました。^{[ 26 ]}例えば、Ni ^{2+ は}ホスフィンよりもアミンと強い錯体を形成しますが、Pd ^{2+ はアミンよりもホスフィンと強い錯体を形成します。後に、Pearson は}硬い酸と柔らかい酸と塩基の理論(HSAB 理論) を提唱しました。^{[ 27 ]}この分類では、クラス A の金属は硬い酸であり、クラス B の金属は柔らかい酸です。銅 (I) などの一部のイオンは、境界線として分類されます。硬い酸は、柔らかい塩基よりも硬い塩基と強い錯体を形成します。 HSAB理論は有用ではあるが、半定量的なものに過ぎない。^{[ 28 ]}

金属イオンの硬度は酸化数の増加とともに増加します。この効果の一例として、Fe ^{2+ は}O供与性配位子よりもN供与性配位子とより強い錯体を形成する傾向がありますが、Fe ³⁺の場合はその逆です。

イオン半径の影響

アーヴィング・ウィリアムズ系列は、第一遷移系列の高スピン八面体二価金属イオンを指す。この系列は錯体の安定性を以下の順序で分類する。

マンガン < 鉄 < コバルト < ニッケル < 銅 > 亜鉛

この順序は多種多様なリガンドに当てはまることがわかった。^{[ 29 ]}この系列の説明には3つの流れがある。

1. イオン半径はMn ²⁺からZn ²⁺へと周期的に減少すると予想されます。これは通常の周期的な傾向であり、安定性の全体的な増加を説明するものです。
2. 結晶場安定化エネルギー（CFSE）は、マンガン(II)ではゼロからニッケル(II)では最大まで増加します。これにより、錯体はますます安定します。CFSEは亜鉛(II)ではゼロに戻ります。
3. 銅(II)のCFSEはニッケル(II)よりも小さいですが、八面体銅(II)錯体はヤーン・テラー効果の影響を受け、その結果、錯体の安定性が高まります。

イオン半径の影響のもう一つの例は、一連の三価ランタニドイオンに沿った特定の配位子との錯体の安定性が着実に増加することであり、これはよく知られているランタニド収縮の影響です。

アプリケーション

安定度定数値は、幅広い用途で利用されています。キレート療法は、輸血を受けたβ-サラセミア患者の鉄過剰症など、さまざまな金属関連疾患の治療に使用されています。理想的なリガンドは標的の金属イオンに結合し、他の金属イオンには結合しませんが、この程度の選択性を達成するのは非常に困難です。合成薬デフェリプロンは、2つの酸素供与原子を持つことで選択性を実現し、Mg ²⁺、Ca ²⁺、Zn ²⁺などの人体に存在する他の二価イオンよりもFe ^{3+に優先して結合します。Pb 2+}やCd ²⁺などのイオンによる中毒の治療は、これらが二価イオンであり選択性を達成するのがより難しいため、はるかに困難です。^{[ 30 ]}ウィルソン病における過剰な銅は、ペニシラミンまたはトリエチレンテトラミン（TETA）で除去できます。DTPA はプルトニウム中毒の治療薬として米国食品医薬品局により承認されています。

DTPAはMRI造影増強におけるガドリニウムの錯化剤としても用いられる。この場合、Gd ^{3+は非常に毒性が強いため、錯体は非常に強力であることが求められる。八座配位子の大きな安定度定数により、遊離Gd 3+}の濃度はほぼ無視できるほど小さく、毒性閾値をはるかに下回る。^{[ 31 ]}さらに、配位子はガドリニウムイオン上の9つの配位サイトのうち8つしか占有しない。9番目のサイトは周囲の液体と急速に交換する水分子によって占有されており、このメカニズムによって常磁性錯体が造影剤となる。

EDTAはほとんどの二価陽イオンと非常に強力な錯体を形成するため、様々な用途に用いられています。例えば、洗濯洗剤にはカルシウムイオンとマグネシウムイオンを封鎖することで軟水剤として作用することが多く含まれています。

大環状配位子の選択性は、イオン選択電極の構築の基礎として利用できます。例えば、天然に存在する大環状抗生物質バリノマイシンを利用したカリウム選択電極が利用可能です。

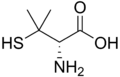デフェリプロン	ペニシラミン	トリエチレンテトラミン、TETA	エチレンジアミン四酢酸、EDTA
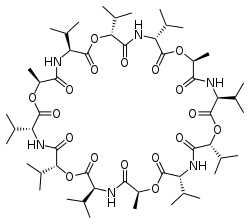ジエチレントリアミン五酢酸、DTPA	バリノマイシン	トリ-n-ブチルホスフェート

キレックス100などのイオン交換樹脂は、ポリマーに結合したキレート配位子を含み、軟水器やクロマトグラフィー分離技術に使用できます。溶媒抽出では、電気的に中性の錯体の形成により、陽イオンを有機溶媒に抽出できます。たとえば、核燃料の再処理では、ウラン(VI)とプルトニウム(VI)は錯体[MO ₂ (TBP) ₂ (NO ₃ ) ₂ ]（TBP =トリ-n-ブチルリン酸）として灯油に抽出されます。相間移動触媒では、有機溶媒に不溶性の物質を適切な配位子の添加によって可溶性にすることができます。たとえば、過マンガン酸カリウムの酸化は、水性反応混合物に触媒量のクラウンエーテルと少量の有機溶媒を添加して、酸化反応を有機相で起こさせることで達成できます。

これらの例すべてにおいて、配位子は形成される錯体の安定度定数に基づいて選択されます。例えば、TBPは（他の理由の中でも）溶媒抽出に十分な強度の錯体を形成しますが、硝酸によって分解されウラニルカチオンを[UO ₂ (NO ₃ ) ₄ ] ^2-などのニトラト錯体として水相に 戻すことができるほど弱い錯体を形成するため、核燃料再処理に使用されます。

超分子複合体

超分子複合体は、水素結合、疎水力、ファンデルワールス力、π-π相互作用、静電効果によって結合しており、これらはすべて非共有結合として説明できます。その用途としては、分子認識、ホスト-ゲスト化学、アニオンセンサーなどが挙げられます。

分子認識における典型的な応用例としては、三脚型置換尿素分子と様々な糖類との間で形成される複合体の形成定数の決定が挙げられる^{[ 32 ]}。この研究は、非水溶媒とNMR化学シフト測定を用いて行われた。その目的は、糖類に対する選択性を調べることであった。

化学センサーの開発における超分子複合体の利用例としては、ATPを感知するための遷移金属集団の利用が挙げられる。^{[ 33 ]}

アニオン錯体形成は、アニオンを適切なケージに封入することで達成できます。ケージの形状を設計することで、選択性を調整できます。例えば、ジカルボン酸アニオンは、2つの金属イオンを含む大きな大環状構造の楕円形の空洞に封入することができます。^{[ 34 ]}

実験方法

Bjerrum によって開発された方法は、測定精度が大幅に向上したにもかかわらず、現在でも主に使用されている方法です。最も一般的な方法は、高イオン強度の媒体中の金属イオンと配位子を含む溶液をまず酸性化し、配位子が完全にプロトン化されるようにします。次にこの溶液を、多くの場合コンピューター制御の自動滴定装置を使用して、CO ₂を含まない塩基溶液で滴定します。水素イオンの濃度、つまり活性は、ガラス電極を使用して監視します。計算に使用されるデータ セットは、存在する化学種の性質を定義するステートメント (システムのモデルと呼ばれる)、滴定に使用される試薬の濃度に関する詳細、最後に滴定と pH (または起電力)のペアの形式での実験測定値の 3 つの要素で構成されます。

他のイオン選択電極（ISE）も使用できます。例えば、フッ化物電極は、金属イオンのフッ素錯体の安定性の測定に使用できます。

ISEが常に使用できるとは限りません。その場合、他の測定方法で滴定をモニタリングできます。紫外可視分光法、蛍光分光法、NMR分光法が最も一般的に用いられる代替法です。現在では、様々な波長範囲で吸光度または蛍光を測定し、これらのデータを同時にフィッティングすることが一般的です。また、様々なNMR化学シフトも同時にフィッティング可能です。

化学モデルには、別の実験で決定された配位子のプロトン化定数、log  Kwの値_、および形成された錯体の未知の安定度定数の推定値が含まれます。これらの推定値は、計算に非線形最小二乗法アルゴリズムを使用するために必要です。推定値は通常、化学的に類似した系を参照して得られます。安定度定数データベース^{[ 8 ] [ 9 ]}は、関連する錯体の公開されている安定度定数を見つけるのに非常に役立ちます。

単純なケースでは、計算はスプレッドシートで行うことができます。^{[ 35 ]}それ以外の場合は、汎用コンピュータプログラムを用いて計算を行います。最もよく使用されるプログラムは以下のとおりです。

• 電位差測定および/または分光光度計によるデータ: PSEQUAD ^{[ 36 ]}
• 電位差測定データ: HYPERQUAD、^{[ 37 ]} BEST、^{[ 38 ]} ReactLab pH PRO
• 分光光度データ: HypSpec、SQUAD、^{[ 39 ]} SPECFIT、^{[ 40 ] [ 41 ]} ReactLab EQUILIBRIA、^{[ 42 ]}、suprafit ^{[ 43 ]}
• NMRデータHypNMR , ^{[ 44 ]} WINEQNMR2 Archived 2019-07-14 at the Wayback Machine ^{[ 45 ]} , suprafit ^{[ 46 ]}

生化学において、付加物の生成定数は等温滴定熱量測定（ITC）から得ることができます。この手法では、安定度定数と平衡の標準エンタルピー変化の両方が得られます。^{[ 47 ]}この手法は、ソフトウェアの可用性により、主に1:1の化学量論の錯体に限定されます。

批判的に評価されたデータ

以下の参考文献は、様々なクラスの配位子について発表された安定度定数に関する批評的なレビューです。これらのレビューはすべてIUPACによって出版されており、全文はPDF形式で無料で入手できます。

• エチレンジアミン（en）^{[ 48 ]}
• ニトリロ三酢酸（NTA）^{[ 49 ]}
• アミノポリカルボン酸（コンプレクソン）^{[ 50 ]}
• アルファヒドロキシ酸およびその他のヒドロキシカルボン酸^{[ 51 ] [ 52 ]}

• クラウンエーテル^{[ 53 ]}

• ホスホン酸^{[ 54 ] [ 55 ]}

• イミダゾールとヒスタミン^{[ 56 ]}

• 極性側鎖を持つアミノ酸^{[ 57 ]}

• ヌクレオチド^{[ 58 ]}

• アセチルアセトン^{[ 59 ]}

• 一般^{[ 60 ]}

• 無機配位子を用いた環境的に重要な重金属の化学種分析。パート1：Hg ²⁺ –Cl ⁻、OH ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​システム^{[ 61 ]}
• 無機配位子を用いた環境的に重要な金属の化学種分析 パート2：Cu ²⁺ –OH ⁻、Cl ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​水系^{[ 62 ]}
• 無機配位子を用いた環境的に重要な金属の化学種分析 パート3：Pb ²⁺ –OH ⁻、Cl ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​システム^{[ 63 ]}
• 無機配位子を用いた環境的に重要な金属の化学種分析。第4部：Cd ²⁺ –OH ⁻、Cl ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​システム^{[ 64 ]}

データベース

• Ki データベースは、受容体、神経伝達物質トランスポーター、イオンチャネル、酵素に対する薬物および化合物の結合親和性 (Ki) が公開されているパブリック ドメイン データベースです。
• BindingDBは、測定された結合親和性のパブリックドメインデータベースであり、主に薬物標的と考えられるタンパク質と小さな薬物様分子との相互作用に焦点を当てています。

参考文献

1. ビェラム、J. (1941)。水溶液中での金属アンミンの形成。コペンハーゲン：ハーセ。
2. Beck, MT; Nagypál, I. (1990). 「第1章」.複雑平衡の化学. Horwood. ISBN 0-85312-143-5。
3. Rossotti, FJC; Rossotti, H. (1961).安定度定数の決定. McGraw–Hill.
4. Dyrssen, D.; Ingri, N.; Sillen, LG (1961). 「ピットマッピング - 安定度定数のコンピュータによる精密化への一般的なアプローチ」 . Acta Chem. Scand . 15 : 694–696 . doi : 10.3891/acta.chem.scand.15-0694 .
5. イングリ、N. LG のシレン (1964 年)。 「グラフィカル手法の補足としての高速コンピュータ、IV. LETAGROP-VRID の ALGOL バージョン」。アルキフ・フォー・ケミ。23：97～ 121
6. Sayce, IG (1968). 「金属イオンと錯化試薬の混合物中に存在する種の平衡定数のコンピュータ計算」Talanta . 15 (12): 1397– 1421. doi : 10.1016/0039-9140(68)80200-0 . PMID 18960446 . 
7. Sabatini, A.; Vacca, A.; Gans, P. (1974). 「MINIQUAD - 安定定数の計算のための汎用コンピュータプログラム」. Talanta . 21 (1): 53– 77. doi : 10.1016/0039-9140(74)80063-9 . PMID 18961420 . 
8. IUPAC SCデータベース金属錯体および配位子の平衡定数に関する公開データの包括的なデータベース
9. NIST 標準参照データベース 46 NIST 厳選金属錯体の安定度定数: バージョン 8.0 (このデータベースは廃止されました。)
10. ピアソン, RG (1997). 『化学的硬度：分子から固体への応用』 Springer-VCH. ISBN 3-527-29482-1。
11. Drago, RS; Wong, N.; Bilgrien, C.; Vogel, C. (1987). 「ハメット置換基定数からのEおよびCパラメータと、 EおよびCを用いたコバルト–炭素結合エネルギーの理解」. Inorg. Chem . 26 (1): 9– 14. doi : 10.1021/ic00248a003 .
12. Gutmann, V. (1978).分子相互作用へのドナー・アクセプターアプローチ. Springer. ISBN 0-306-31064-3。
13. Rossotti, FJC (1960). 「溶液中における金属イオン錯体形成の熱力学」 Lewis, J.; RG, Wilkins (編).現代配位化学ニューヨーク: インターサイエンス.
14. Beck, MT; Nagypál, I. (1990).複雑平衡の化学. Horwood. ISBN 0-85312-143-5。セクション3.5.1.2、6.6.1、および6.6.2
15. Rossotti, FJC; Rossotti, H. (1961). 「第2章 活性と濃度指数」.安定度定数の決定. McGraw–Hill.
16. ゲルゲリー、A.;ナジパル、I。 E.、ファルカス (1974)。 「A réz(II)-aminosav törzskomplexek vizes oldatában lejátszodó protoncsere-reakciók kinetikájának NMR-vizsgalata」[銅(II)-アミノ酸親錯体の水溶液におけるプロトン交換プロセスの NMR 研究]。マジャール語 ケミアイ・フォリオラト。80 : 545–549 .
17. 「プロジェクト：イオン強度補正による安定度定数」IUPAC . 2008年10月29日時点のオリジナルよりアーカイブ。 2008年11月23日閲覧。
18. Atkins, PW; De Paula, J. (2006). 「セクション7.4：平衡の温度に対する応答」.物理化学. オックスフォード大学出版局. ISBN 0-19-870072-5。
19. グリーンウッド, ノーマン・N. ; アーンショウ, アラン (1997).元素化学（第2版）.バターワース・ハイネマン. doi : 10.1016/C2009-0-30414-6 . ISBN 978-0-08-037941-8。910ページ
20. Schwarzenbach、G. (1952)。 「Der Chelateffekt」[キレート効果]。ヘルブ。チム。アクタ。35 (7): 2344–2359。土井: 10.1002/hlca.19520350721。
21. Cabinness, DK; Margerum, DW (1969). 「銅(II)テトラミン錯体の安定性に対するマクロ環状化合物の効果」J. Am. Chem. Soc . 91 (23): 6540– 6541. Bibcode : 1969JAChS..91.6540C . doi : 10.1021/ja01051a091 .
22. Lindoy, LF (1990). 「第6章 熱力学的考察」.大環状配位子錯体の化学. ケンブリッジ大学出版局. ISBN 0-521-40985-3。
23. Pedersen, CJ (1967). 「環状ポリエーテルと金属塩との錯体」. J. Am. Chem. Soc . 89 (26): 7017– 7036. Bibcode : 1967JAChS..89.7017P . doi : 10.1021/ja01002a035 .
24. Greenwood, Norman N. ; Earnshaw, Alan (1997). Chemistry of the Elements (第2版). Butterworth-Heinemann . doi : 10.1016/C2009-0-30414-6 . ISBN 978-0-08-037941-8。1100ページ、図25.7
25. Lundeen, M.; Hugus, ZZ (1992). 「いくつかの金属イオン錯体形成平衡に関する熱量測定研究」Thermochim. Acta . 196 (1): 93– 103. Bibcode : 1992TcAc..196...93L . doi : 10.1016/0040-6031(92)85009-K .
26. Ahrland, S.; Chatt, J.; Davies, NR (1958). 「リガンド原子とアクセプター分子およびイオンの相対親和力」. Quart. Rev. 12 ( 3): 265– 276. doi : 10.1039/QR9581200265 .
27. Pearson, RG (1963). 「硬い酸と柔らかい酸、塩基」. J. Am. Chem. Soc . 85 (22): 3533– 3539. Bibcode : 1963JAChS..85.3533P . doi : 10.1021/ja00905a001 .
28. Beck, MT; Nagypál, I. (1990).複雑平衡の化学. Horwood. p. 354. ISBN 0-85312-143-5。
29. Irving, HMNH; Williams, RJP (1953). 「遷移金属錯体の安定性」. J. Chem. Soc. : 3192– 3210. doi : 10.1039/JR9530003192 .
30. Arena, G.; Contino, A.; Longo, E.; Sciotto, D.; Spoto, G. (2001). 「1,3-交互配座を有する新規アリル官能基化チオアミドカリックス[4]アレーンによる軟質Pb ²⁺およびHg ²⁺の選択的錯形成：UV-可視およびH-1 NMR分光法による検討」J. Chem. Soc., Perkin Trans . 2 (12): 2287– 2291. doi : 10.1039/b107025h .
31. Runge, VM; Scott, S. (1998).造影臨床磁気共鳴画像法. ケンタッキー大学出版局. ISBN 0-8131-1944-8。
32. Vacca, A.; Nativi, C.; Cacciarini, M.; Pergoli, R.; Roelens, S. (2004). 「単糖類の分子認識のための新たな三脚型受容体．1H NMR分光法によるグリコシド結合親和性と選択性評価のパラダイム^」．J . Am. Chem. Soc . 126 (50): 16456– 16465. Bibcode : 2004JAChS.12616456V . doi : 10.1021/ja045813s . PMID 15600348 . 
33. Marcotte, N.; Taglietti, A. (2003). 「遷移金属ベースの化学センシングアンサンブル：生理学的条件下でのATPセンシング」. Supramol. Chem . 15 (7): 617– 717. doi : 10.1080/10610270310001605205 ​​. S2CID 96018200 . 
34. Boiocchi, M.; Bonizzoni, M.; Fabbrizzi, L.; Piovani, G.; Taglietti, A. (2004). 「水中のジカルボン酸アニオンの蛍光検出のための長楕円体キャビティを備えた二金属ケージ」. Angew. Chem. Int. Ed . 43 (29): 3847– 3852. doi : 10.1002/anie.200460036 . PMID 15258953 . 
35. Billo, EJ (1997). 「第22章」 . Excel for Chemists: A comprehensive guide (第2版). Wiley-VCH. ISBN 0-471-18896-4。
36. Zekany, L.; Nagypál, I. (1985). 「第8章 PSEQUAD: 分析的微分を用いた電位差測定および/または分光光度測定の平衡データ評価のための包括的プログラム」Leggett (編).形成定数の決定のための計算法. Plenum. ISBN 0-306-41957-2。
37. Gans, P.; Sabatini, A.; Vacca, A. (1996). 「溶液中の平衡状態の調査．HYPERQUADプログラム群を用いた平衡定数の決定」. Talanta . 43 (10): 1739– 1753. doi : 10.1016/0039-9140(96)01958-3 . PMID 18966661 . 
38. Martell, AE; Motekaitis, RJ (1992).安定度定数の決定と利用. Wiley-VCH.
39. Leggett, D. (1985). 「第6章 SQUAD：吸光度データからの安定度商」. Leggett (編).形成定数の決定のための計算方法. Plenum. ISBN 0-306-41957-2。
40. Gampp, M.; Maeder, M.; Mayer, CJ; Zuberbühler, AD (1985). 「多波長分光データからの平衡定数の計算—I：数学的考察」. Talanta . 32 (2): 95– 101. doi : 10.1016/0039-9140(85)80035-7 . PMID 18963802 . 
41. Gampp, M.; Maeder, M.; Mayer, CJ; Zuberbühler, AD (1985). 「多波長分光データからの平衡定数の計算—II1: Specfit: BasicおよびStandard Fortran 77で書かれた2つのユーザーフレンドリーなプログラム」. Talanta . 32 (4): 251– 264. doi : 10.1016/0039-9140(85)80077-1 . PMID 18963840 . 
42. Jplusコンサルティング株式会社
43. C. Hübler, Chem. Methods 2022, e202200006. DOI 10.1002/cmtd.202200006
44. Frassineti, C.; Alderighi, L.; Gans, P.; Sabatini, A.; Vacca, A.; Ghelli, S. (2003). 「新しいコンピュータプログラムHypNMR2000で処理された¹³ C NMRデータによるいくつかのフッ素化ポリアミンのプロトン化定数の決定．ポリアミンにおけるプロトン化配列」. Anal. Bioanal. Chem . 376 (7): 1041– 1052. doi : 10.1007/s00216-003-2020-0 . hdl : 11380/306695 . PMID 12845401. S2CID 14533024 .  
45. Hynes, MJ (1993). 「EQNMR: 核磁気共鳴化学シフトデータから安定度定数を計算するコンピュータプログラム」J. Chem. Soc., Dalton Trans. (2): 311– 312. doi : 10.1039/DT9930000311 .
46. C. Hübler, Chem. Methods 2022, e202200006. DOI 10.1002/cmtd.202200006
47. O'Brien, R.; Ladbury, JE; Chowdry, BZ (2000). 「第10章」 Harding, SE; Chowdry, BZ (編).タンパク質-リガンド相互作用：流体力学と熱量測定. オックスフォード大学出版局. ISBN 0-19-963749-0。
48. Paoletti, P. (1984). 「エチレンジアミンによる金属錯体の形成：平衡定数、エンタルピー値、エントロピー値の批判的調査」(PDF) . Pure Appl. Chem . 56 (4): 491– 522. doi : 10.1351/pac198456040491 . S2CID 5600085 . 
49. Anderegg, G. (1982). 「NTA錯体の安定度定数に関する批判的調査」(PDF) . Pure Appl. Chem . 54 (12): 2693– 2758. doi : 10.1351/pac198254122693 . S2CID 44040841 . 
50. Anderegg, G; Arnaud-Neu, F.; Delgado, R.; Felcman, J.; Popov, K. (2003). 「バイオメディカルおよび環境用途におけるコンプレクソン類の金属錯体の安定度定数の批判的評価（IUPAC技術報告書）」(PDF) . Pure Appl. Chem . 77 (8): 1445–95 . doi : 10.1351/pac200577081445 . S2CID 94957415 . 
51. Lajunen, LHJ; Portanova, R.; Piispanen, J.; Tolazzi, M. (1997). 「α-ヒドロキシカルボン酸とプロトンおよび金属イオンとの錯体の安定度定数およびそれに伴うエンタルピー変化の批判的評価。パートI：芳香族オルト-ヒドロキシカルボン酸（技術レポート）」（PDF） . Pure Appl. Chem . 69 (2): 329– 382. doi : 10.1351/pac199769020329 . S2CID 100224661 . 
52. Portanova, R; Lajunen, LHJ; Tolazzi, M.; Piispanen, J. (2003). 「プロトンおよび金属イオンとのα-ヒドロキシカルボン酸錯体の安定度定数とそれに伴うエンタルピー変化の批判的評価。第2部 脂肪族2-ヒドロキシカルボン酸（IUPAC技術報告書）」(PDF) . Pure Appl. Chem . 75 (4): 495– 540. doi : 10.1351/pac200375040495 . S2CID 97662244 . 
53. Arnaud-Neu, F.; Delgado, R.; Chaves, S. (2003). 「クラウンエーテルの金属錯体の安定度定数と熱力学関数の批判的評価（IUPAC技術報告書）」(PDF) . Pure Appl. Chem . 75 (1): 71– 102. doi : 10.1351/pac200375010071 . S2CID 97549495 . 
54. Popov, K.; Rönkkömäki, H.; Lajunen, LHJ (2001). 「ホスホン酸の安定度定数の批判的評価（IUPAC技術報告書）」(PDF) . Pure Appl. Chem . 73 (11): 1641– 1677. doi : 10.1351/pac200173101641 . S2CID 98158286 . 
55. ポポフ、K.;ロンコーマキ、H.ラジュネン、LHJ (2002)。「正誤表」（PDF）。ピュアアプリ。化学。74 (11): 2227.土井: 10.1351/pac200274112227。S2CID 195819226。 
56. Sjöberg, S. (1997). 「金属-イミダゾール系および金属-ヒスタミン系の安定度定数の批判的評価（技術報告書）」(PDF) . Pure Appl. Chem . 69 (7): 1549– 1570. doi : 10.1351/pac199769071549 . S2CID 98121760 . 
57. Berthon, G. (1995). 「極性側鎖を有するアミノ酸の金属錯体の安定度定数の批判的評価（技術報告書）」(PDF) . Pure Appl. Chem . 67 (7): 1117– 1240. doi : 10.1351/pac199567071117 . S2CID 95757342 . 
58. Smith, RM; Martell, AE; Chen, Y. (1991). 「プロトンおよび金属イオンを含むヌクレオチド錯体の安定度定数の批判的評価とそれに伴うエンタルピー変化」(PDF) . Pure Appl. Chem . 63 (7): 1015– 1080. doi : 10.1351/pac199163071015 . S2CID 97422244 . 
59. Stary, J.; Liljenzin, JO (1982). 「アセチルアセトンとその金属キレートに関する平衡定数の批判的評価」(PDF) . Pure Appl. Chem . 54 (12): 2557– 2592. doi : 10.1351/pac198254122557 . S2CID 96848983 . 
60. Beck, MT (1977). 「溶液中の平衡定数の批判的評価．金属錯体の安定度定数」（PDF） . Pure Appl. Chem . 49 (1): 127– 136. doi : 10.1351/pac197749010127 . S2CID 39693835 . 
61. Powell, Kipton, J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Sjöberg, Staffan; Wanner, Hans (2005). 「環境的に重要な重金属と無機配位子の化学的スペシエーション。パート1：Hg ²⁺ –Cl ⁻、OH ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​水性システム" (PDF) . Pure Appl. Chem . 77 (4): 739– 800. doi : 10.1351/pac200577040739 . S2CID  93650787 .
62. Powell, Kipton J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Sjöberg, Staffan; Wanner, Hans (2007). 「無機配位子による環境的に重要な金属の化学的スペシエーション パート2：Cu ²⁺ –OH ⁻、Cl ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​システム" (PDF) . Pure Appl. Chem . 79 (5): 895– 950. doi : 10.1351/pac200779050895 . S2CID  195819532 .
63. Powell, Kipton J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Leuz, Ann-Kathrin; Sjöberg, Staffan; Wanner, Hans (2009). 「無機配位子による環境的に重要な金属の化学的スペシエーション パート3：Pb ²⁺ –OH ⁻、Cl ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​システム" (PDF) . Pure Appl. Chem . 81 (12): 2425– 2476. doi : 10.1351/PAC-REP-09-03-05 . S2CID  93738375 .
64. Powell, Kipton J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Leuz, Ann-Kathrin; Sjöberg, Staffan; Wanner, Hans (2011). 「環境的に重要な金属と無機配位子の化学的スペシエーション。第4部：Cd ²⁺ –OH ⁻、Cl ⁻、CO²⁻³_​、それで²⁻⁴_​、およびPO³⁻⁴_​システム" (PDF) . Pure Appl. Chem . 83 (5): 1163– 1214. doi : 10.1351/PAC-REP-10-08-09 . S2CID  195819251 .

さらに読む

• Sigel, Roland KO; Skilandat, Miriam; Sigel, Astrid; Operschall, Bert P.; Sigel, Helmut (2013). 「第8章 カドミウムと糖残基、核酸塩基、リン酸、ヌクレオチド、核酸との錯体形成」. Sigel, Astrid; Sigel, Helmut; Sigel, Roland KO (編).カドミウム：毒性から必須元素へ(PDF) . Metal Ions in Life Sciences. 第11巻. Springer. pp.  191– 274. doi : 10.1007/978-94-007-5179-8_8 . ISBN 978-94-007-5178-1. PMID  23430775 .
• Sóvágó, Imre; Várnagy, Katalin (2013). 「第9章 アミノ酸およびペプチドのカドミウム(II)錯体」. Sigel, Astrid; Sigel, Helmut; Sigel, Roland KO (編). 『カドミウム：毒性学から必須元素へ』 . Metal Ions in Life Sciences. 第11巻. Springer. pp.  275– 302. doi : 10.1007/978-94-007-5179-8_9 . ISBN 978-94-007-5178-1. PMID  23430776 .
• ヤツィミルスキー、コンスタンチン・ボリソヴィッチ；ヴァシリエフ、ウラジミール・パブロヴィッチ（1960）『複合化合物の不安定性定数』パターソン訳、DA OUP。

外部リンク

• 安定度定数ウェブサイト: 実験滴定のためのコンピュータ プログラム、アプリケーション、データベース、およびハードウェアに関する情報が含まれています。