ユニフォームタイリング
幾何学において、ユニフォームタイリングとは、 頂点推移という制約のもと、正多角形の面によって平面をモザイク状に分割することです
均一なタイリングは、ユークリッド平面と双曲平面の両方に存在します。均一なタイリングは有限均一多面体と関連しており、球面の均一なタイリングと考えることができます。
ほとんどの一様タイリングは、対称群と基本領域内の特異生成点から始まるウィトフ構成から作成できます。平面対称群は多角形の基本領域を持ち、その群表記法、すなわち基本領域頂点の鏡映次数の列で表すことができます。
基本領域三角形は ( pqr ) と表記される。ここでp、q、rはそれぞれ 1 より大きい整数、すなわち ≥ 2 である。基本領域直角三角形は ( pq 2 ) と表記される。三角形は、 p、q、rの値に応じて、球面三角形、ユークリッド平面三角形、または双曲平面三角形のいずれかとなる。
これらの数字を表す記号体系はいくつかあります。
- 直角三角形の領域の修正されたシュレーフリ記号: ( pq 2) → { p , q }。
- コクセター・ディンキン図は、辺にp、q、rがラベル付けされた三角形グラフです。r = 2 の場合、接続数 2 の図ノードは図の枝によって互いに接続されていないため、グラフは線形です(90 度で交わるドメインミラーは新しいミラーを生成しないため)。
- ウィトフ記号は3つの整数を縦棒(|)で区切って表します。生成点が定義域頂点の鏡映点から外れている場合、その定義域頂点の鏡映次数が縦棒の前に示されます。
- 最後に、均一なタイリングは、頂点構成、つまり各(同等の)頂点の周りのポリゴンの(同一の)シーケンスによって記述できます。
全ての均一タイリングは、通常のタイリングに様々な演算を適用することで構築できます。これらの演算は、ノーマン・ジョンソンによって命名され、切り捨て(頂点の切断)、整列(辺が消えるまで頂点を切断)、カンテレーション(辺と頂点の切断)と呼ばれます。オムニトランケーションは、切り捨てとカンテレーションを組み合わせた演算です。スナッビングは、オムニトランケーションされた形状に対して交互に切り捨てを行う演算です。(詳細は、 均一多面体#ウィトフ構築演算子を参照してください。)
コクセター群
平面のコクセター群はワイトフ構成を定義し、コクセター・ディンキン図で表すことができます
整数反射順序を持つグループの場合、次のようになります。
| オービフォールド対称性 | コクセター群 | コクセター図 | 注釈 | ||
|---|---|---|---|---|---|
| コンパクト | |||||
| *333 | (3 3 3) | [3 [3] ] |    | 反射フォーム3つ、スナブ1つ | |
| *442 | (4 4 2) | [4,4] |      | 反射フォーム5個、スナブ1個 | |
| *632 | (6 3 2) | [6,3] |      | 反射フォーム7個、スナブ1個 | |
| *2222 | (∞ 2 ∞ 2) | × | [∞,2,∞] |        | 反射フォーム3つ、スナブ1つ |
| 非コンパクト(フリーズ) | |||||
| *∞∞ | (∞) | [∞] |    | ||
| *22∞ | (2 2 ∞) | × | [∞,2] |      | 鏡映形式2つ、スナブ1つ |
| オービフォールド対称性 | コクセター群 | コクセター図 | 注釈 | |
|---|---|---|---|---|
| コンパクト | ||||
| * pq 2 | ( 2ページ目) | [ p , q ] |      | 2( p + q ) < pq |
| * pqr | ( pqr ) | [( p , q , r )] |        | pq + pr + qr < pqr、すなわち1/p + 1/q + 1/r < 1 |
| パラコンパクト | ||||
| *∞ p 2 | (p∞2) | [ p ,∞] |      | p ≥ 3 |
| *∞ pq | ( pq ∞) | [( p , q ,∞)] |        | p , q ≥ 3; p + q > 6 |
| *∞∞ p | ( p ∞ ∞) | [( p ,∞,∞)] |        | p ≥ 3 |
| *∞∞∞ | (∞ ∞ ∞) | [(∞,∞,∞)] |        | |
ユークリッド平面の均一なタイリング

ユークリッド平面上には、基本三角形 (4 4 2)、(6 3 2)、(3 3 3) で構成される対称群が存在します。それぞれの対称群は、平面を基本三角形に分割する鏡映線の集合によって表されます。
これらの対称群は、3つの正則タイリングと7つの半正則タイリングを作成します。半正則タイリングの多くは、異なる対称構成子から繰り返されます。
プリズム対称群 (2 2 2 2) は、2組の平行鏡像によって表され、一般に長方形の基本領域を形成できる。新たなタイリングは生成されない。
さらに別のプリズム対称群 (∞ 2 2) は、無限基本領域を持ちます。これは、アピロゴナル・プリズムとアピロゴナル・アンチプリズムという2つの一様タイリングを構成します。
これら二つの柱状タイルの有限面を積み重ねることで、ウィソフ的ではない平面上の均一なタイルが一つ構成されます。これは正方形と三角形が交互に重なり合う、 細長い三角形タイルと呼ばれます。
直角の基本三角形: ( pq 2)
| ( 2ページ目) | ファンドの三角形 | 親会社 | 切り捨て | 修正済み | 二重切り捨て | 二重直角化(デュアル) | カンテラテッド | 全頭切断型(カンティ切断型) | スナブ |
|---|---|---|---|---|---|---|---|---|---|
| ウィトフ記号 | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| シュレーフリ記号 | { p , q } | t{ p , q } | r{ p , q } | 2t{ p , q }=t{ q , p } | 2r{ p , q }={ q , p } | rr{ p , q } | tr{ p , q } | sr{ p , q } | |
| コクセター図 |      |      |      |      |      |      |      |      | |
| 頂点構成 | p q | q .2 p .2 p | (pq)2 | p .2 q .2 q | q p | p .4. q .4 | 4.2 p .2 q | 3.3. p .3. q | |
| 正方形タイル(4 4 2) |  |  {4,4} {4,4} |  4.8.8 4.8.8 |  4.4.4.4 4.4.4.4 |  4.8.8 4.8.8 |  {4,4} {4,4} |  4.4.4.4 4.4.4.4 |  4.8.8 4.8.8 |  3.3.4.3.4 3.3.4.3.4 |
| 六角形のタイル(6 3 2) |  |  {6,3} {6,3} |  3.12.12 3.12.12 |  3.6.3.6 3.6.3.6 |  6.6.6 6.6.6 |  {3,6} {3,6} |  3.4.6.4 3.4.6.4 |  4.6.12 4.6.12 |  3.3.3.3.6 3.3.3.3.6 |
一般的な基本三角形: ( pqr )
| ウィトフ記号(pqr) | ファンドの三角形 | q | pr | rq | p | r | pq | rp | q | p | qr | pq | r | pqr | | | pqr |
|---|---|---|---|---|---|---|---|---|---|
| コクセター図 |        |        |        |        |        |        |        |        | |
| 頂点構成 | (pq)r | r .2 p.q .2 p | (広報)q | q .2 r.p .2 r | ( qr ) p | q .2 r.p .2 r | r .2 q.p .2 q | 3. r .3. q .3. p | |
| 三角形(3 3 3) |  |  (3.3) 3 (3.3) 3 |  3.6.3.6 3.6.3.6 |  (3.3) 3 (3.3) 3 |  3.6.3.6 3.6.3.6 |  (3.3) 3 (3.3) 3 |  3.6.3.6 3.6.3.6 |  6.6.6 6.6.6 |  3.3.3.3.3.3 3.3.3.3.3.3 |
非単体的基本領域
ユークリッド2次元空間において、単体ではない唯一の基本領域は、コクセター図を持つ長方形(∞ 2 ∞ 2)です





 そこから生成されるフォームはすべて正方形のタイリングになります。
そこから生成されるフォームはすべて正方形のタイリングになります。
双曲面の均一なタイリング
双曲平面上には、それぞれ異なる反射対称群 ( pqr ) に基づく凸正多角形による均一なタイリングが無数に存在します。
ここでは、ポアンカレ円板投影によるサンプリングを示します。
コクセター・ディンキン図は線形形式で表されますが、実際には三角形であり、末尾の線分rは最初のノードに接続されます。
双曲平面には、(2 2 2 3) などから始まる四辺形基本領域を持つ対称群がさらに存在し、新しい形を生成することができます。また、(∞ 2 3) など、頂点を無限遠に配置する基本領域も存在します。
直角の基本三角形: ( pq 2)
| ( 2ページ目) | ファンドの三角形 | 親会社 | 切り捨て | 修正済み | 二重切り捨て | 二重直角化(デュアル) | カンテラテッド | 全頭切断型(カンティ切断型) | スナブ |
|---|---|---|---|---|---|---|---|---|---|
| ウィトフ記号 | q | p 2 | 2 q | p | 2 | pq | 2 p | q | p | q 2 | pq | 2 | ページ2 | | |ページ2 | |
| シュレーフリ記号 | t{ p , q } | t{ p , q } | r{ p , q } | 2t{ p , q }=t{ q , p } | 2r{ p , q }={ q , p } | rr{ p , q } | tr{ p , q } | sr{ p , q } | |
| コクセター図 |      |      |      |      |      |      |      |      | |
| 頂点構成 | p q | q .2 p .2 p | pqpq | p .2 q .2 q | q p | p .4. q .4 | 4.2 p .2 q | 3.3. p .3. q | |
| (5 4 2) |  V4.8.10 V4.8.10 |  {5,4} {5,4} |  4.10.10 4.10.10 |  4.5.4.5 4.5.4.5 |  5.8.8 5.8.8 |  {4,5} {4,5} |  4.4.5.4 4.4.5.4 |  4.8.10 4.8.10 |  3.3.4.3.5 3.3.4.3.5 |
| (5 5 2) |  V4.10.10 V4.10.10 |  {5,5} {5,5} |  5.10.10 5.10.10 |  5.5.5.5 5.5.5.5 |  5.10.10 5.10.10 |  {5,5} {5,5} |  5.4.5.4 5.4.5.4 |  4.10.10 4.10.10 |  3.3.5.3.5 3.3.5.3.5 |
| (7 3 2) |  V4.6.14 V4.6.14 |  {7,3} {7,3} |  3.14.14 3.14.14 |  3.7.3.7 3.7.3.7 |  7.6.6 7.6.6 |  {3,7} {3,7} |  3.4.7.4 3.4.7.4 |  4.6.14 4.6.14 |  3.3.3.3.7 3.3.3.3.7 |
| (8 3 2) |  V4.6.16 V4.6.16 |  {8,3} {8,3} |  3.16.16 3.16.16 |  3.8.3.8 3.8.3.8 |  8.6.6 8.6.6 |  {3,8} {3,8} |  3.4.8.4 3.4.8.4 |  4.6.16 4.6.16 |  3.3.3.3.8 3.3.3.3.8 |
一般的な基本三角形: ( pqr )
| ウィトフ記号(pqr) | ファンドの三角形 | q | pr | rq | p | r | pq | rp | q | p | qr | pq | r | pqr | | | pqr |
|---|---|---|---|---|---|---|---|---|---|
| コクセター図 |        |        |        |        |        |        |        |        | |
| 頂点構成 | (広報)q | r .2 p.q .2 p | (pq)r | q .2 r.p .2 r | ( qr ) p | r .2 q.p .2 q | 2 p .2 q .2 r | 3. r .3. q .3. p | |
| (4 3 3) |  V6.6.8 V6.6.8 |  (3.4) 3 (3.4) 3 |  3.8.3.8 3.8.3.8 |  (3.4) 3 (3.4) 3 |  3.6.4.6 3.6.4.6 |  (3.3) 4 (3.3) 4 |  3.6.4.6 3.6.4.6 |  6.6.8 6.6.8 |  3.3.3.3.3.4 3.3.3.3.3.4 |
| (4 4 3) |  V6.8.8 V6.8.8 |  (3.4) 4 (3.4) 4 |  3.8.4.8 3.8.4.8 |  (4.4) 3 (4.4) 3 |  3.6.4.6 3.6.4.6 |  (3.4) 4 (3.4) 4 |  4.6.4.6 4.6.4.6 |  6.8.8 6.8.8 |  3.3.3.4.3.4 3.3.3.4.3.4 |
| (4 4 4) |  V8.8.8 V8.8.8 |  (4.4) 4 (4.4) 4 |  4.8.4.8 4.8.4.8 |  (4.4) 4 (4.4) 4 |  4.8.4.8 4.8.4.8 |  (4.4) 4 (4.4) 4 |  4.8.4.8 4.8.4.8 |  8.8.8 8.8.8 |  3.4.3.4.3.4 3.4.3.4.3.4 |
一様タイリングの拡張リスト


均一なタイリングのリストを拡張する方法はいくつかあります。
- 頂点図形は逆行面を持つことができ、頂点の周りを複数回回転することができます。
- 星型ポリゴンタイルを組み込むことができます。
- アペイロゴン、{∞}、はタイリング面として使用できます。
- ジグザグ(2 つの角度が交互に現れるアペイロゴン)も使用できます。
- タイルが端から端まで接するという制限を緩和して、ピタゴラスタイルなどの追加のタイル配置を許可することができます。
逆行する対称群の三角形には次のものがあります:
- (4/3 4/3 2)、(6 3/2 2)、(6/5 3 2)、(6 6/5 3)、(6 6 3/2)。
無限大を持つ対称群三角形には次のものが含まれます。
- (4 4/3 ∞)、(3/2 3 ∞)、(6 6/5 ∞)、(3 3/2 ∞)。
ブランコ・グリュンバウムとGCシェパードは、1987年の著書『タイリングとパターン』の第12.3節で、11種類の凸型フォームを含む25種類の均一タイリングのリストを挙げ、さらに上記の最初の2つの展開である星型多角形面と一般化頂点図形を使用して、中空タイリングと呼ぶ14種類を追加している。[ 1 ]
HSM Coxeter、MS Longuet-Higgins、JCP Millerは、1954年の論文「Uniform polyhedra」(表8:Uniform Tessellations)において、最初の3つの展開を用いて、合計38個のUniform Tilingを列挙している。2つのアペイロゴンからなるTilingも含めると、合計39個のUniform Tilingとなる。
1981年、グリュンバウム、ミラー、シェパードは論文「中空タイルを用いた均一タイリング」の中で、最初の2つの拡張を用いた25種類のタイリングと、3つ目の拡張を加えるとさらに28種類のタイリング(コクセターらの定義を用いると53種類)を挙げている。4つ目の拡張を加えると、さらに23種類の均一タイリングと10種類のファミリー(連続パラメータに基づく8種類、離散パラメータに基づく2種類)が挙げられている。[ 2 ]
11 個の凸解のほかに、共有エッジ グラフでグループ化された、Coxeterらによってリストされた 28 個の均一なスター タイリングが以下に示されます。その後に、 Coxeterらの定義を満たしているが、 Grünbaumらによって見逃された 15 個がさらにリストされます。
この集合は完全であることが証明されていません。「2.25」とは、1981年のGrünbaumらの表2の25をタイル状に並べることを意味します。
以下の3つのタイリングは、同じ面の種類が有限個しか存在しないという点で例外的です。それぞれに2つのアペイロゴンがあります。2次アペイロゴンタイリングは、2つの面が複数の辺で接するため、含まれない場合があります。
| マクニール[ 3 ] | 図 | 頂点構成 | ウィトホフ | 対称性 | 注釈 |
|---|---|---|---|---|---|
| I1 |  | ∞.∞ | p1m1 | (2つの半平面タイル、次数2のアピロゴナルタイリング) | |
| I2 |  | 4.4.∞ | ∞ 2 | 2 | p1m1 | 非等角プリズム |
| I3 |  | 3.3.3.∞ | | 2 2 ∞ | p11g | 非楕円形反プリズム |
分かりやすくするために、これ以降のタイリングは色付けされていません(重なり合うため)。1つの頂点の周りの多角形の集合が強調表示されています。マクニールはコクセターら(1954)によって示されたタイリングのみをリストしています。11個の凸一様タイリングは参考のために繰り返し示されています
| 壁紙グループの対称性 | ||||||
|---|---|---|---|---|---|---|
| マクニール[ 3 ] | グリュンバウムら、1981 [ 2 ] | エッジ図 | 強調表示 | 頂点構成 | ウィトホフ | 対称性 |
| 凸型 | 1.9 |  |  | 4.4.4.4 | 4 | 2 4 | p4m |
| I4 | 2.14 |  | 4.∞.4/3.∞ 4.∞.−4.∞ | 4/3 4 | ∞ | p4m | |
| 凸型 | 1.24 |  | 6.6.6 | 3 | 2 6 | p6m | |
| 凸型 | 1.25 |  |  | 3.3.3.3.3.3 | 6 | 2 3 | p6m |
| 15 | 2.26 |  | (3.∞.3.∞.3.∞)/2 | 3/2 | 3 ∞ | p3m1 | |
| 凸型 | 1.23 |  |  | 3.6.3.6 | 2 | 3 6 | p6m |
| I6 | 2.25 |  | 6.∞.6/5.∞ 6.∞.−6.∞ | 6/5 6 | ∞ | p6m | |
| I7 | 2.24 |  | ∞.3.∞.3/2 3.∞.−3.∞ | 3/2 3 | ∞ | p6m | |
| 凸型 | 1.14 | 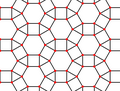 |  | 3.4.6.4 | 3 6 | 2 | p6m |
| 1 | 1.15 |  | 3/2.12.6.12 −3.12.6.12 | 3/2 6 | 6 | p6m | |
| 1.16 |  | 4.12.4/3.12/11 4.12.−4.−12 | 2 6 (3/2 6/2) | | p6m | ||
| 凸型 | 1.5 |  | 4.8.8 | 2 4 | 4 | p4m | |
| 2 | 2.7 |  |  | 4.8/3.∞.8/3 | 4 ∞ | 4/3 | p4m |
| 1.7 |  | 8/3.8.8/5.8/7 8.8/3.−8.−8/3 | 4/3 4 (4/2 ∞/2) | | p4m | ||
| 2.6 |  | 8.4/3.8.∞ -4.8.∞.8 | 4/3 ∞ | 4 | p4m | ||
| 凸型 | 1.20 |  | 3.12.12 | 2 3 | 6 | p6m | |
| 3 | 2.17 |  |  | 6.12/5.∞.12/5 | 6 ∞ | 6/5 | p6m |
| 1.21 |  | 12/5.12.12/7.12/11 12.12/5.−12.−12/5 | 6/5 6 (6/2 ∞/2) | | p6m | ||
| 2.16 |  | 12.6/5.12.∞ -6.12.∞.12 | 6/5 ∞ | 6 | p6m | ||
| 4 | 1.18 | 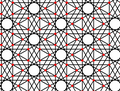 |  | 12/5.3.12/5.6/5 3.12/5.−6.12/5 | 3 6 | 6/5 | p6m |
| 1.19 |  | 12/5.4.12/7.4/3 4.12/5.-4.-12/5 | 2 6/5 (3/2 6/2) | | p6m | ||
| 1.17 |  | 4.3/2.4.6/5 3.−4.6.−4 | 3/2 6 | 2 | p6m | ||
| 5 | 2.5 | 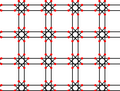 |  | 8.8/3.∞ | 4/3 4 ∞ | | p4m |
| 6 | 2.15 |  |  | 12.12/5.∞ | 6/5 6 ∞ | | p6m |
| 7 | 1.6 |  |  | 8.4/3.8/5 4.-8.8/3 | 2 4/3 4 | | p4m |
| 凸型 | 1.11 |  | 4.6.12 | 2 3 6 | | p6m | |
| 8 | 1.13 |  |  | 6.4/3.12/7 4.-6.12/5 | 2 3 6/5 | | p6m |
| 9 | 1.12 |  |  | 12.6/5.12/7 6.−12.12/5 | 3 6/5 6 | | p6m |
| 10 | 1.8 | 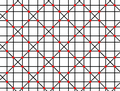 |  | 4.8/5.8/5 −4.8/3.8/3 | 2 4 | 4/3 | p4m |
| 11 | 1.22 |  |  | 12/5.12/5.3/2 -3.12/5.12/5 | 2 3 | 6/5 | p6m |
| 凸型 | 1.1 |  | 3.3.3.4.4 | 非ウィソフ派 | cmm | |
| 12 | 1.2 |  |  | 4.4.3/2.3/2.3/2 3.3.3.−4.−4 | 非ウィソフ派 | cmm |
| 凸型 | 1.3 |  | 3.3.4.3.4 | | 2 4 4 | 4ページ | |
| 13 | 1.4 |  | 4.3/2.4.3/2.3/2 3.3.−4.3.−4 | | 2 4/3 4/3 | 4ページ | |
| 14 | 2.4 |  | 3.4.3.4/3.3.∞ 3.4.3.−4.3.∞ | | 4/3 4 ∞ | 4ページ | |
| 凸型 | 1.10 |  | 3.3.3.3.6 | | 2 3 6 | p6 | |
| 2.1 |  | 3/2.∞.3/2.∞.3/2.4/3.4/3 3.4.4.3.∞.3.∞ | 非ウィソフ派 | cmm | ||
| 2.2 |  | 3/2.∞.3/2.∞.3/2.4.4 3.−4.−4.3.∞.3.∞ | 非ウィソフ派 | cmm | ||
| 2.3 |  | 3/2.∞.3/2.4.4.3/2.4/3.4/3 3.4.4.3.−4.−4.3.∞ | 非ウィソフ派 | p3 | ||
| 2.8 |  | 4.∞.4/3.8/3.8 4.8.8/3.−4.∞ | 非ウィソフ派 | p4m | ||
| 2.9 |  | 4.∞.4.8.8/3 −4.8.8/3.4.∞ | 非ウィソフ派 | p4m | ||
| 2.10 |  | 4.∞.4/3.8.4/3.8 4.8.−4.8.−4.∞ | 非ウィソフ派 | p4m | ||
| 2.11 |  | 4.∞.4/3.8.4/3.8 4.8.−4.8.−4.∞ | 非ウィソフ派 | 4ページ | ||
| 2.12 |  | 4.∞.4/3.8/3.4.8/3 4.8/3.4.8/3.−4.∞ | 非ウィソフ派 | p4m | ||
| 2.13 |  | 4.∞.4/3.8/3.4.8/3 4.8/3.4.8/3.−4.∞ | 非ウィソフ派 | 4ページ | ||
| 2.18 |  | 3/2.∞.3/2.4/3.4/3.3/2.4/3.4/3 3.4.4.3.4.4.3.∞ | 非ウィソフ派 | p6m | ||
| 2.19 |  | 3/2.∞.3/2.4.4.3/2.4.4 3.−4.−4.3.-4.−4.3.∞ | 非ウィソフ派 | p6m | ||
| 2.20 |  | 3/2.∞.3/2.∞.3/2.12/11.6.12/11 3.12.−6.12.3.∞.3.∞ | 非ウィソフ派 | p6m | ||
| 2.21 |  | 3/2.∞.3/2.∞.3/2.12.6/5.12 3.−12.6.−12.3.∞.3.∞ | 非ウィソフ派 | p6m | ||
| 2.22 |  | 3/2.∞.3/2.∞.3/2.12/7.6/5.12/7 3.12/5.6.12/5.3.∞.3.∞ | 非ウィソフ派 | p6m | ||
| 2.23 |  | 3/2.∞.3/2.∞.3/2.12/5.6.12/5 3.−12/5.−6.−12/5.3.∞.3.∞ | 非ウィソフ派 | p6m | ||
頂点配置4.8.−4.8.−4.∞には2つの均一タイリングがあり(Grünbaum et al.、2.10および2.11)、頂点配置4.8/3.4.8/3.−4.∞にも2つの均一タイリングがあり(Grünbaum et al. 、2.12および2.13)、それぞれ対称性が異なります。また、各頂点配置には、擬似均一(頂点が2つの対称軌道をとる)の3つ目のタイリングもあります。これらは異なる正方形の面のセットを使用します。したがって、星型ユークリッドタイリングでは、頂点配置が必ずしもタイリングを決定するわけではありません。[ 2 ]
下の図では、水平方向と垂直方向の辺を持つ正方形が中央の点で示されています。また、単一の正方形の辺はハイライト表示されています。[ 2 ]
- 2.10と2.12 (p4m)
- 2.11と2.13 (p4g)
- 擬似一様
ジグザグのタイリングを以下に示します。{∞ 𝛼 } は、角度 0 < 𝛼 < π のジグザグを表します。アペイロゴンは、𝛼 = π の特別な場合と考えることができます。対称性は一般的なケースに対して与えられていますが、𝛼 の特別な値によって対称性が増す場合があります。タイリング 3.1 と 3.12 は正規化することさえあります。3.32 はすでに正規化されています(自由パラメータがありません)。タイリングを退化させるような𝛼 の特別な値が存在する場合もあります。[ 2 ]
| ジグザグ模様のタイル | |||
|---|---|---|---|
| グリュンバウムら、1981 [ 2 ] | 図 | 頂点構成 | 対称性 |
| 3.1 |  | ∞ 𝛼 .∞ β .∞ γ 𝛼+β+γ=2π | p2 |
| 3.2 |  | ∞ 𝛼 .∞ β .−∞ 𝛼+β 0<𝛼+β≤π | p2 |
| 3.3 |  | 3.3.∞ π−𝛼 .−3.∞ 𝛼+2π/3 0≤𝛼≤π/6 | pgg |
| 3.4 |  | 3.3.−∞ π−𝛼 .−3.∞ −𝛼+2π/3 0≤𝛼<π/3 | pgg |
| 3.5 |  | 4.4.∞ φ .4.4.−∞ φ φ=2 arctan( n / k )、nk は偶数、( n , k )=1 φ=2 arctan 2 について描かれる | pmg |
| 3.6 |  | 4.4.∞ φ .−4.−4.∞ φ φ=2 arctan( n / k )、nk は偶数、( n , k )=1 φ=2 arctan 1/2 について描かれる | pmg |
| 3.7 |  | 3.4.4.3.−∞ 2π/3 .−3.−∞ 2π/3 | cmm |
| 3.8 |  | 3.−4.−4.3.−∞ 2π/3 .−3.−∞ 2π/3 | cmm |
| 3.9 |  | 4.4.∞π /3 .∞.−∞π /3 | p2 |
| 3.10 |  | 4.4.∞ 2π/3 .∞.−∞ 2π/3 | p2 |
| 3.11 |  | ∞.∞ 𝛼 .∞.∞ −𝛼 0<𝛼<π | cmm |
| 3.12 |  | ∞ 𝛼 .∞ π−𝛼 .∞ 𝛼 .∞ π−𝛼 0<𝛼≤π/2 | cmm |
| 3.13 |  | 3.∞ 𝛼 .−3.−∞ 𝛼 π/3<𝛼<π | p31m |
| 3.14 |  | 4.4.∞ 2π/3 .4.4.−∞ 2π/3 | p31m |
| 3.15 |  | 4.4.∞ π/3 .−4.−4.−∞ π/3 | p31m |
| 3.16 |  | 4.∞ 𝛼 .−4.−∞ 𝛼 0<𝛼<π, 𝛼≠π/2 | 4ページ |
| 3.17 |  | 4.−8.∞ π/2 .∞.−∞ π/2 .−8 | cmm |
| 3.18 |  | 4.−8.∞ π/2 .∞.−∞ π/2 .−8 | 4ページ |
| 3.19 |  | 4.8/3.∞ π/2 .∞.−∞ π/2 .8/3 | cmm |
| 3.20 |  | 4.8/3.∞ π/2 .∞.−∞ π/2 .8/3 | 4ページ |
| 3.21 |  | 6.−12.∞ π/3 .∞.−∞ π/3 .−12 | p6 |
| 3.22 |  | 6.−12.∞ 2π/3 .∞.−∞ 2π/3 .−12 | p6 |
| 3.23 |  | 6.12/5.∞π / 3.∞.−∞π / 3.12/5 | p6 |
| 3.24 |  | 6.12/5.∞ 2π/ 3.∞.−∞ 2π/ 3.12/5 | p6 |
| 3.25 |  | 3.3.3.∞ 2π/3 .−3.∞ 2π/3 | p31m |
| 3.26 |  | 3.∞.3.−∞ 2π/3 .−3.−∞ 2π/3 | cm |
| 3.27 |  | 3.∞.−∞ 2π/3.∞. −∞ 2π/ 3.∞ | p31m |
| 3.28 |  | 3.∞ 2π/3 .∞ 2π/3 .−3.−∞ 2π/3 .−∞ 2π/3 | p31m |
| 3.29 |  | ∞.∞ π/3 .∞ π/3 .∞.−∞ π/3 .−∞ π/3 | cmm |
| 3.30 |  | ∞.∞ π/3 .−∞ 2π/3 .∞.∞ 2π/3 .−∞ π/3 | p2 |
| 3.31 |  | ∞.∞ 2π/3 .∞ 2π/3 .∞.−∞ 2π/3 .−∞ 2π/3 | cmm |
| 3.32 |  | ∞ π/3 .∞ π/3 .∞ π/3 .∞ π/3 .∞ π/3 .∞ π/3 | p6m |
| 3.33 |  | ∞ π/3 .−∞ 2π/3 .−∞ 2π/3 .− ∞ π/3 .−∞ 2π/3 .−∞ 2π/3 | cmm |
タイリングペア3.17と3.18、および3.19と3.20は、頂点構成は同じですが、対称性が異なります。[ 2 ]
タイル3.7から3.10は2.1と2.2と同じエッジ配置を持ち、3.17から3.20は2.10から2.13と同じエッジ配置を持ち、3.21から3.24は2.18から2.23と同じエッジ配置を持ち、3.25から3.33は1.25(正三角形のタイル)と同じエッジ配置を持ちます。[ 2 ]
自己双対タイリング
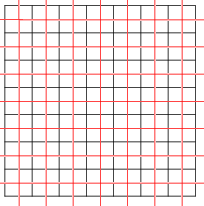
タイリングは自己双対になることもあります。シュレーフリ記号{4,4}で表される正方形タイリングは自己双対です。ここに示されているのは、互いに双対な2つの正方形タイリング(赤と黒)です。
非凸等角単純多角形として正多角形または等角多角形を使用した均一タイリング

正星型多角形を、 2 倍の (短い) 辺を持ち、同じ外角と「内側」の内角が交互になっている非凸型等倍単純多角形として見ると、正星型多角形をタイリングに使用できます。また、等倍単純多角形を「正多角形」として見ると、正星型多角形を「均一な」タイリングに使用できます (ただし、すべてが使用できるわけではありません)。
また、特定の非正規の等倍星型多角形のアウトラインは、同じ数の(短い)辺を持ち、同じ外角と「内側」の内角が交互になった非凸等倍(単純)多角形です。この種類の等倍星型多角形をアウトラインとして見ると、タイリングに使用できます。また、等倍単純多角形を「正規」と見なすと、この種類の等倍星型多角形を「均一」なタイリングに使用できます(ただし、すべてが使用できるわけではありません)。
外角 𝛼 を持つ等角単純2 n角形は { n 𝛼 } と表記され、その外頂点はnと表記される。* 𝛼、内側のものはnとして** 𝛼。
タイリングの定義を拡張するには、2つのポリゴンしかないコーナーを頂点と見なさないことが必要です。少なくとも3つのポリゴンを持つ頂点の頂点構成は、そのような「均一な」タイリングを定義するのに十分であり、後者は1つの頂点構成を持つことになります(そうでなければ2つになります)。調整可能な角度𝛼を持つこのような均一なタイリングは4つあり、特定の角度でのみ機能するこのような均一なタイリングは18つあり、合計22の星型ポリゴンを使用する均一なタイリングになります。[ 4 ]
これらすべてのタイリングは、可能性のある 2 次頂点が無視され、可能性のある二重エッジと三重エッジが単一エッジに削減され、通常の均一タイリング (凸正多角形のみを使用) と位相的に関連しています。
 3.6* 𝛼.6** 𝛼3.12.12に関連するトポル 3.6* 𝛼.6** 𝛼3.12.12に関連するトポル |  4.4* 𝛼.4** 𝛼4.8.8に関連するトポル 4.4* 𝛼.4** 𝛼4.8.8に関連するトポル |  6.3* 𝛼.3** 𝛼トポル。6.6.6に関連 6.3* 𝛼.3** 𝛼トポル。6.6.6に関連 |  3.3* 𝛼3.3** 𝛼3.6.3.6に関連するトポル 3.3* 𝛼3.3** 𝛼3.6.3.6に関連するトポル |
 4.6.4* π/64.4.4.4に関連する6つの位相 4.6.4* π/64.4.4.4に関連する6つの位相 |  (8.4* π/4)2トポル。4.4.4.4に関連する (8.4* π/4)2トポル。4.4.4.4に関連する |  12.12.4* π/34.8.8に関連するトポル 12.12.4* π/34.8.8に関連するトポル |  3.3.8* π/12.4** π/3.8* π/124.8.8に関連するトポル 3.3.8* π/12.4** π/3.8* π/124.8.8に関連するトポル |  3.3.8* π/12.3.4.3.8* π/124.8.8に関連するトポル 3.3.8* π/12.3.4.3.8* π/124.8.8に関連するトポル |  3.4.8.3.8* π/124.8.8に関連するトポル 3.4.8.3.8* π/124.8.8に関連するトポル |
 5.5.4* π/10.5.4* π/103.3.4.3.4に関連する位相幾何学 5.5.4* π/10.5.4* π/103.3.4.3.4に関連する位相幾何学 |  4.6* π/6.6** π/2.6* π/6トポル。6.6.6に関連 4.6* π/6.6** π/2.6* π/6トポル。6.6.6に関連 |  (4.6* π/6) 3位相幾何学は6.6.6と関連している (4.6* π/6) 3位相幾何学は6.6.6と関連している |  9.9.6* 4π/9トポル。6.6.6に関連 9.9.6* 4π/9トポル。6.6.6に関連 |  (6.6* π/3) 2位相幾何学は3.6.3.6と関連している (6.6* π/3) 2位相幾何学は3.6.3.6と関連している |  (12.3* π/6) 2位相幾何学は3.6.3.6と関連している (12.3* π/6) 2位相幾何学は3.6.3.6と関連している |
 3.4.6.3.12* π/64.6.12に関連するトポル 3.4.6.3.12* π/64.6.12に関連するトポル |  3.3.3.12* π/6.3.3.12* π/63.12.12に関連するトポル 3.3.3.12* π/6.3.3.12* π/63.12.12に関連するトポル |  18.18.3* 2π/93.12.12に関連するトポル 18.18.3* 2π/93.12.12に関連するトポル |  3.6.6* π/33.4.6.4に関連する6つのトポル 3.6.6* π/33.4.6.4に関連する6つのトポル |  8.3* π/128.6* 5π/12トポル。3.4.6.4に関連 8.3* π/128.6* 5π/12トポル。3.4.6.4に関連 |  9.3.9.3* π/93.6.3.6に関連するトポル 9.3.9.3* π/93.6.3.6に関連するトポル |
凸等倍単純多角形を用いた一様タイリング
非正則等角多角形(星型または単純2 n角形)は、常に2つの角が交互に配置されます。等角多角形(単純2 n 角形、{n𝛼 })は凸多角形になる可能性があり、最も単純なものは菱形(2×2角形、{2𝛼 } )です。これらの凸多角形({ n𝛼 })を「正則」多角形と見なすことで、より多くのタイリングを「均一」と見なすことができます。
 3.2* π/3.6.2** π/3トポル。3.4.6.4に関連 3.2* π/3.6.2** π/3トポル。3.4.6.4に関連 |  4.4.4.4トポル( 4.4.4.4に関連) 4.4.4.4トポル( 4.4.4.4に関連) |  (2* π/4.2** π/4)2トポル。4.4.4.4に関連する (2* π/4.2** π/4)2トポル。4.4.4.4に関連する |  2* π/4.2* π/4.2** π/4.2** π/44.4.4.4に関連するトポル 2* π/4.2* π/4.2** π/4.2** π/44.4.4.4に関連するトポル |  4.2* π/44.2** π/44.4.4.4に関連するトポル 4.2* π/44.2** π/44.4.4.4に関連するトポル |
参照
参考文献
- ^『タイルとパターン』、表12.3.1、640ページ
- ^ a b c d e f g hブランコ・グリュンバウム; ミラー JCP; シェパード GC (1981). 「中空タイルを用いた均一なタイリング」. チャンドラー・デイビス; ブランコ・グリュンバウム; FA・シェルク (編). 『幾何学的鉱脈:コクセター記念論文集』. シュプリンガー. pp. 17– 64. ISBN 978-1-4612-5650-2。
- ^ a bジム・マクニール
- ^ Tilings and Patterns、Branko Gruenbaum、GC Shephard、1987年、2.5「スターポリゴンを使用したタイリング」、pp. 82–85。
- ノーマン・ジョンソン『均一多面体』、原稿(1991年)
- NWジョンソン:均一多面体とハニカムの理論、博士論文、トロント大学、1966年
- グリュンバウム、ブランコ、シェパード、GC (1987). 『タイルとパターン』 WHフリーマン・アンド・カンパニー. ISBN 0-7167-1193-1。(星型タイリング セクション12.3)
- HSM Coxeter、MS Longuet-Higgins、JCP Miller、「均一多面体」、Phil. Trans.、1954、246 A、401–50 JSTOR 91532(表8)
外部リンク
- ワイスタイン、エリック・W. 「均一テッセレーション」MathWorld
- ユークリッド平面上の均一なテッセレーション
- 平面のモザイク模様
- デイヴィッド・ベイリーのテッセレーションの世界
- k均一タイリング
- n均一なタイリング
- Klitzing, Richard. 「4D ユークリッド タイル」
| スペース | ファミリー | / / | ||||
|---|---|---|---|---|---|---|
| E 2 | ユニフォームタイリング | 0 [3] | δ 3 | hδ 3 | qδ 3 | 六角形 |
| E 3 | 均一な凸型ハニカム | 0 [4] | δ 4 | hδ 4 | qδ 4 | |
| E 4 | 均一4セルハニカム | 0 [5] | δ 5 | hδ 5 | qδ 5 | 24セルハニカム |
| E 5 | 均一5セルハニカム | 0 [6] | δ 6 | hδ 6 | qδ 6 | |
| E 6 | 均一6ハニカム | 0 [7] | δ 7 | hδ 7 | qδ 7 | 2 22 |
| E 7 | 均一7ハニカム | 0 [8] | δ 8 | hδ 8 | qδ 8 | 1 33 • 3 31 |
| E 8 | 均一8ハニカム | 0 [9] | δ 9 | hδ 9 | qδ 9 | 1 52 • 2 51 • 5 21 |
| E 9 | 均一9ハニカム | 0 [10] | δ 10 | hδ 10 | qδ 10 | |
| E 10 | 均一な10ハニカム | 0 [11] | δ 11 | hδ 11 | qδ 11 | |
| E n −1 | 均一な(n −1)ハニカム | 0 [ n ] | δ n | hδ n | qδ n | 1 k 2 • 2 k 1 • k 21 |













